平面空间划分对建筑自然通风性能影响的研究*

宋修教，张 悦，程晓喜，黄献明，连 璐，贺秋时，林奕莹

引言

优良的建筑自然通风有利于室内污浊气体与室外新鲜空气的置换，有利于过热季节的通风降温，进而提升人的体感舒适度，增进人与自然的融入感。近年来，随着“经济、适用、绿色、美观”八字建设方针、“双碳”目标的提出和两办联合印发《关于推动城乡建设绿色发展的意见》1），建筑行业的“绿色”也越来越受到重视。如何回归以建筑设计、而非全靠设备技术的手段改善室内自然通风条件成为一个研究热点。从建筑师做方案设计的流程来看，建筑的场地布局、组合方式、外观形态、室内划分等环节均可对建筑的室内外风环境产生影响，而平面划分对室内风环境的影响最为直接。

1 国内外研究趋势综述与本研究定位

1.1 室内通风与内部空间分隔的相关研究聚焦于中庭

既往有关建筑室内空间设计与自然通风性能的研究多集中在影响热压通风的中庭研究如单中庭形态、多中庭组合、中庭与边庭结合应用、中庭进出风口尺度等。如肖毅强等研究了湿热地区有利通风的中庭侧庭组合方式、进出风口大小和位置对自然通风降温效果的影响[1]，邓孟仁等研究了超高层塔楼的腔体高度、进出风口大小和位置对室内热环境的影响[2]，李浩达研究了有利于中庭自然通风的平面剖面形态及组合方式[3]，Andrew Acred等研究了多层建筑的中庭烟囱通风的一种无量纲设计方法[4]。但对影响风压通风的标准层平面空间划分要素如平面选型、平面组织方式及墙体分隔疏密程度等研究不足。

本研究选取高层办公楼的单一标准层平面为研究对象，过滤掉中庭热压拔风的影响，构建了内部平面规律变化的模型矩阵，观察风压驱动下平面分隔对室内通风的影响。

1.2 室内通风与平面分隔的相关研究不足

已有的有关平面分隔影响通风的研究，多为建环科学家对住宅既有平面方案的优化调整或对简化模型的精确模拟，建筑学领域的研究较少、且多为对平面分隔的模式类型化归纳。如张雪琳研究比较了采用几个小短墙替代一个总长度一致的较长墙对风压通风的不同影响[5]，此研究搭建了理想化的单房间模型来开展，结论精确但对指导建筑设计意义不大。李晓东[6]按照《建筑空间组合论》[7]中对公共建筑布局手法的论述，将“一”字型平面分为单廊式、双廊式两种模式分别模拟、比较结果，抓住了平面组织模式这一风压驱动下的关键因子，但忽视了同一平面组织模式下墙体划分疏密度的影响。

本研究尝试采用内墙分隔疏密度2）规律变化的标准层平面模型来模拟，以期得到平面分隔度影响室内通风的更细致描述。

1.3 外窗开启洞口与平面分隔对通风性能的协同影响研究缺失

外窗洞口作为气流传导的关键路径，相关研究较为丰富，主要研究对象为开窗面积、开窗位置、开窗方式、开窗角度、开启时段等。如Arka A M等在其对房间通风模拟建模中关注了外窗可开启扇洞口与外墙面积比这个要素[8]，Melaragno研究了开窗位置对房间内空气流动路线的影响[9]，刘庆分析了推拉窗这一开窗方式的有效面积折算和阻力特性[10]，Givoni研究发现垂直于主导风向变化45°不会明显减少通风效果[11]，朱新荣等分析了夜间通风建筑的关键设计参数、进行了灵敏度和匹配关系研究[12]。但有关外窗开启扇变化与标准层平面分隔变化同时作用于室内通风的研究目前还几乎处于空白。风压驱动下的平面通风是一个由外窗流入、经由室内墙体分隔的房间、穿过门洞、由另一侧外窗流出的连续过程，门窗洞口的设置对研究标准层室内墙体分隔的建模影响较大。

本研究将每一个标准层模型都置于不同外窗开启扇洞口面积比3）下进行了模拟，以期观察窗洞比与分隔度对室内自然通风的协同影响。

1.4 本研究定位

综上，本研究从建筑师控制形体空间的视角出发，设计分隔度规律变化的标准层模型矩阵，观察模型矩阵在不同窗洞比下的自然通风表现。以期得到分隔度对室内通风的影响规律，及这一规律在不同窗洞比下的具体呈现。

2 平面分隔建模设计与风环境模拟评价参数选择

2.1 建筑师视角下的平面分隔模型设计

本研究尝试建立基于建筑师视角下的平面分隔模型矩阵。笔者对近年来建筑师参与较多的绿色公共建筑项目进行了调研，对《建筑设计资料集（第三版）第3分册 办公·金融·司法·广电·邮政》[13]中的办公建筑、教学建筑等平面进行了归纳，尝试构建一组标准层面积相同的模型矩阵。以不同进深、不同分隔度、不同窗洞比的标准层模型作为风环境模拟的研究对象，观察各平面模型的通风性能表现。

控制各固定条件为：标准层面积为2500m24）、[14]63，使用系数5）为0.75，则实用面积约为1875m2；柱跨为9m，面宽均为奇数跨6）；建筑高度为50m7）、[14]57，首层层高4.8m，标准层层高4.2m，共计11层，屋顶设备层3.2m。

各可变条件为：（1）建筑进深。依据案例归纳为图1自上至下的5组，变化规律为进深依次增大，分别为2跨、3跨、4跨、5跨。根据对资料集相关案例的归纳，各进深平面的核心筒布置模式依次呈现为多核心筒沿面宽依次布置、双核心筒分置两端、扁长单核心筒居中、方形单核心筒居中（或多核心筒分散至四角）。（2）分隔度。依据案例归纳为图 1自左至右的4列，分别基于开敞办公、大开间办公、较大房间办公、小隔间办公4种办公室划分模式构建分隔度的变化颗粒度。（3）窗洞比。依据各设计规范中对外窗开启扇的相关规定及设计经验，控制窗洞比依次为1%8）、[15]、2%9）、[16]、3.5%10）、5%11）、[17]、8%12）、[18]。

图1 进深不同、室内平面分隔度连续变化的标准层平面模型矩阵

2.2 风环境模拟条件设置及指标评价

在算法及软件选取上，选用绿色建筑风环境模拟分析软件PKPM-CFD（V3.2）的室内风模块。该软件为基于英国OPENFOAM内核二次开发的国产软件，实现了基于AUTOCAD开发的国产插件天正T20等各版本所建模型的一键导入、识别，相比传统风模拟软件建模效率有所提高。软件开发团队委托第三方搭建风洞试验模型，将实测结果与同一模型在PKPM-CFD软件的模拟结果相比对，得到综合平均误差为10.18%，准确性良好13）。

在边界条件（初始风况）参数上，因文献[19]已论证建筑朝向或风来向对通风性能影响不明显，本研究忽略朝向因素，所有模型选取与标准层平面面宽向呈45°夹角的方向为初始风向；根据《中国建筑热环境分析专用气象数据集》[20]中对我国四个典型气候区代表城市哈尔滨、北京、上海、深圳的典型年的过渡季—夏季逐时风速统计，选取3m/s作为初始风速。所用湍流模型、计算算法为标准κ-ε模型14）。

在研究对象选取上，在控制模拟工作量可接受的范围内选取进深变化最具代表性的图 1中A1～A4、C1～C4、D1～D4，这3组为模拟对象；每个模型均分别按5种窗洞比模拟，共进行60次模拟。

在模拟参数设置上，主要依据为《民用绿色建筑性能计算标准JGJ/T449-2018》[21]。模型高度为标准层层高4.2m，计算域设置为标准层平面尺寸的3倍，在63m至357m之间波动，满足标准要求的“流入端距离5H，流出端距离10H”；网格设定过小会延长计算时间，过大则不够精确，因本模型中所有构件的最小尺寸为墙体厚度200mm，设定最小网格尺寸为200mm，即可识别所有构件；设定最大网格为800mm，背景网格尺寸为2400mm，网格过渡比为1.3，于模型元素密集处自动加密，总网格数在100万左右，满足规范要求的“形状规整的建筑网格过渡比不宜大于1.5”。设定收敛精度为0.0001，迭代步数为500次，计算达到收敛即停止，在保证精确度同时控制模拟时间在可接受范围内。在评价指标上，主要参考《绿色建筑评价标准GB/T 50378-2019》[15]12，当中对室内通风性能的相关要求为“公共建筑在过渡季典型工况下主要功能房间平均自然通风换气次数不小于2次/h的面积比例达到70%，得5分，每再增加10%，多得1分，最高得8分”。可见，对单个房间，换气次数15）、[22，23]为重要评价指标。

通常可定义“标准层平均换气次数”为评估标准层内所有房间的通风性能优劣的指标，为“单位时间内标准层的所有房间通风量之和与标准层体积之比×100%”，单位为“次/小时”。计算公式为：标准层平均换气次数n= 所有房间的通风量之和/ 标准层各房间体积之和×100% 。

但这一指标有缺陷，本研究尝试提出“标准层新风换气次数”为评价指标（以下正文简称“换气次数”）。传统的换气次数概念中，非迎风侧房间所统计的“通风量”绝大部分为从迎风侧房间（或经由走廊等空间）流入的重复统计结果。室外新风流经室内后，其通风降温效果、改善空气质量的能力均下降，笼统地将这部分通风量计入其中，并不能准确表征标准层整体的通风性能优劣。因而本研究尝试提出“标准层新风换气次数”为评价指标，定义为“单位时间内标准层的所有房间新风量之和与标准层体积之比”，单位为“次/小时”，此处“所有房间新风量之和”即迎风侧房间通风量之和。标准层新风换气次数的计算公式为：标准层新风换气次数N= 迎风侧房间的通风量之和/ 标准层各房间体积之×100% 。

3 模拟结果与数据分析

3.1 风速云图及数值观察

经软件模拟，得到如表1、表2、表316）三组结果。三个表分别呈现长条状板楼标准层平面、矩形塔楼标准层平面、方形塔楼标准层平面在不同分隔度、不同窗洞比下的换气次数及风速云图。呈现如下特征：

表1 长条状板楼标准层平面（A1～A4）在不同内墙分隔疏密度下的新风换气次数及风速云图统计表

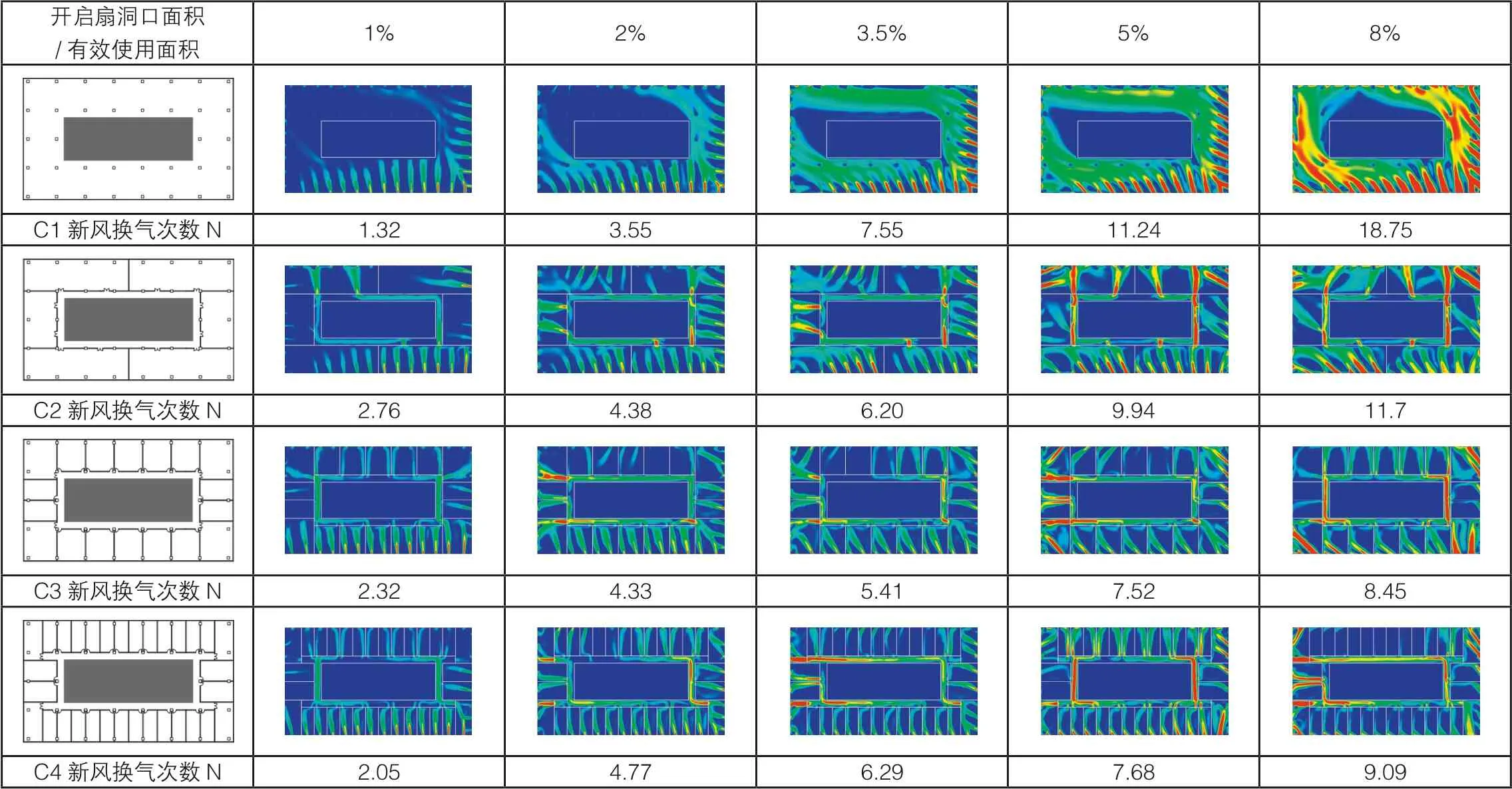
表2 矩形塔楼标准层平面（C1～C4）在不同内墙分隔疏密度下的新风换气次数及风速云图统计表

表3 方形塔楼标准层平面（D1～D4）在不同内墙分隔疏密度下的新风换气次数及风速云图统计表

（1）内走廊处呈现高亮，这表明内走廊风速较其它房间风速大。分析其原因为，内走廊不临外窗，流经内走廊的风量均为迎风侧房间流入，流出至背风侧房间。内走廊的风流量与迎风侧房间、背风侧房间均等，但其总体积远小于迎风侧房间、背风侧房间且为窄长条空间，因而风在内走廊处快速通过，风速大。

（2）各房间外窗开启扇洞口处至门洞处呈现高亮但周围区域亮度低，这表明各房间风速分布不均、门窗洞口连线区域风速快但其余区域风速低。分析其原因为，模拟中将各模型的门窗开启扇简化为洞口，缺少了风流入、流出两端的干扰；建模过程中省略了房间内家具布置、人员分布等对风流经房间的干扰。

（3）从左至右观察各行5个云图及数值，随着窗洞比递增，云图逐个变亮、数值逐个增大，这点与常识相符。

（4）从上到下观察各列4个云图及数值，随着分隔度递增，云图及数值皆未均匀变化，而是表现为有隔墙的3个相近、无隔墙的1个区别大。对比风速云图，无隔墙平面相较有隔墙平面风速更均匀、风向更稳定，这表明隔墙对室内风场的影响较大。分析其原因为，对无隔墙平面而言，间隔均质的水平长窗开启扇可近似看作水平线形进风口、出风口，气流分布均匀、稳定，亮部图像呈现由风来向到对向的连续面；对有隔墙平面特别是小隔间平面而言，单个开启扇和门洞近似作为点式进风口、出风口，气流分布受门窗位置影响较大，亮部图像呈现为各房间连接进风口到出风口的多条线。对比换气次数的数值，亦呈现有无隔墙的区别，具体在3.4讨论。

3.2 标准层新风换气次数随进深增大而降低

观察窗洞比、分隔度都不变情况下，换气次数随进深变化的趋势：分别比较3个表的同一位置的3个数据换气次数的变化，例如3个表左上角的数值分别为1.69次/时、1.32次/时、1.25次/时，数值依次变小；同样地，分别比较其余15个位置的数值，结果均依次变小。

以上比较方法细致但较繁琐。选取3个表的同一列上4个数值求平均值，以表征在过滤掉分隔度的干扰时，同一窗洞比下进深对换气次数的影响，如图 2所示，5条折线均呈现换气次数随进深增大而减小的趋势。

由此可见，进深对换气次数影响明显；标准层进深越小，换气次数越大，自然通风换气性能越好。

3.3 标准层新风换气次数随外窗开启扇洞口面积比增大而增加

窗洞比对换气次数影响明显。如图 2所示，在过滤掉分隔度的干扰时，窗洞比较大的折线位于窗洞比较小的折线之上，表明窗洞比大的标准层换气次数大于窗洞比小的标准层。

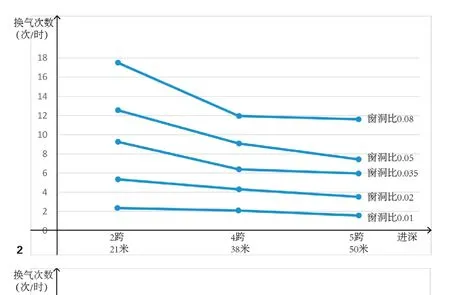
图2 不同窗洞比下换气次数随进深变化折线图

由此可见，窗洞比对换气次数影响明显；窗洞比越大，换气次数越大，自然通风换气性能越好。

3.4 标准层新风换气次数与内墙分隔疏密度无关，与有无分隔相关、且以2.5%的外窗开启扇洞口面积比为临界点呈差异化表现

观察三个表的纵向共15列数值以分析分隔度变化对换气次数的影响。以表 2的5列数值为例，每一列数值代表同一标准层在同一窗洞比下随分隔度变化的换气次数，自上而下分隔度递增。可得到以下规律：

规律一，C1与C2～417）结果有较大差值而C2～4三个数值差异较小，表 1、表 3的另10列数据亦呈现此规律18）。这表明室内有无分隔对换气次数影响明显，而分隔度变化对换气次数影响不明显19）。

规律二，窗洞比为1%时C2～4的数值明显高于C1，窗洞比为2%时C2～4的数值略高于C1，窗洞比为3.5%时C2～4的数值略低于C1，窗洞比为5%、8%时C2～4的数值明显低于C1。可看到，随着窗洞比递增，两组数值呈现大小关系的转变，且存在一个窗洞比值是分隔度影响换气次数规律的变化临界点，观察表 1表 3的另10列数据亦呈现此规律。为探寻临界点数值，绘制换气次数随窗洞比渐变的折线图，如图 3所示，可得此临界值约为2.5%，且不随进深变化而变动。

综上，可得结论：（1）同一内部空间组织模式下，标准层的分隔度变化对换气次数影响不明显。（2）标准层内有无分隔对换气次数影响明显，且以窗洞比2.5%为临界值，呈现差异化表现：当窗洞比小于2.5%时，有分隔的换气次数大于无分隔；当窗洞比大于2.5%时，有分隔的换气次数小于无分隔；当窗洞比为2.5%时，有无分隔的换气次数趋近。

4 结论与设计策略

本研究通过构建分隔度精细变化的标准层模型矩阵，综合考虑窗洞比的影响，得出如下结论：

（1）控制进深不要过大，有利于改善自然通风换气性能

当建筑为单廊或双廊的条状体量、进深控制在20m之内，有利于通风换气；当建筑为厚板楼或扁长矩形平面、进深在20m至40m之间，可通过调节门窗开启状态来进一步改善通风换气；当建筑为进深大于40m的塔楼或超大体量，可设置的外窗开启扇受限于外部大风，内区需增加机械通风以保证换气效果。

（2）控制窗洞比不要过小，有利于改善自然通风换气性能

当窗洞比为2.5%时，建筑在门窗全开状态下可保证不低于4次/ h的平均换气次数，保洁人员保持每小时门窗全开15min即可使室内换气1次。

依据窗洞比定义，以本文2.1中的标准层面积2500m2、使用效率0.75的典型高层办公楼为例，窗洞比2.5%折算得总开启面积约为46m2。外窗为连续水平长窗的情况下，大约每隔4～6扇窗开启1扇平开窗、或2扇悬窗即可。

（3）平面分隔度对自然通风换气性能影响不明显，有无平面分隔影响明显

当窗洞比小于2.5%时，有平面分隔的隔间设计有利通风；当窗洞比为2.5%时，有无平面分隔对通风性能影响不明显；当窗洞比大于2.5%时，无平面分隔的开敞办公有利通风，但应注意防止过量通风。

致谢：衷心感谢支撑本文的基金项目负责人崔愷院士对本研究的关心、《南方建筑》杂志审稿专家对本文的指正、中国建研院北京构力科技有限公司（PKPM）绿色低碳软件事业部产品总监刘剑涛对本文所用工具的支持及指导！

图、表来源

本文图、表均由宋修教绘制。

注释

1）2015年12月召开的中央城市工作会议正式发布了“适用、经济、绿色、美观” 的国家新时期建筑方针；2020年9月22日，中国政府在第七十五届联合国大会上提出：“中国将提高国家自主贡献力度，采取更加有力的政策和措施，二氧化碳排放力争于2030年前达到峰值，努力争取2060年前实现碳中和”；2021年10月21日，中共中央办公厅、国务院办公厅印发《关于推动城乡建设绿色发展的意见》。

2）本文定义“室内墙体分隔疏密度”，以表征在特定标准层平面轮廓中用作划分房间的墙体分布疏密程度，计算方法为“内隔墙总长度/标准层实用地板面积*100%”，无量纲。以下正文简称“分隔度”。

3）本文定义“外窗开启洞口面积比”，以表征在特定标准层中用作自然通风的外窗可开启扇折算之后的有效面积占外立面面积比例，计算方法为“开启有效面积/标准层外立面面积*100%”，无量纲。以下正文简称“窗洞比”。

4）据2018年新版《建筑设计防火规范GB50016-2014》第63、64页表5.3.1，“一、二级高层民用建筑防火分区最大允许建筑面积为1500㎡”，据表注1，“当建筑内设置自动灭火系统时，可按表中规定增加1倍”，即上限为3000㎡。据第63页5.2.4，“当建筑物的占地面积总和不大于2500㎡时，可成组布置”。出于规范限制及设计灵活性，通常标准层面积控制在2500㎡及以下。5）使用系数，即为标准层平面中去除走廊、楼电梯、厕所、设备间等公用空间之后的剩余空间与标准层面积的比值。一般为0.72到0.85之间。

6）据设计经验，柱跨为9m或8.4m有利于标准层正投影下方地下车位的排布，因高层建筑结构所需柱径较大，通常选取9m为柱跨尺寸；标准层面宽为奇数跨，面宽中部无柱，有利于组织空间。7）通常建筑高度越大，各项建设条件的限制越严苛。例如《建筑设计防火规范GB50016-2014》第57页表5.1.1，“建筑高度大于50m的公共建筑为一类建筑”，相应的防火要求须按一类建筑实施。出于土地利用效率及建设成本综合考量，高度控制在50m及以下的高层民用建筑较为常见。

8）实际工程中，为满足高层民用建筑的防火规范，可开启窗扇通常选用内平开内倒悬窗。内平开状态面积满足2%的防火规范下限要求，但日常采用内倒悬窗15°的状态来满足日常通风需求，此时，据《绿色建筑评价标准GB50378-2019技术细则》第55页5.2.10【条文说明扩展】，“当平开门窗、悬窗、翻转窗的最大开启角度小于45°时，通风开口面积应按外窗可开启面积的1/2计算”，其有效通风面积记作窗扇面积的一半，为1%。

9）实际工程中，常据《高层民用建筑设计防火规范GB50045-95(2005年版)》中8.2.2“需要排烟的房间/长度不超过60m的走道可开启外窗面积不应小于2%”取限值2%。

10）因2%至5%之间变化颗粒度较大，取中间值3.5%作为过渡值，构建连续、均匀变化的开窗洞口面积梯度。

11）实际工程中，常据《民用建筑设计统一标准GB50352-2019》第44页7.2.2“生活、工作的房间通风开口有效面积不应小于该房间地面面积的1/20”取限值5%。

12）实际工程中，常据《公共建筑节能设计标准GB50189-2015》第81页“如果外窗有效开启面积不小于锁在房间地面面积的8%，室内大部分区域基本能达到热舒适性水平”取限值8%。

13)风洞试验为软件开发团队委托国家空调设备质量监督检验实验中心实验室进行的，以北京市东城区兴化西里小区某典型住宅为原型按1:8等比例缩小搭建模型，应用CO2示踪气体衰减法测量房间内CO2浓度变化及分布情况，得到换气次数。在软件中搭建同一模型，所得模拟结果与风洞试验相比较的综合平均相对误差为10.18%。

14）计算流体力学（CFD）针对某一区域或房间（计算领域），建立质量、能量及动量守恒等基本微分方程，根据周边环境，设定合理的边界条件，然后利用划分的网格，对微分方程进行离散，将微分方程离散为代数方程，通过迭代求解，得到空气流动状况。采用CFD对自然通风模拟，主要用于自然通风风场布局优化和室内自然通风优化分析。由于建筑物周围的流动往往是湍流，模拟中常采用标准κ-ε模型及其它湍流模型方程。涉及到的控制方程主要包括：连续性方程、动量方程、能量方程。

15）换气次数=房间送风量/房间体积，单位是次/小时。

16）表1、表2、表3，以下简称“3个表”。

17）C2、C3、C4,以下简称“C2～4”。

18）综合观察3个表，C2～4、D2～43个数据的差值并不大，但A2～4中A2的数值跳脱，这与其平面分隔模式的特殊相对应：A3、A4均为走廊横向贯穿的双廊式平面，室外自然风需经由南侧开启扇流入、穿过南侧房间、流经走廊、穿过北侧房间再流出室外，流经路线复杂；A1为室内无遮挡的开放式平面，自然风畅通无阻；而A2平面作为介于开放式平面与双廊式平面的“缝合体”，左右两侧无分隔、中部为双廊，“过渡式”形态导致数值也处于两者之间。尤以A2的后两个数值表现明显，前2个数值绝对值较小，易受到统计误差的影响。

19）本文的分隔度变化特指建筑师大量采用的常规平面空间划分手法。