含复杂近邻的二维正方格子键渗流的蒙特卡罗模拟*

寻之朋 郝大鹏

(中国矿业大学材料与物理学院,徐州 221116)

1 引言

渗流模型蕴含着丰富的物理,是统计物理学领域的基础模型之一[1-6].一方面,研究渗流模型对理解自然界中的相变和临界现象、分形、标度理论等均有着重要的科学价值.另一方面,渗流具有广泛的应用,如流体流经多孔物质、森林火灾、流行病的传播(如最近爆发的新冠肺炎)等.因此,对渗流的深入研究具有重要的理论价值和现实意义.

建立各种格点渗流模型是研究渗流常用的方法之一.在指定格点模型上,每一个格点(或键)是独立的并以一定的概率p被占据(不被占据的概率为 1-p),被占据的格点(或键)可以形成毗连的团簇.当占据概率p从 0 逐渐增大到某一临界值时,格点模型上将开始出现大到能够贯穿整个系统的团簇,并且这时的系统通常表现出连续相变的特性,称这样的系统为渗流,并且称此时的临界概率为渗流阈值,用pc表示.渗流阈值pc是渗流的核心参数之一,只有准确地确定渗流阈值,才能更好地研究其临界行为以及确定临界指数.

无论从解析角度还是采用蒙特卡罗模拟等数值方法,许多格点模型被广泛研究以获得渗流阈值pc以及相应的临界指数.在众多格点模型中,含复杂近邻的格点渗流模型由于多方面的应用而成为该领域的热点研究课题之一.例如,该类模型点渗流可以镜像到格点模型上扩展形状(如圆形、球形)的吸附渗流过程[7,8].键渗流不仅与小世界网络有着密切的联系[9],还可以从渗流的角度去研究分析流行病的传播过程[10,11].其次对这类渗流模型的深入研究,既能丰富相关的渗流理论,又对研究渗流阈值与格点模型的结构,尤其是格点配位数之间的关系具有重要的指导作用.此外,这类格点渗流模型的结构介于离散渗流与连续渗流之间,对其进行深入探讨也有助于揭示离散渗流和连续渗流之间转变的物理机制.

对含复杂近邻的格点渗流模型的研究可以追溯到由Dalton,Domb 和Sykes[12-14]提出的“等效近邻模型”.之后,研究人员在该方向开展了广泛的研究,如菱形结构紧密区域的长程点渗流[15],考虑最近邻和次近邻的体心立方格子的点渗流和键渗流[16],含第四近邻格点的面心立方格子的点渗流[17]等.d’Iribarne 等[18-20]从图论的角度系统计算了长程关联(最大计算到了第10 近邻格点)的全部11 种阿基米德格子的点渗流.Malarz 和Galam[21]引入“复杂近邻”的概念,即不同近邻格点的各种组合而并不局限于紧密近邻格点,随后该课题组对二维正方格子、三维简单立方格子、四维超立方格子的点渗流开展了一系列的研究工作[22-26].最近,基于多种有效算法的发展,含复杂近邻的格点模型的键渗流也得到了广泛的研究[27-30].

渗流阈值pc与格点模型结构(如配位数z)之间的依赖关系一直是探讨的焦点之一.例如文献[23]指出一些三维格点模型的点渗流阈值与格点配位数之间满足幂律关系pc～z-a,指数a=0.790(26) .Galam 和Mauger[31],van der Marck[32],以及其他研究人员也分析研究了许多其他体系,得出类似的幂律关系[29,30].Domb[12]指出在相同的格点单元形状下,含扩展近邻的格点模型点渗流在配位数z较大时的渐近行为与连续渗流阈值ηc有关;该论点得到了其他学者的赞同和推进[7,8,20],最近更深入的研究[33]揭示出该渐近关系为pc～2dηc/z.对于键渗流,该渐近关系趋于Bethe 格子的结果pc～1/(z-1);以及当z为有限值时满足有限尺寸修正zpc-1～a1z-x,其中在二维及三维情况下x=(d-1)/d[34,35].这些理论分析结果均得到了大量数值模拟工作的验证[27,28,33,35].

但是,以上渐近行为及有限尺寸修正行为仅对含紧密近邻的格点渗流模型是有效的,而对于含复杂(非紧密)近邻格点渗流模型的分析却遇到了困难.其主要原因是这类格点渗流模型表现出所谓的“简并”现象,即一个配位数z对应于多个格点模型结构,如图1 所示的含复杂近邻格点的二维正方格子(图中“•”代表中心格点,①代表最近邻或第1近邻格点,②代表次近邻或第2 近邻格点,······),“第1 近邻+第2 近邻”与“第1 近邻+第3 近邻”所对应的配位数是相同的,均为8;但是这两种结构的渗流阈值却是不相同的.因此,对于这类格点渗流模型,仅仅考虑配位数一个参量是不够的,如何综合考虑格点模型的拓扑结构来消除“简并”是解决该问题的关键所在.

图1 正方格子中心点(“ • ”)的近邻格点,到第 5 近邻Fig.1.Neighbors of a central site (“ • ”) on a square lattice,up to 5 th nearest neighbors.

为了更深入地探讨渗流阈值与格点模型的几何或拓扑结构之间的关联,本文基于图论[36]、有机化学[37,38],以及最近Malarz[39]关于点渗流中模型参数识别的基本思想,引入新的标量参数ξ=其中zi和ri分别为第i近邻格点的配位数及其到中心格点的距离,综合地考虑格点渗流模型的拓扑结构来消除这种“简并”,并将该标量参数应用于研究分析含复杂近邻的格点模型的键渗流.同时,基于一种高效的单团簇生长算法对含复杂近邻的二维正方格子键渗流进行了大量的蒙特卡罗模拟研究,得到了这些格点渗流模型高精度的键渗流阈值.所得到的渗流阈值与新的标量参数很好地满足幂律关系pc∝ξ-γ,数值拟合得指数γ≈1 .

2 理论基础

团簇的统计分布是研究渗流的一个中心物理量,通过该分布的特性即可确定渗流阈值及相应的临界指数.首先定义团簇的尺寸为一个团簇中所含格点(或键)的个数,用s表示.则团簇的分布通常用ns(p) 表示,它是指在占据概率p下,尺寸为s个格点(或键)的团簇的数目.在实际使用时,将对团簇的分布进行归一化处理.在渗流阈值pc处,ns(pc)满足关系式

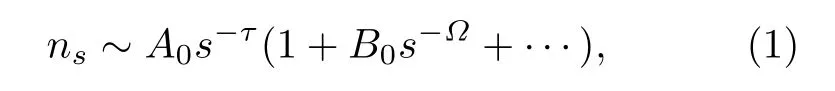
其中,τ为Fisher 指数,Ω为幂律关系的一阶修正指数.τ和Ω均被认为具有普适性,只与系统的维度有关.A0和B0为与具体的模型有关的两个参数,是非普适的.由(1)式可得出模型上每个格点(或键)属于尺寸大于或等于s的团簇的概率为

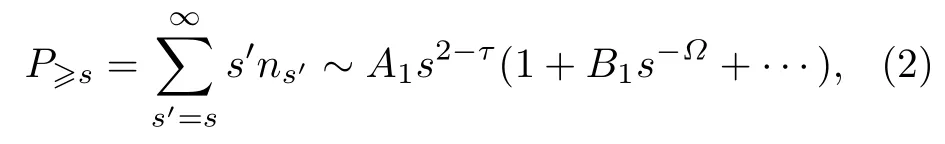
其中,A1=A0/(τ -2),B1=(τ -2)B0/(τ+Ω-2) .(2)式两边同时乘以sτ-2得

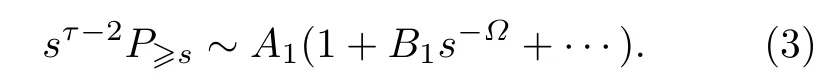
可以看出,当s较大时,sτ-2P≥s随s-Ω的变化将呈线性关系.利用该线性关系可以确定渗流阈值,因为当p/=pc时,关系是非线性的.

当p/=pc时,需要引入标度函数.在标度极限s →∞和p→pc下,(p-pc)sσ趋于常数,P≥s满足

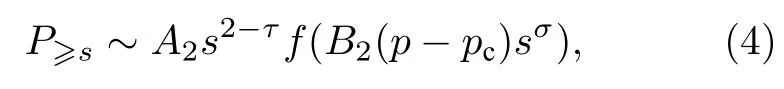
式中σ为另一普适指数.对标度函数f(x) 作泰勒展开

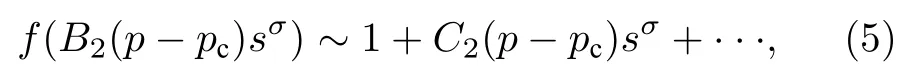
其中,C2=B2f′(0) .这里假设f(0)=1,将(5)式代入(4)式可得

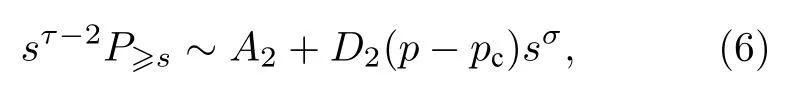
其中D2=A2C2.(6)式表明,当s较大时,sτ-2P≥s在p→pc时将趋于常数,而在p远离pc时将偏离该常数.这提供了确定渗流阈值的另一个途径.

3 数值模拟结果与分析

单团簇生长算法的基本规则[29,30]如下:在格点模型上任取一个格点作为种子,以该种子为起点开始生长单独的团簇.在周期边界条件下,格点模型上任意一个格点都可以作为种子,本文在数值模拟中选取为坐标原点.从种子格点开始,团簇以一定的概率p占据(不被占据的概率为 1-p)与之连接的键从而向近邻格点生长.在系统尺寸为L×L=16384 × 16384 的正方格子上,针对每一个格点渗流模型,独立地生长不少于 5×108个系综(即独立的团簇).从统计上来讲,这些团簇具有不同的尺寸,尺寸较小的团簇将很快停止生长,而有的团簇则可以生长到很大的尺寸.因此在实际的数值模拟中,需要设定团簇生长的上临界截断阈值尺寸来避免出现边界环绕,同时控制程序运行时间,当团簇的生长达到预设的上临界截断阈值尺寸时停止生长.然后,将尺寸落在区间 [ 2n,2n+1-1] (n=0,1,2,···)内的团簇的数量记录到结果向量的第n个值中.对于达到上临界截断阈值尺寸仍在生长的团簇,它将被统计到结果向量的最后一个值中.对于本文所模拟的所有格点模型,上临界截断阈值均设置为 216,这也就意味着结果向量的长度为17.采用单团簇生长算法在数值模拟中不需要存储记录大量的中间迭代数据,仅需要对结果向量进行处理即可,这是该算法优于其他方法的一个方面.此外,新的单团簇生长算法[29,30]在原有的基础上采用了有效的技术手段对算法进行改进,成功地避免了每次单个团簇生长之后将整个格点模型信息清除.优化的基本思想如下:将每个格点的初始值设置为零,对于第n个团簇(对应于统计系综次数),晶格模型上任何值小于n的格点都被视为未被占据.当一个格点在新团簇生长的过程中被占据时,其值赋为n.这个过程节省了大量时间,因此我们可以模拟非常大的晶格尺寸,并且不必在每个团簇(实际上许多团簇都很小)生长之后清除整个晶格的信息,使计算效率得到了显著的提高.在文献[29]中,我们给出了该优化算法的程序伪代码.

对于普适的标度指数,目前已得到二维情况下的解析 解τ=187/91,σ=36/91和Ω=72/91,本文在数值分析中直接使用这些普适参数值.于是根据蒙特卡罗模拟数据,相应的物理量,如sτ-2P≥s,便可易于计算得到.

本文使用 S Q-a,b,···来表示含第a近邻,第b近邻,······的二维正方格子.基于理论公式(6),图2为在占据概率分别为 0.250365 ,0.250367 ,0.250368,0.250369 及 0.250371 时 S Q-1,2 格子 键渗流sτ-2P≥s随sσ的变化曲线.可以看出:当团簇尺寸s较小时,由于有限尺寸效应,sτ-2P≥s随sσ急剧下降;当s较大时,sτ-2P≥s随sσ的变化逐渐表现出线性行为,并且随着占据概率p趋于渗流阈值pc,曲线逐渐趋于水平,即趋于常数.根据图2 中线性部分的性质,对每一个占据概率下曲线的线性部分计算斜率,渗流阈值的中心值可以通过作图

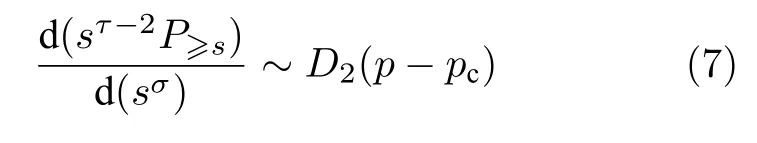
来进行确定,如图2 中的插图所示.通过插图中的线性部分与横轴的交点,可以确定渗流阈值的中心值为pc=0.2503683 .

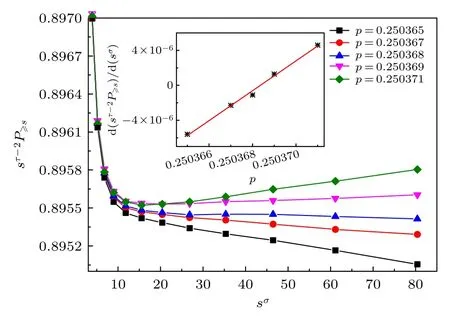
图2 SQ-1,2 格子键渗流在不同占据概率p 下sτ-2P≥s随 s σ 的变化曲线,其中 τ =187/91 ,σ =36/91 .插图表示主图中所示结果线性部分的斜率随占据概率p 的变化关系Fig.2.Plot of s τ-2P≥s vs.s σ with τ =187/91 and σ=36/91 for the bond percolation of the S Q-1,2 lattice under different values of p.The inset indicates the slope of the linear portions of the curves shown in the main figure as a function of p.

另一方面,基于理论公式(3),在占据概率分别为p=0.250365 ,0.250367 ,0.250368 ,0.250369,以 及 0.250371 时 S Q-1,2 格子键渗流sτ-2P≥s随s-Ω的变化曲线如图3 所示.由图3 可以很明显地看出,当占据概率p偏离渗流阈值pc时,曲线表现出明显的偏离线性行为;而当占据概率p逐渐趋于渗流阈值pc时,曲线表现出越来越好的线性行为.于是,通过图3 可以确定键渗流阈值的范围为0.250368＜pc＜0.250369.

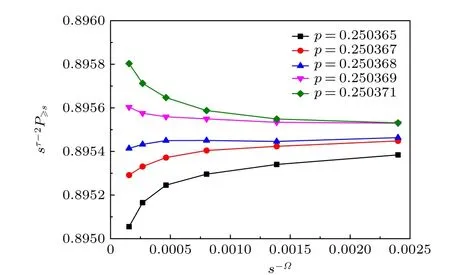
图3 SQ-1,2 格子键渗流在不同占据概率p 下sτ-2P≥s随 s -Ω 的变化曲线,其中 τ =187/91 ,Ω=72/91Fig.3.Plot of s τ-2P≥s vs.s -Ω with τ =187/91 and Ω=72/91 for the bond percolation of the S Q-1,2 lattice under different values of p.

综上两种方法,可以确定 S Q-1,2 格子键渗流阈值为pc=0.2503683(7),其中括号里面的数字表示阈值末位的误差.对于本文所模拟的其他格点模型,其分析过程与上述类似;因此不再赘述每一个格点模型具体的结果图形及分析过程,而是直接给出键渗流阈值的数值处理结果,并将结果总结在表1 中.

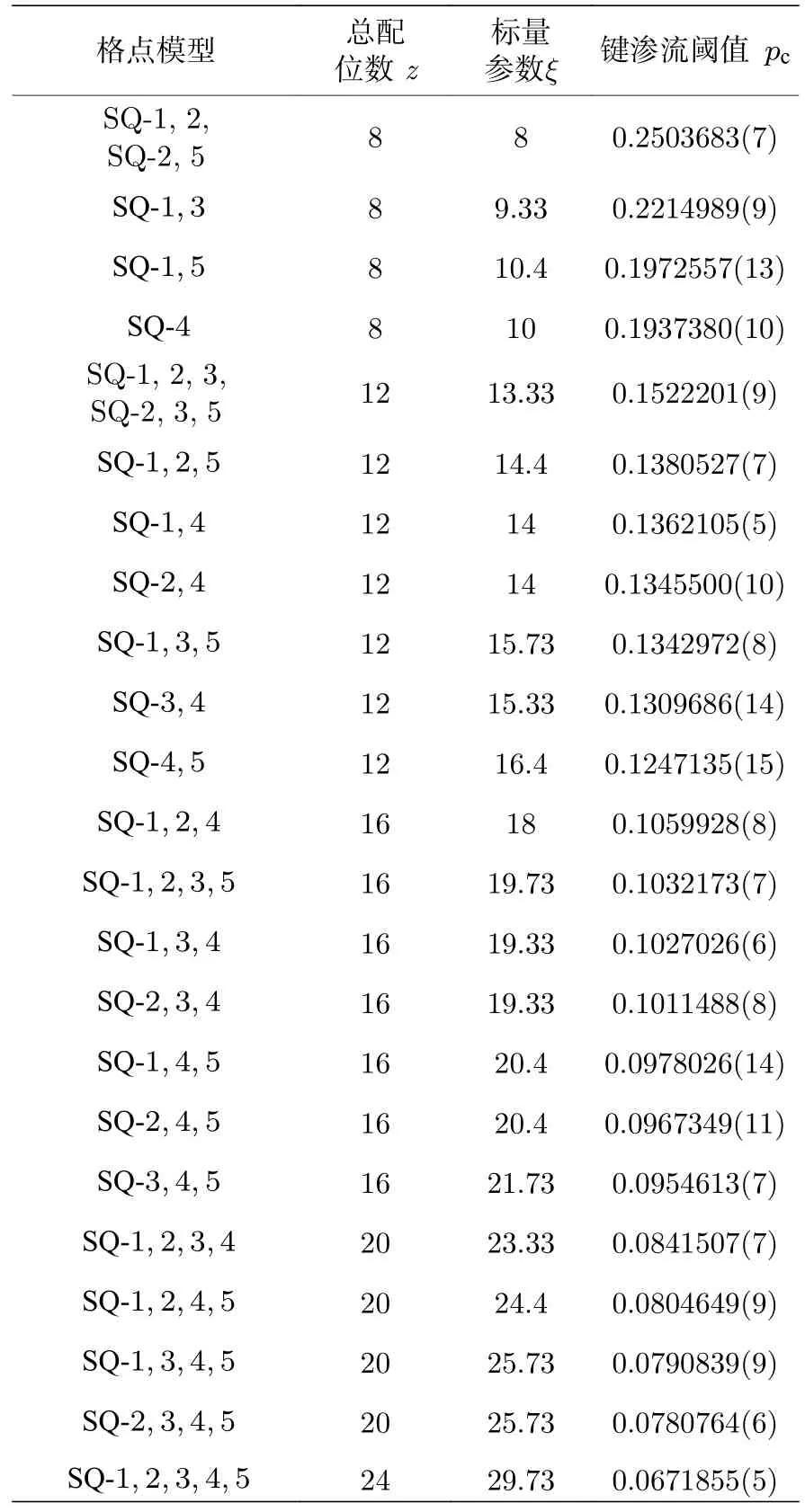
表1 含复杂近邻格点的二维正方格子的键渗流阈值Table 1.Bond percolation thresholds of square lattice with complex neighborhoods.

表1 第2 列给出了每一个格点模型的配位数z.可以看出存在明显的“简并”现象,即许多不同的格点模型具有相同的配位数z,但键渗流阈值却不相同.图4 给出了这些格点模型键渗流阈值pc随格点配位数z变化的对数-对数曲线,也可以明显地看出“简并”行为.这些结果说明,对于含复杂(非紧密)近邻的格点渗流模型,渗流阈值不仅仅取决于格点配位数,而需要对格点模型的其他几何参数进行更深入的分析.

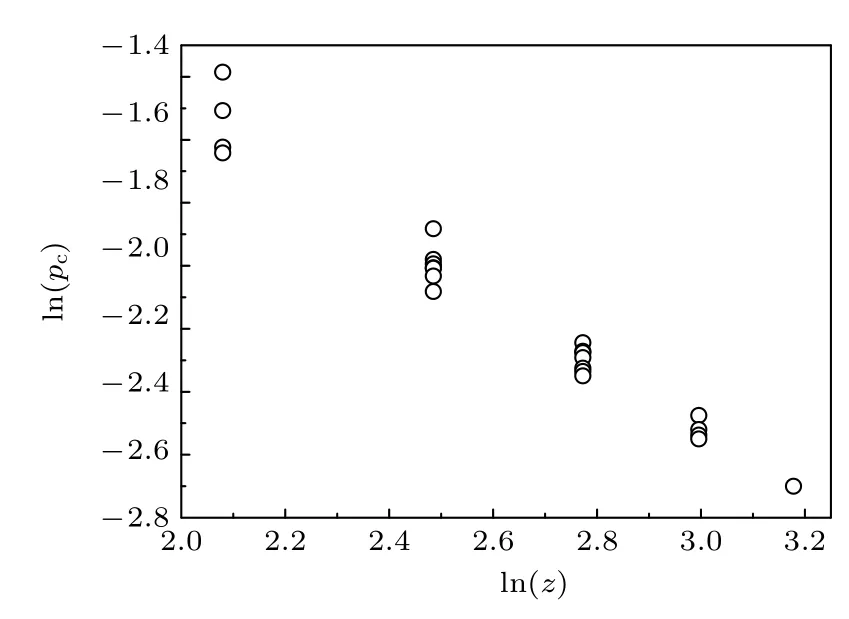
图4 表1 中所示格点模型 pc 随z 变化的对数-对数曲线Fig.4.The log-log plot of pc vs.z for the lattices shown in Table 1.

以上分析表明需要采取有效的技术手段,引入新的参数来消除“简并”.最近,Malarz[39]综合考虑第i近邻格点的配位数zi以及其到中心格点距离的平方引入了新的标量参数

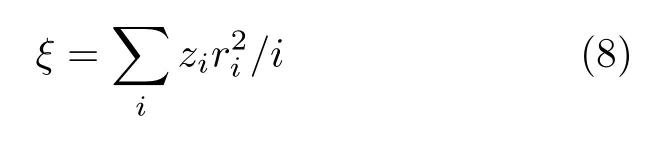
来有效消除“简并”,并将其应用于分析含复杂近邻格点的二维三角格子的点渗流,取得了成功.实际上,这种消除简并的方式在图论中分析树结构的拓扑不变性[36],有机化学中分析分子拓扑指数[37,38]等方面也有成功的应用.本文尝试采用这种方法来分析含复杂近邻二维正方格子的键渗流.首先,根据(8)式计算得到每一个格点模型对应的标量指数ξ,如表1 中第3 列所示.对应于不同近邻格点的zi和ri2参见表2.从计算结果可以看出,引入新的参数后,在很大程度上消除了“简并”现象.然后,作出渗流阈值pc随参数ξ变化的对数-对数曲线,如图5 所示.结果显示,渗流阈值pc随ξ的变化呈现出很好的幂律关系pc∝ξ-γ,并且线性拟合得到幂律指数γ≈1 .可见,(8)式消除简并的方法也能够成功地应用于含复杂近邻格点模型的键渗流.

表2 正方格子不同近邻格点的相关参数Table 2.Parameters of different nearest neighbors on square lattice.

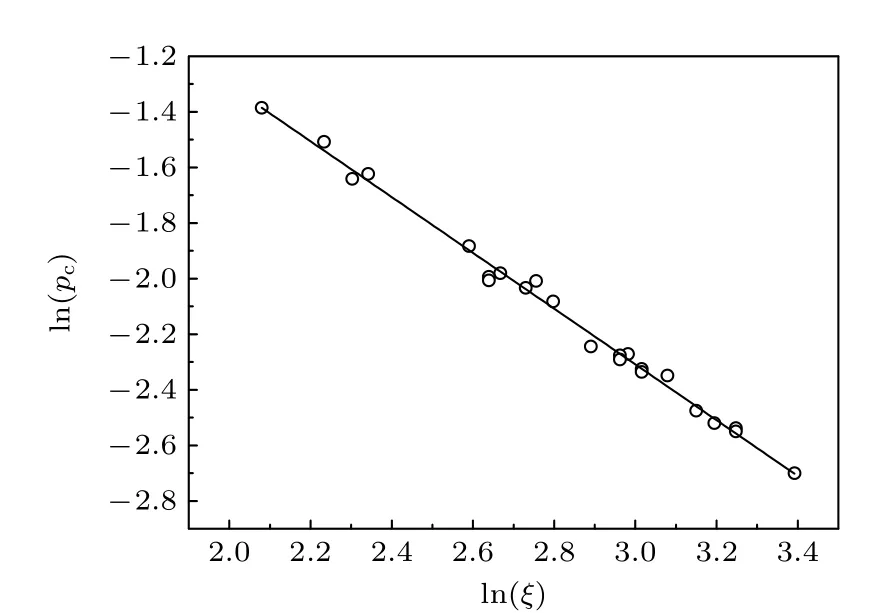
图5 表1 中所示格点模型 pc 随ξ 变化的对数-对数曲线Fig.5.The log-log plot of pc vs.ξ for the lattices shown in Table 1.

4 结论

综上,为了深入分析渗流阈值与格点模型结构之间的关系,本文基于高效的单团簇生长算法,对含复杂近邻的二维正方格子键渗流进行了大量的蒙特卡罗模拟研究.得出主要结论如下:

1) 单团簇生长算法能够有效地模拟含复杂近邻的格点模型的键渗流,并获得了高精度的键渗流阈值.对于这类格点模型,由于模型中存在交叉(非相交)键,这在很大程度上限制了之前许多算法或方法的有效应用,而单团簇生长算法则提供了模拟此类格点模型的有效途径.