基于局部密度信息熵均值的密度峰值聚类算法
唐风扬,覃仁超,熊 健
(西南科技大学 计算机科学与技术学院,四川 绵阳 621010)
0 引言
近几年,随着全球存储信息量与数据量的爆炸式增长,在给各行业带来机遇的同时也带来了巨大的挑战,即如何高效地处理这些信息与数据。聚类算法作为数据处理的关键技术,本质是将一组数据划分为不重叠的子集的过程,每个子集都是一个聚类,所以同一聚类中的点彼此相似,而与其他聚类中的点不相似。聚类算法不仅是数据挖掘的一种重要手段,还是机器学习理论与技术中的重要数据预测和分析方法之一,在模式识别[1]、图像处理[2]、文献计量学,生物信息学等领域得到了广泛应用。
1 研究现状
聚类算法常用在无监督学习中,算法通过学习未作标记的样本以此来揭示数据的内在规律,完成数据的分类。随着近年来不断的深入研究,通常将其分为以下几类,基于划分的聚类如K-MEANS[3]算法,然而该算法聚类效果的好坏取决于人工选择的聚类中心且有着对样本中的异常点敏感的缺点。为此衍生出了利用聚类中心相互间隔距离较远思想的K-MEANS++算法,虽然方法简单,但非常有效;而改变中心点选取策略的K-MEDOIDS算法在小样本的数据中有着更好的噪声鲁棒性;利用遗传算法,粒子群等优化算法进行初始值寻优的多种改进方法都有着良好效果。其他经典算法中有将空间划分为矩阵,基于网络多分辨率聚类技术的STING[4]算法和利用层次方法进行聚类和规约数据的BRICH[5]算法。DBSCAN[6]算法作为具有代表性的密度聚类算法,提出了密度可接近性与密度可连性的概念,将具有足够密度大小的区域划分成簇,在带噪声的空间中能识别形状各异的簇,但参数的人工选择限制了算法的效果。而为了解决这个问题,OPTICS[7]算法应运而生,算法为聚类的分析生成簇的排序,从这个排序中可以得到DBSCAN算法的多种聚类结果。这些算法在性能上有很大差异,如K-MEANS只能识别凸球形簇,STING算法具有很快的速度,但是准确度不高,而BRICH算法可以简单对数据进行预处理并识别噪声点,但在数据是非超球体的分布簇的情况下效果一般。DBSCAN在不规则簇的识别上效果显著,也有不错的抗噪声能力,但在面对数据维度升高时效果明显下降[8]。
2014年6月,Rodriguez等人在Science上发表了DPC[9]算法,这是一种基于距离和密度的算法,能够找到任意形状的聚类中心,与传统算法相比,该算法无需迭代目标函数就能找到高密度点,并且实现简单。然而该算法需要通过经验设置距离阈值dc完成密度的计算。目前为止许多学者对算法进行了改进,其中一部分改进算法根据数据集自身数据情况自适应求得最佳距离阈值dc[10-14],这种做法一定程度上优化了距离阈值dc的选择,但各方法的适用数据集不同。文献[15]通过构建Ball-Tree 缩小样本局部密度和距离的计算范围减少了计算量,文献[16]基于块的不相似性度量计算样本间的相似度,引入样本的 K近邻度量,定义新的局部密度。文献[17]等通过改变聚类中心的定义,并将邻域中的密度极值点确定为聚类中心,然后会选择到超过簇数目的聚类中心,文献[18]等引入K近邻的思想来计算距离阈值dc和每个点的局部密度,文献[19]等定义了从属的概念来描述相对密度关系,并使用从属的数量作为识别聚类中心的标准。文献[20]等利用网络划分的方法,解决计算欧氏距离时花费过多时间的问题。文献[21]等不仅引入KNN思想解决局部密度的计算,并且运用PCA对高维数据降维。
本文针对距离阈值dc选择存在的问题,定义局部密度捕获范围并利用局部密度信息熵均值进行优化,通过设置距离阈值一定倍数的参数确定局部密度捕获范围,使得在分类错误的情况下通过对相对距离进行密度的加权重新获得正确的分类数量和分类中心。通过DPC算法与信息熵的结合使用,即使在不规则图形中也能够排除异常点的干扰,准确快速地找到正确的分类中心和分类数量,实验证明在不同的数据集中均取得了良好的效果。
2 密度峰值聚类算法
2.1 算法原理
DPC算法认为簇中心拥有如下特征:(1)数据点与其他密度大的点有相对远的距离[22];(2)数据点本身密度大于包围它周围的点。通过定义ρi和δi来表示数据点的密度与相对距离,然后选取两者中双方值都相对较大的点作为簇中心,最后将其他非中心点归到其最近的更高密度点完成聚类。
2.2 算法过程
首先通过计算得到对于数据集S={x1,x2,x3,...,xn}中,数据点xi与xj的欧氏距离dij,计算公式如式(1):
(1)
计算数据点xi的局部密度ρi。
截断核计算公式如式(2):
(2)
dij为数据点xi与xj的欧式距离,dc为能囊括总数据量1%至2%的距离阈值,其中函数X如式(3)所示:
(3)
高斯核计算公式如式(4):
(4)
截断核以离散值估计出的密度全为整数,有重复值,而高斯核以连续值估计出的密度因此不会产生重复值,因此当不同点拥有相同局部密度的情况下使用高斯核进行计算会取得更好的效果,故本文中采取高斯核密度计算公式。
计算数据点xi的相对距离δi,公式如式(5)~(6):
(5)
(6)
公式(5)中δi表示对于数据点xi,到有高于它局部密度点的最近距离,(6)中δi是当其数据点xi在数据集S中局部密度最大时的距离。一般密度大的数据点的距离参数δi要比其它邻近点大。
在计算完每个点的局部密度ρi和相对距离δi之后,以密度为横坐标,相对距离为纵坐标画出相对距离/密度图在其中选取密度和距离值相对大的点作为聚类中心。不过文献[4]中提到通过设置决策函数:
γi=ρi×δi
(7)
来绘制决策图赋值确定聚类中心。其中具有更大γi的点xi会具有更高成为聚类中心点的可能性。为此,将γi降序排序,在二维平面图中画出决策图,找到γi较大的点xi作为聚类中心,DPC算法将非中心点归并到密度比当前点高且距离最近点以完成聚类。
2.3 算法的不足
DPC极其依赖参数距离阈值dc的选择,相同的数据集在不同的距离阈值dc下有非常大的差别,在Rodriguez等人的文章中指出dc选择能囊括总数据的1%~2%数量(下文简称dc=n%)的数值,这种局限性突出在一些特殊的数据集中,并且对不同的数据集难以进行距离阈值dc的选择。
目前普遍认为距离阈值dc选择过小时,可能会在同一簇内找出多个密度峰值,从而得到过多的聚类中心导致聚类失败,极端情况下距离阈值dc小于数据集中各个点的最小欧氏距离,这时每个数据点都将单独成为一个类别;如果距离阈值dc选择过大,会使得区分度过低,从而不同的簇往往会被分到同一聚类中心,导致簇中心的少选从而聚类失败,极端情况是距离阈值dc超过了数据点中各个点的最大欧式距离,这会把所有数据归为一个类别。
3 基于局部密度信息熵均值优化的聚类算法
3.1 信息熵
假设X为随机型离散变量,那么它在有限范围内的取值R={x1,x2,x3,...,xn},而其中xi出现的概率为Pi,同时设Pi=P{X=xi},则对于x信息熵的公式定义为式(8)所示:
(8)
信息熵作为一种计算属性权重的经典算法一般用来计算数据的离散度。熵值一般与离散程度成反比,即数据某指标越小的熵值说明该指标离散程度越大,同时该指标也有更大的信息量。
3.2 局部密度捕获范围
针对DPC算法在计算相对距离和密度时并未考虑数据点空间分布特性的影响,而是从全局的角度出发通过使邻近样本数占比达到全部样本的一定数量,计算距离阈值来确定密度进而算出相对距离的时候数据密度和相对距离分布不均匀,多个密度峰值被划分至同一个聚类中心和一个簇中心存在多个密度峰值的问题。
本文提出一种局部密度捕获范围,用来捕获数据点附近一定范围内的点以供后续计算使用,通过设置参数w来确定某点的局部密度捕获范围。
定义1:局部密度捕获范围。局部密度捕获范围表示能包含某一区域内全部数据点的范围,记作w如式(9)所示:
w=c×dc
(9)
其中:参数c在多次实验中显示取距离阈值dc的0.5~5倍时有最佳效果。
3.3 局部密度信息熵均值的计算
本文中将信息熵与局部密度相结合,通过计算某点的局部密度信息熵均值,确定该点相对于周围点的密度分布情况。相对距离相近但局部密度不同的点,在决策图上通常难以区分,但可以通过以其相对距离乘以局部密度信息熵均值来解决,在相对距离相近的情况下,局部密度相差小的点相对局部密度相差大的点拥有更大的局部密度信息熵均值,从而让局部密度相差大的点的相对距离变小,进而使决策图中的相应的值变小,以此来区别出数据密度点中可能被误分为聚类中心的点。
定义2:局部密度信息熵均值。局部密度信息熵均值表示局部范围内数据点的分布情况,某一点的局部密度信息熵的值与该点附近密度分布离散程度成反比,记作H(X)。
局部密度信息熵均值的计算公式如式 (10)所示:
(10)
其中:
(11)
N为点xi半径小于局部密度捕获范围w内的所有点的数量。
在加权之后由于权数值较小,故为使加权效果更加显著,在反复实验中类比sigmoid,log等函数之后发现log一类的对数函数由于没有明确上界会将密度较大的点的相对距离过于放大,从而难以产生效果,而sigmoid函数无法产生有效的区分度,但使用反正切函数acrtan能够更好地将正确簇中心与错误簇中心区别,故选用使用反正切公式来处理H(X)得出全新加权系数H′(X)如式(12)所示:
(12)
3.4 加权后相对距离
使用原相对聚类δ新加权系数H′(X)相乘得到加权后相对距离δe如式(13)所示。
δe=H′(X)×δ
(13)
3.5 新的决策函数γe
使用新的加权相对距离δe与密度ρ相乘得到γe如式(14),从而绘制新的决策图。
γe=ρ×δe
(14)
3.6 聚类中心的选取
如图1所示,点A和点B属同一簇,但点B具有较高的局部密度和距离δ,在DPC中在距离阈值dc取值较小时会把A,B点看作两个聚类中心点,而LDDPC算法通过对相对距离δe进行加权,使得B的相对距离δe变小,从而将A,B点归为同一簇中完成正确的聚类。

图1 错误聚类示例
经过反正切公式(11)和相对距离加权公式(12)的运算之后,在γe上决策图的聚类中心变得清晰可分。在决策图中很容易看到非聚类中心点之间排列紧密,且相互之间的差值非常小,这时只需选取决策函数γe较大且相互差距大的点作为聚类中心即可。经LDDPC算法处理后相比DPC算法能够更快速更直接地选取正确的聚类中心。
4 算法流程
算法处理流程如下。
步骤1:输入待检测的数据集S={x1,x2,x3,...,xn}和dc以及参数w;
步骤2:将数据集按照公式(1)求出欧氏距离;
步骤3:分别代入公式(4)~(6)求出每个数据点xi的ρi与δi;
步骤4:按照公式(10)~(12)算出每个数据点的局部密度信息熵均值H(X)和加权后的系数H′(X);
步骤5:根据公式(13)和公式(14)算出加权后每个点xi的相对距离δei以及γei;
步骤6:根据γe的决策图计算出聚类中心;
步骤7:将每个数据按照最近距离数据点的类别分类;
步骤8:输出实验结果。
5 实验与分析
5.1 实验环境
LDDPC算法通过python3.7.9实现与处理。实验环境:操作系统为win10 64位,CPU为I5-7300HQ,主频2.5 GHz,内存为16 G。为了验证算法性能,将在下文的实验中把DPC算法与LDDPC算法效果相比较。
5.2 实验说明
实验一与实验二数据集详见表1,为了验证算法的有效性和适应性,故实验中选取的dc值中即有小于1%,大于2%也有1%~2%正常取值区间内DPC算法无法正常发挥效果的值,通过实验验证错误聚类中的聚类过多和过少的情况下LDDPC算法仍能发挥的效果。

表1 实验一与实验二所用数据集
5.3 实验一:DPC算法分类错误时通过LDDPC算法获得正确分类
图2至图4为在Aggregation数据集中,当dc=1.3%时的效果图,决策图和聚类结果图,图2为密度ρ和相对距离δ的原始分布,图(a)为原始算法得出的分布情况而图(b)为LDDPC算法处理后(即密度ρ和加权后相对距离距离δe)的分布,图3和图4中可以看到图(a)DPC算法中簇数过多而导致分类的失败,决策图中能看到超过簇数7个的相对大的γ值,而图(b)LDDPC算法处理后,在决策图上能够明显分辨出7个相对大的γe值,从而成功分为7个类。在图5至图7为数据集Flame中,为dc取值为3.6%时的对比图,从图5(a),图6(a),图7(a)中可以明显看出距离阈值取值的失败导致出现4个簇中心的多分类情况,此时同一个簇中拥有多个聚类峰值,而在图5(b),图6(b),图7(b)中在LDDPC算法的处理下决策图中仅出现2个相对较大的γe值,说明同一簇中多余的聚类峰值的消失,于是数据成功分成2个类别。

图2 在Aggregation数据集下的相对距离/密度图对比图

图3 在Aggregation数据集下的决策图对比图
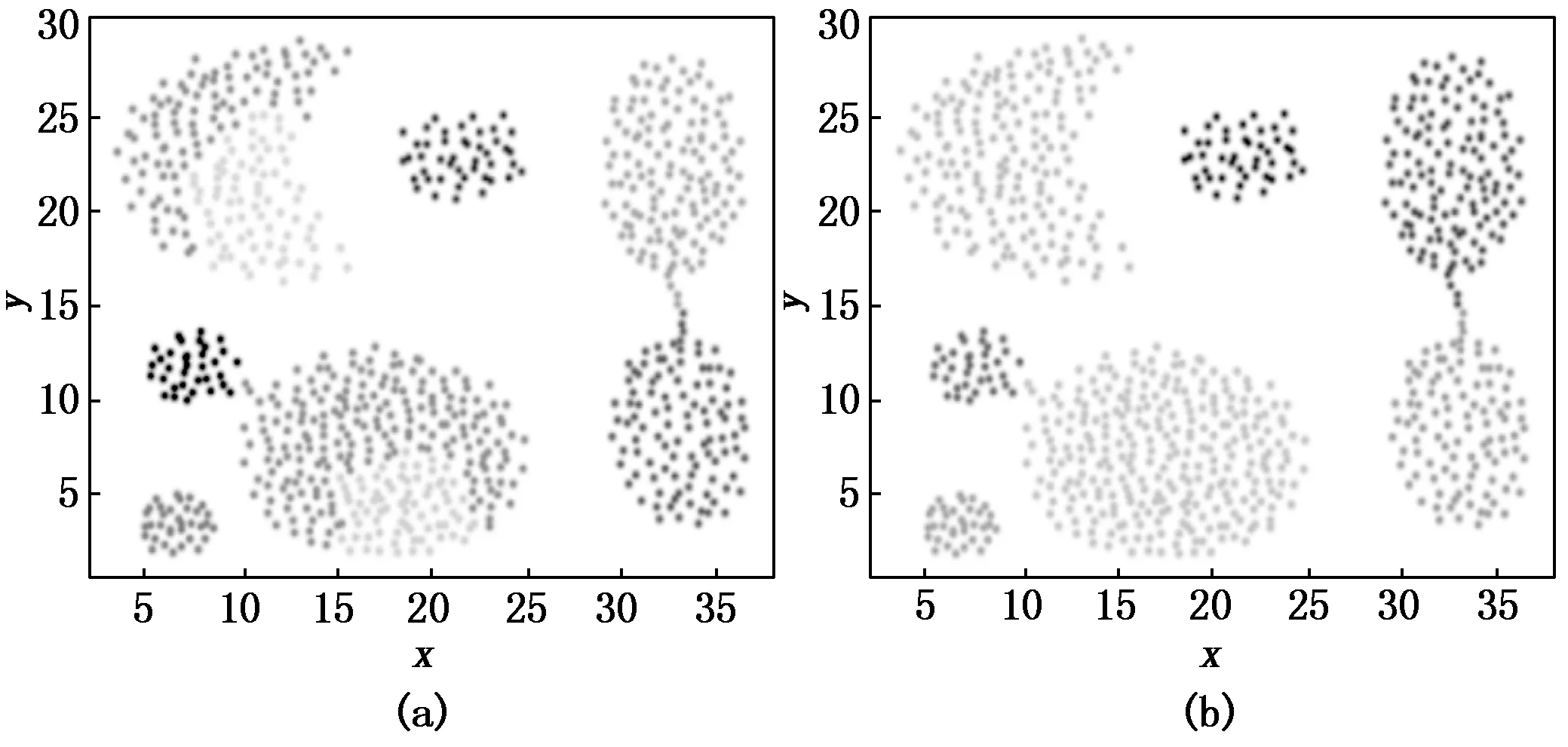
图4 在Aggregation数据集下的聚类结果对比图

图5 在Flame数据集下的相对距离/密度对比图
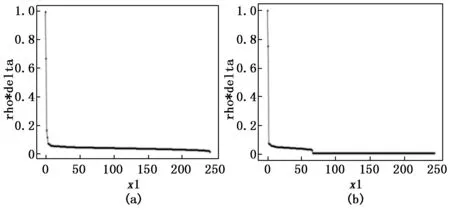
图6 在Flame数据集下的决策图对比图
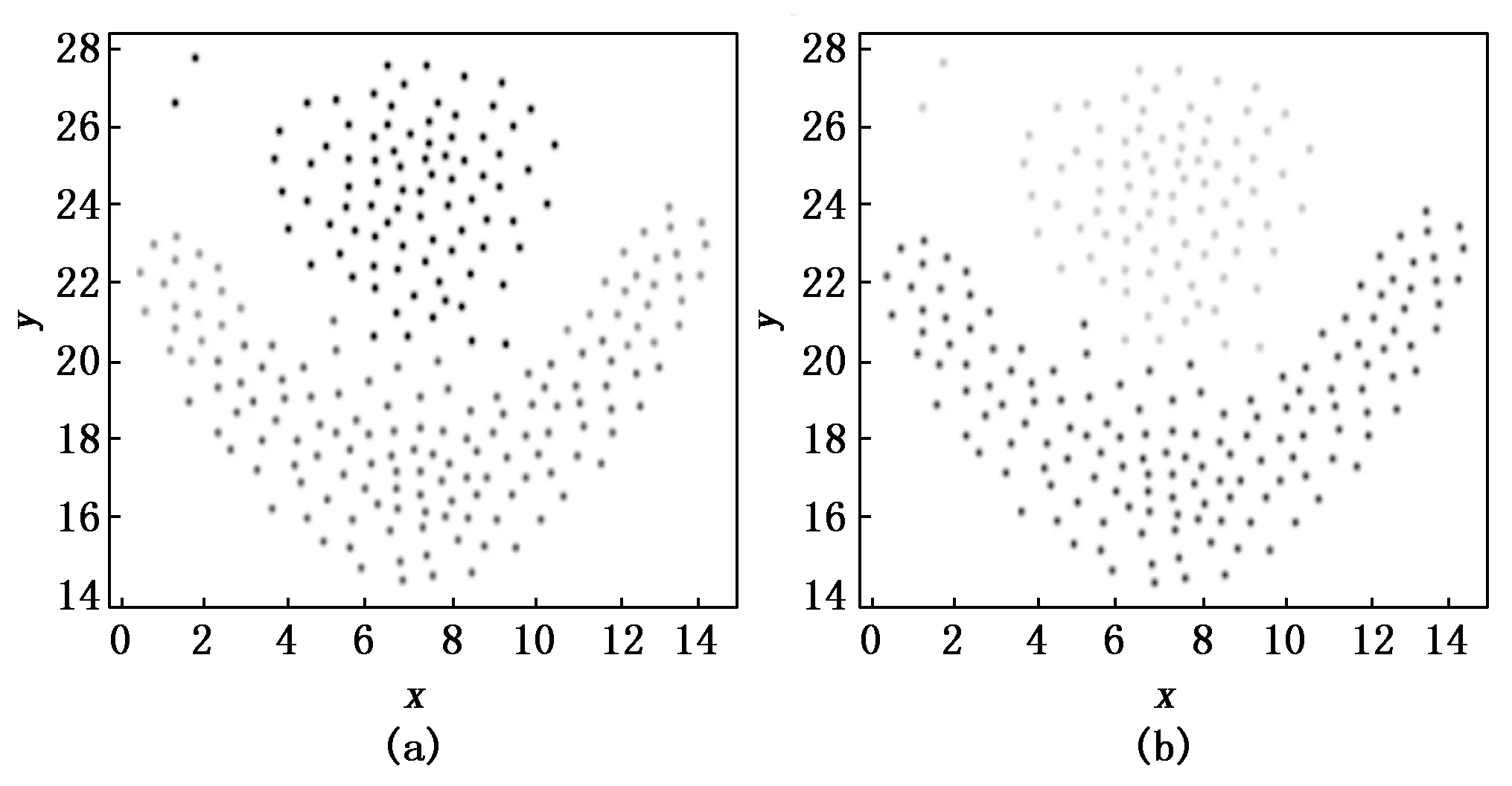
图7 在Flame数据集下的聚类结果对比图
通过实验可以看到以上数据集均被错误地分成了多个类别,并且从决策图可以看出分布并不明显,稍有不慎就会误选,将密度ρ和相对距离δ乘积γ较大的点选为聚类中心,导致同一簇中存在多个聚类峰值的情况,而在LDDPC算法下通过γe构建决策图从而被正确的分类,并且新决策图中γe值显示非中心点与中心点具有更大的差值,相比原决策图更加清晰可分,不会因不慎而错选多选而导致出现不正确的簇数的情况出现。
5.4 实验二:DPC算法分类正确时获得更加清晰的决策图
图8至图10展示了R15数据集在dc=2%时正确聚类情况,通过图8和图9的对比可以看出,在LDDPC算法的处理下,相比DPC算法中原来的相对距离δ,经局部密度信息熵加权后的加权相对距离δe具有更大的值,聚类中心点和非中心点在新决策图中的γe值与原决策图中的γ值相比差值变大,这使在决策图中寻找聚类中心时更加容易。同理图11至图13是数据集D31在dc=2%时,经过LDDPC算法处理前后的对比,图11(a)与图11(b)相比DPC算法区分度更明显,相对距离δ整体上移,在决策图中同样体现为γe值的整体上移,与R15中同样在处理后增加了决策图的辨识度,能够更好地把真实簇中心从其他高密度峰值的虚假簇中心中分离,从而能够更加精确快速地完成31个类别的数据集的分类。

图8 在R15数据集下的相对距离/密度对比图

图9 在R15数据集下的决策图对比图

图10 在R15数据集下的聚类结果对比图
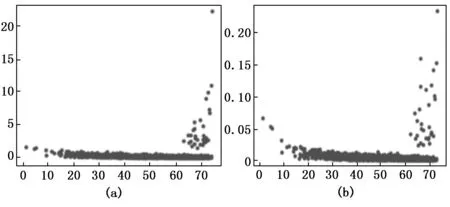
图11 在D31数据集下的相对距离/密度对比图
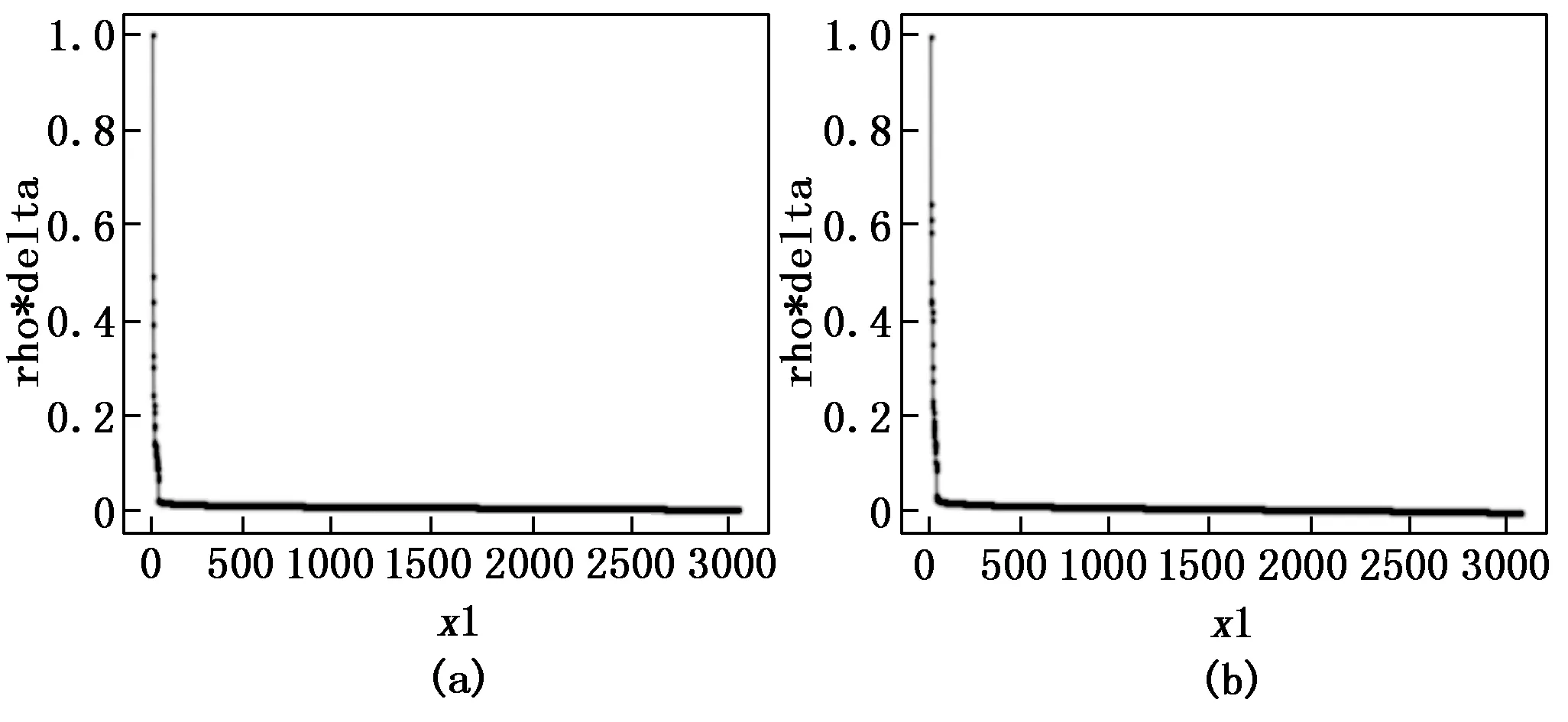
图12 在D31数据集下的决策图对比图
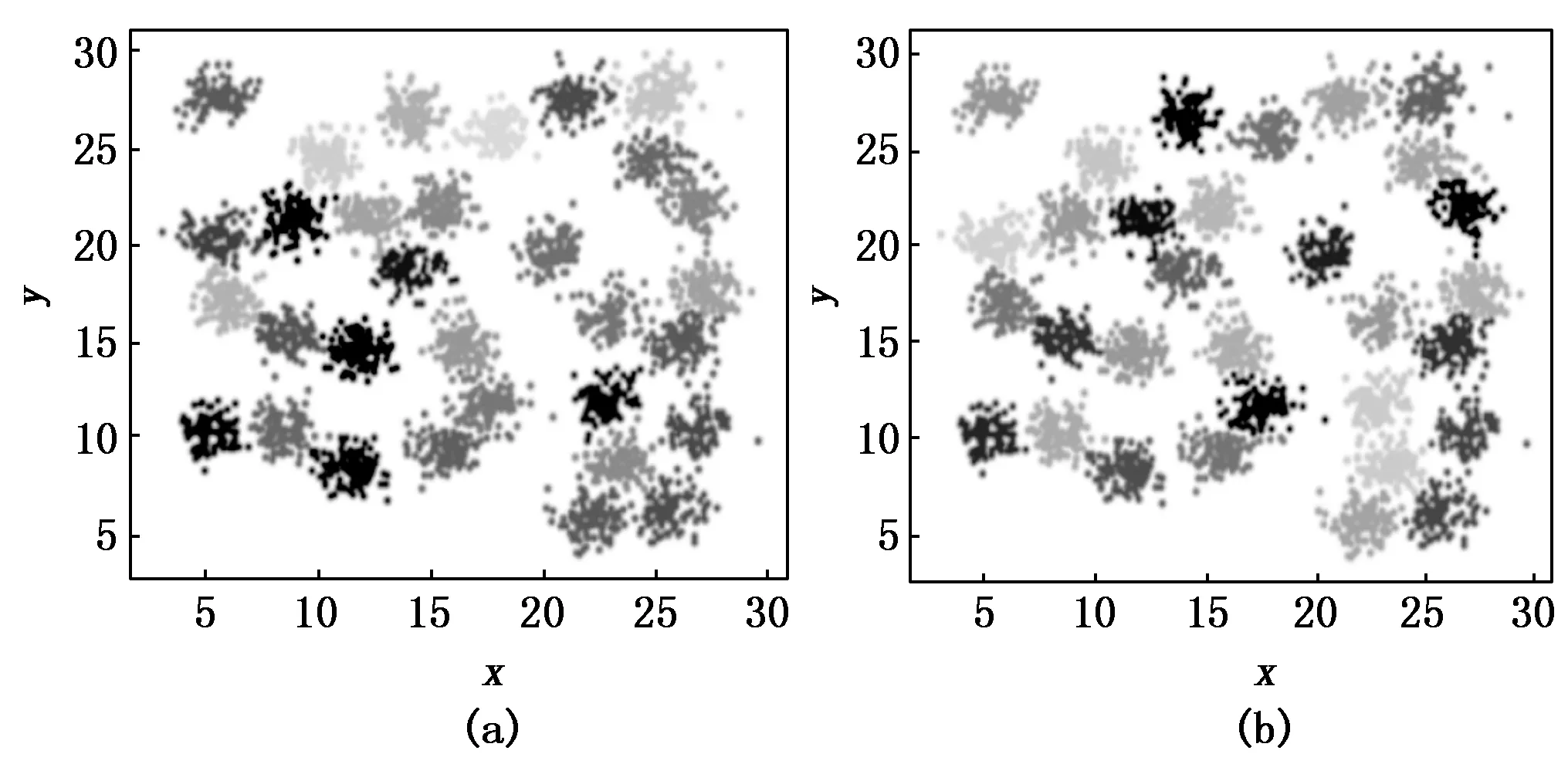
图13 在D31数据集下的聚类结果对比图
以上实验说明数据集在LDDPC算法处理过相对距离δ之后在不影响DPC算法本身效果的同时还使得在决策图上寻找聚类中心时更加容易。
5.5 实验三:高维数据集测试
为了进一步验证算法的有效性,实验三中选取了UCI数据集中的3个高维数据集分别为Iris,Wine,Seed进行测试,实验选用的数据集详细信息如表2,DPC与LDDPC算法实验结果的对比如表3。

表2 实验三所用数据集
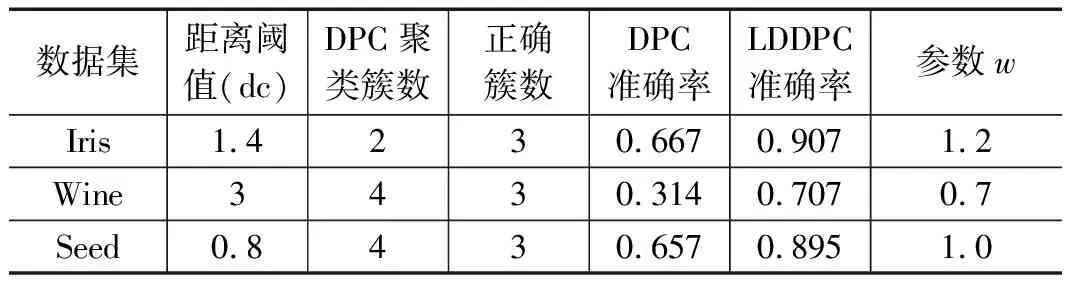
表3 实验三实验结果
实验三在dc值的选择上仍然选择了一个小于1%,一个大于2%,一个介于1%~2%之间且分类错误的3个具有代表性的dc值。在图14中可以看到(a)图被误分成了2类,而(b)图中决策图上出现了3个γe值相对大的点,通过对相对距离进行的加权找到了隐藏的真实聚类中心,即一共3个正确的聚类中心;而图15(a),图16(a)图中被多分成了4类的情况下,经过LDDPC算法处理之后明显看到决策图上γe值相对大的点由4个变为3个,即通过对相对距离的加权使同一簇中原有的两个密度峰值减少为一个,排除了错误的聚类中心,数据集成功地被重新分成了正确的3类,测试效果表明算法在DPC分类错误时能够使分类正确,且可以明显提升算法的准确率。

图14 在Iris数据集下的决策图对比图

图15 在Wine数据集下的决策图对比图
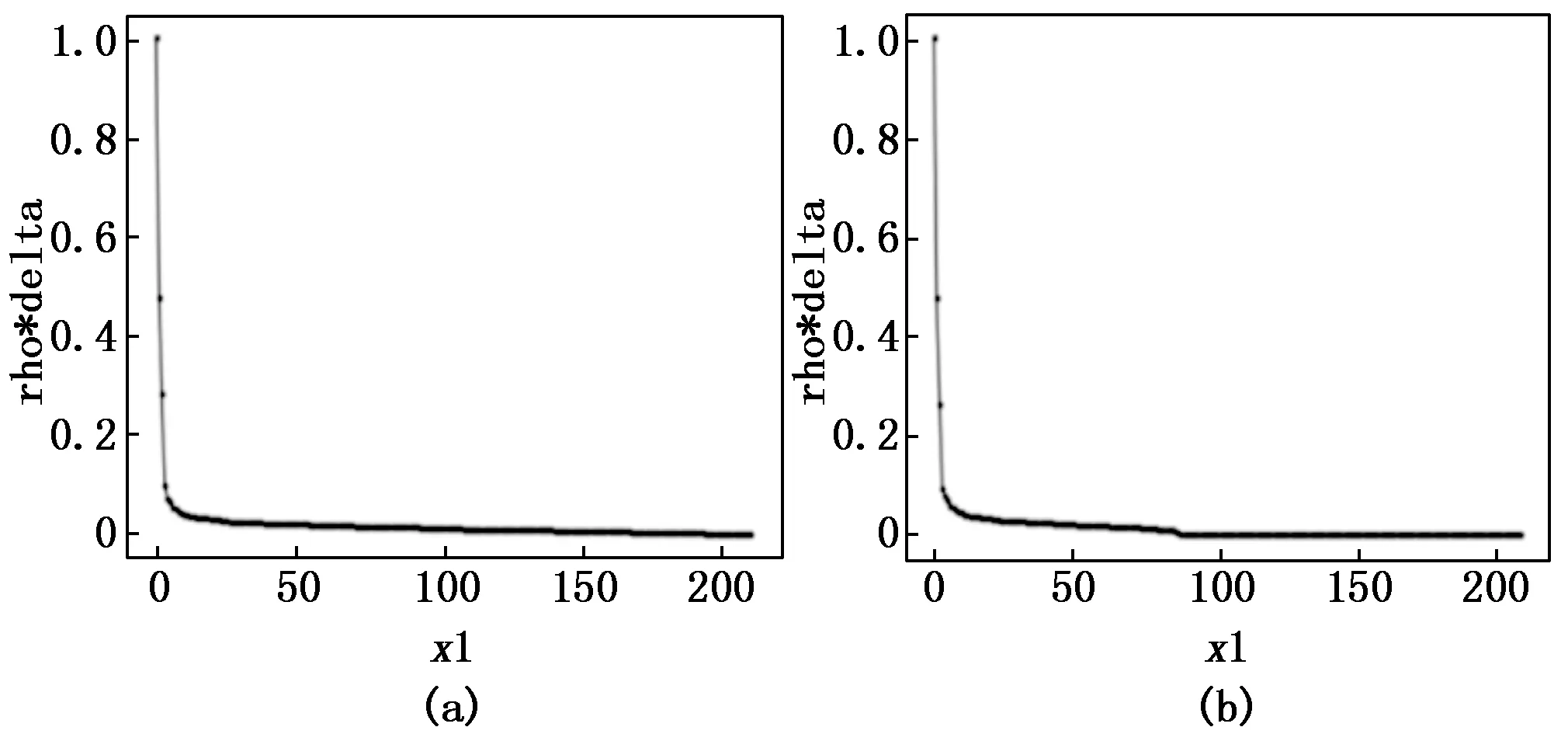
图16 在Seed数据集下的决策图对比图
6 结束语
针对传统的DPC算法在距离阈值选取不当时无法正确分类的情况,本文提出了局部密度捕获范围和利用局部密度信息熵均值的加权算法(LDDPC),成功在距离阈值使分类错误的情况下通过对数据点的相对距离进行其局部密度信息熵均值的加权使分类正确。该算法克服了DPC算法对距离阈值取值敏感的缺点,在数据集上的实验结果可以证明,通过LDDPC算法在DPC算法的距离阈值取值不当导致分类错误时,得以正确分类,并且提高准确率。

