基于双充电状态的锂离子电池健康状态估计
卢地华, 陈自强
(上海交通大学 海洋工程国家重点实验室;高新船舶与深海开发装备协同创新中心,上海 200240)
近些年来,随着全球环保意识的增强,新能源交通运输工具受到行业推崇[1].锂离子电池凭借着其优越的性能特点在交通和储能领域备受青睐,其中,电动船舶和电动汽车都是当下的热点研究领域.锂离子电池健康状态估计是电池管理系统中的一个关键问题,精确的健康状态估计可以掌握电池的衰减情况,实时了解电池模组中单体的不一致性,及时对失效阈值的电池进行更换处理,调整电池的成组情况,使电池组处于最佳充放电状态[2].
锂离子电池健康状态直接在线估计要求测得电池容量、内阻等反映电池老化的表征因素,对于实时运行的锂离子电池系统来说,获取上述数据十分困难[3-4].考虑到在线估计健康状态的重要性,基于可实时获取的电流、电压及温度等数据进行锂离子电池健康状态估计的方法在近些年的研究中逐渐被采用.文献[5]采用放电过程中相同时间下的电压降作为特征预估电池的健康状态.文献[6]利用放电过程中的平均放电压降映射电池健康状态的衰减.文献[7]提出了以放电过程中电压样本熵为特征参数联合智能学习算法的锂电池健康状态估计方法.文献[8]考虑用放电过程中的电压取样熵的变化趋势建立衰减模型并用于健康状态估计,虽然上述方法在特定运行工况下有着较好的估计效果,但是考虑到使用者的不同使用习惯及电池所处的不同环境,导致放电过程中的工况变化不定,数值数据具有较大的不确定性.文献[9]利用容量增量分析法提取恒流充电过程中的峰值高度和峰值位置电压作为特征参数进行锂离子电池的健康状态估计.文献[10]利用电池充电至某电压搁置10 min内的端电压压降信息提取健康因子,映射电池的衰减情况.文献[11]利用老化循环后电池平均欧姆内阻增加量作为特征因子进行健康状态估计.上述方法从充电状态中提取的健康因子都局限于单充电状态下,提取的内阻因子要基于特定的测试,对于恒压充电阶段的因素考虑较少,但是电池充电起始点及截止点因使用情况而异,导致所建模型泛化能力弱.
针对上述问题,本文提出一种基于双充电状态因子的锂离子电池健康状态估计方法.搭建实验台架进行电池老化实验,考虑到实际应用中充电起始点及截止点存在不确定性,在恒流充电阶段末端提取等幅值电压充电时间序列,恒压充电阶段前端提取等时间差电流平均值序列构建健康因子,通过实验数据及理论推导证明所提因子与健康状态存在强关联性,建立改进支持向量回归模型,利用粒子群优化算法寻找模型的最佳超参数,通过检测充电阶段双因子值完成锂离子电池健康状态的在线估计.本文研究可为嵌入式电池管理系统开发提供重要借鉴.
1 锂离子电池老化实验
1.1 电池选型
考虑到电池的老化特性,结合近年来国内研发的三元镍钴锰酸锂电池热稳定性优于钴酸锂电池,质量比能量高于磷酸铁锂电池与锰酸锂电池等因素,本文选取8块额定容量为10 A·h的三元镍钴锰酸锂电池作为实验电池,其额定电压为3.7 V,上截止电压为4.2 V,下截止电压为3 V,质量为 200 g,几何尺寸为130 mm×95 mm×8 mm,实验电池如图1所示.

图1 实验电池Fig.1 Experimental battery
1.2 实验台架
为保证电池实验条件的一致性及数据采集的可靠性,需搭建锂离子电池老化测试台架,台架装置主要包括保证环境温度的实验恒温箱、进行容量精确标定的型号为CT-4008T-5V6A-164的电池单体测试装置、辅助通道(AUX)、进行老化循环的动力电池检测系统、结果可视化及存储的上位机,实验台架布置如图2所示.

图2 锂离子电池老化实验台架Fig.2 Lithium-ion battery aging experiment bench
1.3 实验方案
为获取可靠完整的电池老化数据,本实验采用8个三元镍钴锰电池进行老化测试;满电状态下电池容量标定采用0.5C(C为电流倍率,即电池充放电电流大小与电池额定容量的比率关系),电流放电至3 V,以3次标定的平均值作为电池的容量,具体标定步骤如下所示.
步骤1搁置5 min.
步骤2恒流0.5C充电至4.2 V.
步骤3恒压4.2 V充电至电流0.02C.
步骤4搁置5 min.
步骤5恒流0.5C放电至3 V.
步骤6重复步骤1~5共3次,取容量平均值.
每两次容量标定之间的充电采用恒流恒压充电模式(0.5C恒流充电至上截止电压4.2 V,之后恒压充电至电流为0.02C截止)充满电池,从而获取电池完整充电曲线,以3次充电曲线平均值作为当前老化状态的标准恒流恒压充电曲线;利用电池循环充放电设备进行老化实验,具体步骤为以1C的电流放电至3 V,然后恒流恒压模式充电至4.2 V,如此循环往复,每隔30次循环进行1次电池的容量精确标定及充电曲线的完整获取,具体老化实验的充放电步骤如下所示.
步骤1搁置5 min.
步骤2恒流0.5C充电至4.2 V.
步骤3恒压4.2 V充电至电流0.02C.
步骤4搁置5 min.
步骤5恒流1C放电至3 V.
步骤6重复步骤1~5共30次.
2 健康因子的构建
2.1 电池健康状态的定义
健康状态也称为寿命状态(SOH),本文主要考虑电池容量与健康因子间的对应关系,故采用电池容量定义电池的健康状态.从电池容量的方面定义如下:
(1)
式中:SSOH为健康状态;CM为测量容量;CN为电池标称容量.
2.2 健康因子的提取
在电动交通工具的使用过程中,电池都是处于放电状态的,并且由于使用者的不同使用习惯及外界多变的环境条件导致电池的放电状态是一个无规律的过程,从中提取健康因子相对比较困难,精度不高且泛化能力弱.而电池的充电状态是比较固定的模式(恒流恒压充电),因此考虑从充电曲线中提取健康因子可靠性强[12-14].电池放电终止状态的不一致性可能导致电池的不完全放电,使得恒流充电的起始点发生较大改变,因此考虑从恒流充电的末端提取健康因子.同样鉴于电池充电结束状态的不一致性,可能导致电池的不完全充电,继而使恒压充电的终止端发生较大改变,因此考虑从恒压充电的前端提取健康因子.
由文献[15]可知,恒流充电阶段的等幅值电压充电时间和电池老化有着密切的相关性,因此考虑提取恒流阶段末端的等幅值电压(3.75~4.2 V)充电时间作为第1个健康因子.考虑到恒压充电阶段主要是电流在发生变化,从恒压充电阶段前端提取健康因子势必要考虑电流变化和电池老化的关系[16],故需建立合适的模型.
n阶阻容(RC)模型可以较准确地模拟电池的极化特性,串联的RC网络越多,模型的精度越好,但建模所需的参数大量增加,鉴于本文考虑恒压充电阶段的电流与老化关系分析,所以选用其中经典的Thevenin模型进行分析,模型结构如图3所示.其中:Uoc为开路电压;Ul为内部阻抗分压;Ut为电池端电压;RS为欧姆电阻;RD为极化电阻;CD为极化电容;UD为极化电压;IB为干路电流;IC为电容电流.
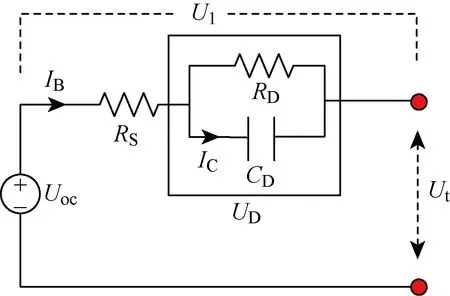
图3 1阶RC等效电路模型Fig.3 First-order RC equivalent circuit model
Thevenin模型的动态响应方程如下所示:
(2)
Ut=Uoc-UD-RSIB
(3)
可将式(2)和(3)写成离散形式:
UD(k+1)=UD(k)e-Ts/τ+
IB(k)RD(1-e-Ts/τ)
(4)
Ut(k)=IB(k)RS+UD(k)
(5)
式中:k为第k个采样时刻;Ts为采样周期时间;τ为时间常数,其值等于RDCD.将上式进行Z变换,其脉冲响应变换传递函数为
(6)
(7)
式中:a0、a1、a2分别为式(6)中的对应系数.由于采样周期Ts可以看成一个趋近于0的数,则有:a0=RS,a1≈-RS,a2≈-1.
则电压电流离散关系可以写为
Ul(k+1)=a0IB(k+1)+a1IB(k)-a2Ul(k)
(8)
联立可得:
Uoc(k+1)-Ut(k+1)=a0IB(k+1)+
a1IB(k)-a2(Uoc(k)-Ut(k))
(9)
可得电流的表达式为
(10)
考虑到现在分析的是恒压充电阶段,因此电压恒定,则有:
(11)
由式(11)可知,要得到准确的电流值必须获取准确的开路电压值.由于开路电压与荷电状态(SOC)有着很好的对应关系[17-18],所以得到二者的模型关系后即可由SOC值得到对应的开路电压(OCV)值.考虑到不同老化程度下的OCV-SOC对应关系存在不确定性,本文在不同老化程度下采用静置法进行OCV-SOC测试,结果如图4所示,其中:SSOC为电池当前的荷电状态.图5则为不同老化程度下恒压充电电流实验结果,其中:t为当前时刻;I为该时刻下的电流值.

图5 不同老化程度下恒压充电电流实验结果Fig.5 Experimental results of constant voltage charging current in different aging degrees
由图4可知,不同老化程度下电池的OCV-SOC关系可能会存在差异,但是差异主要体现在70%SOC以下区域,对于高SOC区域,OCV-SOC关系基本稳定,差异性小并且趋近于线性关系[19].对于恒流恒压充电模式而言,恒流充电阶段承担了绝大部分的容量充给,恒压充电只占相当小的一部分,所以恒压充电阶段的电池处于高SOC状态.考虑到上文研究的为恒压阶段的推导,因此可以建立OCV-SOC(70%以上)的线性模型关系式如下:

图4 不同老化程度下OCV-SOC实验结果Fig.4 OCV-SOC correspondence in different aging degrees
Uoc(k)=dSSOC(k)+f
(12)
式中:d、f分别为线性模型的斜率和截距,则上述电流关系可写为
IB(k)=IB(k-1)+
(13)
将SOC关系式带入,可得:
(14)

(15)
考虑恒压充电阶段的电流特性,初始点为恒压充电起始点,其电流值IB(0)为恒流阶段的电流值,对应老化实验中的0.5C,即5 A.将离散形式连续化,由于恒压充电时间t′=kTs,则上式可写为
(16)
IB(t)=h0IB(0)
(17)
式中:h0为式(16)中的初始电流系数.由于RS对应着电池的欧姆内阻,随着电池的老化加剧,RS不断增大,对应式(17)的系数值h0也不断增大,对应的相同时间下的电流值也增大;由以上推导可知,恒压阶段相同时间内的电流平均值必然和电池容量变化存在着负相关的关系.图5的结果展示了电池不同老化程度下恒压充电阶段电流的变化情况,以恒压阶段开始为时间起点,由实验可知老化程度越高,相同时间点的电流值越大,8个电池实验结果均与推导关系相符,故选取恒压阶段前端等时间差电流平均值作为第2个健康因子.
为进一步证明所提取的相关健康因子满足估计要求,本文使用了美国国家航空航天局卓越预测中心的公开数据集中2A·h的18650型电池进行相关性分析,本文选用B5、B6、B7、B18号电池进行验证;选取恒压充电初始阶段 1 500 s的电流平均值为第1个健康因子H1、恒流充电阶段(3.75~ 4.2 V)的充电时间为第2个健康因子H2及相应循环的容量值进行相关性分析,相关结果如表1所示.

表1 健康因子与容量相关性Tab.1 Health factors and volume correlations
由表1可知,本文采用的两个健康因子H1、H2均与电池容量具有强关联性[20],所以采用二者进行健康状态估计是合理的.
3 基于双充电因子的电池健康状态估计
3.1 支持向量回归模型
支持向量回归(SVR)模型是基于支持向量机(SVM)引出的模型,可用于数据的预测估计,具体流程如图6所示.其中:下标i为第i个;上标“∧”为估计值;X为健康因子序列;M为健康因子映射标签值序列;r为间隔距离;L为拉格朗日函数;lε(z)为不敏感损失函数;ξ为松弛因子;ε为偏差系数;μ为拉格朗日系数.SVM可概括为寻找一个超平面wTx+b=0,wT为超平面的法向量,x为输入向量;b为截距.将数据按标签yi值进行区分,使离该面最近样本点到决策面的距离最大化;考虑选定的电池健康因子及容量样本数据集,为了解决健康状态估计方面的问题,在SVM的基础上引入正则化因子(惩罚因子)E0,得到电池健康状态估计的支持向量回归模型,并引入核函数及拉格朗日乘子Δ进行求解.

图6 支持向量回归流程图Fig.6 Flow chart of support vector regression
3.2 粒子群优化算法
对于建立的支持向量回归模型,存在部分参数需要确定,惩罚因子E0及核函数参数g是主要需确定的两个参数;考虑到本文针对的是锂离子电池健康状态估计,样本数据采样周期密集导致选取的健康因子维度较大,容量存在局部回弹变化性,传统的网格搜索方法无法定位较大范围;传统的遗传算法(GA)部分参数(如交叉率、变异率)的选择大多依靠经验,对初始种群的选择具有依赖性,对容量的跟踪记忆性随种群的改变被破坏;而粒子群优化(PSO)算法不必遍历网格中所有的参数点来确定优解,且具有良好的记忆性,对于好解粒子都将保存,所以本文采用其进行参数寻优,具体如图7所示.

图7 粒子群模型参数寻优流程图Fig.7 Optimization process of particle swarm model parameters
初始化粒子群后,更新粒子的速度和位置,相关公式为
(18)
(19)

3.3 双充电健康因子估计结果
为验证所提方法的泛用性,本文采用美国国家航空航天局卓越预测中心的公开数据集中2A·h的18650型B5、B6、B7号电池前110个循环,B18号电池前90个循环进行模型训练,B5、B6、B7号电池后57个循环,B18号电池后41个循环作为测试集对模型精度进行校验;为验证所建估计模型的精确度,将其与传统遗传算法优化GA_SVR和PSO_SVR进行比较,对比结果如图8所示.其中:CBAT为电池的容量;n为实验老化循环的次数.

图8 两种优化算法估计结果Fig.8 Results of two optimization algorithm estimations

(20)
(21)
式中:nRA、nMA为2种评价指标对应的样本数.RMSE及MAPE的值越小,证明模型的精度越高,两种优化算法下的预测结果如表2所示.

表2 不同优化算法的预测结果Tab.2 Forecast results of different optimization algorithms
由表2可知,双充电状态健康因子联立PSO_SVR模型的估计方法既可以很好地反映电池容量的全局变化趋势特性,也可以很好地通过健康因子追踪容量局部回弹变化的不稳定性,具备较强的泛化能力及回弹变化感知能力.相较于GA_SVR策略,所提出的PSO_SVR方法电池健康状态估计误差小,跟踪优势更加明显.为进一步证明模型的泛化能力,联立上述估计方法,采用不同电池的数据结合估计.在B5号电池基础上联合B6、B7、B18号电池样本数据为训练集,B5号电池部分样本数据作为验证集进行测试.在B6号基础上联合B5、B7、B18号电池样本数据作为训练集,B6号电池部分样本数据作为验证集进行测试.结果如图9所示.

图9 电池组合数据估计结果Fig.9 Estimated results of battery combination data
由图9可知,所建立的PSO_SVR模型能够很好地追踪B5、B6号电池的衰减特性,表明所提健康因子在同类电池中具有相似表征,能够间接对同类电池进行精确健康状态估计;所建立的PSO_SVR模型估计结果的MAPE分别为 0.016 8、0.024,优于 GA_SVR 的 0.020 6、0.038 8;RMSE为 0.032 5、0.055 5,优于 GA_SVR 的 0.041 1、0.072 7;结果证明了基于双充电状态健康因子的PSO_SVR模型的适应性及有效性.
4 结语
本文针对锂离子电池健康状态估计实际应用中存在不完全充放电而导致的充电起始点及截止点不确定问题,提取恒压充电阶段前端的电流平均值及恒流充电阶段末端的等幅值电压充电时间作为健康因子,通过理论推导及老化实验证明了所提因子与健康状态的强关联性,其中Person系数绝对值均不低于 0.992 7,Spearman系数绝对值均不低于 0.991 3.构建的基于双充电状态因子的PSO_SVR模型能够很好地追踪电池老化趋势,具备容量回弹变化性的表征能力,可通过监测当前循环下的健康因子值在线估计电池健康状态,其单体估计结果的RMSE值均不超过 0.015 1,MAPE值均不超过 0.020 5,电池的组合数据估计结果的RMSE均不超过 0.055 5,MAPE值均不超过0.024,优于传统的GA_SVR模型.相较于传统的单充电状态因子估计,所提的基于双充电状态因子的锂离子电池健康状态估计方法适用性广,可靠性强.

