基于双域变换的鲁棒可逆信息隐藏算法研究

摘 要：以鲁棒可逆水印为研究对象，分别基于图像空域、整数小波域设计隐藏方案，利用图像分块技术划分圆心面和矩形子块，并嵌入鲁棒水印，保障在有损传输环境中水印的抗攻击能力;采用直方图平移技术嵌入脆弱信息，解决图像溢出等边信息问题，保证无损传输环境下图像的可逆性。试验结果表明，在同等可嵌入量的条件下，本方案在多类型图像攻击环境中，水印的鲁棒性、图像的视觉效果优于其他同类方案。

关键词：图像双域;鲁棒水印;可逆脆弱信息;直方图平移

中图分类号：TP309     文献标志码：A     文章编号：1003-5168（2022）3-0006-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.03.001

Study of Robust-Reversible Data Hiding Algorithm Based on Image Dual-Domain Transformation

YU Shuang

（Jiangsu Vocational Institute of Commerce， Nanjing 211168，China）

Abstract：Taking robust reversible watermarks as the research object， a novel information hiding scheme based on spatial and transform domain is proposed. Image blocking technology is used to divide the host image into a circle and sub-blocks for embedding robust watermarks under lossy environment. The side information such as overflow coordinate， which is hidden as fragile information by histogram shifting， can ensure the reversibility of host under non-destructive condition. It turns out that， the robustness and visual quality are superior to others with the same capacity of watermarks in different image attack environment.

Keywords： image dual-domain; robust watermarking; reversible data hiding; histogram shifting

0 引言

鲁棒可逆信息隐藏技术充分考虑载体图像在不同环境中传输的差异性。当图像在嵌入信息后经历诸如压缩、几何攻击等篡改后，可以提取出具有鲁棒性的水印。而图像未遭受其他修改或攻击时，除了可以提取鲁棒水印，还能复原载体至初始状态。比较经典的是Ni[1]提出的空域划分子块的方法：首先，将若干不重叠子块投射至直方图中，选取一个直方图特征统计量，然后，利用相邻像素的初始相似性，修改一侧像素点的灰度值，使得统计量发生改变，通过这种变化体现鲁棒水印的嵌入。后续学者诸如李晓波[2]、于爽[3]等多基于空域直方图平移技术设计方案。与空域方案不同，Coltuc[4]基于图像离散余弦度换（Discrete Cosine Transform，DCT），将鲁棒水印隐藏于变换域系数中，变换域中图像能量集中，鲁棒性更强，可抵抗较高强度的图像压缩。缺点是像素值采用了浮点型变化，嵌入水印后，产生大量的边信息。为了隐藏边信息，图像需要大幅变动，可视性差。此外，已提出的方案多针对图像压缩处理，较少涉及图像旋转等几何攻击。对此，本研究创新性地提出基于空域、变换域的双域隐藏算法，在空域选取圆心面嵌入对抗几何攻击的鲁棒水印，在变换域利用整数小波变换嵌入对抗图像压缩的鲁棒水印。该方案产生的边信息较少，可与像素值（下文简称灰度值）溢出位置一起隐藏于脆弱信息之中。嵌入信息后，图像视觉效果良好。

1 基于双域的鲁棒水印嵌入

1.1 雙域子块划分

首先在载体图像中心处截取一个圆面，圆面中包含偶数个像素点，如图1所示。然后将圆面划分成等量的两组，“+”位置像素点为子集S1，“-”位置像素点为子集S2。

将圆心面以外的图像区域进一步划分成若干不重叠的子块，每一子块大小为8×8。利用整数5-3小波将每一子块进行2阶变换，并投射至变换域中，如图2所示。

1.2 鲁棒水印嵌入

在圆心面中，选择S、S两个子集灰度值的算术平均差作为特征统计量α，计算公式如式（1）。

初始状态下，S、S两个子集中的像素位置相邻，灰度值近似，统计量α趋于0，满足Laplace分布。引入变化量δ，让S1子集中所有像素的灰度值都加上δ，使得统计量绝对值|α|远离零点。在遭受图像攻击时，远离零点的特性仍能较好保持。就此实现圆心面1 bit鲁棒水印的嵌入。

如图2所示，进入图像剩余矩形子块的整数小波域。小波域属于一种图像频域，在频域中，图像能量高度集中于低频系数段LL子段。低频子段具有高鲁棒性，但轻微的变动会急剧降低图像的视觉质量;右下角高频子段HH对原始载体干扰小，但鲁棒性差。结合上述特性，在每一子块完成2阶整数小波变换后，观察中低频子段HL2和LH2中坐标为（1，3）与（3，1）的系数c、c。初始状态下两个系数包含的能量相似，在此引入系数差值统计量β（β=c-c）以及正值增量γ，通过公式（3）扩大系数差值，实现1 bit鲁棒水印的嵌入。系数值的正负性代表嵌入的信息是0或1，水印的嵌入可容量等于矩形子块的数量。

至此，基于空域圆心面和小波域中低频系数段分别实现了若干鲁棒水印的隐藏。

2 边信息与溢出问题

2.1 边信息的产生

在信息隐藏过程中往往会产生大量的边信息，现有的一些方案需要通过额外的传输通道将其发送给接收方，以保证信息能够被提取。多次传输增加了信息传递的风险，非真正意义上的盲提取。本方案在圆心面嵌入阶段，只产生了变化量δ、半径R的边信息;在小波域嵌入阶段则产生了中低频系数交换位置、系数增量γ等边信息。与其他方案[1-4]相比，边信息量极少，可以与下文2.2节像素值溢出位置一起作为脆弱信息隐藏于图像直方图中。

2.2 像素值溢出问题

由第1节可知，信息在隐藏过程中会对图像的灰度值进行改动。空域中直接修改灰度值，小波域则修改频域系数。当图像从频域反变换回空域时，系数变化也会引发灰度值的变化。图像灰度值的取值范围为0～255，0代表全黑，255代表全白，其余灰度值则表示从黑至白的不同色阶。当原始像素的灰度值接近极值0或255时，引入的变化量δ和γ会引发灰度值翻转，从而产生图像噪声。

可采用灰度值截断的方式：当像素点灰度值变换后低于0或超过255时，控制溢出点的灰度值在0或255处。超出的变化量予以记录，与溢出点位置一起作为边信息隐藏于脆弱信息中。截断公式如式（3）所示，其中G（x，y）为原始灰度值，G'（x，y）为截断后的灰度值，（x，y）为像素点的空域坐标。

2.3 脆弱信息的隐藏

本研究边信息产生量少，可以利用图像中高频出现的灰度级p实现边信息的隐藏。如图3所示，首先将灰度级高于p的像素点灰度值全部加1，灰度级255通过试嵌入的方式记录为溢出信息，空出p+1的bin。将信息0隐藏于p级，信息1隐藏于p+1级。隐藏前灰度值为p的像素点的个数即为脆弱信息的可嵌入量。此外，还可以通过增加p点的方式扩大隐藏容量。

3 信息提取与无损恢复

信息提取的步骤与嵌入阶段的步骤互逆，分为在有损环境和無损环境下操作。当隐藏信息的载体图像在传输过程中遭受旋转等几何攻击时，圈出如图1所示的圆心面，并划分左右子集，依据公式（1）计算出两个子集的算数平均值差|α'|。若|α'|超过一定阈值，则代表鲁棒水印提取成功;若载体经历了图像压缩处理，首先提取圆心面鲁棒水印。然后，依图2所示，将剩余矩形子块投射至整数小波域中，计算两个中低频系数差值。若差值为正，提取鲁棒水印1;若差值为负，提取鲁棒水印0。

在无损环境下，载体图像未经历任何篡改及攻击。将图像投射至直方图后，逐一扫描像素点并读取灰度值。若灰度值为p，提取脆弱信息0;若灰度值为p+1，提取脆弱信息1，并将灰度值恢复为p。其余大于p+1的像素点则全部将灰度值减去1，恢复图像至隐藏脆弱信息前的状态。然后，提取出所有鲁棒水印，利用获得的脆弱信息即边信息，根据公式（3）、公式（2）逆序复原图像至原始状态，实现无损环境下的可逆性。

4 试验结果

本方案选取如图4所示的六幅经典灰度图像Lena、Elaine、Baboon、Airplane、House及Lake作为隐藏水印的原始载体。这六幅图像的粗糙度、直方图分布各异，极具代表性。通过测试在不同传输环境中，接收端在不同载体中提取出水印的鲁棒性、不可见性以及多方案对比来检测本方案的性能。

4.1 鲁棒性和不可见性测试结果

4.1.1 JPEG压缩环境下测试结果。当载体经历JPEG压缩处理后，在接收端提取出所有矩形子块以及圆心面的鲁棒水印，与原始鲁棒水印进行比对。压缩因子越小，代表压缩强度越高。

试验结果如表1所示，鲁棒水印嵌入量为4 093 bits，变化量δ=20、γ=18。当图像在压缩因子为60的高强度压缩下，鲁棒水印的提取准确率仍可达86%以上，并可通过BCH纠错码实现完全纠错;当压缩因子在75以上时，鲁棒水印提取准确率高达99%以上，满足了水印鲁棒性要求。

图5以House图像为例，以其边界特征作为鲁棒水印，并回嵌至原始载体图像，展示了在不同强度的图像压缩下，提取水印的准确率。由图5可知，压缩强度越高，鲁棒水印信号越易丢失，反之则不然。

4.1.2 旋转攻击环境下测试结果。在旋转攻击下，主要测试圆心面的1 bit水印能否提取成功。表2展示了水印抵抗不同旋转角度的能力。角度在20°以内，所有载体图像中的鲁棒水印均可以准确提出。随着旋转角度的增强，左右子集像素逐渐插值趋同，抗旋转性也逐步降低。但20°以内的抗攻击力在现有同类盲提取方案中仍属优越。

4.1.3 不可见性测试结果。为了测试图像嵌入信息后的视觉效果，即水印不可见性，采用图像峰值信噪比（PSNR）作为衡量指标。表1、表2最后一列显示了在嵌入信息后，5幅图像的峰值信噪比达到了30 dB以上。Baboon原始图像分布粗糙，轻微的像素修改易造成图像信号的丢失，所以峰值信噪比略低。总体上满足了一般性试验要求。

4.2 对比试验结果

与空域方法Ni[1]以及变换域Coltuc[4]进行比对，以本方案性能较弱的House图像为载体，测试在相同嵌入量的前提下，水印抵抗压缩和旋转攻击的鲁棒性。

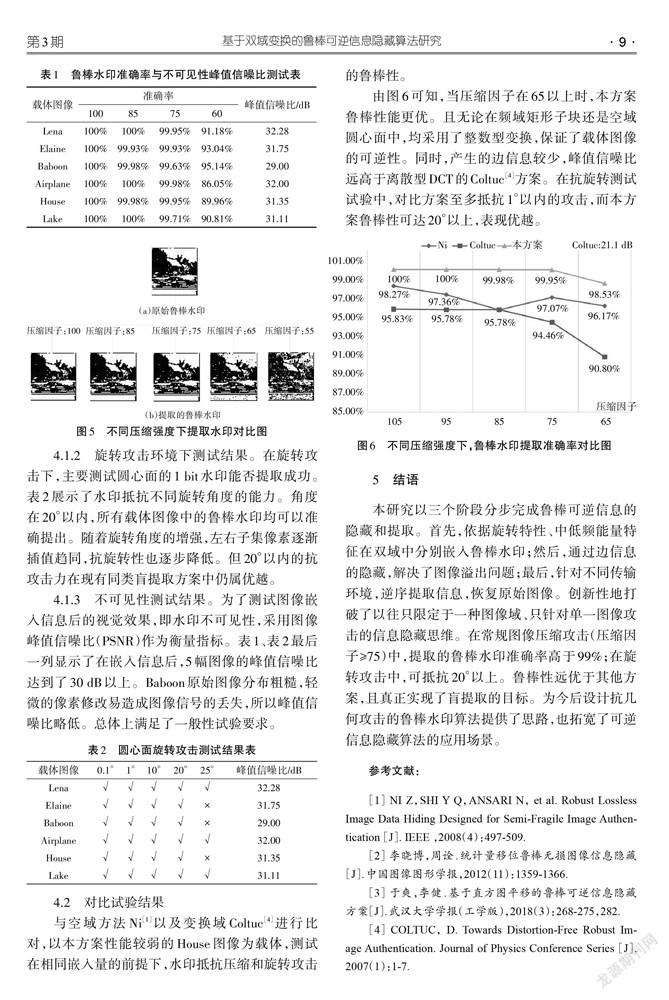
由图6可知，当压缩因子在65以上时，本方案鲁棒性能更优。且无论在频域矩形子块还是空域圆心面中，均采用了整数型变换，保证了载体图像的可逆性。同时，产生的边信息较少，峰值信噪比远高于离散型DCT的Coltuc[4]方案。在抗旋转测试试验中，对比方案至多抵抗1°以内的攻击，而本方案鲁棒性可达20°以上，表现优越。

5 结语

本研究以三个阶段分步完成鲁棒可逆信息的隐藏和提取。首先，依据旋转特性、中低频能量特征在双域中分别嵌入鲁棒水印;然后，通过边信息的隐藏，解决了图像溢出问题;最后，针对不同传输环境，逆序提取信息，恢复原始图像。创新性地打破了以往只限定于一种图像域、只针对单一图像攻击的信息隐藏思维。在常规图像压缩攻击（压缩因子≥75）中，提取的鲁棒水印准确率高于99%;在旋转攻击中，可抵抗20°以上。鲁棒性远优于其他方案，且真正实现了盲提取的目标。为今后设计抗几何攻击的鲁棒水印算法提供了思路，也拓宽了可逆信息隐藏算法的应用场景。

参考文献：

[1] NI Z，SHI Y Q，ANSARI N， et al. Robust Lossless Image Data Hiding Designed for Semi-Fragile Image Authentication [J]. IEEE ，2008（4）：497-509.

[2] 李晓博，周诠.统计量移位鲁棒无损图像信息隐藏[J].中国图像图形学报，2012（11）：1359-1366.

[3] 于爽，李健.基于直方图平移的鲁棒可逆信息隐藏方案[J].武汉大学学报（工学版），2018（3）：268-275，282.