基于Dirichlet-to-Neumann映射计算波导中缺陷激发的连续谱束缚态*
陆明鑫, 胡真
(河海大学 理学院,江苏 南京211100)
1 引言
在正能量的连续域内可以存在孤立解,即局域模式的能量落在连续体内,这种嵌模不与扩展波耦合,具有无限的寿命,就像零宽度的谐振[1],量子力学中将这种状态称为连续域束缚态(Bound states in the continuum),简称BIC.最近,人们认识到BIC本质上是一种波动现象,在光学上,由于其无限高质量因子(Q因子)和对系统参数变化的鲁棒性,使其在生物传感[2-4]和开关[5]以及非线性光学[6]等方面上有很多应用.目前,BIC在光学领域中的研究已经取得了很大进展[7-8].
在众多存在BIC的材料中,光子晶体[9]因其设计简单和易于制作而备受关注.当在光子晶体波导中引入两个对称的点缺陷时,由于缺陷之间的相互作用,可以用两能级模型[10]的近似结构来描述它们的耦合机制.通过调节缺陷的结构参数,使强烈的共振干扰将共振态与连续体的耦合完全抑制,这时便激发出了BIC.
分析与计算光子晶体波导中的BIC需要高效的数值方法.求解光子晶体波导中由缺陷激发的BIC,等价于求解缺陷的实共振频率,而这是一个腔膜问题,因此可以作为麦克斯韦方程的特征值问题来求解.传统的数值方法,如有限差分法[11-12]、有限元法和平面波展开法[13]等,求解时都会产生大矩阵特征值问题,因此求解比较困难.此外,对于色散介质,矩阵项依赖于频率,特征值问题会变得非线性,将更加难以求解.
2006年Huang等[14]提出了一种特殊的频域方法——Dirichlet-to-Neumann (DtN)映射方法,可以用来精确模拟二维光子晶体器件.DtN映射方法通过将边界上的波场映射为边界上对应的法向导数,以避免对计算区域内部的计算,将原来的特征值问题变成一个小矩阵线性特征值问题,其中特征值是Bloch波矢量,ω是一个给定参数,这种方法降低了计算的工作量和难度.目前,DtN映射方法已经被广泛应用于分析各类光子晶体结构[15-18].
本文将DtN映射方法应用于二维光子晶体波导中由缺陷激发的BIC的计算与分析,其主要思想便是利用严格的边界条件截断波导管,从而得到一个有限的计算区域,再通过单元晶格的DtN映射进一步将计算域缩小到在单元晶格上的所有边上,最终在边界上建立起求解小矩阵的特征值问题.基于该方法,便能确定激发波导中BIC的点缺陷的半径和介电常数范围.
2 DtN映射方法
在二维光子晶体波导中引入两个对称的点缺陷为谐振腔,可以激发出BIC,以点缺陷平行于波导排列的结构(图1(a))为例,进行DtN映射方法构建.该结构是一个由空气中的介质棒按正方形晶格排列的光子晶体,其晶格常数为L,介质棒半径r,介电常数为ε,背景空气折射率为n.其中黑色填充圆表示波导中具有可变介电常数εd的附加局部缺陷棒,可以引起左右波导中传播模式的散射,从而激发出BIC.
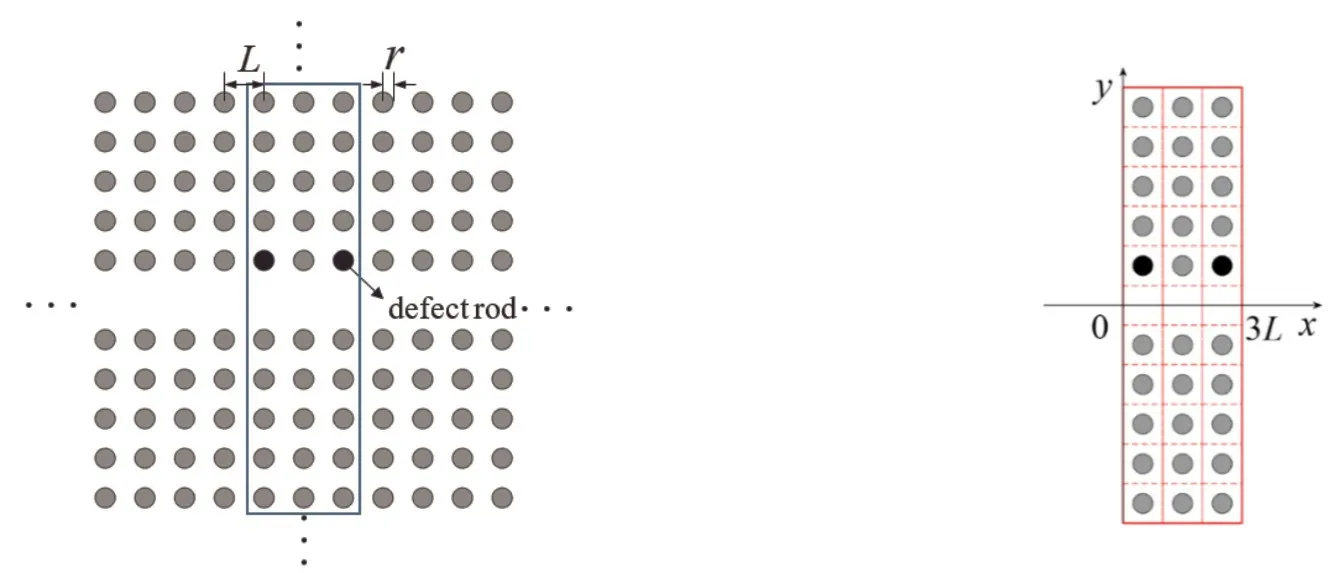
(a)完整二维光子晶体波导 (b)截断区域
对于在z方向上不变,且波在xy方向上传播的二维问题,E-偏振下,控制方程为
(1)
其中,k0=w/c是自由空间波数;w是角频率;c是真空中的光速;n(x,y)是折射率函数;u是在E-偏振下方向z上的电场分量(唯一非零分量).
考虑上述结构,缺陷晶格放置在了光子晶体波导附近.因此,为了计算缺陷模式,对附近波导建立精确的入射和出射的边界条件尤其重要.本文通过使用严格的边界条件来截断PhC波导,将计算域截断为图1(b)所示矩形S,假设计算域由0 (2) (3) 其中L+和L-是两个作用于y上的算子,它们依赖于给定的频率,并且当对y进行离散时,便可以用矩阵逼近. (a)单元晶格 (b)超级晶格 确定了截断PhC波导的边界条件后,将计算域划分为正方形晶格并计算DtN映射[14].对于如图2(a)所示,若每边离散N个点,DtN映射Λ可近似为一个4N×4N的矩阵,即 (4) 一般来说,边界上每条边上的点在选取上都会避开顶点进行均匀选择. 在建立了单元晶格的DtN映射后,对于计算域中内部的边,可以利用两个相邻单元晶格的DtN映射来匹配∂vu;在计算域边界的边上,则使用一个单元的DtN映射和严格的边界条件即(2),(3)来匹配∂vu.最终在单元晶格的边上,得到了一个这样的线性方程组 A(ω)U=0, (5) 其中,U是计算域S中所有边上u的列向量;A是依赖于ω的矩阵.以图1为例,若计算域是p行q列的单元晶格组成的,则总边数m=2pq+p+q,那么U是一个mN×1的列向量,A是一个mN×mN的方阵. 结构的共振频率ω需要通过求解方程(5)的非零解来得到,当A是一个奇异矩阵时,可以使用非线性方程 λ1(A(ω,r,ε))=0 (6) 来迭代求解根ω.其中,λ1是A(ω)的特征值的绝对值中最小的特征值.当固定半径r时,对于公式(6),需要求解出对应于实频率ω的一组解(ω,ε).这是因为BIC是有着完美的局域性且没有能量泄露,而复频率ω表示为ω=ω0-iγ,其中虚部则表示能量泄露,故判断BIC的条件是γ=0. 对于固定半径r,以缺陷晶格的介电常数ε为变量,当找到对应于实频率模式的共振模,便找到了BIC.因此,当以半径为变量,对范围内的每个半径值,只要能找到对应于实频率ω的解,便有了一组能够激发BIC的点缺陷参数对(r,ε),如此就确定了能够激发波导中BIC的点缺陷的半径和介电常数范围. 以图1(b)为例,讨论x=3L右侧的半无限光子晶体波导的边界条件,对于波导的一个周期xj (7) 其中,uj和∂xuj是xj处的电场值及其法向导数;M是一个2mN×2mN的矩阵. 基于算子M,可以计算波导的Bloch模,对于周期性的结构,波导中的波场是Bloch模的叠加,一个Bloch模就是方程(1)的一个特解,即 φ(x,y)=Φ(x,y)eiβx, (8) 其中Φ在x上关于L具有周期性,β是常数.因此对于μ=eiβL来说,有 φj+1=μφj,∂xφj+1=μ∂xφj, (9) 因此Bloch模可以通过特征值方程 (10) 求解;其中,特征值μ=eiβL,φ和∂xφ为xj处的值,I是单位矩阵.通过利用Bloch模,可以将光子晶体中微腔的波场展开为 (11) 当频率ω为复频率时,条件|μ|≤1并不总是有效的,因为此时原本在实频率下随x的增加而衰减的模也会随着x的增加而增长,故需要进行修正.由于BIC的共振频率的虚部通常是非常小的,对于这样的复频率ω,它的Bloch模的特征值与它对应实部的频率的Bloch模的特征值非常接近,因此修正的方法是计算并筛选复频率ω实部所对应的Bloch 模来作为复频率所对应的Bloch模[18]. 基于方程(11)的Bloch模展开,有 (12) 其中,φk=Φk(xj,y),μk=eiβkL,因此可以定义算子T使得 Tφk=μkφk,k=1,2,…. 由于T是线性的,则有uj+1=Tuj,且由(7)中给出的DtN算子M可以得到 ∂xuj=L+uj,其中L+=M11+M12T. (13) 通过同样的方法,也可以得到左边界上的L-算子.综上,得到了终止PhC波导的严格边界条件. 本节计算了几种结构算例[20]中能够激发BIC的点缺陷的结构参数范围. 第一个算例如图1所示,计算区域为3×15个正方形单元晶格.利用本文方法,以点缺陷半径rd为变量,得出当rd在[0.056,0.5]范围内变化时,都可以找到一个介电常数εd,使得结构中出现BIC,如图3所示.取参考文献中的半径rd=0.18L,得到εd=3.035 8,wL/2πc=0.374 3,这与文献[19]中的结果一致,该点电场图如图3中右侧所示. 图3 图1所示结构εd与rd的关系图和rd=0.18L时电场图 第二个算例如图4(a)所示,计算区域为5×15个正方形单元晶格.利用本文方法,以点缺陷半径rd为变量,得出当rd在[0.044,0.5]和[0.127,0.5]范围内变化时,都可以找到一个介电常数εd,使得结构中分别出现了奇BIC和偶BIC,如图4(b)和4(c)所示.取参考文献中的半径rd=0.18L,分别在εd=1.990 9,wL/2πc=0.374 1激发出了奇BIC,以及εd=5.615 2,wL/2πc=0.327 3时激发出了偶BIC,结果与参考文献[19]中的结果一致,其中这两个BIC的电场图如图4(b)和4(c)中插图所示. (a) 缺陷平行波导结构图 (b) 奇BIC的εd与rd关系图 (c) 偶BIC的εd与rd关系图 算例三是一个缺陷相对于坐标x→-x,y→-y反对称排列的结构,如图5(a)所示.这里将计算区域截断为3×15个正方形单元晶格.利用本文方法,以点缺陷半径rd为变量,得出当rd在[0.051,0.5]范围内变化时,都可以找到一个介电常数εd,使得结构中出现BIC,如图5(a)所示.取参考文献中的半径rd=0.18L,得到εd=2.517 9,wL/2πc=0.374 2,这与参考文献[19]中的结果一致,其中这点电场图如图5(b)中插图所示. (a)缺陷反对称排列结构图 (b) εd与rd的关系图 将DtN映射方法应用于二维光子晶体波导中BIC的计算与分析,确定了在光子晶体波导中能够激发波导中BIC的点缺陷的结构参数.本文的方法使得不需要在整个平面上进行计算,而只需要在截断区域内计算,而即便在较小的计算域中,也只需要在单元晶格的边界上进行离散,而不需要考虑晶格内部,从而最终在单元晶格边界上建立起小规模的特征值问题,降低了计算量和难度.本文只是对理想的二维结构进行计算分析,下一步考虑将这种方法扩展到三维的结构上去,研究三维波导管中的连续谱束缚态.
3 边界条件

4 数值算例
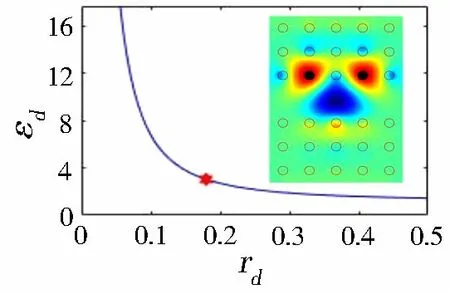
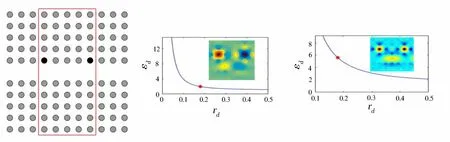

5 结语

