基于特征融合的单幅图像超分辨率重构方法

陈 平

(徽商职业学院，安徽 合肥 230000)

0 引 言

图像是一种直接获得的可视化信息，人们可以通过图像获取和利用对自己有价值的信息。随着社会的发展，各行各业对图像质量的要求也越来越高，例如交通部门的电子监控系统、医学和天文学领域等。数字图像是由数字设备如摄像机、数码相机、录像机等电子设备生成的图像[1]。然而在实际生活中，经常会因为环境或设备本身原因造成图像质量的降低[2]。因此提高图像的分辨率在实际应用中具有很大意义。

为了获得高分辨率的图像，最直接的方法是改进或更换硬件设备，但成本较高。因此图像超分辨率重构(super resolution,SR)技术已成为解决这一问题的主要途径[3]。

在计算机视觉中，SR是具有很大的吸引力和挑战性的任务，目的是从一幅或多幅低分辨率图像中生成详细的和空间分辨率强的图像。通常SR可以分为3类:基于插值的方法、基于重构的方法和基于学习的方法[4-5]。基于插值的方法简单、快速，但结果过于平滑，振铃现象严重。基于重建的方法利用数学模型重建高分辨率图像，但计算复杂。基于学习的方法充分利用了图像固有的先验知识。该方法能很好地保留图像的细节，适用于处理特殊图像，如光谱图像[6]、红外图像[7]和医学图像[8]。但是基于学习的方法需要大量的训练样本，训练的时间代价也很高。

本文提出了一种新的图像超分辨率算法，即特征融合卷积超分辨率重构神经网络(FFSRN)。该方法由3个部分组成，第一部分是提取LR图像的特征，第二部分是将提取到的各个层次LR图像的特征传递到深层并融合，第三部分是重构HR图像。本文的内容组织如下：在第一节中，对所提出的SR方法进行了详细的说明，第二节给出了实验结果，第三节对本文进行了总结。

1 本文方法

1.1 GoogLeNet卷积神经网络

现在卷积神经网络越来越大，性能也越来越好。在一般情况下，神经网络的性能可以通过增加层数和每层滤波器的数目来提高[9]。GoogLeNet是2014年ImageNet的冠军，它的体系结构被认为是网络中的网络[10-11]。主模块称为Inception架构，是一个很小的网络，在该网络中，对图像同时进行不同大小的滤波器卷积，得到不同的特征图，然后将这些特征图连接在一起，形成新的融合特征图。该结构减少了滤波器大小对神经网络性能的影响，可以提取更多的特征。因此GoogLeNet有非常好的表现。该方法受Inception架构的启发，在第一层使用不同的滤波器大小来提取更多的特征，提高图像的重建性能[12-13]。

1.2 特征融合超分辨率重构网络

特征融合超分辨率重构网络(FFSRN)是LR图像与对应的HR图像之间的端到端的映射。FFSRN实验验证了通过调整网络的层数、滤波器的大小和每层滤波器的数目可以影响重构结果。因此本文将使用3种不同的滤波器尺寸，同时对LR图像进行处理，然后将不同的特征图连接起来共同形成新的融合特征图，可以提高图像重建的质量，如图1所示。

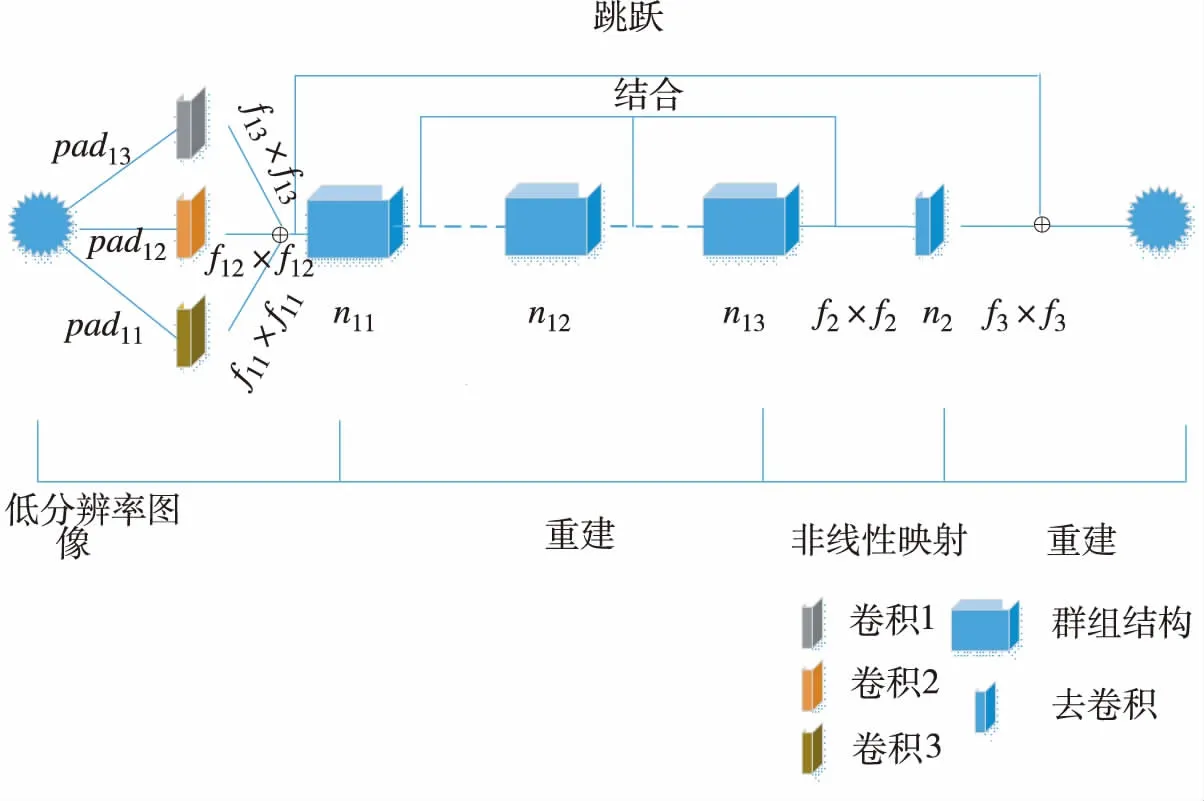
图1 特征融合超分辨率重构网络结构

在接下来的叙述中，X代表高分辨率图像，Y为双三次低分辨率图像插值，X和Y大小，尺寸相同。F(Y)表示为图像的重构,F(Y)与X最相似。

1)特征提取

在第一层中，图像同时被3层包含卷积不同尺寸卷积层的滤波器f11,f12和f13进行特征提取(对应的分别是pad11,pad12，pad13)。这3个特征图相互关联共同形成新的一层融合特征图，作为下一层的输入。特征提取与表示为

F1(Y)=max(0,W11*Y+B11)
⊕max(0,W12*Y+B12)
⊕max(0,W13*Y+B13)

(1)

其中，f11×f11，f12×f12，f13×f13为滤波器尺寸，W11，W12，W13为滤波器权值，B11，B12，B13为滤波器偏值，n11，n12,n13滤波器的个数 和B11，B12，B13为n维空间向量，假设n11=n12=n13=n1，其中‘*’表示卷积操作，‘⊕’表示连接符。

2)非线性映射

非线性映射是指将1个三维图像特征映射到2个n维特征。非线性映射表示为

F2(Y)=max(0,W2*F1(Y)+B2)

(2)

其中，f2×f2是滤波器的大小，n2是滤波器的数目。其中W2和B2分别是滤波器的权重和滤波器的偏置。二维矢量表示n2维高分辨率特征并被用于最终的重建。

3)图像重建

从重构滤波器卷积n2维高分辨率特征中得到最终的HR图像。图像重建表示为

F(Y)=W3*F2(Y)+B3

(3)

其中，W3是对应于f3×f3滤波器的滤波器权重，B3是标量。

1.3 损失函数

超分辨率重构算法一般习惯使用均方误差(mean squared error，MSE)作为损失函数来测试训练模型的精度和更新模型的参数。所以在本文中，我们仍然使用MSE作为损失函数来训练神经网络，表达式为

(4)

其中n是训练图像的数量，Yi是采用双三次插值的第i个低分辨率图像，Xi是低分辨率图像对应的高分辨率图像，F(Yi;Θ)由网络模型Θ重建高分辨率图像。

2 实 验

2.1 实验数据和特征融合卷积超分辨率重构网络模型结果

本文采用DIV2K数据集。数据集1包括96幅图像，训练集为91幅，测试集为5幅(Set5)(图2)。数据集2包括986幅图像，训练集为976幅，测试集为10幅(Set10)，其中5幅与Set5相同。

本实验分别使用Dataset1和Dataset2训练FFSRN模型。用FFSRN模型、FFSRN Dataset1模型、FFSRN Dataset2模型对Set5进行测试(图2)。注意FFSRN模型是由ImageNet进行训练的，因此只能得到最终的重建结果。

图2 FFSRN网络实验结果

图3和图4为实验在训练和测试时所得的PSNR和SSIM指标，网络训练迭代次数为1 000次，PSNR值可达38.5，SSIM值可达0.955。此外实验表明训练数据越多，网络的性能越好。并且，对于图像重建，自然图像集优于合成数据集。

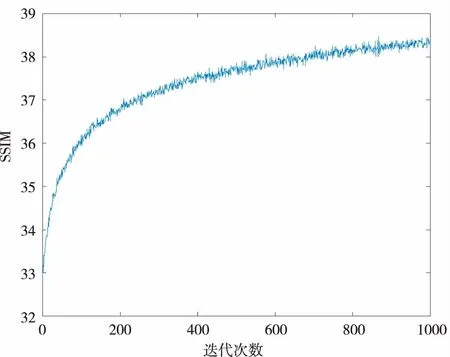
图3 训练集的PSNR指标

图4 训练集的SSIM指标

2.2 损失函数的收敛性分析

下图5和图6分别为Dataset1和Dataset2数据集训练时的损失函数收敛图。由图可知，1 000次迭代已接近收敛，损失函数的收敛情况相似。

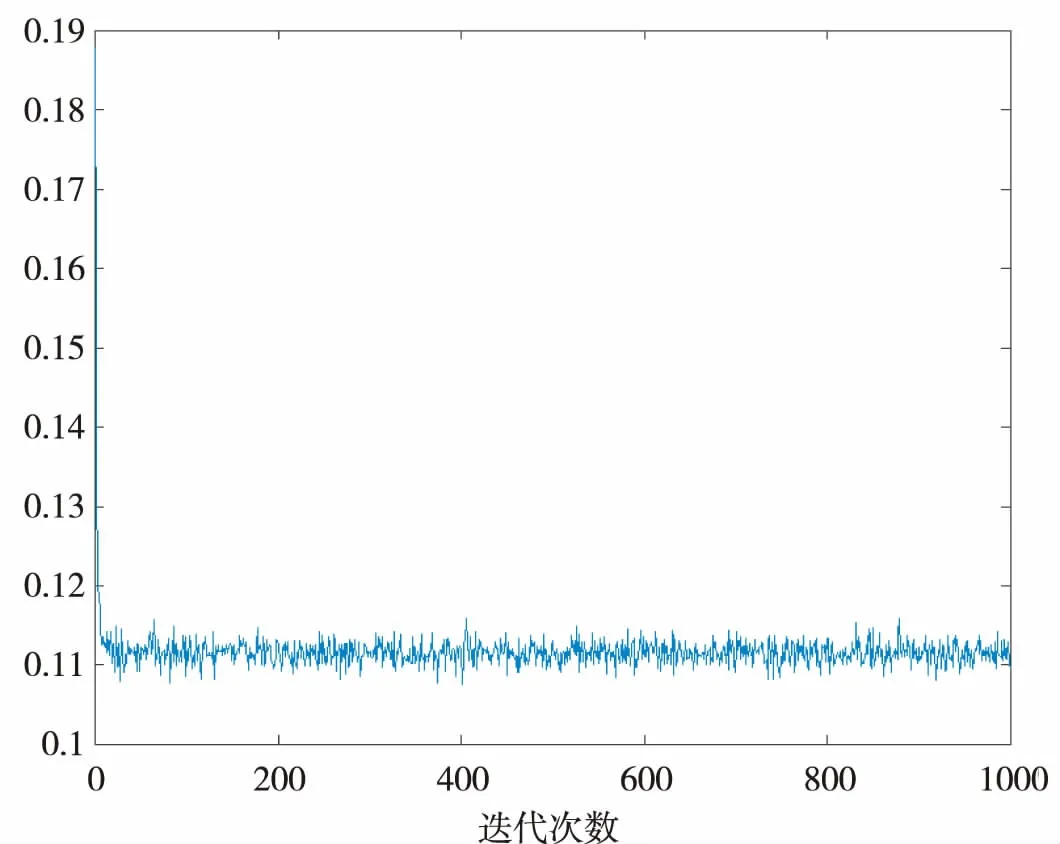
图5 Dataset1 MSE收敛曲线

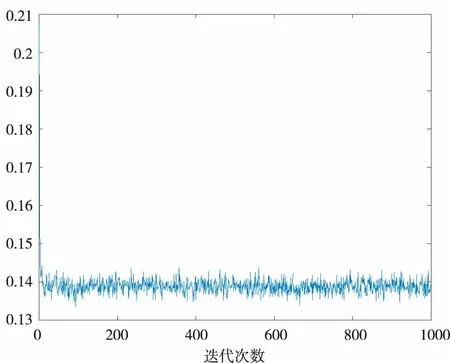
图6 Dataset2 MSE收敛曲线图

2.3 FFSRN网络参数

为了提高图像的重建质量，在第一层设计了3种不同的滤波器尺寸，特征融合卷积超分辨率重构网络。FFSRN1：

(f11=5,f12=7,f13=9,f2=3,f3=5;

n11=n12=n13=32,n2=32,n3=1);

FFSRN2：

(f11=7,f12=9,f13=11,f2=3,f3=5;

n11=n12=n13=32,n2=32,n3=1);

FFSRN3：

(f11=9,f12=11,f13=13,f2=3,f3=5;

n11=n12=n13=32,n2=32,n3=1)。

2.4 模型参数

1)滤波器的数量

在FFSRN2中，每层的过滤数为n11=n12=n13=32,n2=32,n3=1。本实验改变了第一层和第二层的过滤数，即FFSRN4和FFSRN5。

2)滤波器的尺寸

在FFSRN2中，非线性映射层的滤波器大小为f2=3。将非线性映射层的滤波器大小调整为FFSRN6(f2=1)和FFSRN7(f2=5)。在训练集上的测试结果如实验表明，FFSRN2的平均PSNR值高于其他两种模型，因此FFSRN2模型仍然是最佳选择。

3 结 论

本文提出了一种自然图像超分辨率重建方法。基于FFSRN网络算法，该方法在第一层卷积过程中使用多尺度并行滤波器，以获得更多的图像特征。在第二层实现非线性映射，然后在第三层进行超分辨率重建。实验表明，该模型能有效提高低分辨率图像的质量，但由于实际的如法医图像、车牌大小等图像通常很小，甚至只有十几个像素，因此，实验结果不是很理想。所以在后续工作中将研究高倍化重建方法。