基于梯形压电悬臂梁的折线形结构振动能量采集装置
王志豪,王丽坤,,廖擎玮
(1.北京信息科技大学 仪器科学与光电工程学院,北京 100192;2.北京信息科技大学 传感器北京市重点实验室,北京 100192)
0 引言
便携式电子设备及无线传感网络近几十年得到快速发展,尤其在野外传感网络系统、人体健康监测系统、环境控制系统、嵌入式系统、军事安全应用系统等领域得到广泛应用。对这些设备的传统供电方式有电池供电等。相对于微型传感器来说,电池体积较大,限制了系统的进一步小型化;此外,其能量供应寿命有限,使用一段时间后需要充电或更换,造成人力和物力的浪费[1]。而环境能量采集装置可以将生活中广泛存在的自然能源转换为有用的电能,成为长期甚至无限生命周期的自主供电系统[2]。
随着基于压电材料的振动能量采集装置研究的广泛展开,出现了结构多样的压电发电装置,如悬臂梁单晶/双晶结构[3]、Cymbal结构[4]、叠堆形结构[5]等,其中矩形悬臂梁是最成熟的结构[6]。国内外学者开展了很多有关矩形截面压电悬臂梁结构的优化设计研究工作。Mateu等[7]分析了矩形和三角形压电悬臂梁结构,当三角形与矩形悬臂梁固定端相等且三角形高度与矩形长度相同时,相同激励力下三角形压电悬臂梁能产生更大的应变,故能提高效率。但是这种结构在悬臂梁的长度方向上无法使应力分布均匀化,因此不能最大程度地利用压电材料[8]。此后,Roundy等[9]提出梯形截面压电悬臂梁结构能有效地提升能量采集效率;Baker等[10]开展了相关的试验研究,制作了等体积的矩形和梯形压电悬臂梁,试验结果表明,梯形悬臂梁相比矩形悬臂梁能量采集效率提升了30%。进一步研究发现,梯形悬臂的应变分布比矩形悬臂更均匀,但仍不够理想[11-12]。
本文提出了一种基于传统梯形双悬臂梁的新型振动微能量采集装置,它采用折线形结构,利用该结构的转动惯量可以进一步改善梯形悬臂梁的应变分布。
1 结构和模型
本装置的整体结构和每个组成部分的精确尺寸如图1所示。该装置由一个普通的梯形悬臂梁和折线形结构复合组成。梯形悬臂梁由钢衬底和基于PZT-5的压电层组成。折线型结构包含两个由两条铝合金条连接的金属块。
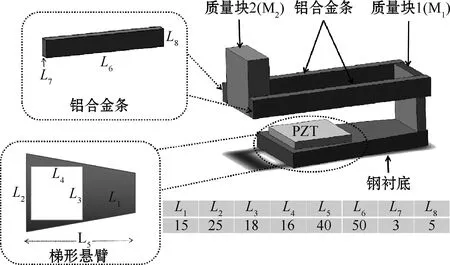
图1 装置整体结构和各组成部分尺寸(单位为mm)
该结构可以建模为分段线性振动冲击装置,如图2所示。
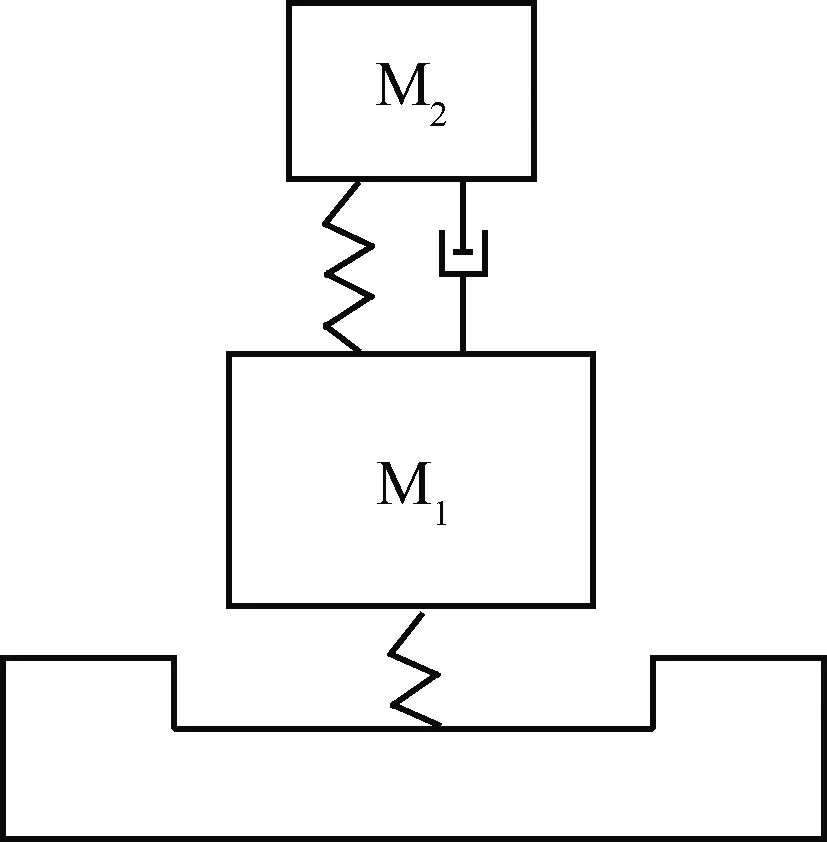
图2 能量采集装置的等效机械模型
系统运动方程如下:
(1)
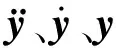
|K-ω2M|=0
(2)
由式(2)可得系统的一阶谐振频率ω1与二阶谐振频率ω2。系统的主要模态φ1和φ2可由ω1和ω2确定。采用振型叠加法求解系统动态响应,位移y的表达式为
y=φ1q1+φ2q2
(3)
其中q为每种振动模态所占的比例大小,是时间的函数。当一阶共振频率与二阶共振频率相近时,系统振动位移是一阶振型与二阶振型的线性叠加,从而拓宽共振频率,产生二次冲击,并传递到二次弹簧质量系统(能量采集元件)。然后次级质量块M2以其自身的共振频率振动,该频率高于主弹簧—质量系统的频率,并呈指数衰减。由于次级质量块M2较大的转动惯量而产生的较大位移,其冲击增加了压电层上的平均应力,导致输出电压或功率与带有动态放大器的传统俘能器相比有所增加。
该结构有多种振动模态。本文主要研究了第一振动模态和第二振动模态,如图3所示。
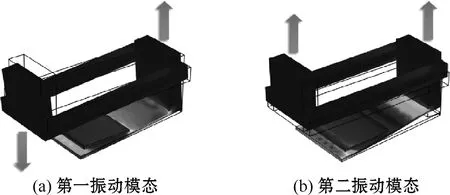
图3 振动模态
从图3可以看出,在第一模态中,两金属块在相反的方向上远离,而在第二模态中,两金属块在相同的方向上移动。这两种模态都可以使应变分布更加均匀。显然,第二模态的输出功率高于第一模态。在结构上施加一个振动激励时,悬臂梁的加速度a(t)=ag×sin(2πf0t),其中:ag=1.0g;f0=160 Hz。
应用Comsol Multiphysics软件进行有限元模拟,做出该结构的等效机械模型,仿真结果如图4所示。
通过该模型发现,控制分离质量块的质量比,折线形结构可以在梯形悬臂梁的自由端产生交变的弯矩。当质量比改变时,输出电压也发生变化。图4(a)显示了不同振动频率下质量比从0.2到2.0的输出电压。当振动频率为132 Hz和339 Hz,质量比为1.2时,输出电压分别可以达到10.33 V和34.18 V。
通过仿真可获得梯形悬臂梁基板表面的应力数据。为了对比,同时模拟一个在自由端附着质量块的传统梯形悬臂梁。两种结构中涉及的压电陶瓷和基板的材料、尺寸等参数都是相同的。图4(b)为两种结构沿悬臂梁伸长方向上的应力分布曲线。从所示曲线可以看出,带折线型结构的应力分布范围明显小于不带该结构的传统梯形悬臂梁。显然,折线型结构可以使应变分布更加均匀。

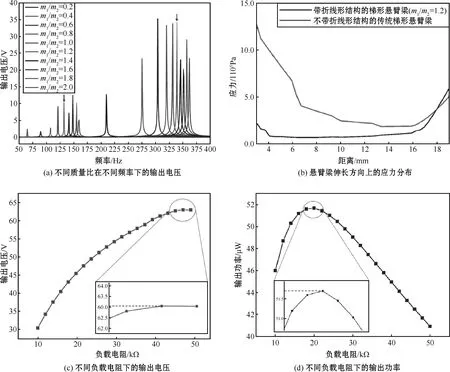
图4 有限元仿真结果
2 实验与讨论
在压电振动能量采集系统的研究中,目前应用最广泛的压电材料为锆钛酸铅(PZT),这是因为其压电性能较高。因此本装置采用的是在实验室用固相法制备的压电陶瓷材料PZT-5。PZT-5的化学式为0.93Pb0.95Sr0.05(Zr0.52Ti0.48)O3-xPb(Mg1/3Nb2/3)O3-(0.07-x)Pb(Ni1/3Nb2/3)O3(x分别为0.01、0.02、0.03和0.05 mol)。材料的具体制备步骤如下:首先将Pb3O4、SrCO3、MgO、NiO、ZrO2、Nb2O5和TiO2这些高纯度(> 99.9%)氧化物粉末用无水乙醇和氧化锆球研磨8 h,再将干燥的粉末在950 ℃煅烧2 h,然后加入8%的聚乙烯醇压制成直径为12 mm、厚度为1 mm的颗粒。最后在1 275 ℃下烧结得到所需样品。
首先对制得样品进行相关性能的测试。图5(a)是压电性能测试结果,当x=0.02 mol时其性能参数为d33=512 pC/N,kp=0.69。图5(b)是X射线衍射(XRD)和扫描电子显微镜(SEM)测试结果。XRD结果表明,PZT-5晶体结构为典型的四方结构;从SEM照片可以看出,x=0.02 mol时的晶粒PZT-5为八面体颗粒。
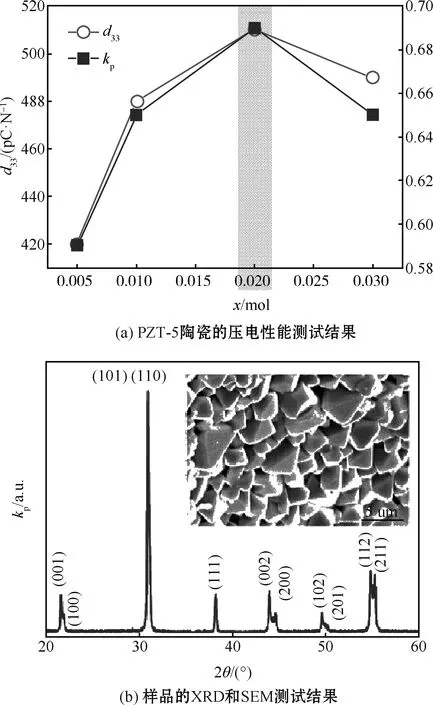
图5 样品性能测试结果
然后对带有折线形结构的悬臂梁进行受力应变分布测试实验,图6是应变测试实物图以及实验结果。在图6(a)中标记的4个点处进行受力分析。图6(b)是在质量块2上施加1.5 N 的压力时的应变分布结果,可以看出此时应变分布是均匀的。应变分布试验结果与有限元分析结果相似,印证了仿真分析结果。
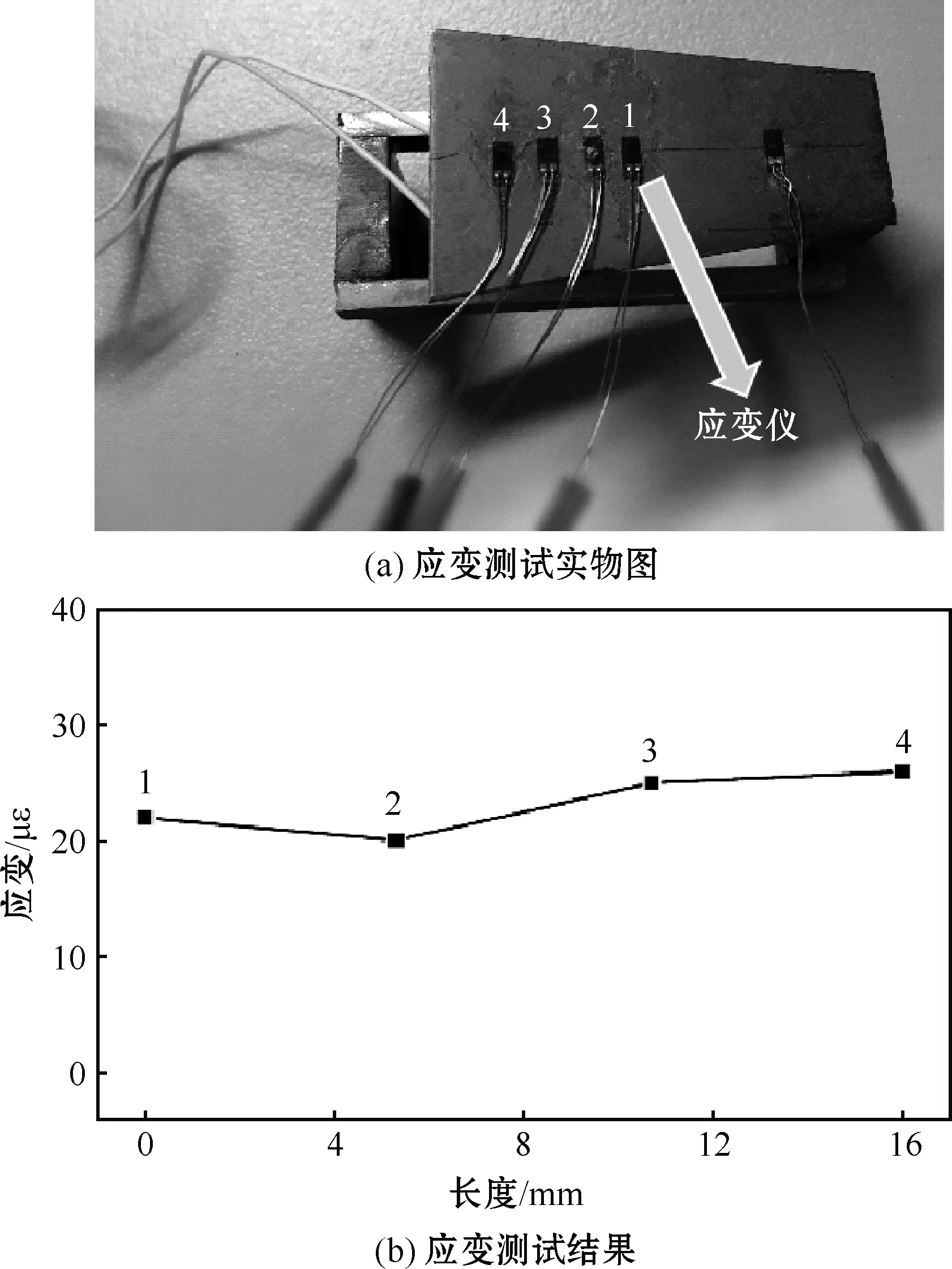
图6 应变分布测试
最后,对折线形结构悬臂梁和传统梯形压电悬臂梁做电压输出对比实验。制作传统梯形压电悬臂梁所用的材料与新结构悬臂梁一致。首先我们测试了没有使用新型结构的传统梯形压电悬臂梁的输出电压。在测试时,给梁体施加一个大小适当的激扰作用力,其频率正好等于梁体的某阶固有频率,则梁体便会产生共振,这时梁体变形即为该阶固有频率所对应的主振型,此时,测出压电悬臂梁的开路电压。不同上下底比率下的梯形压电悬臂梁的输出电压如表1所示。mmass为端部质量块的质量。梯形压电悬臂梁的上下底比值表示为r=L1/L2,其中L1是梯形较窄的底,L2是梯形中较宽的底。当 0 表1 传统梯形压电悬臂梁的输出电压 图7是折线形结构悬臂梁输出测试实验中被测样机的结构与测试系统。将样机放在振动台上,振动台在该结构共振频率的频率范围内以正弦振动运行。通过使用反馈系统,加速度保持在恒定水平(1.0g)。振动筛中的加速度计测量频率和加速度的实际值,并反馈到控制处理器中,然后放大处理后的信号,用以在给定频率下驱动振动器达到所期望的加速度。数字万用表将设备的电输出信号转换成数字信号。 图7 电功率输出测试实验 图8为不同频率下的输出电压。可以看出,当第一模态下的振动频率为189.21 Hz或第二模态下的振动频率为268.04 Hz时,输出电压达到最大值(41 V)。但是当环境激励频率偏离振动能量采集器的固有频率时,输出电压会迅速下降。实验结果与模拟仿真的差异可能是由于制作工艺的偏差,但总体一致。 图8 不同频率的输出电压示意图 本文设计了一种折线形结构的梯形悬臂梁振动能量采集装置,可优化梯形悬臂梁上的应变分布。通过有限元分析和动态应变仪及振动台测试发现:当两质量块的质量比调为m1/m2=1.2时,沿悬臂梁伸长方向的应力分布将变得相当均匀。应变分布与有限元分析结果是吻合的,说明该结构可有效提高压电材料的利用率。 同时,连续振动的实验结果表明,第一模态下的振动频率为189.21 Hz或第二模态下的振动频率为268.04 Hz时,输出电压达到最大值(41 V),高于没有使用折线形结构的传统梯形悬臂梁所输出的最大电压(25.7 V)。因此,这种具有折线结构的新型梯形悬臂梁,可以使梯形悬臂梁的纵向应变分布趋向均匀,并且使得整体结构在不同振动模态下的输出表现更为优秀。 根据以上实验和结论,在今后的研究中,可以从理论上推导出更精确的物理模型,尽可能减小模拟分析结果的误差;应进一步改进和优化基本压电结构,增加频率响应带宽;同时,研发新型高性能压电材料并使之实用化,对于进一步提高其能量输出具有重要意义。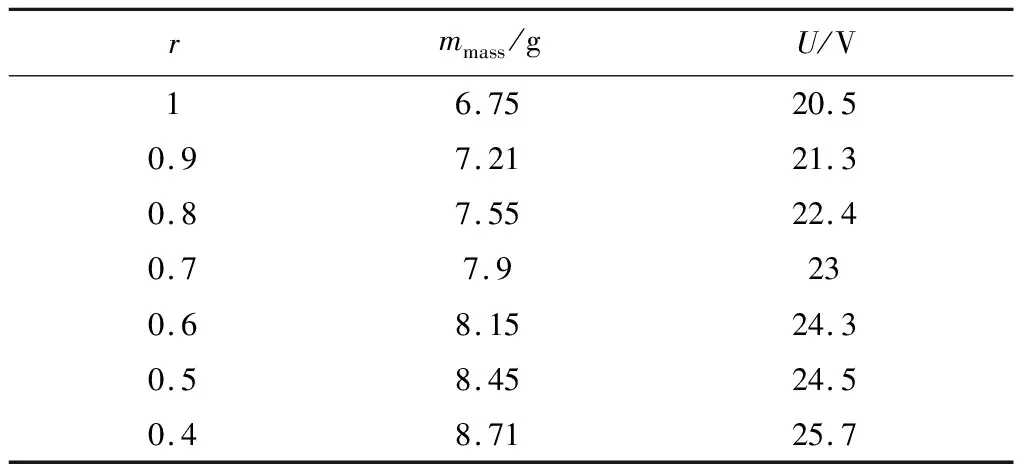


3 结束语

