基于改进萤火虫算法的农产品物流配送路径多目标规划研究

杨 松

(贵州大学 人民武装学院 信息工程系，贵阳 550025)

随着电子商务的发展和物流业的兴起，农产品物流配送效率直接影响企业的物流配送成本和消费者的满意度。为了降低农产品物流配送成本、满足消费者的需求，如何科学地规划和部署农产品物流配送路径成为物流配送企业亟待解决的问题。对于物流配送路径规划问题，很多学者进行了研究。王战权等[1]将遗传算法用于物流配送路径规划，与传统的混合整数规划法相比，遗传算法求解物流配送路径具有更高的搜索效率和更低的配送成本。赵冬玲等[2]提出了一种改进的单点PMX交叉方法求解大规模的物流配送优化模型，结果表明，该算法具有更快的收敛速度和最短配送路程和最低的配送成本。吴兵等[3]提出一种基于优先权编码的遗传算法的物流中心选址优化模型，该方法能够有效降低求解选址问题的复杂度。针对易腐物品的物流中心选址问题，姜大立等[4]提出了一种基于AGA的整数规划的物流中心选址数学模型，结果表明该算法可以增加获得最佳配送路径的概率。

为了降低农产品物流配送成本，提高消费者满意度，实现农产品物流配送路径的合理规划和调度。本文针对萤火虫算法(Firefly Algorithm，FA)存在局部最优和收敛速度慢的缺点，提出一种云自适应萤火虫算法，并将其应用于农产品规划多目标物流配送路径的模型求解。选择物流配送成本最低和路径最短为目标函数，将萤火虫位置编码为车辆编号和车辆路径顺序，通过改进的萤火虫算法规划出农产品多目标物流配送的最佳路径。

1 改进的萤火虫算法

萤火虫算法[5]是基于萤火虫发光的生物特征提出的群智能算法。萤火虫的亮度I、吸引度β、萤火虫之间的距离rij分别定义为：

(1)

萤火虫位置更新数学公式为：

xi(t+1)=xi+β×(xj(t)-xi(t))+α×(rand-1/2)，

(2)

式中：xi(t)、xj(t)表示迭代次数为t时的萤火虫i和j的位置；xi(t+1)表示迭代次数为t+1时的萤火虫i的位置；γ为光强吸收系数；I0和β0分别为萤火虫的最大亮度和最大吸引度；α、rand为扰动。

由于FA算法在后半段极容易出现由于局部最优与全局最优的左右摇摆而导致的局部最优问题，为了解决此问题，运用云模型[6]的随机倾向性和稳定性生产惯性权重引入FA，提出云自适应萤火虫算法(Cloud Model Adaptive Firefly Algorithm，CMAFA)，云算子惯性权重w生成方式可以详细描述为：

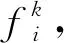
(3)

(4)

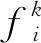
(5)

(6)

式中：k1、k2为控制系数。第k代惯性权重wk为[7]：

(7)

式中：惯性权重w的最小值wmin和最大值wmax。

CMAFA算法的萤火虫位置更新数学公式改进为：

xi(t+1)=wxi+β×(xj(t)-xi(t))+α×(rand-1/2)，

(8)

其中，主要引入惯性权重w改进基本FA算法的局部最优问题。

2 多目标的物流配送路径规划

2.1 问题描述

多目标的物流配送路径规划问题可以描述为[8-9]：对于配置了K辆农产品物流运输车的仓库而言，每个物流车的最大承载力为qk，其中(k=1，2，3，…，K)，对于整个配送环节的L个配送点位，每个配送点位需要装卸的农产品需求量要求gi(max(gi)≤

max(qi))，要求物流车辆在时间为Ti内完成该点位的农产品配送装卸需求，即每一个配送任务i必须在最早开始时间TEi和最迟开始时间TLi范围内完成。假设物流运输车比TEi点提前到配送点，则需要等待农产品。反之，配送装卸任务时间将增加。物流配送如图1所示，配送点空间位置如图2所示。

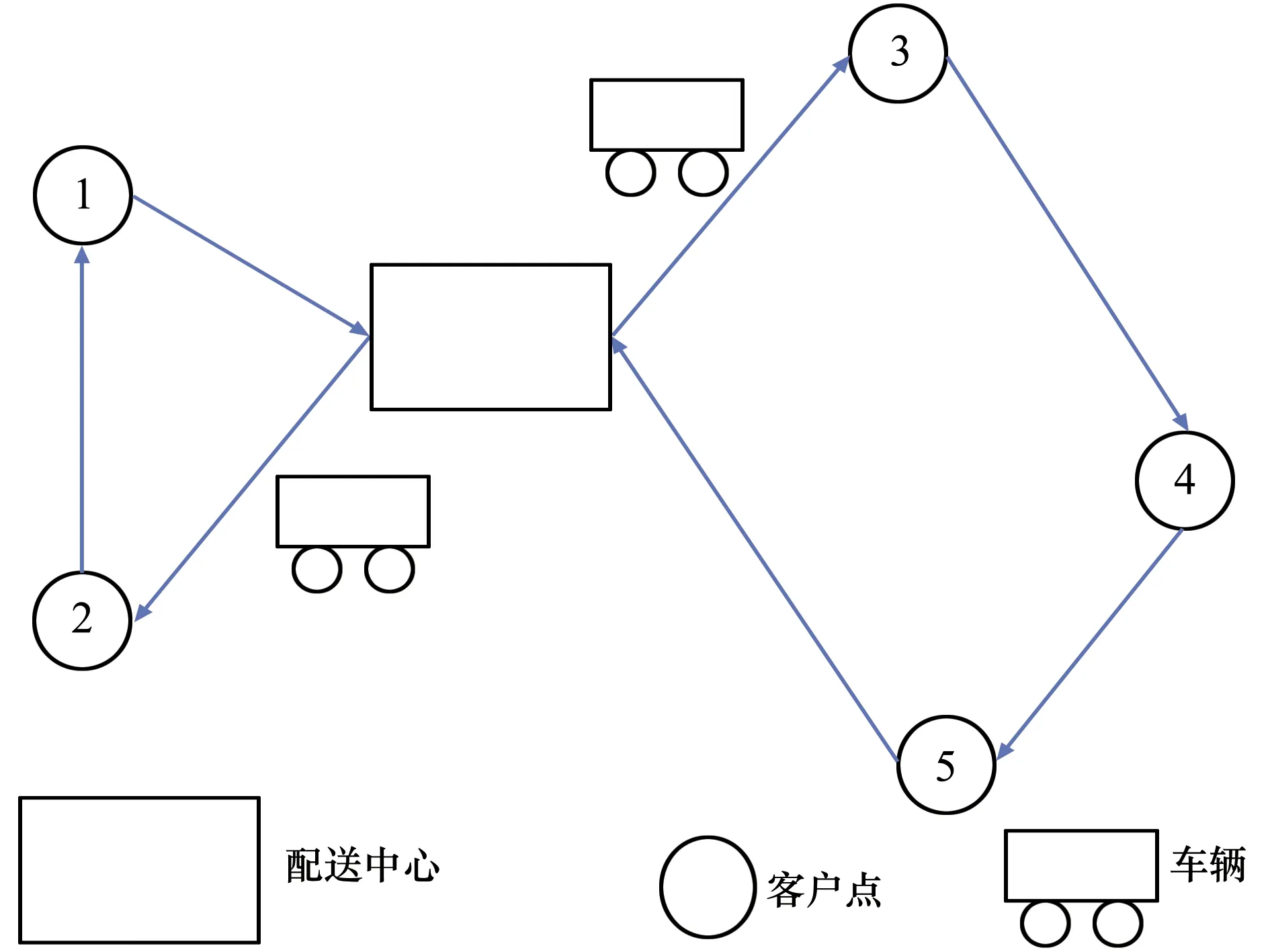
图1 配送示意图

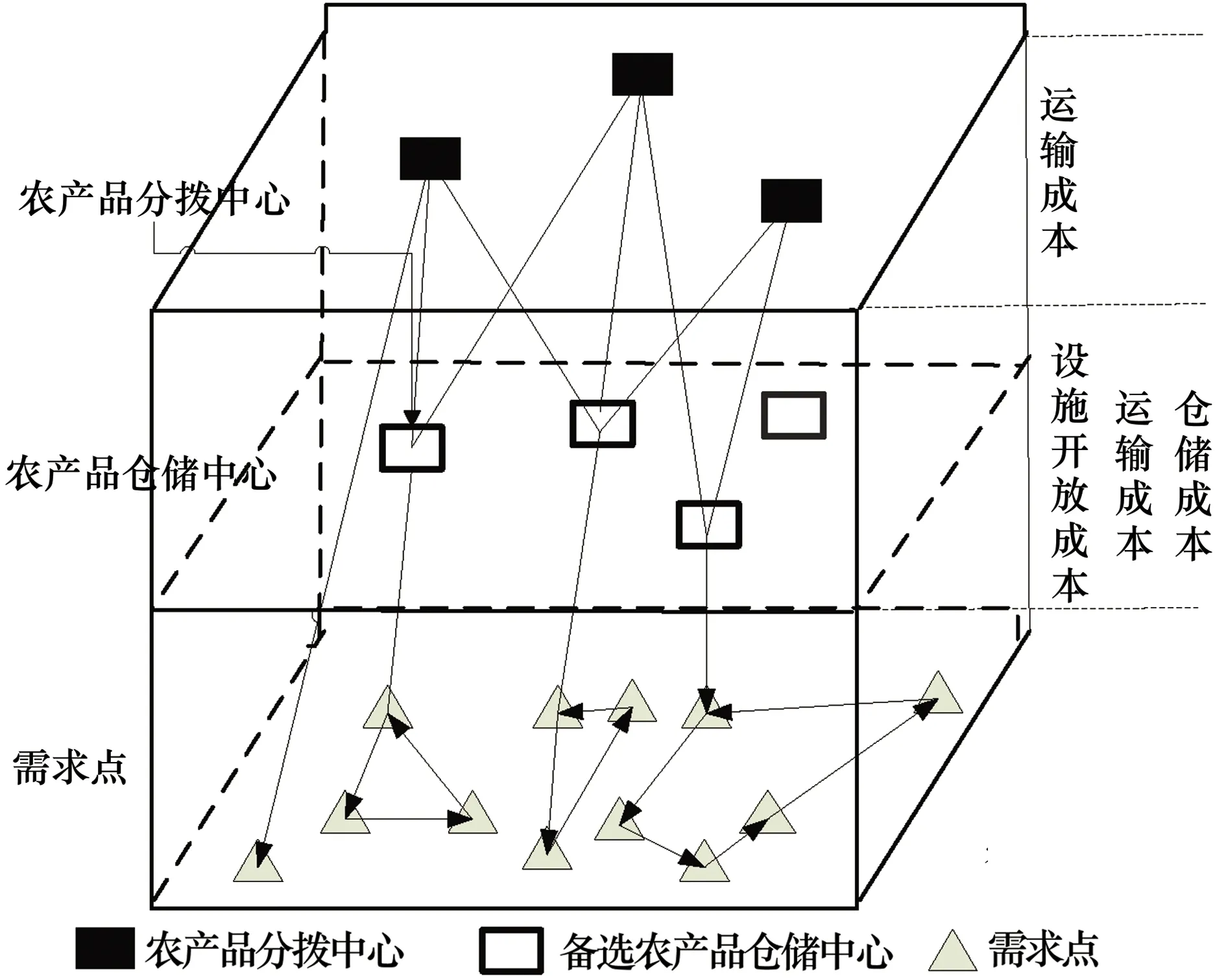
图2 配送点空间位置示意图

2.2 数学模型

定义0为农产品物流配货仓库，1，2，3，…，L为农产品对应的配送点位对应编号，设置i=(0，1，2，3，…，L)对应任务以及中心仓库变化，使用式(9)获得决策变量为[10]：

(9)

(10)

基于上述原理，生成农产品多目标物流车辆规划路径模型为：

(11)

(12)

(13)

(14)

式中：cij代表配送点i与配送点j之间运输花销；si代表物流配送车到配送点i所需时长；pE、pL分别代表农产品物流运输车出现提前、延后抵达配送点i过程中单位时间内所发生的成本。

本文模型汇总的全部配送点位均配套了物流车辆，而且对于每个点位与物流配送车站之间存在配送关系。

2.3 算法执行流程

萤火虫的表达方式的合理构建是实现本文规划模型的核心所在。算法执行过程中使用文献[11-12]设计了一个2L维空间对应L个配送点的农产品配送任务。当配送任务数为7，配送运输车为3时，配送任务编码为[1 2 3 4 5 6 7]。使用图3标识对应构造的萤火虫位置向量X，图3中萤火虫的位置可编码为农产品物流配送车辆和对应的配送路径。

图3 农产品配送车辆与路径编码示意图

编号为1、2、3的农产品配送车的规划路径分别为：1号车0、1、0；2号车0、4、5、3、2、0；3号车0、7、6、0。

基于改进萤火虫算法的多目标农产品物流配送路径规划流程如图4所示。

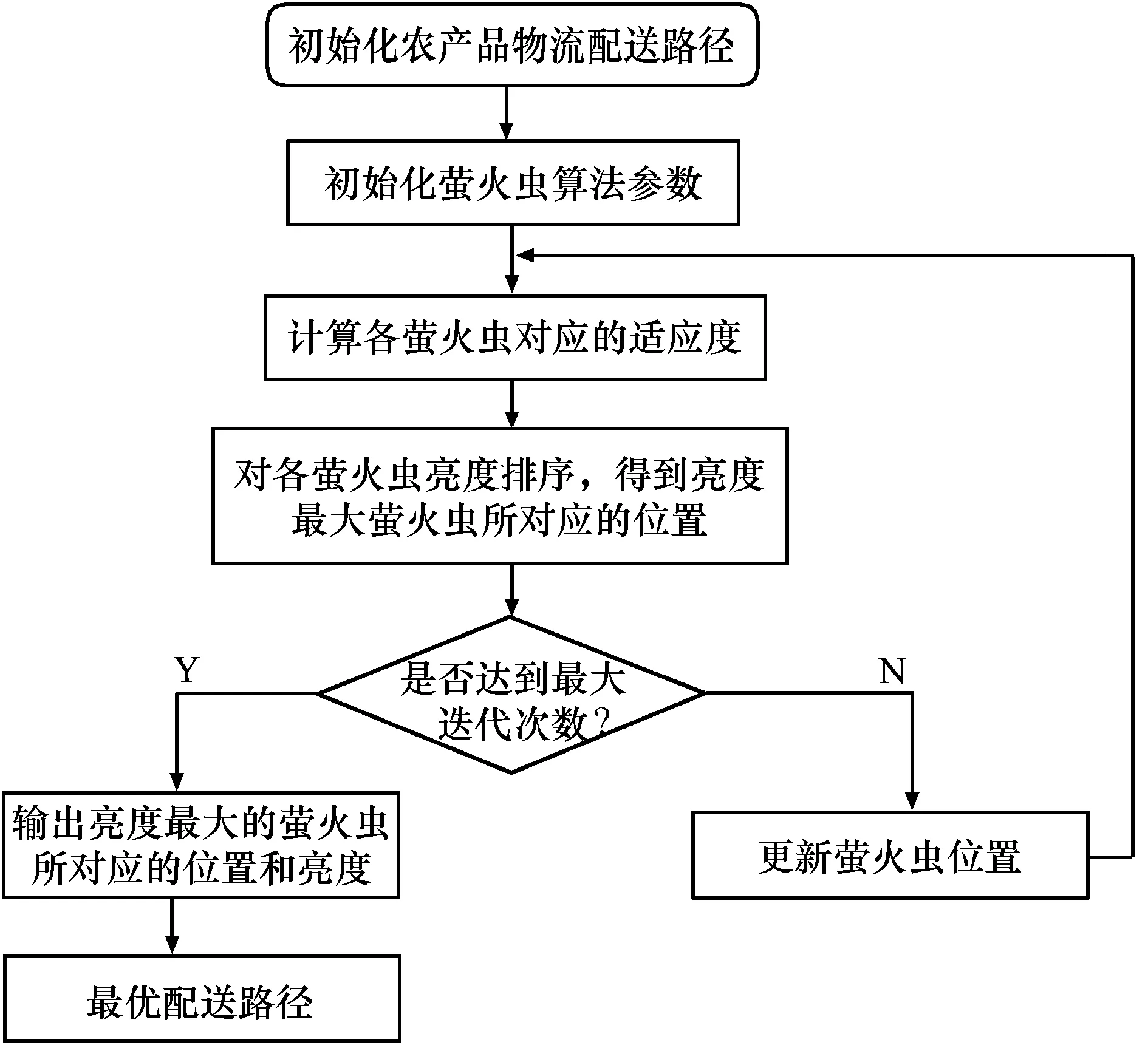
图4 农产品物流配送路径多目标规划流程

3 实验与结果分析

实验选择文献[13-14]作为实验对象，通过实验论证本文模型的路径优化的合理性和有效性，其中设置用户的配送点位以及中心仓库到各个配送点位距离矩阵如表1及表2所示。

表1 用户需求

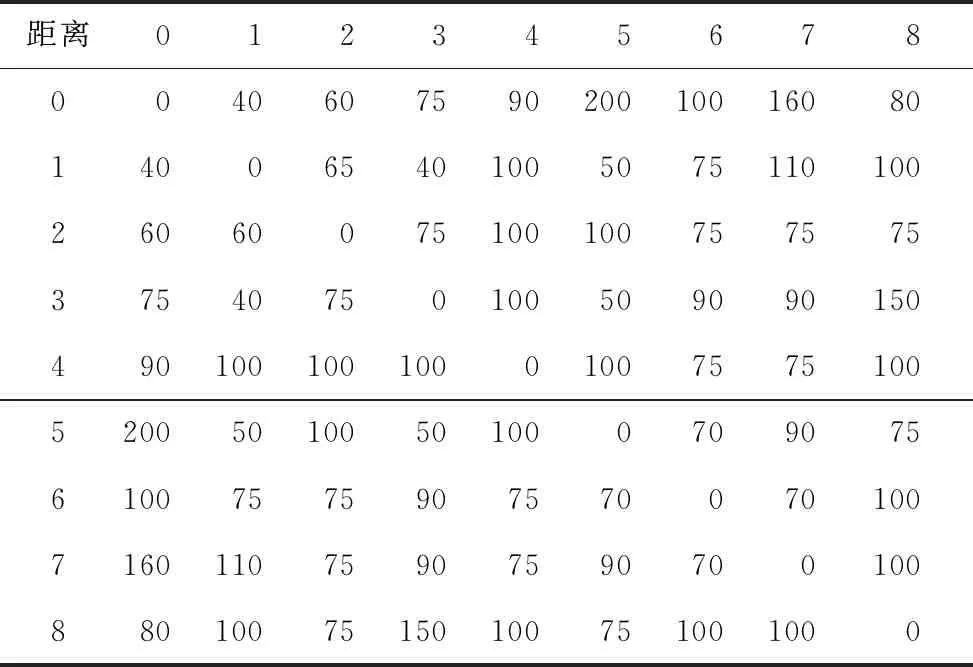
表2 距离矩阵

对比本文的CMAFA模型以及FA、GA，分别设置的算法参数为：1)CMAFA模型的初始参数：步长变换参数α取值为0.5、设置100次的最大迭代次数，对应的控制参数k1、k2取值为2。2)FA初始参数：步长变换参数α取值为0.5、设置100次的最大迭代次数。3)GA初始参数[15]：设置种群规模popsize为50，交叉概率Pc取值为0.7、变异概率Pm取值为0.1、设置100次的最大迭代次数，对比实验对应的结果如图6～图11所示。

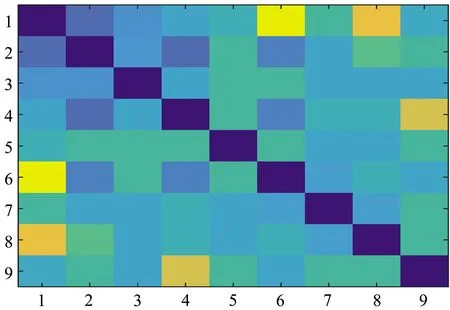
图5 距离矩阵图

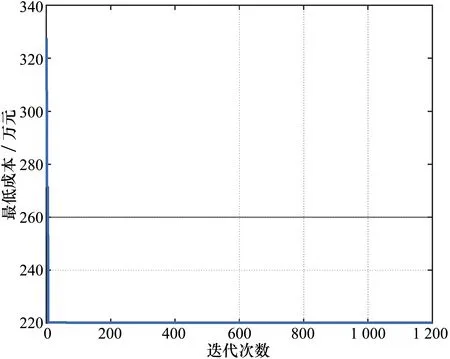
图7 CMAFA寻优收敛图

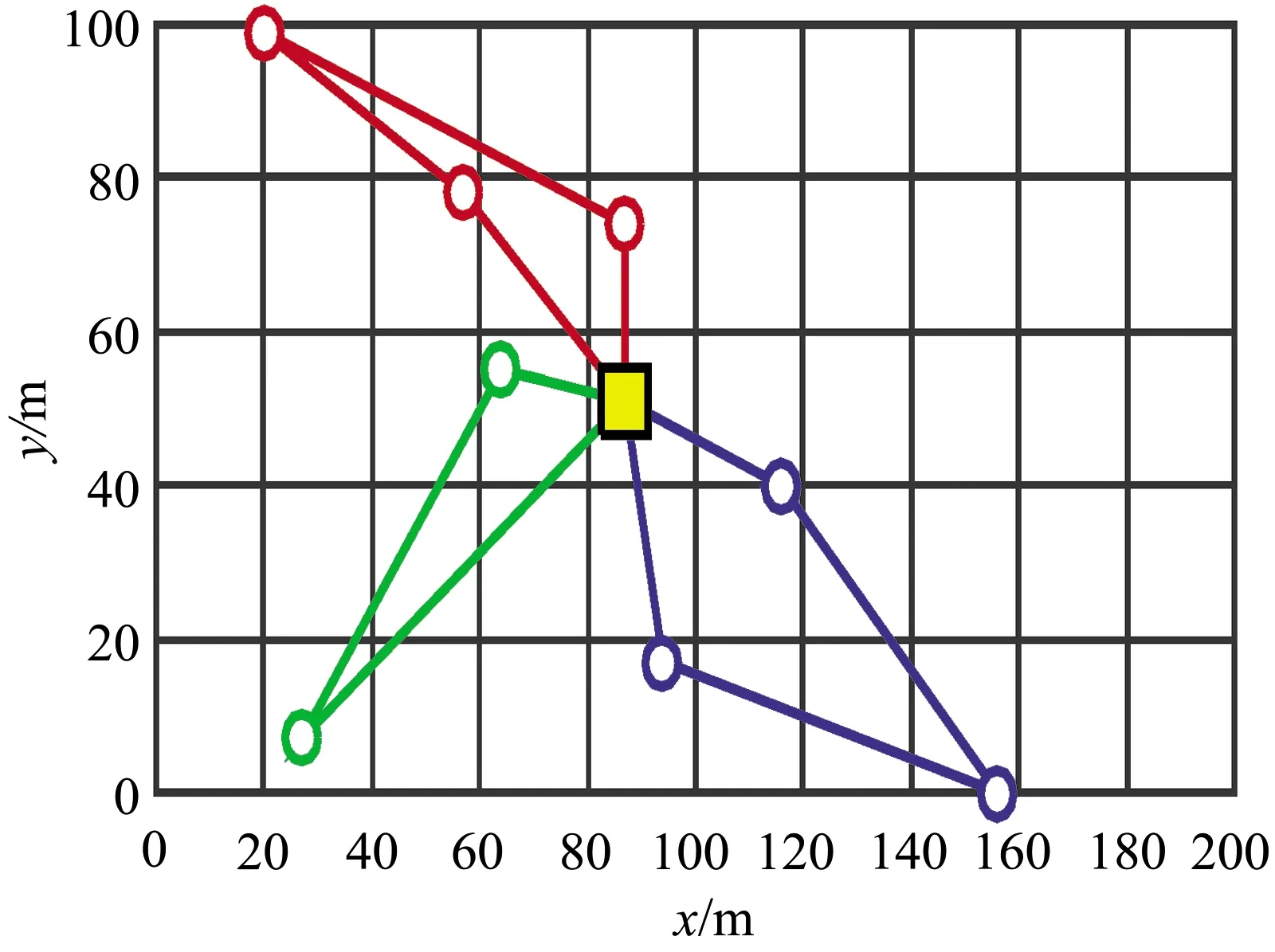
图8 FA配送路径

图9 FA寻优收敛图

图10 GA配送路径

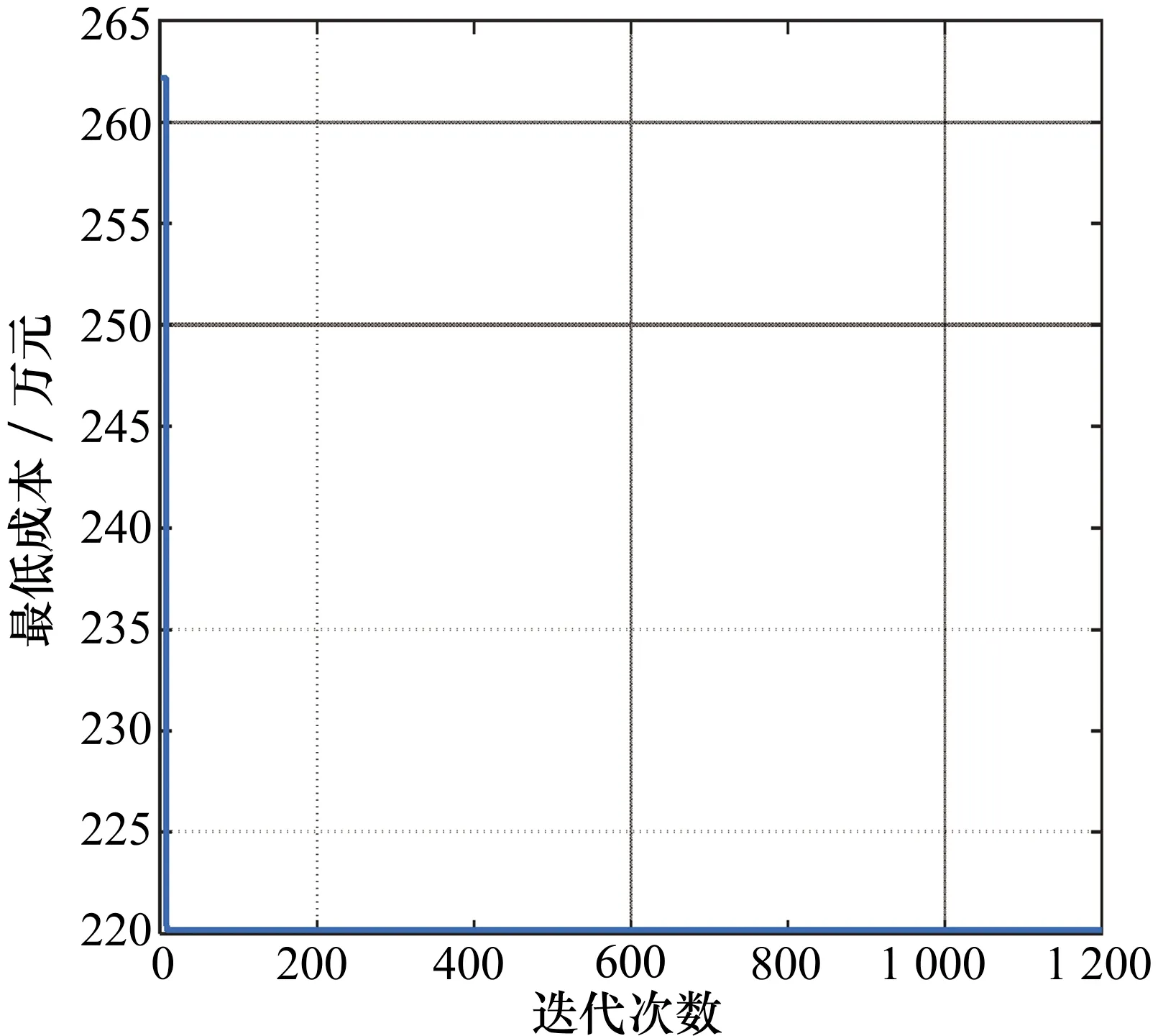
图11 GA寻优收敛图

由表3和图6～图11可知，与FA和GA相比，本文提出的CMAFA模型的搜索时间以及平均搜索耗能等方面，成本最小、效率最佳。另一方面，CMAFA模型的搜索成功率达到了67%，而FA与GA分别为46%和25%，进一步证明了本文提出的CMAFA模型对于农产品配送物流路径的规划方面具有较好的效果。

4 结论

本文对萤火虫算法进行了改进，建立了一种对农产品规划多目标物流配送路径的模型。针对传统萤火虫存在局部最优和收敛速度慢的缺点，提出一种自适应萤火虫算法。实验数据显示，对比经典的FA、GA等模型，本文提出的CMAFA模型的搜索时间以及平均搜索耗能等方面，成本最小、效率最佳。为农产品物流配送路径规划研究提供了新的思路和方法。