串级不稳定时滞过程的二自由度Smith预估控制
杜祎君,成 咪,任振涛
(太原科技大学 电子信息工程学院,太原 030024)
在化学、生物等相关工业领域中,常有不稳定过程的存在。与稳定过程相比,开环不稳定过程更难控制,而当过程中存在时滞时,由于系统稳定裕度的降低,进一步加深了控制器的设计难度,为此许多先进、高效的控制算法被不断地提出。文献[1-2]针对二阶不稳定时滞过程,基于内模控制与H2最优控制设计了PID控制器,显著提升了系统的抗扰能力。文献[3-6]使用Smith预估器补偿时滞,降低了不稳定时滞过程的控制难度,并通过二自由度控制策略,使系统同时获得了良好的设定值跟随特性与干扰抑制特性。文献[7-8]基于串级控制策略能快速抑制干扰的优势,提出了副回路采用内模控制,主回路采用设定值滤波器串联PID控制器的方法,该方法使系统的动态特性得到了很大提升。然而,串级控制存在的缺陷是如果主回路中存在较大的时滞,会导致系统闭环性能的降低。所以文献[9]在文献[7-8]的基础上,在主回路中采用了Smith预估器补偿时滞,进一步提升了系统的控制性能。而Smith预估控制的性能又依赖于过程模型的准确度。因此,为改善其控制性能,专家学者进行了大量的研究,如改进控制结构,优化控制器参数的整定、引入分数阶控制等。其中引入分数阶控制,不仅使系统控制更加灵活,而且能使系统获得更好的性能。在文献[10]提出了一种通过Bode理想传递函数设计的分数阶控制方法,该方法不仅结构简单而且参数整定方便。因此,将Smith预估控制与文献[10]提出的分数阶控制方法相结合,文献[11]实现了对稳定时滞过程的有效控制,不仅提高了系统的动态特性也提高了系统的鲁棒性。
目前,分数阶Smith预估控制大都针对稳定时滞过程设计。为此,本文提出了一种将分数阶Smith预估控制、二自由度控制、内模控制相结合的控制方法,实现了对串级不稳定时滞过程的有效控制。该方法在副回路中使用内模PID控制器,快速消除了进入副回路的干扰;在主回路中,首先使用PD控制器将不稳定时滞过程转换为稳定时滞过程,然后将分数阶Smith预估控制与二自由度控制相结合,实现了系统设定值跟随特性与干扰抑制特性的解耦,也通过分数阶控制的引入,提升了系统的鲁棒性。
1 不稳定时滞过程的串级二自由度Smith控制结构
不稳定时滞过程的串级二自由度Smith控制结构如图1所示。其中r1、r2、y1、y2、Gp1、Gp2分别为副、主回路的输入、输出与被控对象。Q1为副回路内模控制器。C2为稳定控制器,C3、C4分别为主回路的设定值跟随控制器与抗扰控制器。

图1 串级不稳定时滞过程的二自由度Smith预估控制结构
Gp1、Gp2为一阶加时滞模型。其传递函数为:
(1)
根据图1,副回路的闭环传递函数为:
(2)
(3)
当副回路模型精确,即P1m=Gp1:
(4)
(5)
主回路闭环传递函数为:
(6)
(7)
其中P2m0为P2m无时滞部分
(8)
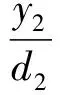
(9)
由式(8)、式(9)可知,主回路的设定值跟随特性仅与控制器C3有关,干扰抑制特性仅与控制器C4有关。因此,通过独立设计这两种控制器,可以分别处理主回路的跟踪与抗扰任务,避免了传统单自由度控制器须在设定值跟踪特性与干扰抑制特性之间折中选择的问题。
2 控制器设计
2.1 副回路控制器设计
副回路控制器采用内模控制方法设计:
(10)

其等效的反馈控制器C1为:
(11)

(12)
等效的反馈控制结构图如图2所示。
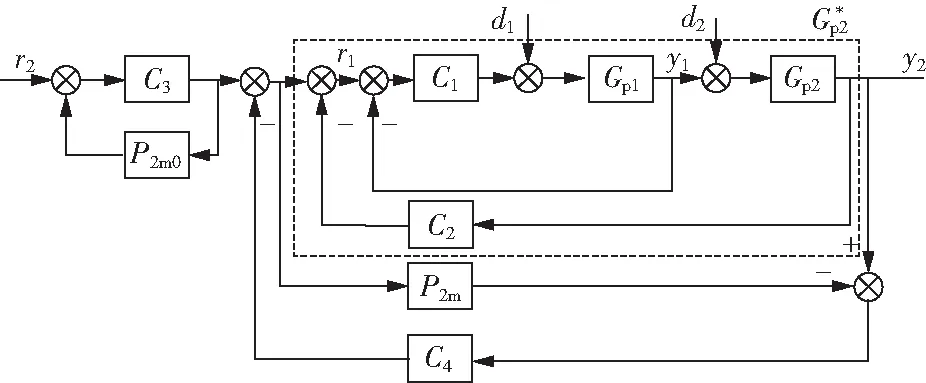
图2 等效的反馈控制结构图
2.2 稳定控制器设计

(13)
根据图1有:
(14)
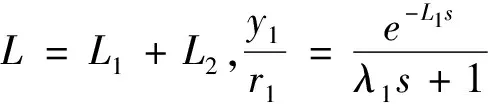

(15)

(16)

2.3 主回路设定值跟随控制器设计
主回路设定值跟随控制器C3采用了一种基于Bode理想传递函数设计的分数阶器与Smith预估器相结合的控制方法。其设计过程如下:
令主回路的开环传递函数为Bode理想传递函数加时滞形式:
(17)
其中:ωc为增益穿越频率,1≤α<2.

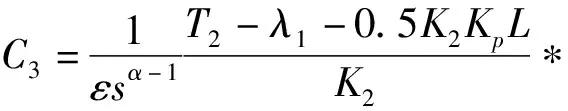

(18)
2.4 主回路抗扰控制器设计
为使系统具有抗扰性的同时又不失鲁棒性,抗扰控制器C4采用内模控制器设计的方法进行设计,其设计过程与副回路控制器设计方法相同,即
(19)
其中P2m0为P2m无时滞部分。
为提高系统的干扰抑制性能,滤波器f2选择为:
(20)
则抗扰控制器C4为:
(21)
3 控制器参数整定
3.1 副回路控制器参数整定
通过式(12)可知,副回路控制器C1需整定的参数为λ1.
根据2.2节有:
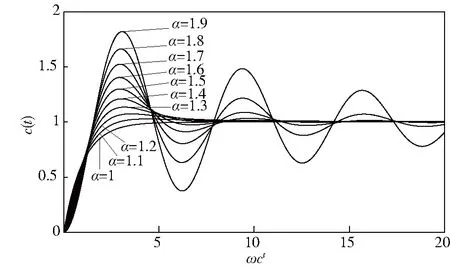
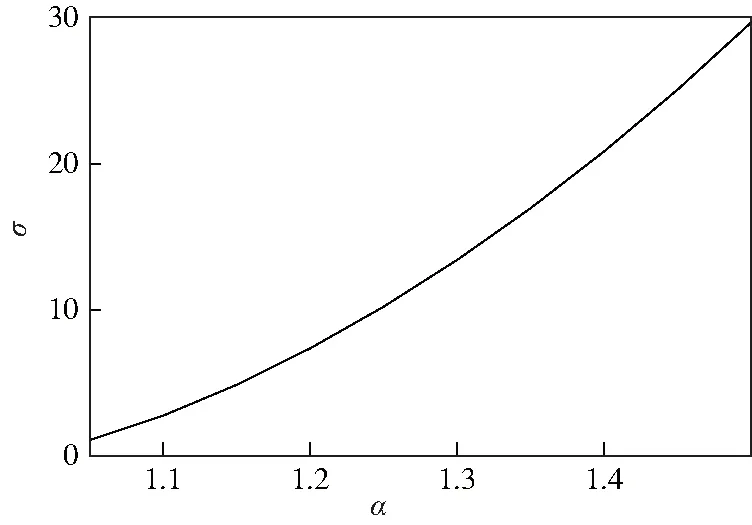
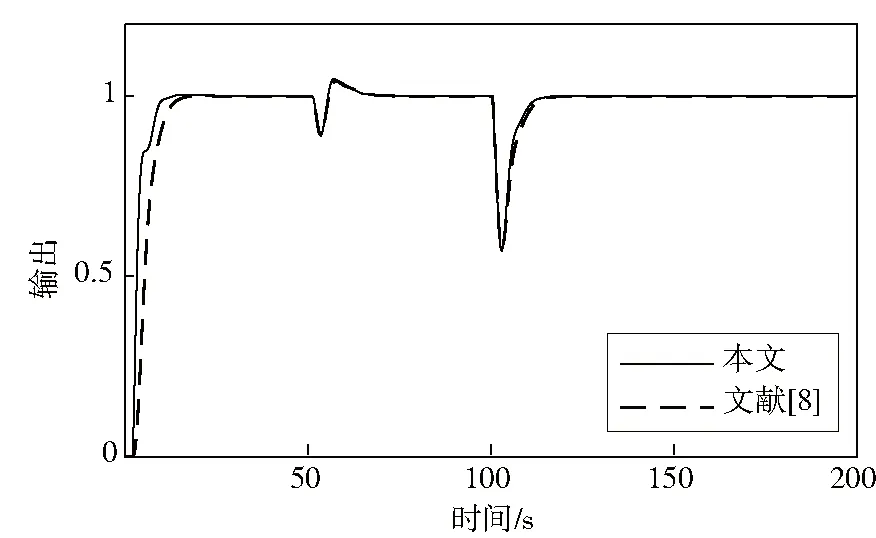
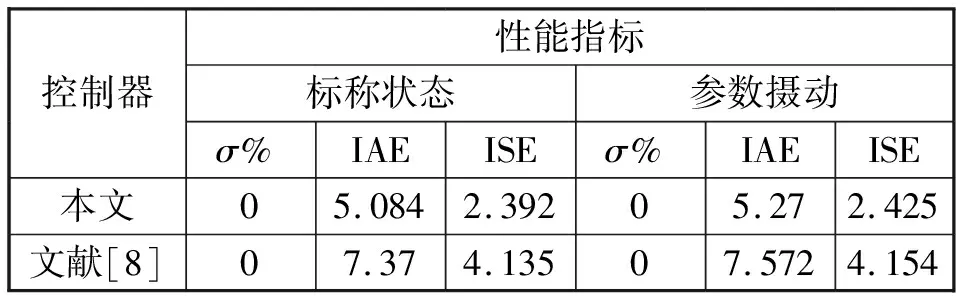
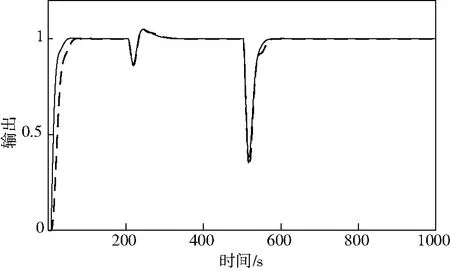
0<λ1 (22) 由文献[12-13]可知,增大λ1,系统的鲁棒性增强,减小λ1,系统的鲁棒性减弱。 根据式(13)可知,稳定控制器C2需整定的参数为Kp、Td. 根据2.2节有: (23) (24) (25) (26) 根据式(25)、式(26)有: (27) 从式(18)可以看出,主回路设定值跟随控制器C3需整定的参数为α、ε. 根据文献[10-11]可知,系统的超调量σ%受α的影响,系统的调节时间受α、ε的影响。根据Smith预估控制的特点,时滞项对系统的影响仅仅只是将输出信号延迟,并不影响系统的稳定性。因此可以先忽略时滞项,并通过单位阶跃响应来研究α、ωc对系统动态性能的影响。则其单位阶跃响应如下: (28) 其中:Eα为单参数的Mittag-Leffler函数。 通过式(28)可以看出,将ωct作为一个整体,在[1,2]之间改变的α的值,即可得到系统的单位阶跃响应。其单位阶跃响应图如图3所示。 图3 不同α值的单位阶跃响应图 通过图3可以看出,α增加,系统的超调量也增加。而过大的超调也会导致系统的稳定性变差。因此,选择超调量σ%<30%,即近似选择1≤α≤1.5来设计控制系统。根据图3,可以得出当α∈[1,1.5]时与σ,调节时间ts(2%误差)之间的关系。α与σ关系图为图4,α与ts关系图为图5. 图4 α与σ关系图 图5 α与ts关系图 通过曲线拟合技术,可以得到α与σ之间关系式为: (29) α与ts之间的关系式为: (30) 根据系统所需的时域指标,据式(29)、(30)可计算出α、ωc.而从式(17)有ε=(1/ωc)α,则可通过ωc,计算出ε. 由式(21)可知,主回路抗扰控制器需整定的参数为λ2、β1、β2. 经大量仿真实验分析,当λ2∈[0.8L,1.2L],可以使系统获得良好的抗扰性能。 (31) β2、β1满足以下约束: (32) (33) 则有: (34) [1/p2-1/p1] (35) 在实际条件下,常有参数摄动的情况发生。因此,在设计控制器时须考虑参数摄动的问题。闭环系统的这种鲁棒稳定性可以用小增益定理来确定。根据该定理,闭环系统鲁棒稳定的充要条件为: (36) T(jω)为补灵敏度函数,δm(jω)为过程乘性不确定性界。 (37) Gp为实际过程的传递函数,Gm为设计控制器所使用的过程传递函数。 如果同时存在不确定性时间常数,不确定性时滞与不确定性过程增益,则控制器参数应该满足: ‖T(jω)‖∞< ∀ω≥0 (38) 在本文中补灵敏度函数T(s)为: (39) 则将式(39)代入式(38)中得: ∀ω≥0 (40) 从式(40)可知,通过调整λ2的值,可以控制系统鲁棒稳定性。因此,λ2须选择合适的值,使系统在不失鲁棒稳定性的前提下,又能使系统具有良好的干扰抑制特性。 为验证本文提出的控制方法的有效性,以超调量σ%、IAE、ISE为性能指标,对串级不稳定时滞过程进行了仿真研究,并与文献[8]中的控制方法进行了比较。为保证比较的公平性,调整控制器参数,使两种控制系统的超调量相同,并比较IAE、ISE的值,其值越低说明控制性能越好。 例1参考文献[8]中的实例1: 副回路参数选择与文献[8]同样的参数,λ1=0.3.选择Kp=2,Td=0.5L=0.4695.根据计算,文献[8]中超调σ%=0,则令σ%=0,根据式(29)计算出本文中的α=1.0145,选择ε=1.774 6,λ2=1. 令r2为单位阶跃信号,在50 s,100 s时,分别在d1、d2处加负单位阶跃干扰,得到的响应曲线如图6所示。K1、K2、T1、T2、L1、L2参数同时增加10%,得到的响应曲线如图7所示。性能指标如表1所示。 图6 例1干扰抑制响应曲线 图7 例1 参数摄动10%时,系统响应曲线 表1 例1控制系统性能指标 从图6-图7以及表1中可以看出,与文献[8]相比,本文所提出的方法拥有更好的闭环性能与鲁棒性。 例2参考文献[8]中的实例2: 副回路参数选择与文献[8]同样的参数,λ1=1.选择Kp=2,Td=0.5L=3.根据计算,文献[8]中超调σ%=0,则令σ%=0,根据式(29)计算出本文的α=1.014 5,选择ε=8.690 1,λ2=5. 令r2为单位阶跃信号,在200 s,500 s时,分别在d1、d2处加负单位阶跃干扰,得到响应曲线如图8所示。K1、K2、T1、T2、L1、L2参数同时增加10%,得到的响应曲线如图9所示。性能指标如表2所示。 图8 例2干扰抑制响应曲线 图9 例2参数摄动10%时,系统响应曲线 表2 例2控制系统性能指标 从图8-图9以及表2可以看出,本文所提出的方法在标称情况下与参数摄动10%的情况下均具有良好的控制效果,且优于文献[8]方法的控制效果。 本文基于一种二自由度Smith预估控制方法,实现了对串级不稳定时滞过程的有控制。该方法不仅通过内模PID控制器快速消除进入副回路的干扰,而且在主回路中使用分数阶Smith预估控制与二自由度控制相结合的控制策略,提升了系统的闭环性能。经仿真实验验证,该方法不仅参数整定简单,而且提高了系统的动态特性、稳态特性与鲁棒性。3.2 稳定控制器参数整定

3.3 主回路设定值跟随控制器参数整定

3.4 主回路抗扰控制器参数整定

4 鲁棒性分析
5 仿真分析



6 结论

