基于改进多目标粒子群算法的平原坡水区水资源优化调度

王文君，方国华，李 媛，闻 昕，郭玉雪

(1.河海大学水利水电学院，江苏 南京 210098； 2.南京水利科学研究院水工水力学研究所，江苏 南京 210029)

平原坡水区大都是粮棉油的主要生产基地[1]，但平原坡水区河道坡度十分平缓[2]，河流密布，流动性复杂，再加上自然条件和其他因素的影响，致使流域内拦蓄能力不足，没有大型蓄水工程，水源无保证，区域水系难以形成联合调配体系、区域内水资源供需关系紧张、缺水问题突出，严重影响了沿线经济发展。另一方面，平原坡水区有大量的泵、闸、渠等水利工程，能够担负起水资源调配的综合性任务[3]。如何充分发挥水工建筑物效能、河道蓄水能力，改善灌排工程体系，统筹利用天然径流和外调水进行优化调度，结合受水区需水情况对水量进行优化分配，实现区域多水源的互济互调，在降低受水区缺水率的同时，充分发挥生态效益和经济效益是亟待解决的问题[4]。

水资源优化调度往往涉及多个目标[5]，常用的线性规划、动态规划、大系统分解协调等解法在处理多目标复杂系统时的求解效率难以满足实际需求。近年来发展起来的模拟生物演变过程的智能优化算法逐渐成为求解水资源优化调度模型的主要手段，主要有遗传算法(GA)[6-8]、粒子群(PSO)算法[9]、蚁群算法(AG)[10]等。NSGA-Ⅱ算法是遗传算法中最具代表性的方法[11]。该算法基于1993年Srinivas和Deb提出的NSGA算法，改进了解集的构造，提高了求解效率，并保证了解集的有效性和优越性[12-13]。粒子群算法则具有结构简单、易于实现、搜索速度快等优点[14]，很多学者将其运用于水资源调度并取得了一定的效果。闫堃等[15]利用多目标粒子群(multi-objective particle swarm optimization， MOPSO)算法求解滨海地区平原河网、平原水库群和远距离调水工程体系的水资源多目标优化调度模型。王万良等[16]采用多目标混合粒子群算法求解梯级小水电群动态多目标优化调度模型。翁士创等[14]将粒子群算法应用于旱情紧急情况下的韩江流域水资源调度模型，取得了较好的综合效益。

针对PSO算法存在容易陷入局部极值点、早熟等缺点，本文从惯性因子及学习因子选择、外部档案维护以及全局最优选取策略3个方面进行改进，对比传统的NSGA-Ⅱ算法，测试改进MOPSO算法在部分ZDT函数上的表现，验证算法的可行性及优越性，最后以宿迁市黄河故道及以南地区水资源优化调度为例，采用改进MOPSO算法求解平原坡水区水资源优化调度模型。

1 平原坡水区水资源优化调度数学模型

为实现期望效益，提高泵闸运行经济效益，模型选取受水区缺水量和泵站提水量两个优化目标，将生态目标转化为约束条件进行处理[17]。根据平原坡水区系统构成和特点考虑河道水量平衡约束、泵站工作能力约束、闸站下泄流量约束、河道调蓄能力约束、河道水位要求约束、生态约束和非负约束，构建平原坡水区水资源优化调度模型。

1.1 目标函数

1.1.1经济目标

在充分利用现有水资源的前提下，区域用水不足的部分由区域内泵站提水补充，总提水量越小，则越能有效控制提水成本，因此经济目标取总提水量最小为目标，目标函数为

(1)

式中：t为时段序号；T为时段数；a为泵站编号；m为泵站数量；Pa,t为t时段泵站a的提水量。

1.1.2社会目标

社会目标可以通过总缺水量大小来衡量，因为区域用户缺水量关系社会发展和人民的生活水平，进而影响社会效益。其目标函数为

(2)

式中：b为分区编号；n为分区数量；Db,t为t时段b分区的缺水量。

1.2 约束条件

a.河道水量平衡约束。针对有调蓄能力的河道，应满足的水量平衡方程为

Vi,t+1=Vi,t+WPi,t+Wi,t+WXi-1,t-WRi,t-WXi,t

(3)

式中：Vi,t为t时段河道i的蓄水量；WPi,t为t时段抽过境水入河道i的泵站提水量；Wi,t为t时段流入河道i的天然径流和地下水资源量；WRi,t为t时段河道i的供水量；WXi,t为t时段河道i的下泄水量。

b.泵站工作能力约束：

0≤Pa,t≤Pa,t,max

(4)

式中Pa,t,max为t时段泵站a的最大工作能力。

c.闸站下泄流量约束：

0≤Xl,t≤Xl,t,max

(5)

式中：l为闸站编号；Xl,t、Xl,t,max分别为t时段闸站l的下泄流量和最大下泄流量。

d.河道调蓄能力约束：

Vi,t,min≤Vi,t≤Vi,t,max

(6)

式中Vi,t,min、Vi,t,max分别为t时段河道i的最小和最大蓄水能力。

e.河道水位要求约束：

Zi,t,min≤Zi,t≤Zi,t,max

(7)

式中Zi,t、Zi,t,min、Zi,t,max分别为t时段河道i的水位、最低水位和最高水位。

f.生态约束：

Qi,t≥QEi,t,min

(8)

式中Qi,t、QEi,t,min分别为t时段河道i的流量和所要求的最小生态环境流量。

g.非负约束。所有参数满足非负约束条件。

2 改进MOPSO算法

2.1 PSO算法

PSO算法是基于鸟群觅食行为发展起来的一种以群体协作及信息共享为基础的智能搜索算法[18]。在该算法中每个粒子的速度和位置按照如下方程来更新：

(9)

(10)

式中：k为迭代步数；vs,d为粒子s在d维空间上的速度，vs,d∈[vmin,vmax]；w为惯性因子；c1、c2为学习因子，通常取c1=c2=2；r1、r2为[0,1]范围内的均匀随机数；ps,d为粒子s在d维空间上的个体极值点；pg,d为d维空间上的全局极值点；xs,d为粒子s在d维空间上的位置。

2.2 惯性因子和学习因子的选取

日灼病是因为阳光太强、温度过高导致植株叶肉细胞灼伤失去活性，从而减弱苗木整体生长势的一种生理病害[3-4]。由表4可知，圃地内设置的对照组大棚没有覆盖，通过一个夏秋季，苗木日灼现象严重。可见，低海拔地区香榧育苗和栽培时没有遮荫措施是不行的，遮荫措施可以有效把直射光转成散射光或漫射光线，极大减轻了苗木日灼病发生。

(11)

式中：wmax、wmin、wmid分别为惯性因子最大值、最小值和中间值，本文分别为3.0、-1.0和1.0；fj,s为粒子s的适应度值；h为目标函数的总个数。该策略保证种群中的每个粒子都能朝正确的方向飞行，更快地趋近Pareto前沿。

本文采用的粒子群算法依据迭代步数调整学习因子，具体策略为

(12)

式中：k为当前迭代步数；kmax为最大迭代次数。c1随迭代步数的增加递减，而c2则与之相反。该策略使粒子在飞行前期更注重本身的历史轨迹，而飞行后期则更注重种群的位置信息。本文cmax和cmin的取值分别为2.0和0.5。

2.3 全局最优选取策略

由于缺乏标准方法判断多目标优化问题中非劣解集的优劣，本文采用基于距离的方法选取全局最优pg,d，即全局极值点。假设A和B是外部档案中的2个非劣解，则A和B在目标空间的距离定义为

(13)

对于档案中的非劣解A，采用改进的MOPSO算法寻找与A最近的2个解C和D，并得出A的特征距离：

(14)

比较所有非劣解的特征距离并寻找特征距离最大的解作为全局最优。如果几个解的特征距离相同则从中随机选取全局最优。该策略能够避免粒子群陷入局部最优，从而更加接近Pareto前沿。

2.4 外部档案的初始化和维护策略

改进MOPSO算法依据解的支配关系和距离关系来实现外部档案的维护。解之间的支配关系定义为：对于A和B两个解，若A的全部目标函数均不大于B的目标函数，且至少有一个目标函数小于B，那么A解支配B解；反之则B解支配A解。若以上两个条件均不满足，则两者互不支配。

程序开始时将粒子逐个放入外部档案，依次比较粒子与档案中已有的解。若粒子支配档案中的某个解，则删除档案中的该解。假如档案中不存在支配该粒子的解，则把这个粒子放入档案。

同样，每次更新粒子的速度和位置取得新解之后，依照上述规则将其与档案中已存在的非劣解进行比较，在不被档案中任一解支配时在档案中放入该解。如果档案中成员的数量超过程序设定值，则比较档案中所有解之间的拥挤程度，并随机删去距离最近的两个解中的一个，而后重新计算解成员之间的距离。

2.5 算法基本流程

改进MOPSO算法的基本流程如图1所示。

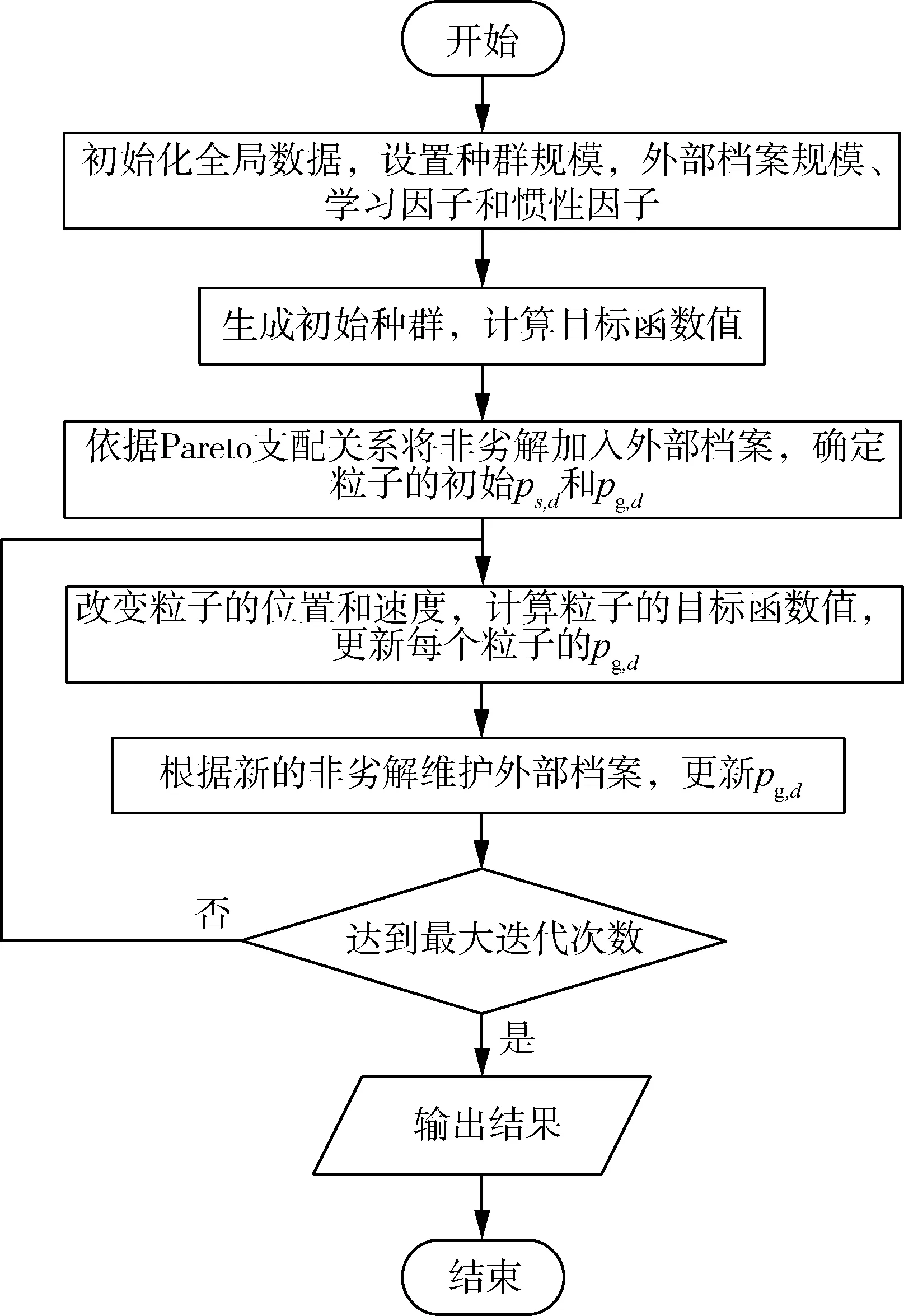
图1 改进MOPSO算法基本流程图

2.6 算法测试

采用ZDT测试函数对改进MOPSO算法进行了测试，选取的ZDT测试函数包括ZDT1、ZDT2、ZDT3和ZDT6[19]。改进MOPSO算法参数的设置为：种群规模为100，外部档案规模为100，最大迭代次数为5 000，惯性因子和学习因子的选取如前文所示。测试结果与传统的NSGA-Ⅱ算法求解结果以及真实的Pareto曲线的对比如图2所示。NSGA-Ⅱ算法采用同样的种群规模、外部档案规模、最大迭代次数。

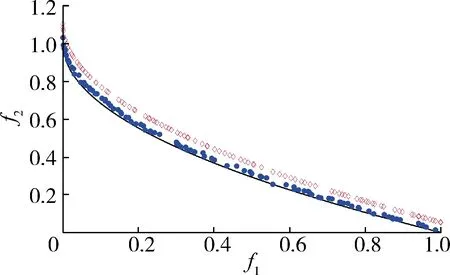
(a) ZDT1

由图2可知，改进MOPSO算法对测试函数的优化结果均与真实非劣前沿保持一致，所得到的解优于NSGA-Ⅱ算法求解得到的解；从分布性来看，改进MOPSO算法也表现优异，优化结果分布均匀。综上可见，无论是收敛度还是分布性，改进MOPSO算法在处理多目标问题中均有明显优势。

3 实例研究

受黄河冲积影响，宿迁市形成了大面积平原坡水区，地势上以黄河故道为分水岭，向南北两侧逐渐倾斜。本文研究范围位于宿迁市黄河故道以南、南淮泗河以西、市界以东、宿城与泗洪县界以北，由宿迁市黄河故道流域和黄河故道以南地区组成，涉及宿城区、泗阳县两个行政区，总面积1 674.2 km2。

宿迁市黄河故道及以南地区水资源调度系统通过七堡枢纽、运南北渠首等泵站将骆马湖及中运河的水提到黄河故道，并经由皂河地涵、蔡支闸等11级闸站向下游输水，同时沿途向运南灌区、船行灌区、皂河灌区和区域内其他用水户供水，水流最后流入洪泽湖；其中运南灌区还可从洪泽湖提水补充。系统概化图如图3所示。

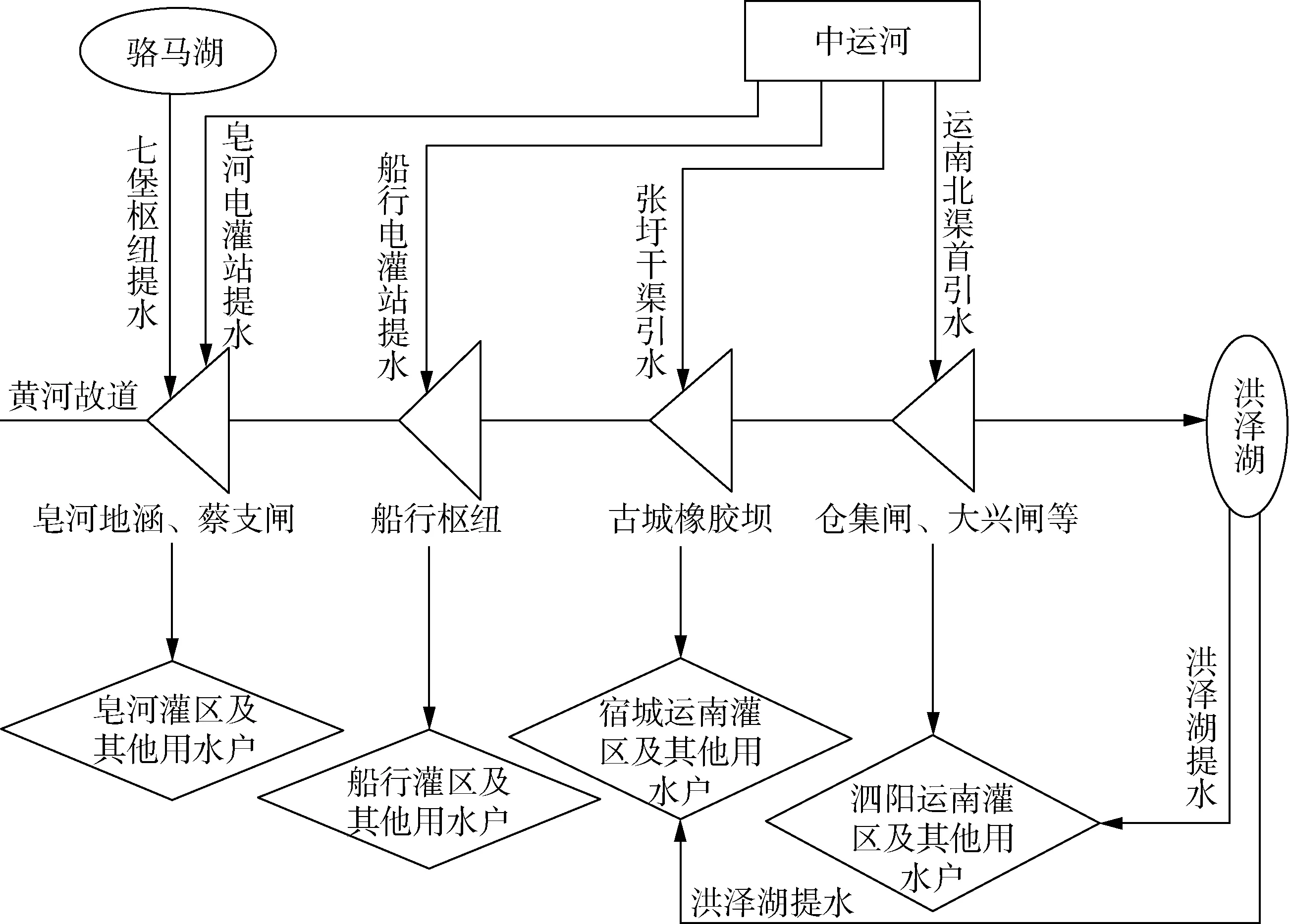
图3 宿迁市黄河故道及以南地区水资源系统概化图

宿迁市黄河故道及以南地区水资源优化调度模型包括多水源、多用户，模型的目标函数和约束条件如前文所述，来水量、需水量、泵站、闸站等的详细信息限于篇幅不具体列出，最小生态环境流量取河道外生态环境需水量，即保护、修复或建设生态环境需要通过人工供水设施补充的水量，包括城镇生态环境需水、林草植被建设和湿地保护修复等用水。模型基于2013年(现状水平年)水资源供需平衡情况，以月为计算时段，以水文年为计算周期，以各区间需水和来水情况为模型输入，利用改进MOPSO算法对模型进行求解。在50%、75%、95%设计频率来水条件下用改进MOPSO算法求解调度模型，所得的Pareto前沿如图4所示。

由图4可以看出，受水区缺水量与泵站提水量之间呈明显的负相关关系。若减少泵站提水量，则受水区缺水量增大；反之，若要减少受水区缺水量，则必将以牺牲经济效益为代价；社会效益与经济效益之间表现出对立性。对比3种不同频率来水调度方案可见，当来水量较大时，需要的泵站提水量较小，且受水区缺水量也较小，即两者之间对立性较弱。总的来说，各频率来水调度方案集在空间中分布均匀，两个目标函数值分布范围较广，该Pareto前沿可为决策者提供较为全面的决策信息，表明改进MOPSO算法作为一种新的多目标优化问题求解方法，具有较好的可操作性，可有效运用于具体的工程实践中。

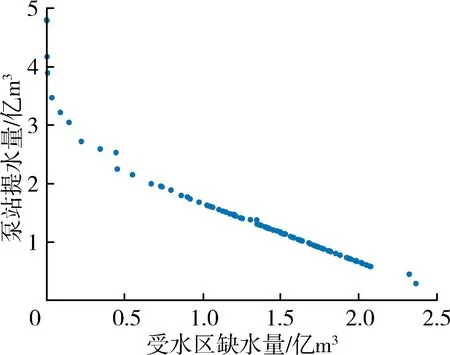
(a) 50%

选取几种典型调度方案如表1所示，各典型调度方案侧重于不同的调度目标。以50%设计频率为例，方案1为受水区缺水量最小对应的方案，明显侧重于社会效益，这样不可避免的导致泵站提水量增加，从而影响经济效益；而方案3则侧重于经济效益，减小泵站提水量从而降低提水成本，但其缺水率接近50%，忽视了区域用户的用水需求，违背了社会目标；方案2为最佳均衡解，其缺水率为10%左右，但提水量仅为方案1的一半，因此可以看作是方案1和方案3的折中。可见切合实际的调度方案需要权衡社会效益和经济效益，在实际应用中，决策者可根据实际需要进行多属性决策从而选定适当的调度方案。

表1 50%、75%、95%设计频率下典型调度方案集

4 结 语

本文针对平原坡水区水资源优化调度的特点建立了相应的数学模型。根据粒子群算法基本理论，从惯性因子及学习因子选择、外部档案维护和全局最优选取策略3个方面进行改进，并对比改进算法与传统的NSGA-Ⅱ算法在求解测试函数中的表现，验证了改进MOPSO算法在处理多目标问题上的良好性能。对宿迁市黄河故道及以南地区水资源优化调度进行了实例研究，采用改进MOPSO算法求解模型得到Pareto前沿。结果显示，两个目标函数值分布范围较广，且各频率来水调度方案集在空间中分布均匀，表明改进MOPSO算法是一种解决多目标约束和复杂非线性系统问题的有效优化方法。