Spiking-free HGO-based DSC for flexible joint manipulator

Dezhi KONG, Wendong WANG,*, Yng WANG, Juno ZHANG,Yiki SHI, Lingyun KONG

a School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China

b Shaanxi Engineering Research Center of Controllable Neutron Source, School of Science, Xijing University, Xi’an 710123, China

KEYWORDS Dynamic surface control;Flexible joint manipulator;High-gain observer;Mismatched uncertainties;Partial states feedback;Spike suppression

Abstract The tracking control problem for Flexible Joint Manipulator Control System (FJMCS)with unmeasurable states is addressed in this paper. Firstly, a High-Gain Observer (HGO) is constructed to estimate the unmeasurable states and the uncertainties. Then, a Dynamic Surface Control(DSC)scheme is developed by using the estimation of HGO.The newly proposed controller has two advantages over the existing methods: (A) a novel Spike Suppression Function (SSF) is developed to avoid the estimation spike problem in the existing HGO-based controllers. (B) Unlike the existing observer-based partial feedback control scheme that can only estimate the unmeasurable states, the proposed HGO can estimate both the unmeasurable states and uncertainties. The closed-loop system stability is proved by the Lyapunov theory. Simulation results demonstrate the effectiveness of the proposed controller.

1. Introduction

With the development of mechanical,control and sensor technology, the design of robot has made great progress and is gradually replacing human in the fields of repetitive labor,emergency rescue, home service, etc.In robot system, the robot manipulator has a very important role as the endeffector of the robot which interacts with the external environment. For the robot manipulator, many studies on control strategies for different kinds of robot manipulator components have been completed. And, among these strategies, the disturbance attenuation control takes an important role since the robot manipulator system is a typical nonlinear uncertain system, and the uncertainties can be caused by the unmodeled dynamics, external environment and parameter uncertainties.

Compared with the conventional Rigid Robot Manipulator(RRM), the Flexible Joint Manipulator (FJM) has become a research hotspot increasingly since it has several advantages,such as smaller actuator, light weight, lower cost and better maneuverability. However, the flexibility of FJM brings more complex uncertain characteristics of dynamic model.The dynamic model of conventional RRM is a low-order(twoorder) matched uncertain system. But the dynamic model of FJM is a typical high-order(four-order)mismatched uncertain system.

To solve the mismatched uncertain problem, the Backstepping Control Method (BCM)is a good candidate. The main advantage of BCM is that it can suppress the mismatched uncertainties through a step-by-step recursive process. Some BCM-based methods for FJM have been developed, such as BCM-based adaptive control, BCM-based fault-tolerant control, BCM-based neural network control, BCM-based intelligent controland BCM-based L2-gain control. For conventional BCM, the computation needed for backstepping is very tedious and complicated, and this is so called the problem of‘‘differential explosion”.To solve this problem,the Dynamic Surface Method (DSM) was proposed. The DSM can not only suppress the mismatched uncertainties by the step-by-step recursive process like BCM, but also adopt a low-pass filter to avoid the explosiveness of backstepping.Then an adaptive fault-tolerant control for FJM based on DSM was proposed,and the complex differential calculation for backstepping in Refs. 18–22 can be avoid by the low-pass filter.However,in order to complete the step-by-step recursive process, the BCM-based and DSM-based controllers in Refs.19–22 not only need to measure the states of link,but also need the states of motor for feedback. Thus, the measurement systems for the controllers in Refs.18–22 are much more complex than the measurement system for the conventional RRM controller which only needs the states of link.

As a control method which only needs the measurements of partial states,the Output Feedback Control(OFC)scheme can simplify the measurement system for high-order systems,significantly. Some control schemes for FJM based on OFC have been developed to simplify the measurement system. A control scheme which only requires the feedback of position states was developed for FJM, in which an observer was designed to estimate the unmeasurable link and the actuator velocity, but the uncertainties of FJM were not considered in Ref. 31. The unmeasurable velocities of link and motor were estimated by an approximate differential observer,and a complex adaptive control law was proposed to eliminate the effect of the uncertainties. A high-gain observer was designed to generate pseudo signals for unmeasurable states,and an adaptive law of the projection type was developed to estimate the unknown feed-forward term.

To guarantee the observation and control precision, the observer gains of the observers in Refs. 31–33 should be chosen as the high gains. Thus, the observers used in Refs. 31–33 are typical High-Gain Observer (HGO). However, the undesirable spike problem can be caused by the high observer gains when the initial values of estimate and true states are not equal. The spike problem may cause the saturation of control input and even lead to the instability of whole system.In addition, for the schemes in Refs. 32,33, on the basis of using observer, an additional robust control scheme should be adopted to eliminate the effect of uncertainties, and thus the structures of controllers in Refs. 32,33 are very complex. In Refs.34,35,the authors have founded the spike problem existing in the Extend State Observer(ESO),and two kinds of nonlinear ESO with time-varying gain were developed in Refs.34,35.

Motivated by the above observations, a new Partial States Feedback Control(PSFC)scheme based on DSM and HGO is proposed for the FJM to eliminate the above problems. First,to avoid using the unmeasurable states, an HGO is proposed.Then,to simplify the control scheme,the HGO is also designed to estimate the uncertainties rather than designing an additional complex robust control scheme.Finally,to eliminate the spike problem of HGO, a novel Spike Suppression Function (SSF)is designed. Based on the reasonable selection of parameters,the SSF can suppress the initial spike estimation of HGO.The main contributions of this paper are summarized as follows:

(1) The spike problem in the existing HGO-based schemes is solved: A novel SSF is adopted to solve the estimation spike problem in the existing HGO such as the observers in Refs. 31–33. Since the spike problem can be avoided even when the observer gain is very high,a high observer gain can be adopted in the proposed scheme to guarantee the high control precision. Moreover, the SSF eliminates the spike problem by modifying the controller rather than the observer, and thus the solution to eliminate the spike problem of this paper is totally different from the existing schemes in Ref. 34,35.

(2) Only partial states of FJM need to be measured: The proposed method only needs the same measurement states as conventional RRM by using the HGO to estimate the unknown states.

(3) The structure of the proposed controller is simple: The unmeasurable states and uncertainties are estimated by HGO simultaneously. Then the uncertainties of FJM are compensated by using the estimation of uncertainties without requiring the additional robust control scheme such as the adaptive schemes used in Refs. 32,33. Thus,the structure of the proposed control scheme is simpler than that of the schemes in Refs. 32,33.

The remaining parts of this paper are as follows. In Section 2, the dynamic model, the design objective, and the motivation of this paper are expounded. The main results are presented in Section 3. In Section 3.1, a High-Gain Observer(HGO)is developed.In Section 3.2,a novel Spike Suppression Function(SSF)is developed,and then a dynamic surface controller based on HGO and SSF is proposed. In Section 4, a simulation verifies the effectiveness of the proposed HGO,SSF and controller. In Section 5, the conclusion of the whole paper is presented.

2. Problem formulation

2.1. Dynamic model of flexible joint manipulator

The flexible joint manipulator is shown schematically in Fig.1.The dynamic model of the Flexible Manipulator Control System (FMCS) can be described as follows:

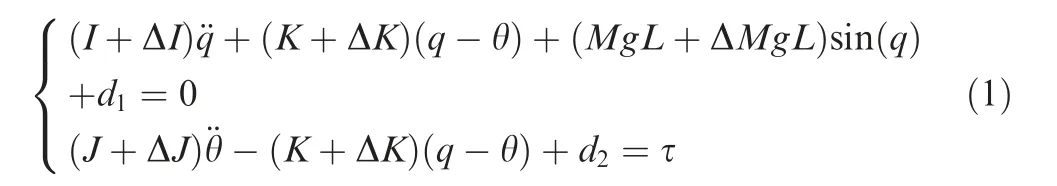
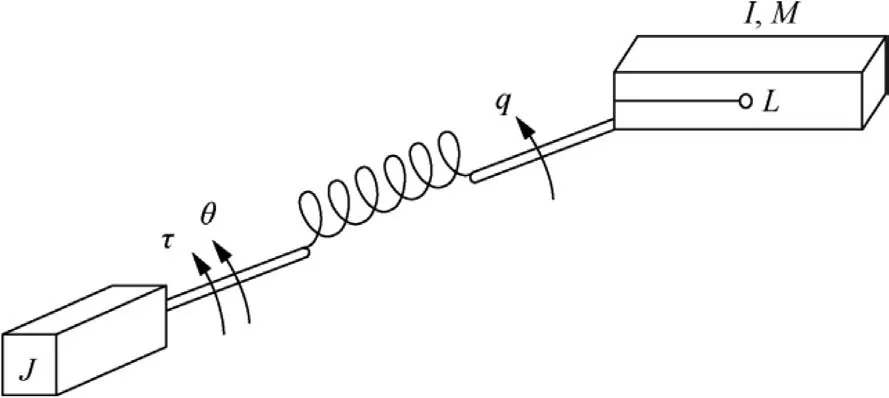
Fig. 1 Structure of flexible manipulator.

where q and ˙q are the rotation angle and angular velocity of link, respectively; θ and ˙θ are the rotation angle and angular velocity of motor,respectively;I and J are the moment of inertia of link and motor,respectively;M and L represent the mass and the distance between the joint and the centroid of the link,respectively;g is the gravity acceleration;K represents the elastic stiffness of the flexible joint; τ is the motor torque; ΔI, ΔK,ΔJ and ΔMgL represent the unmodeled dynamics of the FMCS; dand ddenote the disturbance from the environment.

2.2. Problem description and purposes of this paper

For the traditional control scheme for FJM in Refs.19–22,the link states q,˙q and the motor states θ, ˙θ are both assumed to be measurable,but the RRM controllers only need the link states qand ˙q. Thus, the measurement system for the controller in Refs.19–22 is much more complex than the measurement system for RRM. This motivates the first research topic of this paper, that is, designing a control scheme which only needs the same measurement states as RRM to simplify the measurement system of FJM.Thus,we have the following assumption:

On the other hand,from Eq.(4),it is clear that FJMCS is a typical mismatched uncertain system.To suppress the matched and mismatched uncertainties, the conventional control schemes in Refs. 32,33 for FJMCS need an additional robust scheme. Thus, the structures of the controllers in Refs. 32,33 are very complex. This motivates the third research topic of this paper, that is, avoiding using additional robust scheme.The motivation of this paper is summarized as follows:

(1) To avoid using the unmeasurable states, the unknown states will be estimated by designing an HGO in Section 3.1.

(2) To use the high observer gain, while avoiding the spike problem, a novel SSF will be proposed in Section 3.2.

(3) To suppress the uncertainties without using additional complex method,the proposed HGO is used to estimate not only the unmeasurable state but also the uncertainties.

3. Main results

3.1. High-gain observer

For the system (4), since θ and ˙θ are unmeasurable, the states xand xare unknown. Unknown states are combined with uncertainties to construct the new states. The new states are defined as p=x, p=x, p=x+Δ, p=x+ ˙Δand the uncertainty d=Δ+ ¨Δ-kΔ. Then the FJMCS (4)can be rewritten as

Remark 3.1. From Eq. (31), it can be known that the observer gain cshould be chosen large enough to ensure that the estimation error is small enough. Thus, the proposed observer(16) also is a typical HGO. The undesirable spike problem may be caused by the high observer gain as mentioned above in Section 1.2. To solve this potential problem, a novel Spike Suppression Function (SSF) will be proposed in the following control design.

3.2. Dynamic surface controller based on HGO and SSF

Based on the estimate states ^pand ^p, and the estimation of uncertainty ^p,a DSM control scheme for the FJMCS(12)will be proposed by the following four backstepping steps. And a novel SSF is adopted in the proposed controller to deal with the aforementioned spike problem of HGO.

Step 1.Define a tracking error as s=p,the virtual control of pis designed as

Remark 3.2. As mentioned in Section 2.2, the spike problem of HGO can be caused by a high observer gain cif p(0 )≠^p(0 )in the initial small time period. From Eq. (38), it is clear that the spike values of HGO can be taken into the control input by ^p,p, ^p, ^p, ˙pwhich contain the outputs of HGO directly or indirectly. Thus, for the proposed controller,χ(t),χ(t),χ(t)andχ(t) are adopted to suppress the spike values of ^p-p,^p,^pand ˙p. From Eq. (39), it can be known that χ(t) is small enough in the initial small time period by choosing the parameters reasonably, and the spike values taken by ^p, p,^p, ^p, ˙pcan be suppressed by the proposed SSF.Remark 3.3. Since χ(t )→1 if t →∞,the stability and control precision of the proposed controller will not be affected by the SSF. The detail stability and control precision analysis of the proposed controller with SSF will be given in Theorem 2.

Before giving Theorem 2, the following assumption which is commonly used in DSM (for example, in the Section 3.2 in Ref. 23, the author assumed that the derivative of virtual control input is bounded as a positive constant) should be assumed to be valid throughout this paper:

From Eqs. (33), (35) and (37), we have

Remark 3.5. From the proof of Theorem 2, it is clear that the stability and control precision are not affected by the proposed SSF.

4. Simulation results

In this section, to illustrate the effectiveness of the proposed control scheme, the mathematical simulation is presented.Consider that the parameters for FJMCS system (1) are selected as

Then,consider the following two control schemes in Case 1:

Fig.3 show the above schemes.From Fig.3(a),for the controller without SSF,it is clear that the tracking error converges slowly and an undesirable large overshoot phenomenon can be observed. As mentioned before, the reason is that the spike problem of HGO can be caused by choosing a large gain if p(0 )≠^p(0 ).And the spike values from HGO can be taken into the control input, directly or indirectly. The spike values from HGO can be observed from Figs. 3(c)–3(g). And Fig. 3(b)shows that the control input of the controller without SSF is saturated under the spike value. From Fig. 3(a) and (b), it is also clear that the spike values can be suppressed effectively by the proposed controller with SSF.An excellent control performance still can be guaranteed by the proposed controller with SSF. From Fig. 3(h), it can be seen that the SSF χ(t ) is small enough in the initial time, and thus the spike values can be suppressed. And χ(t )→1 if the time is large enough,and then control precision will not be affected by the SSF.

Case 2. (Control performance of partial states feedback). To show the performance of the proposed partial states feedback scheme, the following two controllers are compared in this case:

(2) Full State Feedback Controller (FSFC):It is assumed that all states are measurable, which means that it is unnecessary to design the observer to estimate the unmeasurable states. Then, only based on the conventional DSM, the FSFC for FJMCS (4) can be designed as

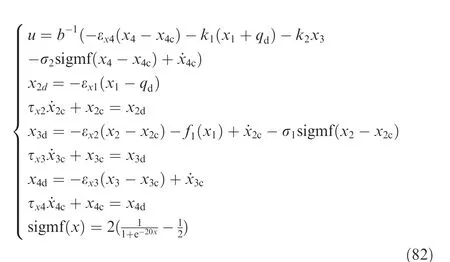
where the parameters are chosen as

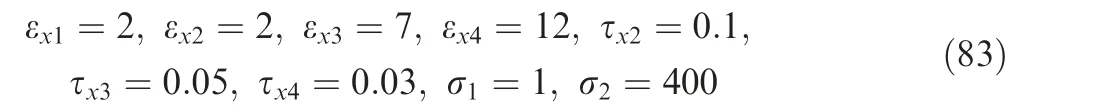
And sigmf(∙) is used to avoid the chattering problem and suppress the uncertainties. The explanation of sigmf(∙) can be found in previous work. The unmodeled dynamics and the disturbance from the environment are chosen as in Eq.(77).

The above PSFC and FSFC are used for tracking two kinds of desired angles q=1 rad and q=cos(t) rad, respectively.The simulation results for Case 2 are shown in Fig. 4. From the simulation results, it is clear that both the conventional FSFC and the proposed PSFC can guarantee the fast and accurate convergence of tracking error for the two kinds of desired angles. Thus, compared with the conventional full states feedback scheme, the proposed method of this paper can achieve similar excellent control performance even with partial states feedback.

Case 3. (Anti-disturbance performance of the proposed partial states feedback scheme). To show the anti-disturbance performance of the propose scheme, the following three kinds of unmodeled dynamics and disturbances from the environment are chosen as

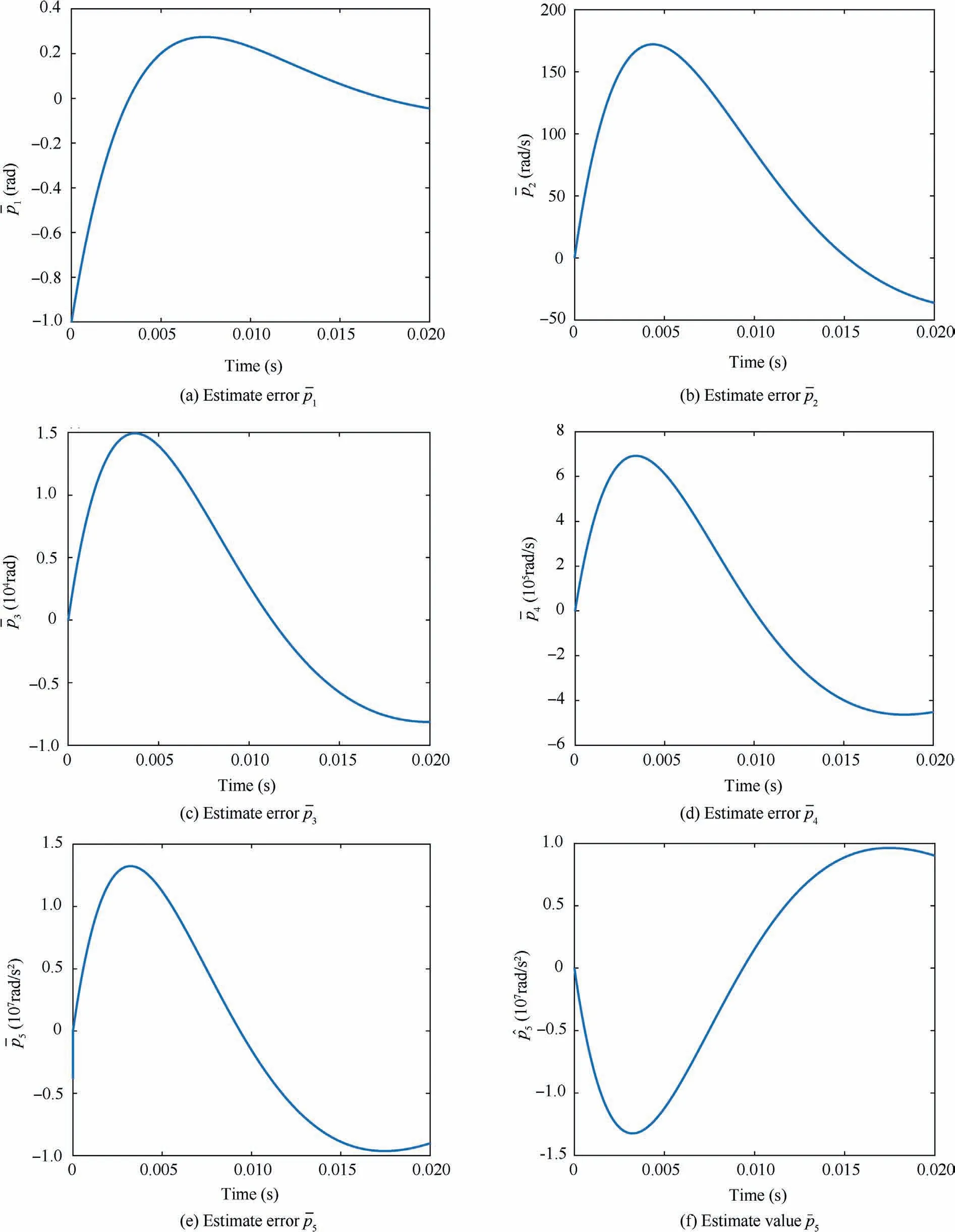
Fig. 2 Simulation results of Case 1 (u=0).

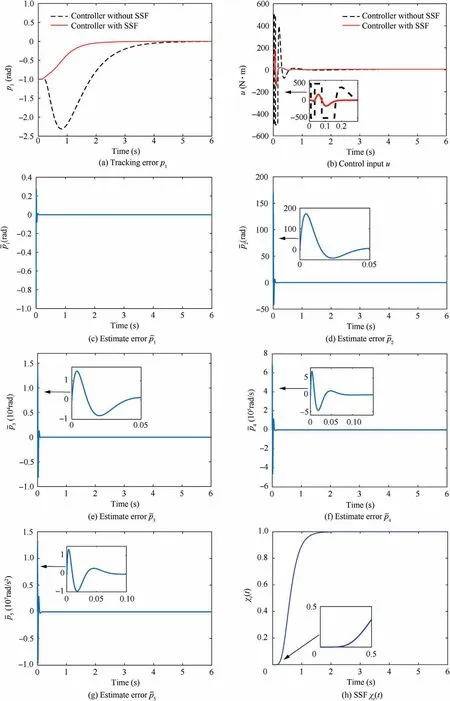
Fig. 3 Simulation results of Case 1 (u≠0).

Fig. 4 Simulation results of Case 2.

Fig. 5 Simulation results of Case 3.

(1) Small amplitude and low frequency

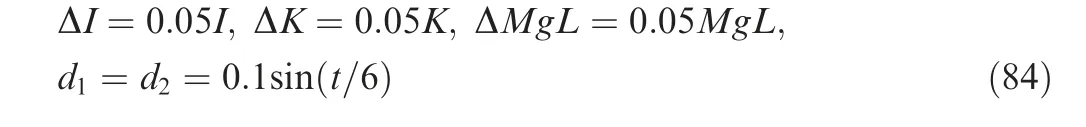
(2) Large amplitude and low frequency

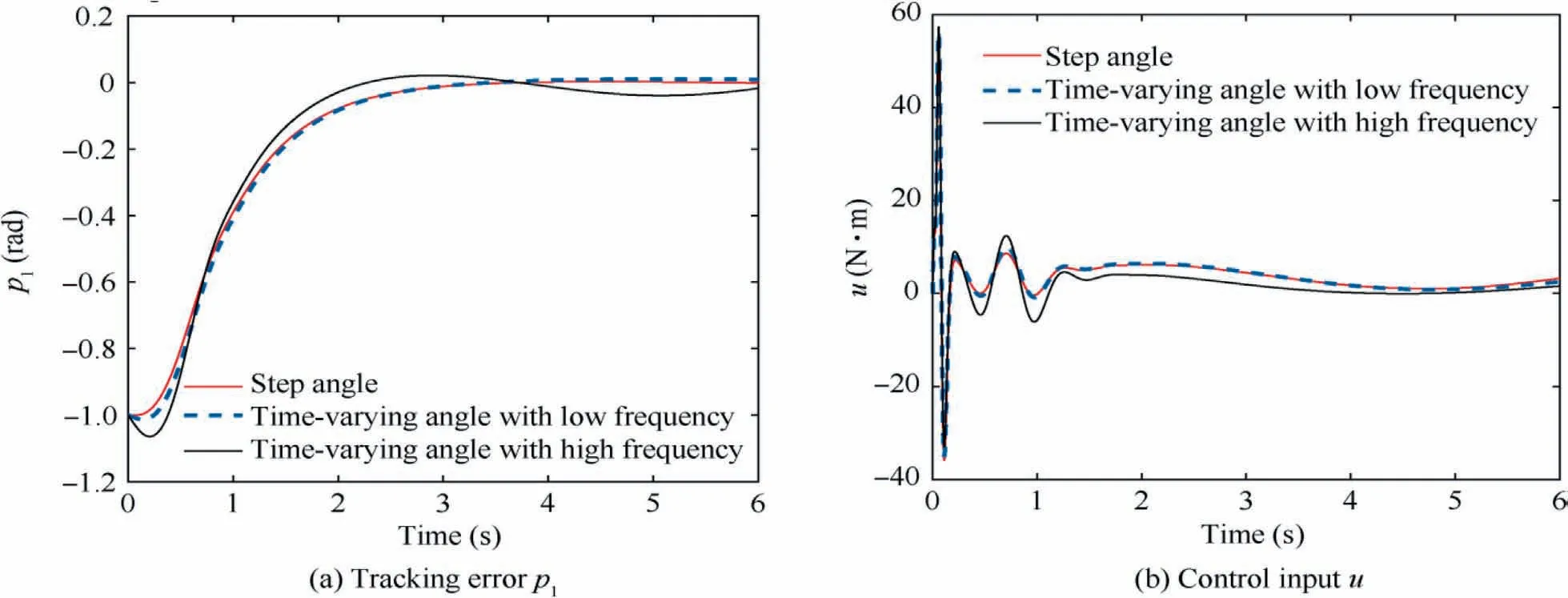
Fig. 6 Simulation results of Case 4.

(3) Large amplitude and high frequency

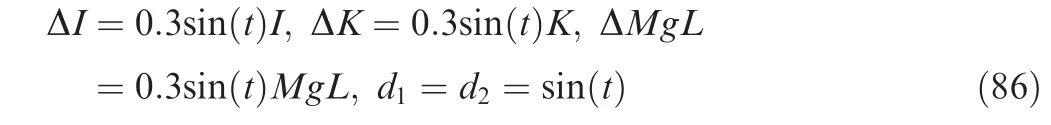
Fig.5 shows the simulation results for Case3.From Fig.5,it is clear that the proposed PSFC can achieve good antidisturbance performance for the three kinds of unmodeled dynamics and disturbances.

Case 4. (Tracking performance of the proposed partial states feedback scheme for different desired rotation angles). To show the tracking performance of the proposed scheme for different desired rotation angles, the following three kinds of desired rotation angle are chosen:

The unmodeled dynamics and disturbances from the environment are chosen as in Eq. (86). Fig. 6 show the simulation results for Case4. From Fig. 6, the proposed PSFC can guarantee that the tracking errors converge to a small neighborhood of zero for the three kinds of desired rotation angle.

5. Conclusions

In this paper, a novel PSFC is proposed for the FJM with unmeasurable system states based on DSM and HGO. The main contributions here are that:

1) The proposed method only needs the same measurement states as conventional RRM;

2) The estimation spike problem in the existing HGObased control is solved by developing a novel SSF;

3) Without using additional complex robust method which is wildly used in the conventional PSFC schemes, the proposed control scheme can still suppress the uncertainties by using HGO to estimate the unmeasurable states and uncertainties simultaneously. Moreover, the mathematical simulation results demonstrate that the performance of the proposed controller is excellent.Finally, experiment will also be carried out in the later research, and theoretical results will be compared with experimental data.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was co-supported by Natural Science Foundation of Shaanxi Province (Nos. 2020JM-131, 2020KW-058), the Key Research and Development Program of Shaanxi, China(Nos.2019GY-025,2018GY-091),Xi’an Science and Technology Plan Project, China (No. 2020KJRC0134), and Special Fund for High Level Talents of Xijing University, China(No. XJ20B07).