AGA8-DC92和GERG-2008状态方程在天然气密度测算中的精确度比较

叶喆

浙江浙能天然气运行有限公司（浙江 杭州 310052）

1 概述

密度是天然气行业重要的物态数据，广泛应用于天然气的勘探开发和计量结算领域。通过实验仪器获取天然气在不同成分组成、温度和压力下密度数据的做法非常耗时，增加了天然气密度等物态数据在工程应用时的成本。基于经验数据的高精度数学测算模型获取天然气密度是目前天然气工业最为常见的做法。1992 年国际标准化组织天然气技术委员会及分析技术分会提出了两种高精度天然气密度测算方法，分别是AGA8-DC92 和SGERG-88方程[1]。在AGA8-DC92和SGERG-88方程的适用范围内，它们对样品的测算值与实测值之间的偏差基本保持在1%以下，优于Peng-Robinson、Redlich-Kwong-Soave 状 态方程 以 及Lee-Kesler 对应态方程偏差5%～20%的水平，得到更广泛的应用。

AGA8-DC92 是由美国燃气协会提出的测算方法。GB/T 17747.2—2011《天然气压缩因子的计算第2 部分：用摩尔组成进行计算》采用了AGA8-DC92作为其标准核心，适用于温度在263～338 K，压力最高至12 MPa状态下的天然气压缩因子测算[2]。

AGA8-DC92 在工程应用中的优点是所需基础数据少以及在适用范围内较高的测算结果精度。当温度在290～350 K，压力低于30 MPa时，对于主要成分为甲烷的天然气，AGA8-DC92对压缩因子的测算值与实测值之间偏差在0.1%左右。在声速下温度超过270 K时，天然气热值测算误差在0.2%左右，而等压热容和等压焓的偏差大致在1%[3]。

AGA8-DC92 的缺点也明显。首先，在适用温度范围之外测算结果的精确度就大幅下降，当高于压力12 MPa 时压缩因子不确定性大于0.1%，限制了AGA8-DC92 的进一步应用。其次，在较低温度下天然气含有大量氮气、二氧化碳、乙烷或其他重烃时，AGA8-DC92 对热力学性质的测算误差将大幅增大。特别是在含有更高摩尔分数的重烃成分时，即便在适用温度压力范围内，通过实测和AGA8-DC92 测算获得的两组热力学性质数据之间的差值也将变大[4]。

SGERG-88 测算方法基于GERG-88 标准维里方程，是由欧洲天然气研究组提出的一种用于天然气和其他混合物的宽域状态方程。GB/T 17747.3—2011《天然气压缩因子的计算第3部分：用物性值进行计算》采用了SGERG-88测算方法，适用温度和压力的范围与AGA8-DC92 基本相同，优点在于其测算的高精确性和不依赖物性外的其他数据，缺点在于其相较于AGA8-DC92方法计算过程和计算工作量大[4-5]。

经过实践和理论的发展，欧洲天然气研究组推出了一种基于Helmholtz自由能的GERG-2004状态方程[6]。此后，欧洲天然气研究组在GERG-2004 状态方程18个组分参数的基础上，又加入3个新组分参数，形成了GERG-2008方程[4]。GERG-2008方程的数据库包含了三万多天然气随机组合样本的关系参数[9]。

GERG-2008 方程在温度为90～450 K，压力在35 MPa以下的区间内，测算值与实测值之间的偏差在0.05%以下；当温度高于250 K 且压力小于30 MPa 时，GERG-2008 的测算与实测偏差在±（0.05～0.1）%[7]。对于测算声音在气相中的传导速度，压力不大于11 MPa，温度处于250～350 K时，与实测声速的偏差基本分布在0.2%～0.5%[8]。对于凝析物较多的天然气，算得气相密度偏差在±（0.1%～0.3%），测算等压热容时，对于天然气或其他气相混合物测算偏差大致分布在1%～2%。GERG-2008 方程对较为复杂天然气富气，特别是在氢气、氮气、二氧化碳、乙烷以及丁烷等重质成分较多，甚至含有氧气时的适用性和测算精度较高。对饱和液体密度的测算精度偏差在±（0.1%～0.5%），对液体的等压焓的测算偏差在±（0.5%～ 1%），对蒸汽压的测算偏差在±（1%～3%）[6-9],温度在270 K 以上时，对压缩因子的测算偏差在0.7%以下[9]。即温度在60～700 K，压力不超过70 MPa 时，GERG-2008 对均相气体、液体、超临界以及在气液平衡状态的整个流动相中还能适用，可较为准确地测算出气相和类似气体的临界密度、声速和焓差[4，6-7]。

在实际勘探开发和计量结算中，应用更高测算精度的方法将有助于提高油气的采收率，减少天然气贸易计量中的纠纷。温度压力适用范围更宽，对不同油气组分兼容性更强的高精度数学测算模型将更易受到石油与天然气工程师和天然气贸易计量结算双方的青睐[6]。针对AGA8-DC92 和GERG-2008状态方程的应用特点，以及在测算天然气密度上的精确度进行比较和讨论。

2 AGA8-DC92方程

AGA8-DC92方程一般表示为[2]：

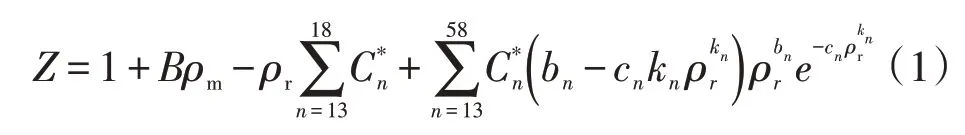
式中：Z是压缩因子；B是第二维里系数；ρr是对比密度；是温度和组成的函数系数；bn、cn、kn和un是常数参量。ρm是摩尔密度，kmol/m3；p是绝对压力，MPa。

式中：an是常数；xi和xj分别是气体混合物中的组分i和j的摩尔分数；是混合物交互作用系数；En,ij是第二维里系数的二元能量交互作用参数，均为无量纲数，T是温度为K。Ki和Kj分别是组分i和j的体积参数，(m3/k mol)1/3。

式中：Gij是二元定位参数；Qi和Qj分别是组分i和j的四级参数，Fi和Fj分别是组分i和j的高温参数，Si和Sj分别是组分i和j的偶极参数，Wi和Wj分别是组分i和j的组合参数。

式（3）中，G是混合定位参数，Q是四级参数，F是混合高温参数，U是能量参数，gn、qn和fn是常数参量，无量纲。其中，G、Q、F和U可分别表示为：

式中：Eij是第二维里系数的二元能量参数，K；M是摩尔质式量，kg/k mol；K是体积参数，(m3/k mol)1/3；二元定位参数Gij无量纲。分别表示为：

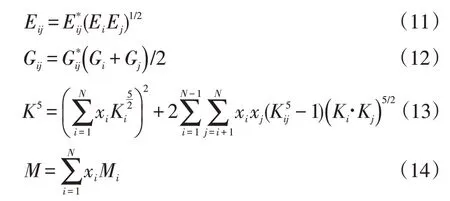
式中:Ei和Ej分别是组分i和j的特征能量参数，K；Mi是组分i的摩尔质量，kg/k mol；E*

ij是第二维里系数的二元能量交互作用参数；Gi和Gj分别是组分i和j的定位参数，无量纲。

AGA8-DC92计算方法的流程如图1所示，先通过输入热力学温度T（K），绝对压力p（MPa）和混合物中各组分的摩尔分数xi；计算状态方程系数B和（n=13～58），两者均取决于T和xi；利用改写的状态方程迭代求解摩尔密度ρm得到压力p；当迭代求得的压力和初始输入的压力在规定的收敛范围内相一致时，即获得测算的压缩因子。

图1 AGA8-DC92计算方法程序流程

3 GERG-2008方程

GERG-2008方程一般表示为[4]：

式（15）由两部分组成，即理想Helmholtz自由能αo和剩余Helmholtz自由能αr。T为混合物的温度，K；ρ为混合物的密度，kg/m3。

式中:αo

oi为理想Helmholtz自由能；Fij为二元调节因子；xi和xj分别为混合物中i、j组分的摩尔分数；为对比Helmholtz 自由能；为二元对比Helmholtz自由能。

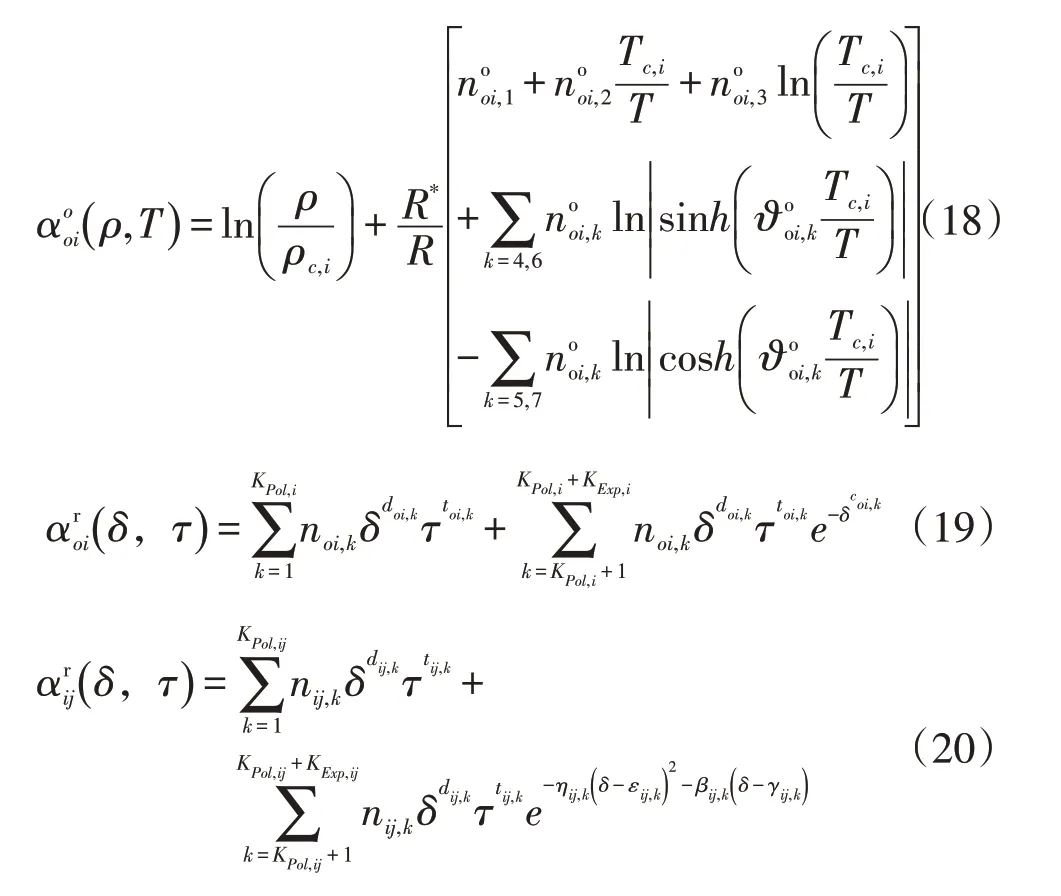
式中：R*为理想气体常数，8.314510 J/mol·K。

各式中δ为混合物的对比密度，kg/m3；τ为对比温度的倒数，1/K。Tc,i和ρc,i为组分i的临界温度和临界密度，单位分别为K 和kg/m3。nij,k为组分i和j之间相互作用关联因子，和分别为对比Helmholtz自由能的计算因子和参数，doi,k、toi,k、coi,k，以及dij,k、tij,k、ηij,k、εij,k和γij,k为组分i和j间相互作用的指数参数，无量纲。其中，δ和τ分别表示为：

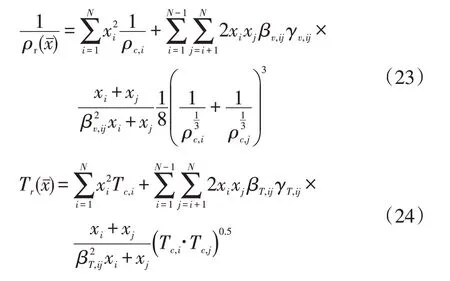
式中：βv,ij和βT,ij分别为等容和等温下组分i和j之间的摩尔二元参数，γv,ij和γT,ij分别为等容和等温下组分i和j的二元定位参数，无量纲。ρc,i和ρc,j、Tc,i和Tc,j分别为组分i和j纯物质的临界密度和温度，单位分别为kg/m3和K。

GERG-2008 方程的主要计算步骤是将混合物的已知温度、压力和各组分的摩尔分数xi代入方程后，经多步迭代得到混合物的摩尔密度ρm，具体步骤如图2所示。

图2 GERG-2008计算程序流程

4 AGA8-DC92 与GERG-2008 的 测算精确度比较

通过整理的相关文献的研究结论数据，用AGA8-DC92与GERG-2008对同一组分的天然气在相同温度压力条件下的测算值与实测值偏差的绝对值之间差值的分布情况，来比较两种方法之间精确度的优劣性。比较测算密度所用的偏差差值计算公式如下：

当偏差差值数据呈正值时，说明AGA8-DC92的测算偏差较大，相比之下GERG-2008的测算精确度较高；当偏差差值数据呈负值时，说明GERG-2008 的测算偏差较大，而AGA8-DC92 的测算精确度较高。

为研究卡塔尔北方气田天然气密度性质，Mert Atilhan 分 别使用AGA8-DC92 和GERG-2008 两种方法测算了天然气QNS-S1～QNS-S4 的摩尔组成（表2）及在不同温度压力条件下的密度值。在压力超过45 MPa 时测算密度，AGA8-DC92 的偏差在±0.05%，而GERG-2008的偏差在±0.02%。整理的偏差差值分布情况分别如图3、图4、图5[10]所示。

图3 测算QNG-S1密度的偏差差值分布（等温下）

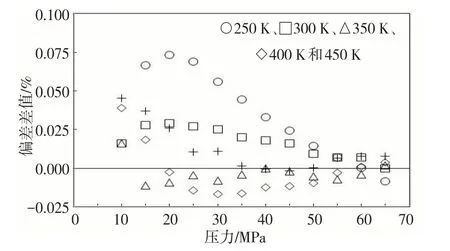
图4 测算QNG-S2密度的偏差差值分布（等温下）

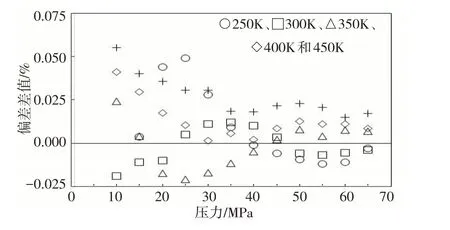
图5 测算QNG-S3密度的偏差差值分布（等温下）

Hernández-Gómez 等研究了天然气样品BAMG 420 和CCQM K 118（摩尔组成见表2）在温度为260～350 K，压力从1 MPa 逐步提升至20 MPa 时的密度变化[7]。AGA8-DC92 和GERG-2008 两种方法对其密度测算的偏差差值分布如图6和图7所示。

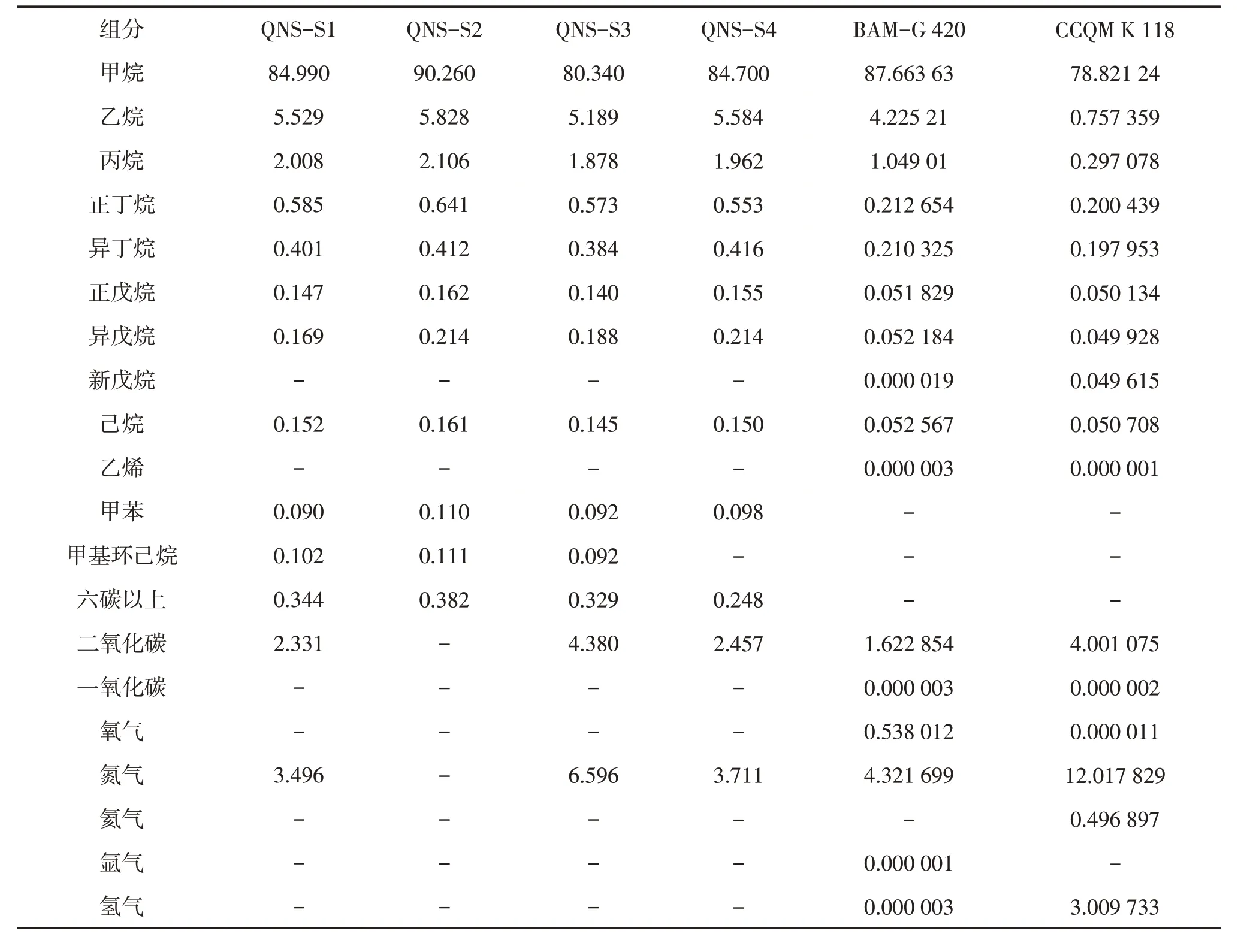
表2 天然气样品的摩尔组成 /%

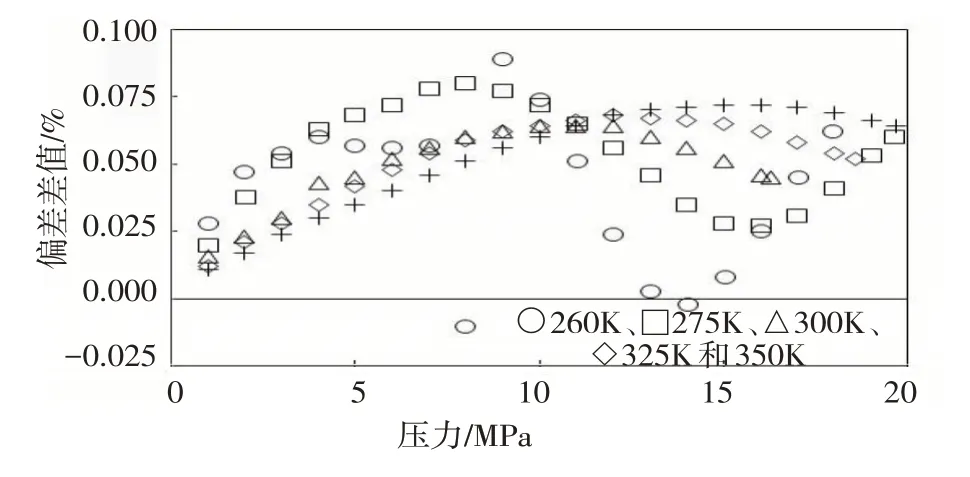
图6 测算BAM-G 420密度的偏差差值分布（等温下）

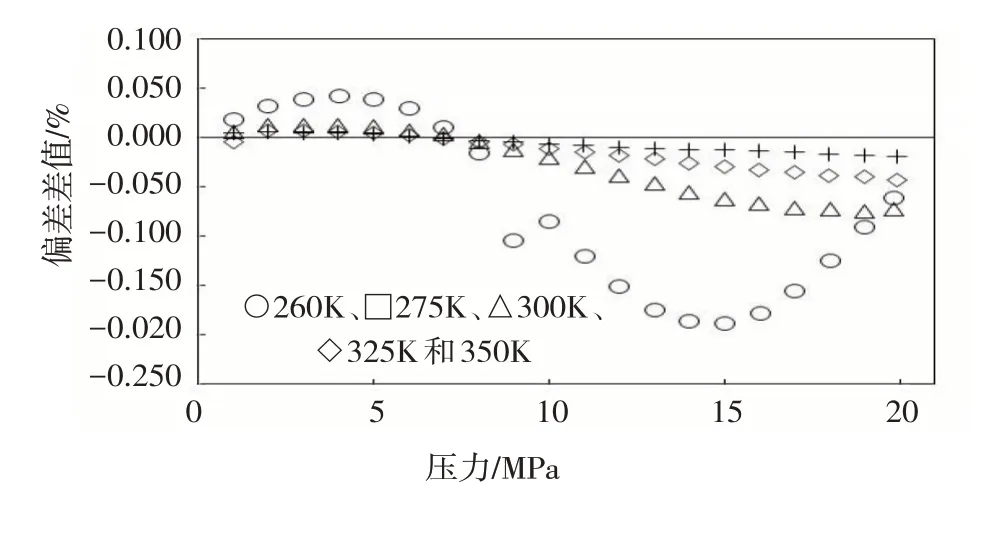
图7 测算CCQM K 118密度的偏差差值（等温下）

总结分析以上6组不同样品实验获得的偏差差值分布情况，呈正值的数据点有300 个，占总体429个数据点的69.9%，负值的数据点有129 个，占总体的30.1%，这表明GERG-2008 的总体精确度高于AGA8-DC92。

AGA8-DC92和GERG-2008两种方法偏差差值数据的正负分布规律与各组分差异之间并无特别的规律可循，表明在面对惰性或重质组分时两种方法之间没有明显优劣之分。在低温低压的区间内偏差差值多呈正值，表明GERG-2008 的测算精度相对较高。在温度为300～450 K，压力逐渐增大至65 MPa时，两种方法的测算精确度差异明显变小[11-12]。AGA8-DC92对密度的测算偏差总体要高于GERG-2008约30%。

由于GERG-2008 测算值与实测值的偏差多呈负数，所以相应获得的标准流体容积要小于AGA8-DC92。因此，使用GERG-2008 计量结算有利于天然气交易的下游，受到交易结算中买方的青睐[13]。

5 结论

数据结果表明，GERG-2008对密度的测算精度总体优于AGA8-DC92，且适用温度压力范围更大。在低温低压的同等条件下，GERG-2008的测算精度明显高于AGA8-DC92。在面对惰性或重质组分较多的样品时，AGA8-DC92 和GERG-2008 之间没有明显的优劣之分。在各自温度压力适用范围的相互重叠区间内，两种方法之间的测算精确度差异较小。