一种转子系统基础脉冲激励作用下响应的计算方法研究

摘要：以基础脉冲激励下的转子系统为研究对象，对转子系统进行梁单元有限元建模，对基础脉冲激励运用时域模拟法进行了模拟，运用Newton-Raphson法求解轴承非线性力和转子系统运动微分方程，建立了一种高效求解含非线性转子系统基础脉冲激励作用下响应的计算方法。开展基础脉冲激励下转子—轴承系统瞬态响应特性试验研究，对分析模型和分析方法的有效性和正确性进行了验证。

关键词：基础脉冲激励;非线性求解;转子动力学;瞬态响应

中图分类号：V231.96    文献标志码：A    文章编号：1671-0797（2022）06-0074-05

DOI：10.19514/j.cnki.cn32-1628/tm.2022.06.021

1    研究背景

固定翼舰载机弹射起飞和拦阻着舰过程中，发动机转子系统会承受基础脉冲激励作用。考查航空母舰发展进程，固定翼舰载机起飞方式从滑跃起飞到蒸汽弹射再到未来的电磁弹射，发动机转子系统所受的基础脉冲激励载荷越来越大。固定翼舰载机弹射起飞时在70～90 m长的飞行甲板上，经历2～3 s时间加速到接近300 km/h的速度，此时发动机的纵向基础过载峰值达到4g～5g[1]。近年来，舰载机电磁弹射技术研究得到了快速发展，已处于实验验证阶段[2]。电磁弹射周期更短，弹射力更大，发动机的基础过载峰值也更大，因此当下迫切需要研究基础脉冲激励作用下转子系统瞬态响应计算方法，为舰载机发动机的安全性设计提供理论支撑。

2    转子系统梁单元有限元建模

同傳统方法相比，运用梁单元有限元法进行转子系统建模通用性好，建立的转子模型单元少，可以提高计算效率[3]，方便对转子系统非线性和瞬态响应进行分析。Timoshenko梁单元示意图如图1所示，考虑剪切变形的梁单元示意图如图2所示。

图1中，每个单元包含2个节点，每个节点4个自由度，分别为x、y方向的平移自由度和绕x、y轴的转动自由度。x、y方向的平动位移分别用u和v表示;绕x、y轴的角位移分别用φ和θ表示;xOz平面上，y轴垂直纸面向外;yOz平面上，x轴垂直纸面向里;下标e1、e2分别表示单元的第1个节点、第2个节点;le表示单元的长度;ξ为0～le中间任意一点。

假设单元轴段为各向同性的圆截面轴，且单元内部横截面面积处处相同;单元轴段材料为线弹性材料，弹性模量表示为Ee;单元内任意横截面在变形后仍为平面，但不一定与中性轴垂直，即考虑剪切变形。单元的节点位移向量可写成式（1）：

式中：Ω为转子自转角速度;Ps为转子系统所受的基础冲击载荷向量;M、C、G、K分别为系统的惯性矩阵、阻尼矩阵、陀螺矩阵和刚度矩阵，此处的系统刚度矩阵仅包含转子轴的刚度，支承的非线性刚度包含在了非线性力Fbearing之中，放在了等式右端。

5.2    系统微分方程求解

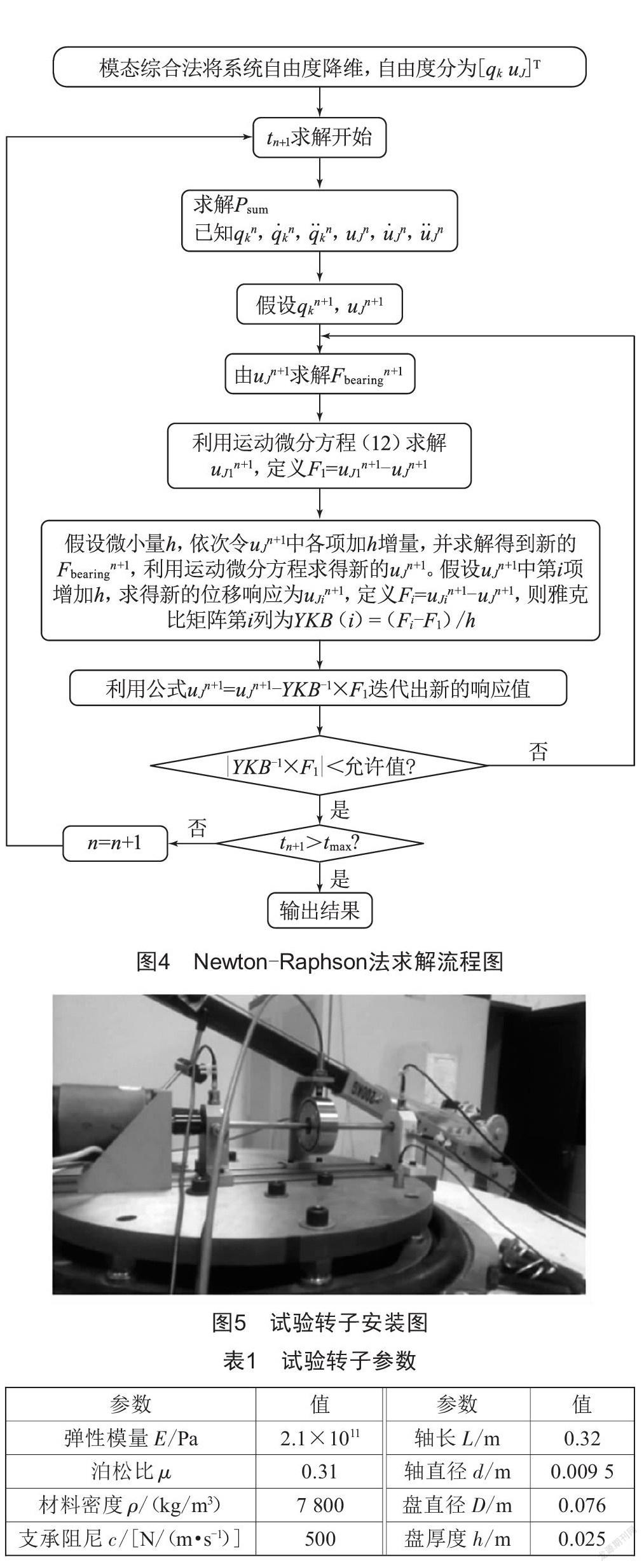
式（12）中的项Fbearing是与位移相关的非线性力项，因此式（12）为非线性方程组。对于非线性方程组，通常有不动点迭代法和Newton-Raphson法。Newton-Raphson法与不动点迭代法相比计算较为复杂，但由于其在方程根附近为平方收敛，因此具有收敛速度快的优点。本文选用Newton-Raphson法进行微分方程求解，求解流程如图4所示。

6    试验验证

6.1    试验设计

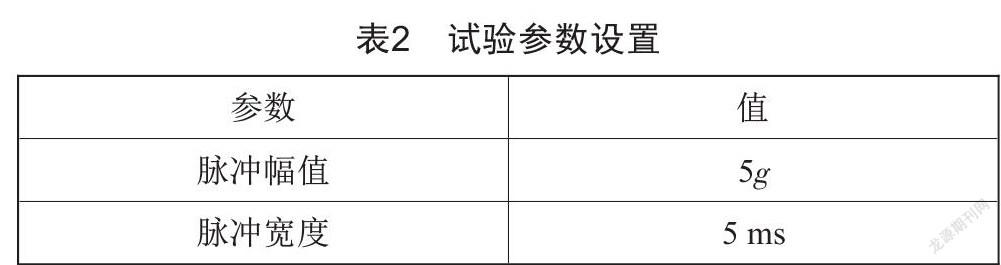
采用Jeffcott转子试验器验证本文的理论计算，试验转子及安装如图5所示，转子系统参数如表1所示。试验转子两端为轴承支承，由电机驱动转轴。在盘的相互垂直的两个方向上安装电涡流位移传感器，在支承的水平方向和竖直方向安装加速度传感器。位移和加速度信号测量装置如图6所示，数据采集界面如图7所示，振动台及控制软件如图8所示。

转子系统基础脉冲激励选用苏州东菱振动试验仪器有限公司的ES-50W-445型电动振动试验系统（图8）（以下简称“振动台”），试验转子通过底座安装在振动台上。振动台最大负载为800 kg，最大加速度为1 000 m/s2，试验转子系统（含底座）重量为40 kg，脉冲加速度幅值最大设置为6g（58.8 m/s2），试验装置满足试验需求。

本次试验选用半正弦脉冲形式，图9为振动台实际输出的波形图，其中浅绿色波形表示在控制软件中设置的理想波形，深绿色波形表示实测输出信号。可以看出，振动台实际输出的加速度脉冲激励与设定值吻合较好，对于试验中设定的不同脉冲宽度、脉冲幅值、脉冲激励形式均能按照设定值进行加载。

6.2    结果对比

按表2所示参数进行试验，试验中控制转速为变量，转速分别选取1 000 r/min、2 000 r/min、4 000 r/min，试验结果与仿真结果对比如图10所示。

通过分析图10转速从1 000 r/min到4 000 r/min变化时盘垂直方向响应的趋势发现，盘的垂直方向响应是基础脉冲激励下的响应与盘的不平衡响应的叠加，基础脉冲激励后盘的响应由基础脉冲激励响应主导，而后，在脉冲衰减的过程中，基础脉冲激励引起的响应逐渐减小，盘的不平衡响应越来越占据主导位置。这一趋势在高转速下更加明显，因为转速越高，盘的不平衡响应越大，与基础脉冲激励响应越接近，此时基础脉冲激励响应与不平衡响应的叠加效果越明显。

并且，随着转速增加，基础脉冲激励响应衰减所需的波的个数减少，这是因为转速频率变大，越来越接近于基础脉冲激励的频率，此时也会呈现脉冲激励响应与不平衡响应越来越合拍的趋势，衰减波形越来越纯净，脉冲激励造成的瞬时紊乱效果越来越不明显。

另外，仅转速变化时，盘的垂直方向响应幅值几乎不变，即转速几乎不影响对转子系统基础脉冲激励作用下的响应幅值。

盘受基础脉冲激励响应的以上变化趋势在试验和仿真结果中都有较好的体现，验证了本文模型和分析方法的正确性。

7    结语

本文围绕含非线性支承的转子系统在基础脉冲激励下的瞬态响应特性分析方法开展研究。结合转子系统梁单元有限元建模和基础脉冲激励时域模拟法建立了转子系统运动微分方程，并运用Newton-Raphson法对转子系统响应进行求解，该方法方便可靠，通用性强。最后，通过转子系统基础脉冲激励试验验证了分析方法的正确性。

[参考文献]

[1] 聂宏，房兴波，魏小辉，等.舰载飞机弹射起飞动力学研究进展[J].南京航空航天大学学报，2013，45（6）：727-738.

[2] DIMENTBERG M F.Random vibrations of a rotating shaft with non-linear damping[J]. International Journal of Non-Linear Mechanics，2005，40（5）：711-713.

[3] 王飞.挤压油膜转子系统建模方法研究及动力特性分析[D].南京：南京航空航天大学，2018.

[4] 纪进召，贺少华，吴新跃，等.滑动轴承—转子系统基础冲击响应研究[J].造船技术，2010（5）：16-19.

[5] 沈荣瀛，张智勇，汪玉.船舶推进轴系冲击响应[J].中国造船，2000，41（3）：76-81.

[6] 贺少华，吴新跃.一种转子系统冲击响应的计算方法：平均速度Newmark-Riccati传递矩阵法[J].应用力学学报，2010，27（4）：823-829.

收稿日期：2022-01-05

作者简介：杨泽东（1992—），男，甘肃金昌人，硕士研究生，助理工程师，研究方向：航空发动机结构与强度。