考虑储能充放电的孤岛微电网经济优化模型

江宏玲

（安徽省水利部淮河水利委员会水利科学研究院，合肥 230088）

0 引 言

微电网是一种十分有效的可再生能源利用和管理方式，得到了非常多的应用。越来越多的高渗透可再生能源发电系统（Renewable generations system，RGS）被集成到微电网能源发电系统（Microgrid generations system，MGS），这对系统的经济运行提出了新的技术挑战［1］。由于MGS中存在多个间歇RGS和波动负荷，MGS的经济运行涉及供需双方的最优调度。特别是在孤岛模式下，MGS必须保持自身功率供需平衡，才能实现可靠、经济的运行。

文献［2］中提出一种基于改进粒子群算法的MGS集中控制优化模型。文献［3］中提出一种改进遗传算法来最小化MGS的操作成本。文献［4］中将一种快速、可靠的线性规划方法应用于MGS的经济调度，在满足各种资源约束的前提下，使运行成本最小化。上述文献中的集中优化方法通常是不灵活的，容易受到单点故障的影响。这些方法大多需要复杂的通信网络来采集全局信息。这对通信有很高的要求，甚至可能导致隐私泄露［5］。相比之下，分布式优化具有灵活、可靠和保密性等优点，已成为MGS经济调度的一种很有前景的方案［6］。文献［7］中提出一种基于分布式优化的次梯度算法来最小化MGS系统的发电成本。但迭代过程涉及发电成本信息，导致密钥隐私泄露问题。这可以通过基于交替方向乘数法（Alternating direction multiplier method，ADMM）的分布式经济调度模型来解决，该模型只需要交换电能信息，就可以将孤岛MGS的成本降到最低［8］。然而，所提模型的调度结果可能并不准确，因为它们都是在长时间内实现的。MGS的经济调度不仅可以最小化系统的总发电成本，而且还可以确保MGS的最大输出能力［9］。针对这些因素，文献［10］中建立了基于一致性算法的孤岛MGS实时经济优化模型。该模型最大化了MGS的输出，同时系统的运行成本达到最小。但是，没有充分考虑储能系统（Energy storage system，ESS）参与孤岛MGS经济调度的情况，可能存在供电不足、能源浪费等问题。ESS系统具有时间耦合的特性，使得其实时输出模型的建立变得困难。基于这一考虑，本文提出了一种分布式优化方法，用于孤岛MGS的实时经济调度。

1 系统模型

本文将孤岛MGS中的每个参与单元建模为一个代理，每个代理可以与相邻的代理进行通信（电价、电能等信息）。孤岛MGS由5个代理组成：一个ESS代理、一个常规发电机系统（Conventional generators system，CGS）代理、一个RGS代理和两个负载（load）代理。在多代理系统框架下，CGS和ESS被认为是可调度的代理。相比之下，RGS不被认为是可调度的代理，因为RGS如风能和光伏（Photovoltaic，PV）能源通常是随机和间歇的。

1.1 ESS代理实时经济模型

ESS是消除RGS功率波动、降低能源平均价格的关键技术。在此基础上，提出了一种适用于实时调度的ESS收益模型。

考虑到过去能源市场价格的矢量πT，t：

式中：下标T为过去某一段时间；ΔT为设定在T小时内的一段固定时间差值；下标t为在T小时内的某一t时刻。因此，ESS代理在过去T小时内在t时刻的平均电价πE，mean，t可以定义为：

式中，下标E为ESS代理，mean表示平均。如果ESS代理以πE，t为t时刻ESS代理的实时电价，用π表示存储的电能在将来的某个t时刻的转售价格。那么当π＞πE，t时以π转售，ESS代理就可以获得收益。为便于计算，在矢量πT，t中，用π表示高于πE，mean，t的所有能源价格的平均值。此外，充电时应考虑电池折旧和设备运行成本。因此，ESS充电时的输出函数UE，ch，t和成本函数CE，ch，t可以表示为：式中：PE，ch，t为t时刻ESS代理的充电功率；π为矢量πT，t中大于πE，mean，t的第i个电价；n为矢量πT，t中大于πE，mean，t的数字。CE，ch，t为时间t时刻电池折旧和设备运行成本；aE、cE为ESS的成本系数。

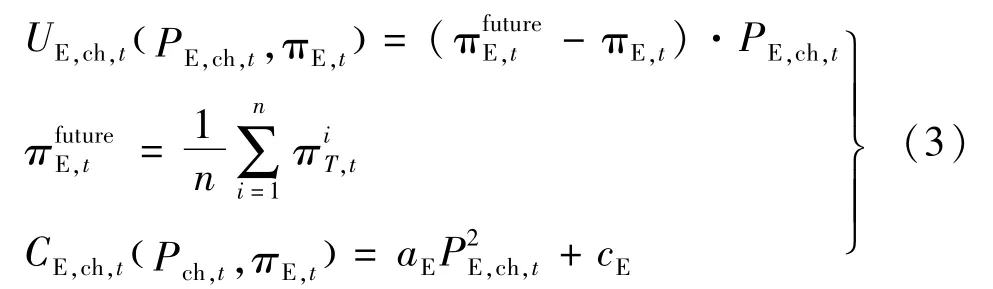
如果ESS代理通过以πE，t的实时价格输出电能来获得收益；以π表示t时刻ESS放电的收购价格，则收益必须考虑输出电能的收购价格π（πE，t＞π）。同样，在放电时也应考虑电池折旧和设备运行的成本。ESS放电时的输出函数UE，dis，t和成本函数CE，dis，t可建模：

式中：PE，dis，t为t时刻ESS的放电功率；CE，dis，t为充电状态下，电池折旧和设备运行成本；t0为调度时段的开始时间；πE，i为调度周期内i时刻的实时电价，其中i∈( t0，t)。PE，ch，i是调度周期内时刻i的充电功率。

结合ESS充放电的目标函数，可将t时刻ESS的收益函数重塑为：

式中：fE，t为t时刻ESS的收益函数；UE，t为t时刻ESS的输出函数；CE，t为t时刻ESS的成本函数。

ESS代理的主要约束条件如下：

式中：Ich，t、Idis，t分别为充、放电时维护设备所需收入；δE＞0为ESS维护设备所需的收入下限。Ddis，t、Dch，t分别为ESS的充、放电状态，用“0”“1”表示。E为ESS储能容量的上限；ESOC，t为ESS的t时刻储能容量。ESOC，t＋1为ESS的t＋1时刻储能容量；P、P分别为ESS充、放电时的功率上限；ηch和ηdis分别为充、放电状态下的电能效率。

由式（6）可知，ESS的收益是基于过去、现在和未来的电能价格，ESS的调度是通过比较当前价格来确定的。为实现ESS的经济运行，调度策略是低电价时充电、高电价时放电；为便于判断充、放电状态，以过去T小时的平均电价为标准。ESS在当前电价低于平均电价时充电，在当前电价高于平均电价时放电。这样既能保证ESS自身经济收益，又能缓解高峰负荷期的用电压力，图1所示为某省过去24 h内的实时电价曲线。

图1 某省过去24 h实时电价曲线

1.2 RG代理实时经济模型

由于RG是免费使用的，这里RG的操作成本假设为零。RG的运营收益为：

式中：fR，t为RG代理在t时刻时的运营收益；UR，t为t时刻RG的输出；PR，t为t时刻RG的实际输出；πR，t为t时刻RG的实时电价；δR为RG维护设备所需收益的下限。

1.3 CG代理实时经济模型

CG代理的运营收益为：

CG代理的约束条件如下：

式中：UC，t为t时刻CG的输出；CC，t为t时刻CG的发电成本；PC，t为t时刻CG的实际输出功率；πC，t为t时刻CG的实时电价；δC为CG的维护设备所需收益的下限。aC、bC和cC分别为CG的发电成本系数，PmaxC、PminC分别为CG的实际输出功率的上、下限。

1.4 用户代理实时经济模型

用户代理的收益定义为所有负载的收益之和［11］。用户代理（负载）的输出函数为：

式中：al、bl为用户代理的收益系数；Pl，t为负载在t时刻的功率消耗；πl，t为t时刻时用户代理（负载）的实时电价；Cl，t为t时刻时用户代理（负载）的成本。用户代理（负载）的收益为：

用户代理的约束条件为：

式中：γl为用户代理（负载）购电成本的上限；P、P分别为t时刻用户代理（负载）消耗功率的上、下限；Pl，t为t时刻用户代理（负载）消耗的功率。

1.5 孤岛微网实时经济模型

在满足可调度代理的容量限制的前提下，孤岛微网需要始终保持供需平衡并最大限度地获得收益。因此，孤岛微网的经济调度模型可表述如下：

式中：xi，t为t时刻代理i的决策变量；fi，t（xi，t）为t时刻代理i的收益；Ui，t为t时刻代理i的输出；Ci，t为t时刻代理i的成本［12］；Pi，t为t时刻代理i的功率输出；πi，t为t时刻代理i的电价；Pd，t为t时刻系统的总需求功率；Ps，t为t时刻系统的总供电功率。

2 基于ADMM的分布式解决方案

2.1 问题重构

ADMM算法能很好地解决分布式优化问题。考虑到标准ADMM算法的方程式形式，可以将孤岛微网的经济调度模型重新建模为：

式中，Pi，t为t时刻代理i的实际输出。

2.2 算法设计

根据ADMM［13］的基本原理，该模型所执行的迭代过程可以描述为：

迭代算法（15）的结束条件是：

式中：下标v、j分别为与代理i相邻的两个代理；上标k、k＋1为第k和k＋1次迭代；xi为代理i的决策变量；xi，t、x分别为t时刻代理i的决策变量及第k＋1次迭代；xij＿i，t、x分别为t时刻代理i在代理i和代理j之间的决策变量及第k＋1次迭代；xij＿j，t、x、x分别为t时刻代理j在代理i和代理j之间的决策变量及第k和k＋1次迭代；xvi＿i，t、x分别为t时刻代理i在代理v和代理i之间的决策变量及第k次迭代；u、u分别为t时刻代理i和代理j之间的输出的第k和k＋1迭代；u为t时刻代理i和代理v之间的输出的第k迭代。ρ为惩罚参数；Pij，t为相邻代理i和代理j之间的交换功率；Pvi＿i，t为相邻代理v和代理i之间的交换功率。如式（15）所示，对于功率解耦，Pij，t被复制给代理i和j，然后分别命名为Pij＿i，t和Pij＿j，t，ε是收敛阈值。在ADMM算法中，所有的代理根据交换的信息适当地调整自己的变量，直到满足收敛条件。

3 案例研究

3.1 仿真工具和参数

以系统组成为1台CGS、1台ESS、1台光伏和2台负荷组成的孤岛微网为例，分别在场景1：晴天、场景2：多云以及场景3：多雨，3个场景下进行分析。调度周期为24 h，间隔时间为1 h。ESS充、放电效率被设定为95%，最大的充、放电功率为200 kW，容量的上限限制为2 000 kW·h。各代理的系统仿真参数见表1。光伏的功率曲线如图2所示。在Matlabr2016a编译环境中，使用Yalmip优化工具对实例进行了模拟，并调用了Cplex解决方案。

表1 系统仿真参数

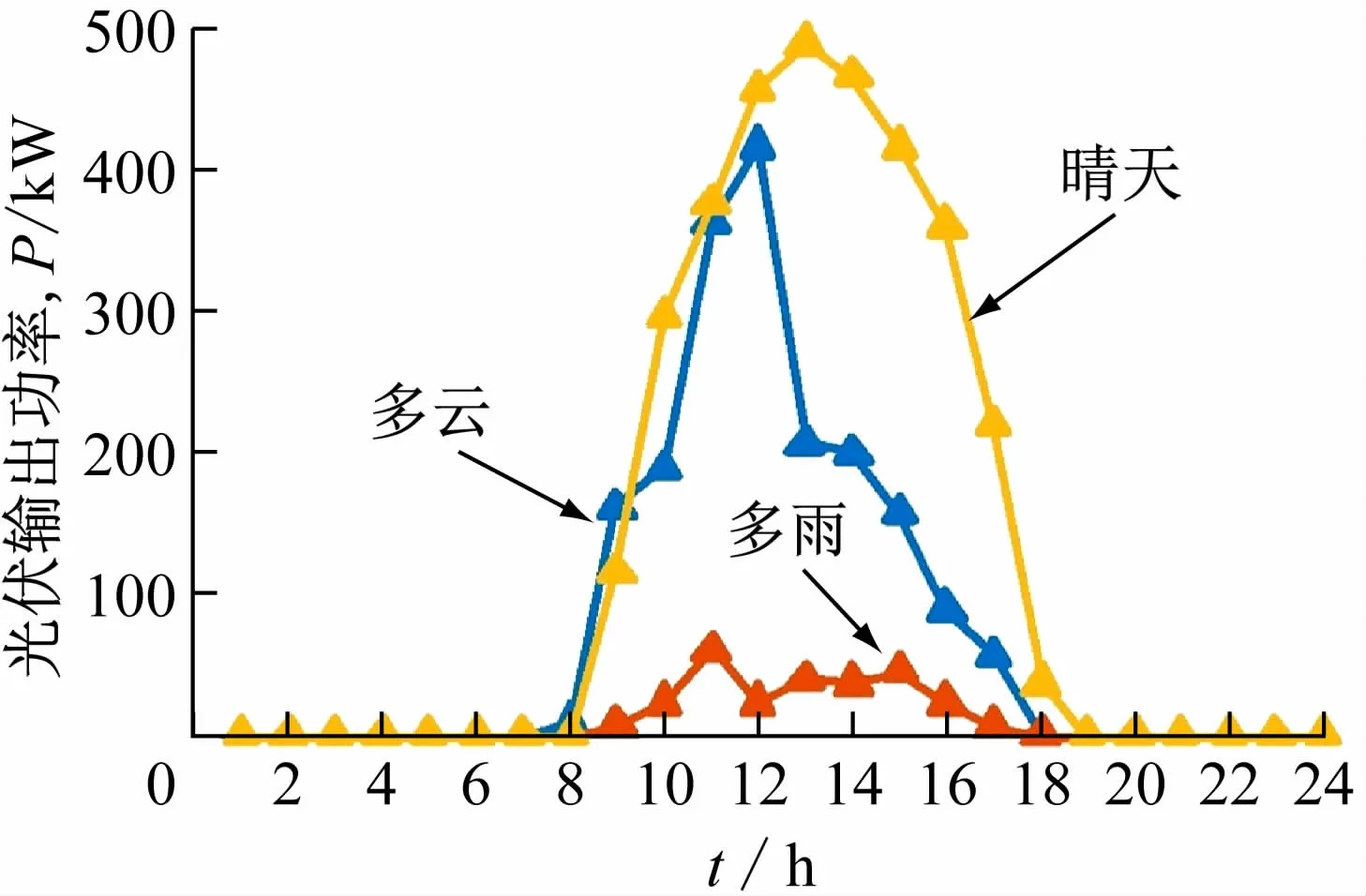
图2 3种场景下光伏输出

3.2 ESS状态判断

假设过去T小时的能源价格趋势与调度的下一个时间间隔一致。表2显示了根据图1中的实时电价获得的下一个预定周期的ESS的充、放电状态（“1”为当前状态，“0”为非当前状态）。

表2 充放电状态

3.3 最优调度结果与分析

3.3.1 调度结果与分析

图3所示为所有代理的实时总收益，图4所示为每个代理的实时收益。图5所示为优化后的每个代理的实时输出能力。

图3 所有代理的实时总收益

图4 各代理的实时收益曲线

图5 优化后各代理实时输出

由图4、5可见，当电价较低，光伏发电量较少（01：00～09：00，23：00～24：00）时，主要由CG代理供电。考虑到光伏供电的不足，虽然此时储能处于充电状态，但储能能力并不大。当负荷需求超过光伏发电量但电价昂贵（18：00～22：00、10：00～12：00）时，电力系统可以通过转售存储能源获得收益。随着光伏发电量的增加（13：00～17：00），供电量将远远高于负荷需求，为避免能源浪费，应及时对ESS充电。这样既保证了孤岛微网内的供需平衡，又达到了系统稳定运行的目的，避免了能源短缺／过剩现象造成的经济损失。

图6所示为ESS代理的优化调度结果，电价曲线和充、放电曲线表明，ESS代理在低电价下充电，在高电价下放电。由收益曲线可知，只要ESS的充、放电功率不为零，ESS代理就会实时套利。验证了本文提出的ESS收益模型的正确性。

图6 ESS代理的最优调度结果

3.3.2 3种情景下收益比较

图7～11所示为3种场景下各代理的调度结果对比。光伏发电的收益很大程度上受自身发电量的影响，因此本文没有对其进行详细的分析。

如图7所示，当光伏无输出且负荷需求较小时，3种场景下的电价基本相同。总的来说，由于光伏输出不能满足负载的需求，电力短缺需要其他发电代理（CG、ESS）进行补偿，雨天电价与其他两种场景相比相对昂贵。用户代理在这3个场景下的收益如图8所示。

图8 3种场景下用户端收益

在雨天，由于功耗主要由CG和ESS提供，这将导致用户代理的效益最低。在晴天，光伏输出优先满足负荷需求。考虑到大多数国家的政策和环境问题，光伏发电成本被认为是零。在这种情况下，消费者可通过以相对较低的电力成本消耗更多的电力来创造更多的利益。晚上20：00左右，3个场景下的电源都只能由ESS和CG进行补偿。但在雨天或多云，由于ESS剩余可用容量较小，负荷需求主要由CG提供。因此，在这两个场景下，20：00左右的用户代理的收益就更少了。

图9显示了3种场景下CG代理的收益比较。光伏作为一种不可调度的能源，优先为负载提供能量。当光伏输出不能满足负荷用电时，采用CG代理来维持孤岛微网内的供需平衡。在阳光明媚的日子里，CG代理的收益是最低的。相反，CG代理在雨天的收益最高。

图9 3种场景下CG代理的收益

图10的收益曲线表明，充电时的ESS相当于负载，放电时相当于发电机。10：00～12：00，由于ESS处于放电状态，雨天收益最大。13：00～17：00期间，ESS处于充电状态，晴天收益最大。尽管ESS在18：00～20：00期间放电，结合图11中的ESS剩余容量曲线，场景2和场景3下的ESS效益由于剩余容量不足而非常低。

图10 3种场景下ESS代理的收益

图11 3种场景下ESS代理的剩余容量

4 结 语

针对孤岛微网实时经济调度问题，给出了一种新的优化模型。该模型具有时间耦合特性的ESS可以解决其实时性问题。模型使用ADMM来实现系统收益的最大化。在实施过程中，各代理只需与相邻代理交换期望电价和交易功率，因此通信负担非常轻。仿真结果证明了该优化策略是行之有效的。应考虑两个方面的改进。需要提高获得ESS充、放电状态的准确性；需要在结构更复杂的孤岛微网上测试所提模型的有效性。