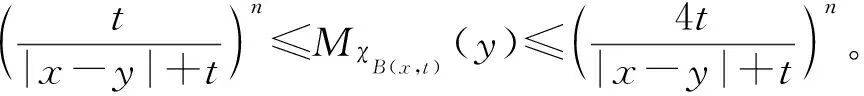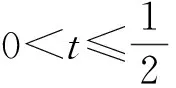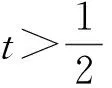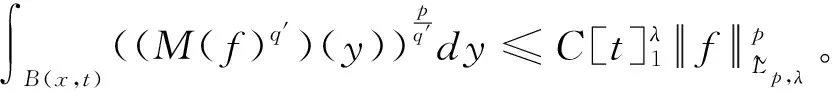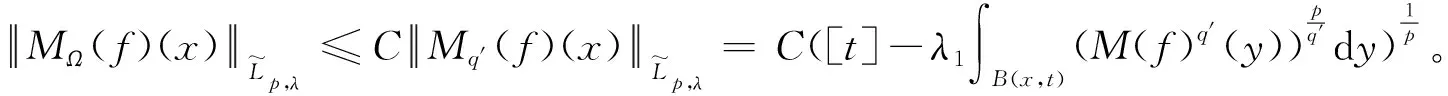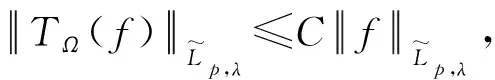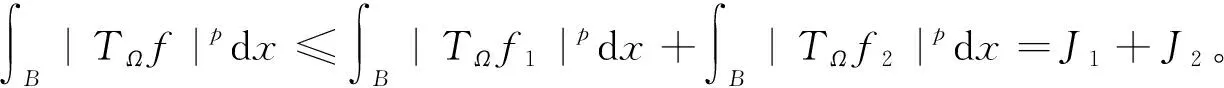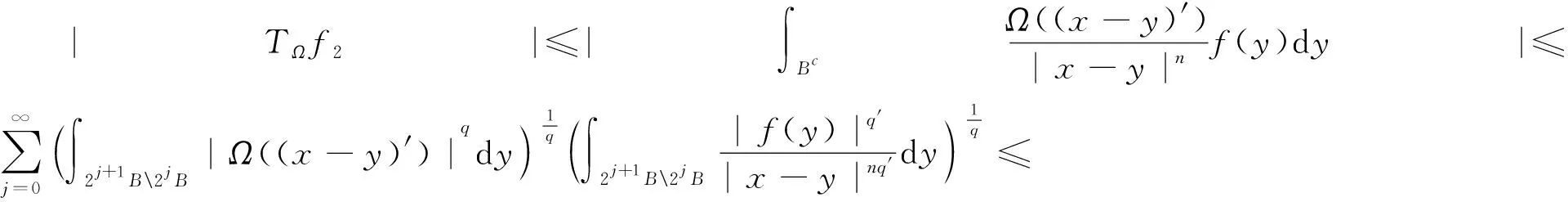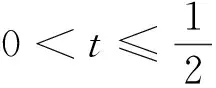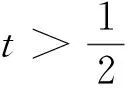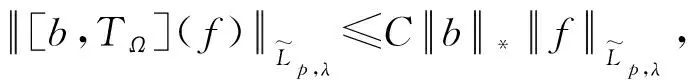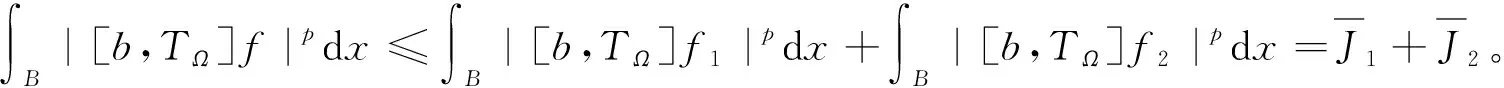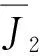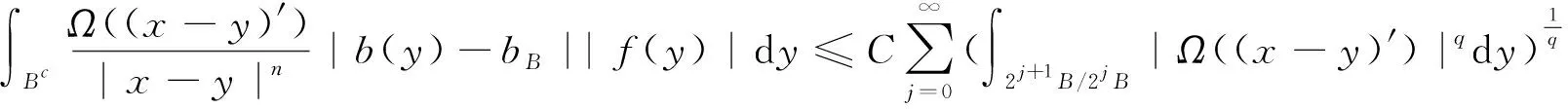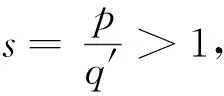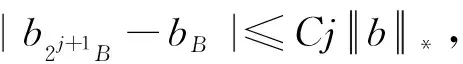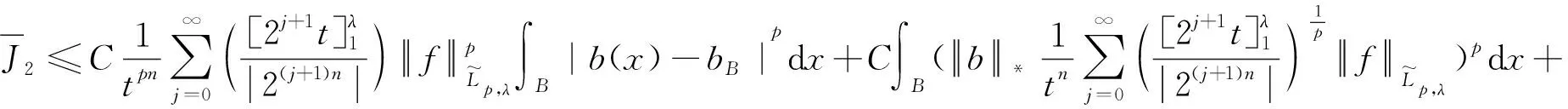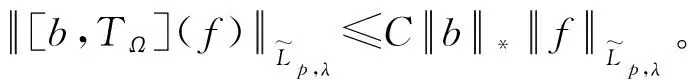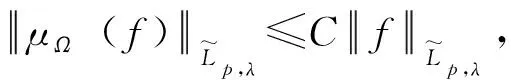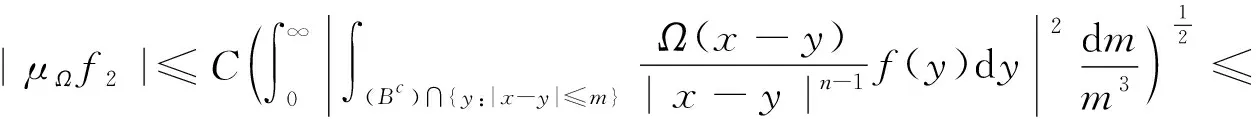粗糙核算子在修正Morrey空间中的有界性
2022-03-22 11:18:40张霖
厦门理工学院学报 2022年1期
张 霖
(湖北师范大学数学与统计学院,湖北 黄石 435002)
当x∈Rn及t>0时,令B(x,t)为中心在x、半径为t的一开球。
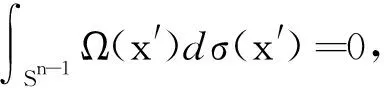
令b是Rn中一局部可积函数,交换子[b,TΩ]定义为[b,TΩ]f(x)=b(x)TΩf(x)-TΩ(bf)(x)。高维的Marcinkiewicz积分算子μΩ定义为
1938年,Morrey为研究椭圆型偏微分方程解的存在性和可微性,引入Morrey空间Lp,λ(Rn)[1]。后来,Morrey空间被应用于研究N-S方程[2-3]、薛定谔方程[4]和带有不连续系数椭圆方程[5]。鉴于Morrey空间的重要性,人们开始研究广义Morrey空间[6]。2011年,文献[7]提出了修正的Morrey空间,并研究了分数次极大算子和带有Riesz势算子在修正的Morrey空间有界性。这里修正的Morrey空间是包含于Morrey空间与勒贝格空间之交。
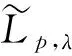
1 记号和预备知识
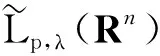
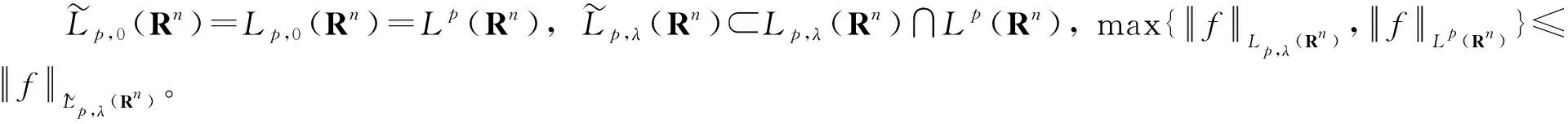
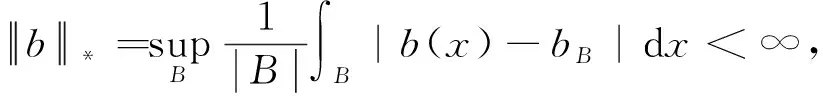
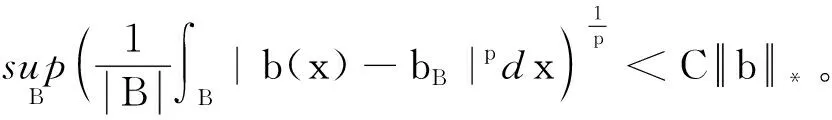
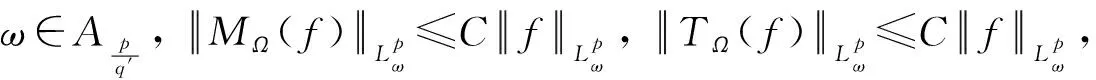
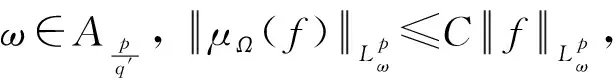
2 主要结论
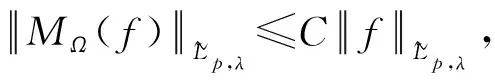
证明当q′ 现在考察当p=q′ 时的情形。取一球B=B(x,t)⊆Rn及作f=f1+f2(f1=fχB)分解, 得到 利用定理2,有 (1) 由此得到, (2) 由式(1)和式(2),定理4得证。 为了得到J2的估计,运用Hölder’s不等式,得到 (3) 当p=q′时,分为2种情况。 综上,只要t>0,就有 (4) 当p>q′时,有 (5) 利用Hölder’s不等式, 有 证明取一球B=B(x,t)⊆Rn及作如下分解f=f1+f2(f1=fχB),有 由定理3,得到 (6) 为了估计K2,由不等式(3)和式(6), 有 因此,当1 (7) 结合不等式(6)~(7),得到定理7。