基于节点高程差的DMA 边界划分研究
谷洋
(浙江大学建筑工程学院,杭州 310058)
0 引言
随着智慧水务城市建设的逐渐推进,以被动检漏为主的传统技术手段和以经验为主的管理模式已经无法适应日趋庞大和复杂的供水管网。作为管网漏损控制的最小管理单元,独立计量区域(District Metered Areas,DMAs)逐渐成为了漏损主动管理最有效的途径之一,通过关闭管道阀门将部分管段截断,把供水管网划分成若干个相对独立的区域,并在每个区域入口和出口管道上加装流量计,实现对各分区流量的实时监测,能及时发现供水管网漏损点的位置,并修复止损,提升管网的精细化和网格化管理水平[1]。
DMA 分区管理的基础在于分区边界管段的确定,根据目前的研究,主要有人工经验分区和算法自动分区两种方法。其中,人工经验分区是指根据管理者的主观经验,综合考虑行政边界、河流道路、用户数量等要素划定DMA 边界,并利用水力模型检验分区效果。但实践表明对于结构复杂的大型环状管网,使用人工经验分区存在诸多局限性。一来管网规模的增大会增加分区校验的难度和时间;二来经验法没有充分考虑到供水管网的水力运行条件,难以确定边界阀门的最佳安装位置。因此,很多学者进行了算法自动分区的研究。算法分区方法通常以图论为基础,通过将复杂的管网结构等效成拓扑图模型,再借助算法完成DMA分区。
Sempewo[2]等以节点需水量和管段长度作为节点权重,以管径作为边的权重构建管网的加权拓扑图,利用METIS 图划分软件进行分区,使得各DMA 间边界管段数量最小化。Di Nardo[3]等先提出了一种基于图论和遗传算法的DMA 分区方法,该方法指出节点和管段的最佳权重组合是需水量和耗散功率,并以耗散功率最小化为优化目标确定了阀门和水表的安装位置;之后又提出使用谱聚类算法进行分区[4],使用平均割和规范割两种划分方式,寻找最佳分区方案。Herrera[5]等先是以需水量和管径作为节点和管段的权重构建相似矩阵,但运算效率较低。为了改进这一问题,又提出了一种多智能体自适应谱聚类算法[6],该方法以水源为起始点,迭代搜索与之相似的节点形成DMA,但受水源数量的限制,计算得到的分区数量不能多于水源点数量。Diao[7]等提出了一种基于拓扑结构演化的DMA 分区方法,该方法依据复杂系统分解原理研究管网的社区结构(即DMA),并使用模块度指标量化分区效果,使得社区内部连接边密集,社区之间连接边较少。
文中提出了一种基于节点高程差的供水管网DMA 边界划分方法,引入管网节点的高程差改进相似矩阵并使用谱聚类算法求解。通过选定合适的分区数量,使得改进结果在不影响分区规模均衡性的基础上,改善同一分区内节点高程的均衡性。
1 供水管网DMA 分区边界模型的建立与求解
1.1 基于节点高程差的相似矩阵的构造
在供水管网图模型中,选取合适的管网属性定义节点相似度(即管段权值),进而构建相似矩阵是求解DMA 划分边界最基础、也是最关键的一步。
传统谱聚类算法通常用高斯核函数构造相似矩阵,但在实际供水管网DMA 分区中,还要考虑地理条件、分区规模、供水安全性等因素对分区的影响。文中主要考虑地形高程这一因素,将地形高程的变化等效成管网标高的变化,因为在供水管网布置中,通常是顺着地形高程的变化敷设供水管道地形的高程很大程度上决定了管网节点的高程[8]。而节点间的高程变化又直接影响到管网供水压力的分布,尤其是针对山地或丘陵地区的供水管网,节点高程差较大容易造成供水压力分布不均匀,形成局部的高低压区域。高地势区的用户水压通常难以保证,而低地势区的用户水压会产生冗余,存在爆管和漏损的风险。同时,分区地势跨度较大还会增加管道埋设的难度和施工成本,为日常的运营维护带来困难。因此,在分区时应尽量保证同一个DMA 内节点高程的一致性。
文中利用管网节点间的高程差ΔHij来构造相似矩阵,相似矩阵表示为:
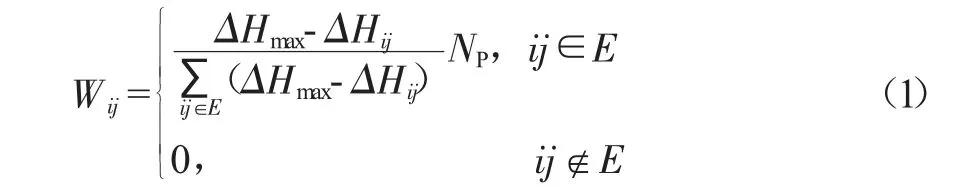
式中,ΔHmax为管网所有节点间高程差的最大值,m;ΔHij为节点i、j 间的高程差,m;NP为管网的管段数。
为检验算法的改进效果,文中选用一种基于局部标准差的自适应谱聚类算法[9]作为改进前的算法进行对比,该算法在传统谱聚类算法上进行改进,为每个样本点i 设定一个局部标准差尺度参数σstd,i,避免了人为设定全局尺度参数σ 对算法本身的影响,改进前算法的相似矩阵表示为:
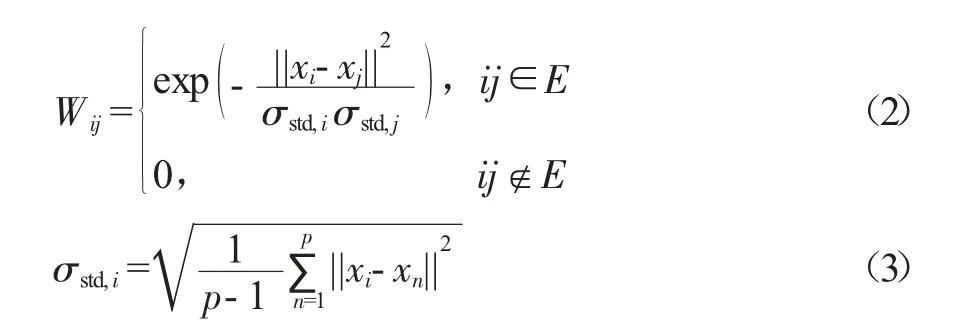
式中,||xi-xn||表示样本点i、n 间的欧式距离;p 为预先设定的样本点i 的计算近邻数;σstd,i反映了样本点i 与其前p个近邻点间距离的标准差。
1.2 DMA 分区数量的选择
使用谱聚类算法进行DMA 分区时,分区数量k的选择是很关键的一步,它直接影响着分区规模的大小、经济可行性和水力可靠性。传统方法依据用户数、用户需水量和管线长度等因素拟定分区数量,但主观性较强,而且对于大型复杂管网耗时耗力,直接拟定的分区数量很难满足最佳水力运行条件。文中选用边界管段数量、聚类有效性指标STDI[10,11]和模块度Q 三个指标评估DMA 的边界划分方案,初步选择合适的分区数量。其中,聚类有效性指标STDI 定义为:
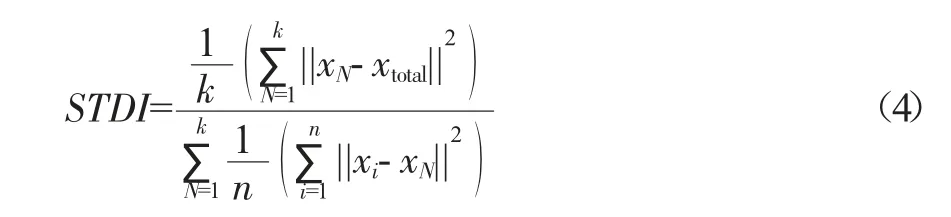
式中,xtotal为所有节点的质心;xN为第N个分区中所有节点的质心;xi为第N个分区中的第i个节点;n为第N个分区的节点数量;k 为分区数量。模块度Q 定义为:

式中,m 为管网管段数;Wij为管网图模型的相似矩阵;di、dj为节点i、j 的度;δ 为克罗内克函数,用于判断节点i 和j 是否在同一个DMA 内,若节点i 和j 同属于一个DMA,则δij=1,否则δij=0。
边界管段的数量越少,表明需要安装的阀门和流量计的数量越少,经济成本越低;聚类有效性指标STDI 可以有效表征子图内部的紧密性和子图间的分离性,STDI 的值越大,表明聚类的效果越好;模块度Q来源于社区发现算法,用来定量描述社区划分的模块性水平,Q 的最大值是1,Q 值越接近1,表明DMA 划分效果越好。
1.3 DMA 边界模型的求解
文中使用谱聚类算法求解DMA 边界模型,它是一种基于谱图划分理论的聚类算法,基本思想是以样本对象为顶点V,以样本间相似度对连接边E 赋权重w,构造无向有权图G=(V,E),进而将聚类问题转化为图的最优划分问题[12]。求解时需要运用维度规约的思想对问题进行连续放松来减少约束,将其转化为相似矩阵或Laplacian 矩阵的谱分解问题[13],使划分得到的子图内部相似度最大,子图间的相似度最小。图1 为使用谱聚类算法求解DMA 边界模型的基本流程。
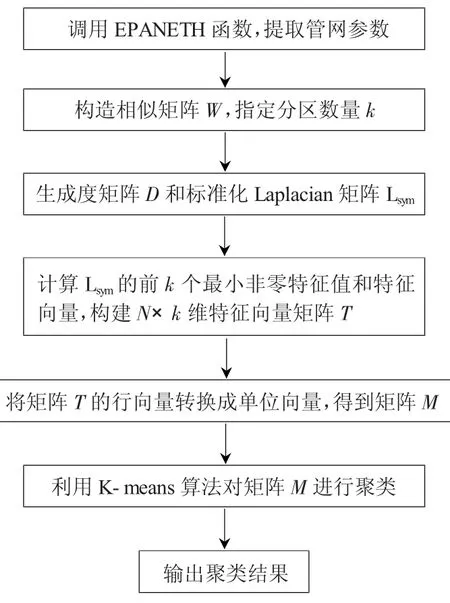
图1 DMA 边界模型的求解流程
这里分别使用基于局部标准差和节点高程差的自适应谱聚类算法作为改进前后的算法对供水管网节点进行聚类,两种算法的唯一区别在于相似矩阵的构造。对于改进后的谱聚类算法,只需要导入管网模型外部文件(.inp),便可利用EPANETH 功能函数提取节点高程等参数,直接生成相似矩阵;但对于改进前的算法,还需要导入管网地图文件(.map)中的节点坐标,并人为给定计算近邻数p,才能得到相似矩阵。
2 算例验证
2.1 算例管网介绍
采用文献[14]中的Modena 管网,所有数据均沿用原文。该管网有268个需水节点,4个水源节点,317根管段,管网总长约72km,总需水量为406.94L/s,需水节点标高的最大值为30.39m,最小值为41.83m,管网最小服务水压为14m。
2.2 DMA 分区数量的初选
预设管网的分区数量范围为2~15个,取改进前算法的计算近邻数p=2,并依次使用改进前后的谱聚类算法求解得到不同的聚类方案,最后计算不同分区数量对应的边界管段数、聚类有效性指标STDI 和模块度Q 进行对比评估。图2、图3 分别为不同分区数量下3个指标的比较。
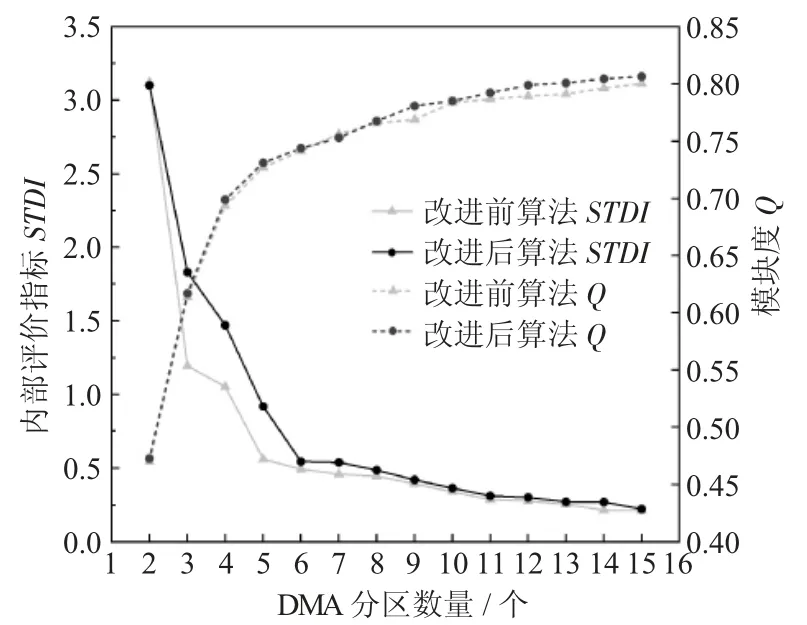
图3 分区聚类有效性指标和模块度的比较
从图2 可以看出,随着分区数量的增加,边界管段的数量逐渐增多,意味着安装阀门和流量计的数量和费用会随之增加。对比算法改进前后的指标值可以发现,当分区数量大于3个时,引入节点高程差改进后的边界管段数量较改进前均有增加,原因在于Modena 管网标高分布呈单向层次(即西高东低),在构造相似矩阵时,沿管网等高线方向的管段权值较大,这样聚类就会使得分区层次相对明显,但产生的边界长度也会随之增加,需要“截断”更多的管段。因此在确定分区数量时,应优先选择边界管段数量较少,且算法改进对其影响较小时对应的分区数量。

图2 分区边界管段数量的比较
从图3 可以看出,随着分区数量的增加,STDI 逐渐减小,Q 逐渐增大,且当分区数量大于6个时,指标值的变化速度减缓,表明聚类效果不再有明显改变。对比算法改进前后的指标值可以发现,引入节点高程差使得STDI 和Q 值均有所增加,且当分区数量k=3、4、5时,STDI 值变化较大,表明引入节点高程差使得分区内部联系更加紧密,体现出改进后算法的明显优势;相比之下,Q 对于算法改进的敏感度不强。因此在确定分区数量时,应优先选择STDI 和Q 值均较大时对应的分区数量,还应兼顾算法改进对指标变化的影响。
综合考虑以上3个评价指标,初选DMA 分区数量为3个或4个,得到对应的改进前后分区示意图如图4、图5 所示。
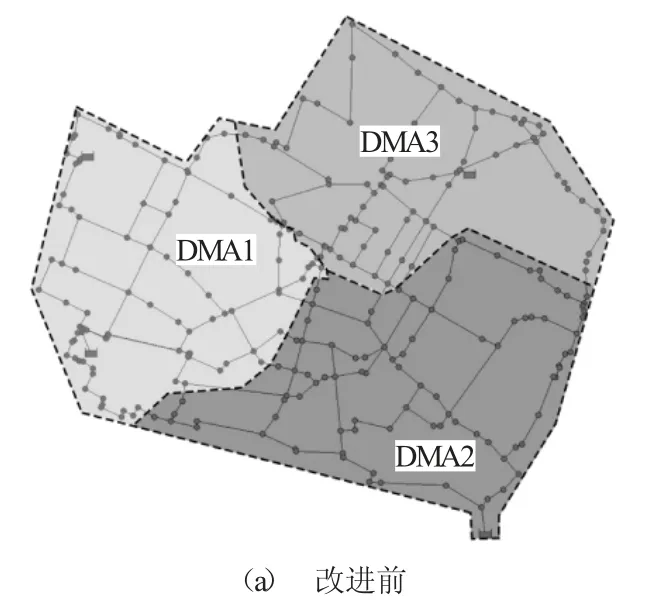

图4 分区数量k=3 时的Modena 管网DMA 边界划分结果
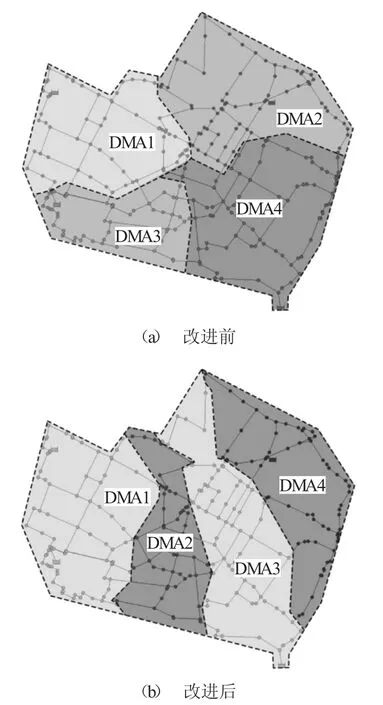
图5 分区数量k=4 时的Modena 管网DMA 边界划分结果
2.3 DMA 边界划分结果分析
2.3.1 分区高程均衡性评价
为了验证改进算法在DMA 边界划分中的优化效果,文中选用分区节点高程变差系数Cv,H衡量各DMA内高程的均匀性,指标定义为:
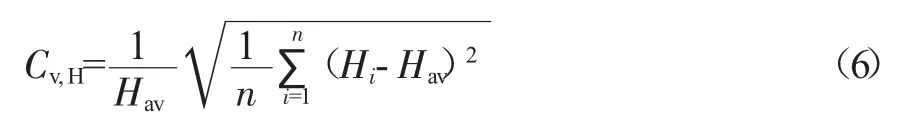
式中,Hav为分区内节点的平均高程,m;Hi为分区内节点i 的高程,m;n 为分区内的节点数。Cv,H越小,表明分区内节点的高程值越接近,算法改进的效果越明显。
表1、表2 分别为分区数量为3个和4个时,各分区在算法改进前后的节点高程变差系数的比较。通过计算得到,改进后DMA 分区内高程均衡性分别提高了16.06%和23.39%,表明引入节点高程差构造相似矩阵对改善分区高程均匀性、克服地势对DMA 分区的影响有较大意义,且当分区数量为4个时,高程改进效果更明显。

表1 分区数量k=3 时的各分区节点高程变差系数的比较
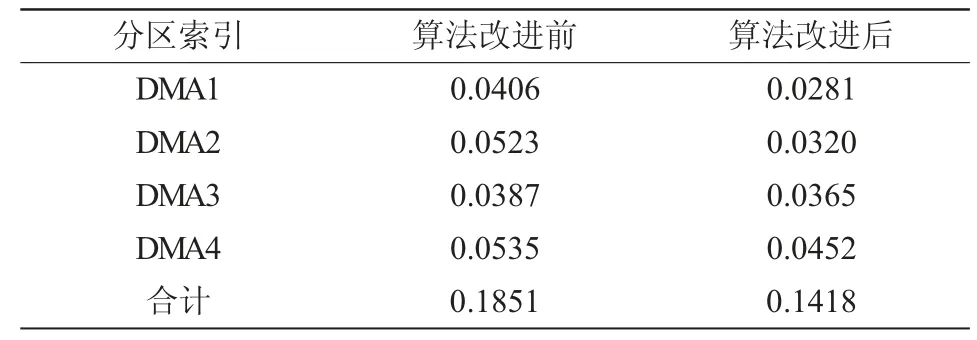
表2 分区数量k=4 时的各分区节点高程变差系数的比较
2.3.2 分区规模均衡性评价
在DMA 分区管理中,分区规模的大小会直接影响管理的难度和效果,规模相差较大会提高管网漏损和爆管的识别定位难度,增加不必要的经济成本,因此文中另选用分区规模均匀度FS对划分方案进行核算,确保算法在改善分区高程均衡性的同时,不破坏分区规模的均衡性。指标定义为:

式中,Wd,i为第i个分区的总需水量,L/s;Wd,av为所有分区的平均需水量,L/s;k 为分区数量。从定义可以看出,FS是用需水量来表征分区规模差异性的,即FS越小,表明各分区需水量差异越小,分区规模越均衡。
表3、表4 分别为分区数量为3个和4个时,各分区在算法改进前后的需水量和节点数量的比较。通过计算得到,当k=4 时,改进前后的FS分别为25.63 和22.49,引入节点高程差使得分区规模均衡性提高了12.25%;但当k=3 时,改进前后的FS分别为11.92 和35.78,指标增加了近2 倍,显然,节点高程差的引入破坏了分区规模均衡性,不利于DMA 的计量管理。

表3 分区数量k=3 时的各分区需水量和节点数量的比较
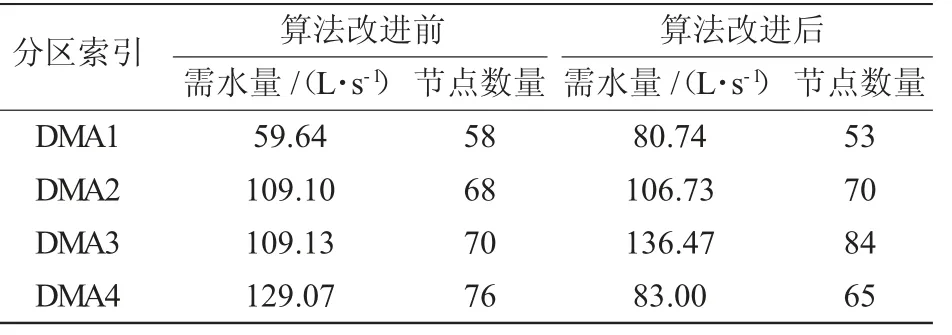
表4 分区数量k=4 时的各分区需水量和节点数量的比较
综上所述,将Modena 管网分为4个DMA 更为合理,既实现了较好的聚类效果,节约边界设备的布置成本,又可以在不影响分区规模的基础上提高分区高程的均匀性,降低地势跨度对DMA 分区的影响,从而间接改善供水压力分布,维持管网的供水安全性。
3 结语
文中将供水管网等效成节点和管段的无向有权图,提出了一种基于节点高程差的DMA 边界划分方法。该方法引入管网节点高程差改进相似矩阵,并使用谱聚类算法求解,尽可能保证同一分区内节点高程分布更加均匀。同时从边界管段数量、聚类有效性指标和模块度3个指标量化聚类效果,确定合适的分区数量。文中使用Modena 实例管网验证了分区方法的有效性,可以为水务公司,尤其是山地或丘陵地区的水司提供DMA 分区方法的参考。

