四轴平台奇异点机理分析
同昭豫 江泽
摘?要:针对平台系统需要满足载体做大机动飞行的背景下,因奇异点的存在导致回路稳定性恶化的问题,对四轴平台的运动机理进行了研究分析。对于平台式惯导系统而言,当四轴平台外框轴旋转±90°时,随动框轴与内框轴由原本的共线关系变成了正交关系,随动框的伺服随动作用便趋近于0,我们一般称之为奇异点。为此,本文在理论上推导了奇异点处无法工作的原理,并证明了奇异点的唯一性,为对四轴平台稳定性更进一步的研究提供了强有力的保障。
关键词:惯性平台;奇异点;四轴平台
在现代导航应用中,无论是远程导弹还是飞机火箭,精度已经成为衡量其效能的首要因素。随着多种导航系统的发展与应用,惯性导航以其实时性、连续性和自主性等优点,一直被广泛应用[1-3]。惯导系统又分为惯性平台系统和捷联惯导系统,平台相较于捷联系统的优点在于通过框架隔离载体的角运动,使平台台体相对惯性空间始终保持稳定,为导航解算用的加速度计提供一个良好的工作环境[4-6]。
对于四轴平台而言,现有文献认为当其外框轴旋转±90°时,会出现随动伺服回路飞车现象,使得平台失去全方位机动能力。为此,近几年国内针对平台系统的控制策略做了许多研究。文献[7]针对平台系统的飞转做了详细研究,分析其产生原理并提出了算法。文献[8]提出了一种对随动框架控制的方法,当四轴平台的外框轴处于奇异点时通过翻转控制方法,使得四轴平台保持其正常功能。文献[9]提出在奇异点断开回路或者对除法器限幅这两种方案,保障四轴平台在奇异点稳定工作。这些研究虽然提出了控制策略,保障了平台系统全姿态能力的机动性,但并未从机理上对奇异点的原理进行分析。为此,本文针对四轴平台的奇异点机理进行了分析,证明了奇异点的存在性以及奇异点的唯一性。
1 四轴平台坐标系定义及动态模型
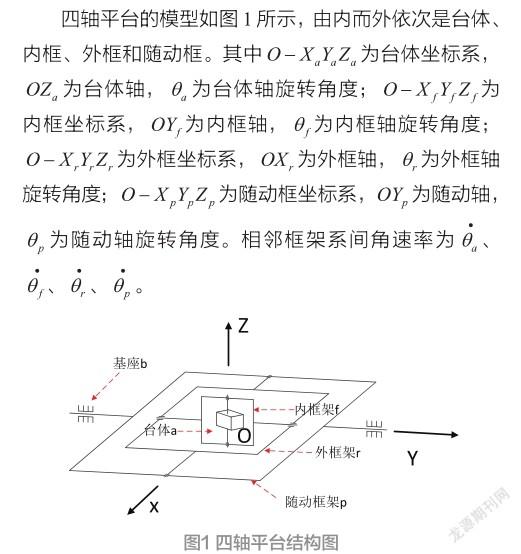
在机体飞行过程中,机体角速度的变化是整个系统的输入,通过框架轴物理关系逐层传递到台体坐标系,并且由刚体运动学中“绝对运动=牵连运动+相对运动”作为理论支撑,根据上述定义,由基座坐标系b到台体坐标系a的传递关系可定义如下。

2 奇异点机理分析
四轴平台的随动框架对内框轴有伺服控制作用,通过旋转随动框轴来平衡内框轴的转动角速度,保障台体轴、內框轴和外框轴始终保持正交状态。我们一般认为其奇异点为外框轴处于±90°时,此时随动框轴从Y轴转到Z轴,与仍然处在Y轴的内框轴正交,如图3所示,与此同时随动框轴就失去了对内框轴的伺服控制能力。

2.1 奇异点存在性
我们针对以往的实验现象推导其理论机理,研究四轴平台奇异点存在性原理。由于四轴平台的内框轴始终处于零位,因此我们以内框架角速度为平衡点,建立从台体到内框的迭代式以及从基座到内框的迭代式,其中基座到内框的迭代式由式(1)(2)(3)可推出:




3 结论
本文利用惯性平台系统惯性空间中稳定的原理,通过对四轴平台的机理分析,论证了其奇异点无法工作的原理,同时证明了四轴平台的奇异点有且只有一个,为四轴平台的研究分析提供了强有力的保障。
参考文献
[1] 秦永元编著.惯性导航(第2版)[M].北京:科学出版社.2014.
[2] 高桂杰,张艳霞,夏刚,魏宗康.四轴平台随动系统的模型分析与设计[J].导航与控制,2014,13(4):21-25,31.
[3] 李海霞,高钟毓,张嵘,韩丰田.四轴陀螺稳定平台的变结构分区控制[J].清华大学学报(自然科学版),2010,50(7):1023-1028.
[4] 魏宗康,夏刚,高桂杰,徐强.四轴平台伺服系统建模研究[J].中国惯性技术学报,2002(5):7-11,20.
[5] Strategic inertial navigation systems - high-accuracy inertially stabilized platforms for hostile environments[J]. IEEE Control Systems, 2008, 28(1):65-85.
[6] James A. Van Allen. Basic principles of celestial navigation[J]. American Journal of Physics,2004,72(11):67-72.
[7] 张娜,赵军虎,余贞宇.一种基于三框架四轴惯性平台的飞转判断算法[J].导弹与航天运载技术,2020(01):67-71.
[8] 赵军虎,洪娟,李渤弘.四轴惯性平台随动框架控制策略研究[J].导航与控制,2017,16(4):32-37.
[9] 康尧磊,王汀,朱志刚.四轴平台外框架角±90°时运动特性仿真分析[J].导航与控制,2009,8(2):1-8.
3349500589210

