水锤效应——2021年亚洲物理竞赛理论第一题

陈仓佚 吴 波 宋 峰

(1.成都天府第七中学 610218；2.南开大学物理科学学院 300071)

本题研究管道中的流体因为压力波引起的压强变化，主要处理由于快速和慢速关闭管道中阀门导致的水锤效应。

为简化计算，要求只考虑非黏性流体的一维流动。所有管道及阀门都看成是刚性的，但流体是可压缩的。体积为V0的流体单元在压强P0作用下处于平衡状态，如果压强改变量为ΔP,则体积改变量ΔV与ΔP成正比，表示为

比例系数B表示液体的体积模量。对于水，密度为ρ0=1.0×103kg/m3，体积模量为B=2.2 GPa。

A部分：压强变化和压强波传播

在长度为L均匀圆柱形管道中，水沿着x轴正方向稳定流动，水平方向速度为v0，密度为ρ0，压强为P0。如图1所示，管道与储液器相连，离水面深度为h，储液器与大气相通，大气压强记为Pa。

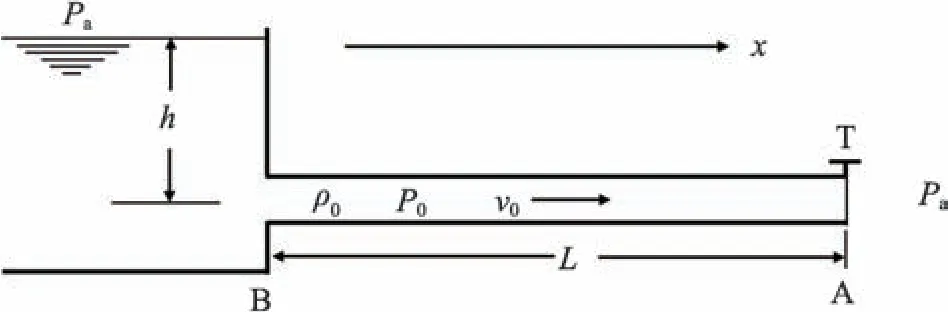
图1 均匀管内的稳定液体流动

假设位于管道末端的流量控制阀T瞬间关闭，阀门附近将要流出管道的液体会承受压强的变化ΔPs≡P1-P0和速度的变化Δv=v1-v0(v1≤0)。这会引起压强变化ΔPs通过纵波的形式以传播速度c沿x轴负方向传播。

问题A.1压强变化ΔPs与速度的改变量Δv的关系可表示为ΔPs=αρ0cΔv。压强波的传播速度为。试求出α，β和γ。(1.6分)

问题A.2 在水流速度v0=4.0 m/s，v1=0 条件下，计算压强波的速度c和ΔPs的大小。(0.6分)

B部分：流量控制阀模型

图2 为液体流经流量控制阀T 时的物理模型。控制阀门靠近管道的A 端，长度为ΔL，内半径为R。阀门锥形出口的半径为r，与大气相通，大气压强为Pa。重力对射流的影响可以忽略。

液体被认为是不可压缩的，阀门入口处的稳定流动的液体速度为vin，压强为Pin，密度为ρ0。图2中，画出的流线及其法线，只是为了帮助看清流动图样。

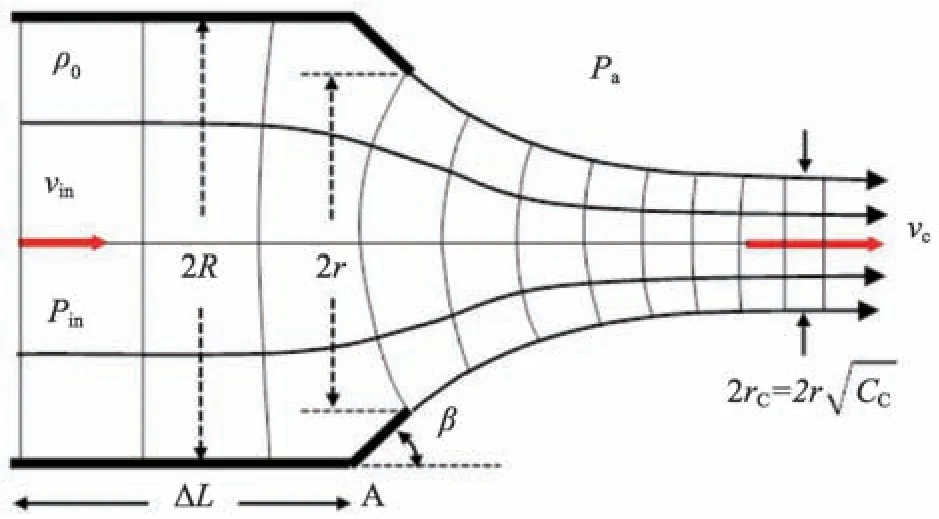
图2 阀门尺寸和喷射口的收缩示意图

流体离开阀门进入大气后，流体的横截面将收缩直到达到最小值，此时流线将再次平行。在这个最小值处，流体速度为vC，流体横截面半径为。CC被称为收缩系数，由阀门的内半径与锥形孔洞半径的比值r/R以及锥角大小β决定，见表1。

表1 喷射口孔洞的收缩系数

问题B.1 求出当阀门入口处流线平行时的ΔPin=Pin-Pa，用ρ0，vin,r，R,和CC表示。(1.0分)

本题目C和D部分，对于图1所示的储液器-管道系统，有如下假设条件：

(1)传播速度c和液体密度ρ0是与流速无关的常数。环境大气压Pa和重力加速度g为常数。

(2)最初阀门完全打开，管道中的流体稳定，其压强为P0，流速为v0。

(3)图1 和图2 所示的管道长度为L，半径为R。阀门T 是一个半径r可变的圆形开口，锥角β=90°。阀门的长度ΔL可忽略不计，阀门入口紧挨管道的A端。重力对射流的影响可以忽略。

(4)储液器中的液体是准静态的，因此其靠近管道入口B的压力Ph保持恒定。管道中的流体压力变化可以忽略，因此整个管道中的液体流动是一维的。

C 部分：流量控制阀快速关闭引起的水锤效应

对于图1中所示的储液器-管道系统，当管道中的液体流动被完全或部分关闭的阀门阻塞时，将会产生向上游传播的压强波。压强波在管道末端碰到储液器后将向阀门反射，并在阀门端再次反射形成另一个压强波。以上过程不断重复，从而导致阀门附近的液体产生一系列的压强大小的突变，这个现象称为水锤。

问题C.1参考图1和图2，当阀门T完全打开(r=R)时，求出管道内稳定流体的压强P0和速度v0。用ρ0，g，h和Pa表示。(0.6分)

问题C.2 考虑与问题C.1 中具有相同压强P0和速度v0的稳定流体。在t=0 时，阀门立即关闭(r=0)。压强波以传播速度c朝着储液器移动。管道B端的压强为Ph=P0+ρ0gh，令τ=2L/c。当时间t非常接近τ/2和τ时，管道内流体压强P(t)和流速v(t)是多少？(1.2分)

D 部分：流量控制阀缓慢关闭引起的水击效应

再次考虑与问题C.1中具有相同压强P0和速度v0的稳定流体。缓慢关闭阀门，并采用有限步方法模拟关闭过程。

从时间t=0 开始，阀门半径r的瞬时缩减量按时间间隔τ=2L/c依次给出(表2)。每次半径减小后，阀门区域内的流动可被近似为立即稳定，与B部分所示情况相同。此时阀门处的压强和速度与管道中其他流体的不同。

表2给出阀门每个关闭步骤n的持续时间和阀门开口的半径rn，并且给出阀门处相应时刻的流体压强Pn和流动速度vn。

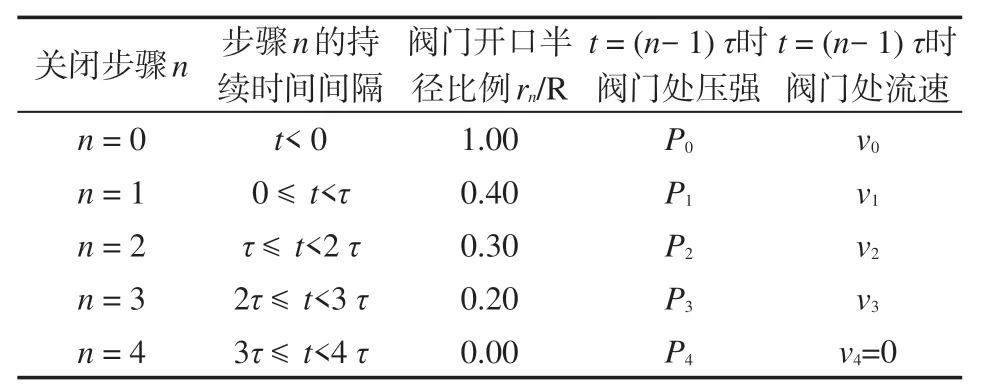
表2 阀门关闭步骤

液体密度ρ0和压强波传播速度c均看作常数。步骤n=0、1、2、3、4，压强改变量为ΔPn=Pn-P0，速度改变量为Δvn=vn-v0，Ph与P0近似相等(Ph=P0)。

问题D.1 求出ΔPn/(ρ0c)的表达式，用ΔPn-1/(ρ0c),vn-1和vn，该表达式应适用于表2 中所有n>0 的关闭步骤。对于n=1、2、3，在vn-1和ΔPn-1/(ρ0c)都已知的情况下，求出能够计算vn的表达式。(3分)

问题D.2 根据问题D.1 的结果，取水流的速度v0=4.0 m/s，绘制出所有的ΔP-ρ0cv图。对于所有的关闭步骤n=1、2、3、4，给出所画直线和曲线的交点坐标，应给出ρ0cvn和ΔPn的值，同时在图中标出每个交点坐标(ρ0cvn,ΔPn)所对应的n的值。从图中估算n=1、2、3、4时ρ0cvn和ΔPn的值(均以MPa为单位)。

赛题背景

流体沿压力管道(如输油、输水等管道)流动时，若突然关闭或开启阀门、或者水泵突然停机或启动，流体流动速度将发生突然变化；同时由于流体惯性和可压缩性，流体压强将产生剧烈的周期性变化，此现象被称为水击或水锤(Water-Hammer Effect)。发生水击现象时，管道内压强波动可能达到额定工作压强的几十倍甚至几百倍，管壁及管道上的设备及附件将承受很大的高频交变压力，产生剧烈振动并发出犹如锤击的声音。该交变压力可能造成阀门破坏、管件接头破裂、断开，甚至管道炸裂等重大事故。因此压力管道中水击现象的危害及防治研究是一项重要的工业工程问题①-②。

本题即以水击效应为背景，讨论压力管道阀门关闭时流体压强和流速的变化。