基于神经网络和模糊逻辑的BDFM直接转矩控制
乔维德
(无锡开放大学 科研与质量控制处,江苏 无锡 214011)
0 引言
无刷双馈电机(Brushless Doubly-Fed Machine,简称BDFM)结构简单坚固、运行可靠、易于维护,是一种适用于交流变频调速运行和变速恒频运行的新型交流电机,在变速驱动、风力水力发电系统等控制领域有着良好应用与发展前景.无刷双馈电机系统控制主要采用矢量控制、直接转矩控制两种控制策略.其中,直接转矩控制相对矢量控制而言,转矩响应速度较快,电机参数鲁棒性较强.
许多学者都开展了无刷双馈电机直接转矩控制策略的研究.李冰等设计了一种无刷双馈电机空间矢量调制的直接转矩控制方案,由转矩、磁链PI控制器取代传统的滞环比较器, 对转矩误差、磁链误差加以补偿[1].姚兴佳等在传统直接转矩控制基础上,利用离散空间电压矢量调制技术,给出基于模糊控制策略的无刷双馈电机的直接转矩控制方法[2].侯晓鑫等提出一种低速高性能无刷双馈电机的直接转矩控制系统方案,采用双自由比例积分转速控制器,并对方案进行仿真实验[3].
以上研究均对无刷双馈电机直接转矩控制系统采取不同策略加以控制,取得了一定的控制成效,但仍存在电机转速波动大、转子转矩和磁链脉动幅度大、电机起动速度和转矩跟踪性能较差等问题,从而影响了无刷双馈电机控制系统的动静态控制品质和高效运行.为此,本研究提出基于神经网络和模糊逻辑的直接转矩控制策略,设计定子磁链神经网络观测器和逆变器开关状态模糊控制器,从而有效降低BDFM直接转矩控制系统的转矩脉动、速度脉动及磁链脉动,增强系统鲁棒性和控制性能.
1 无刷双馈电机数学模型
本研究中选取的无刷双馈电机为笼型转子无刷双馈电机.在d-q双轴坐标系中电机模型的电压方程、磁链方程、电磁转矩方程以及机械运动方程如数学表达式(1)~(4)所示.
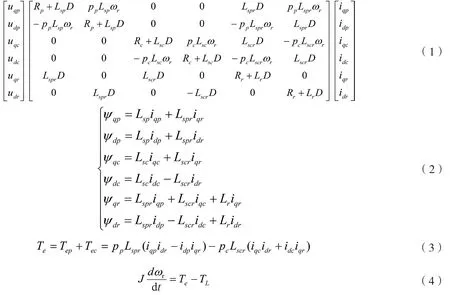
其中u、i分别表示电机电压、电流瞬时值;D为微分算子,下标s表示电机的定子侧,下标r表示电机的转子侧,下标d和下标q分别表示d-q双轴坐标系中d、q轴上分量;下标p和c分别表示电机的功率绕组和控制绕组,pp、Rp、Lsp分别表示电机功率绕组极对数、电阻值、自感值,Lspr为功率绕组与转子绕组之间的互感值;pc、Rc、Lsc分别为电机控制绕组的极对数、电阻值、自感值,Rr为转子绕组电阻值,Lscr为控制绕组与转子绕组之间的互感值,Te为电磁转矩,ωr为转子机械角速度;J为转子机械惯量,TL为负载转矩.
2 无刷双馈电机直接转矩控制系统
2.1 系统工作原理
BDFM直接转矩控制系统工作原理如图1所示.图1中,系统给定BDFM角速度为ωr*,检测的电机转子角速度为ωr;电机给定电磁转矩和测得的电磁转矩分别为Te*和Te;给定定子磁链为Ψs*,定子磁链在α、β轴上分量分别为Ψsα、Ψsβ,在α、β轴上电压分量分别为usα、usβ,在α、β轴上电流分量分别为isα、isβ,定子磁链位置角为θ.无刷双馈电机定子三相电流iA、iB、iC和三相电压uA、uB、uC,输入至电压电流检测单元检测并进行变换,分别得到两相电流isα、isβ和两相电压usα、usβ.再将两相电流和电压以及检测的电机角速度共同作为神经网络定子磁链观测器的输入量.然后经过神经网络的映射作用输出两相定子磁链Ψsα、Ψsβ.再利用磁链、转矩模型估算BDFM磁链、转矩以及定子控制线组磁链空间位置角.磁链模型和转矩模型的观测公式为:
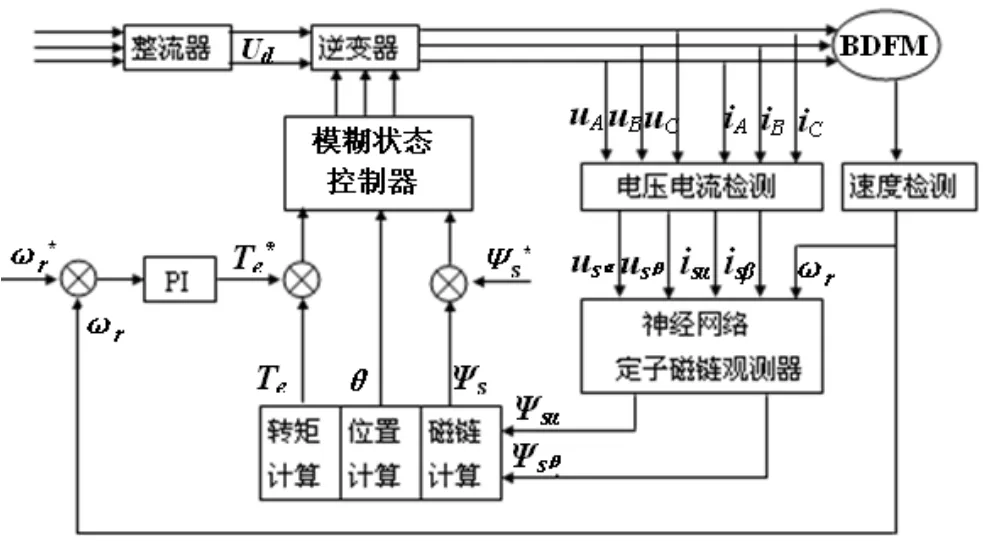
图1 BDFM神经网络模糊直接转矩控制系统结构


本系统中设计模糊状态控制器替代常规直接转矩控制中的磁链与转矩控制器.模糊控制器的输入量有3个,分别是电机的转矩误差e(TeT=Te*-T)e、磁链误差e(ψeψ=Ψs*-Ψ)s、定子磁链位置角θ.模糊控制器输出作用于逆变器,用于控制优化逆变器开关状态,利用逆变器控制BDFM定子三相电压、电流,根据控制要求输出转矩,实现电机调速.
2.2 神经网络定子磁链观测器的设计
2.2.1 神经网络结构
BDFM控制系统的定子磁链观测器采取典型的三层前馈BP神经网络结构,如图2所示.
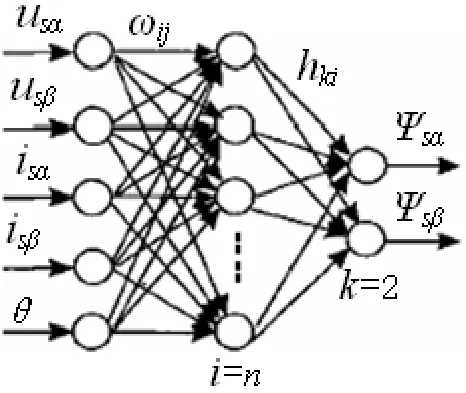
图2 神经网络结构
BP神经网络含输入层、隐含层及输出层.输入层有5个神经元节点sj(j=1,2…5),各节点分别对应输入BDFM定子两相电压、电流信号以及电机转子机械角速度,即usα、usβ、isα、isβ、ωr.隐含层的神经元个数根据网络学习需要进行确定,隐含层神经元节点数n一般与输入层、输出层的神经元节点数关系大,可通过经验公式n=(输入层神经元节点数+输出层神经元节点数)1/2+b计算得到.其中b选取1~10范围内的整数,n的确定还要综合考量网络定子合成磁链Ψs与给定磁链Ψs*的误差.通过多次试验,本设计中隐含层神经元节点数n选取7为宜.ωij为网络隐含层第i个节点(i=1,2…n)与输入层第j个节点的连接权值,隐含层神经元节点输出公式为[3]

式中θi为隐含层神经元节点阈值,Sj为输入层神经元,f1为隐含层神经元节点的激活函数.BP网络隐含层通常采取Sigmoid型函数进行中间结果的传递,f1函数表达式为

网络输出层有2个输出神经元节点Ok(k=1,2),输出节点分别对应两相定子磁链Ψsα、Ψsβ.设定输出神经元节点与隐含层神经元节点之间的连接权重为hki,输出神经元节点阈值为θk,输出层神经元节点输出公式为

式中f2为输出层激活函数,采用线性函数purelin作为输出层的传递函数,可以对输出进行值域扩展.
2.2.2 神经网络优化及训练
上述BP神经网络中含ωij、θi、hki、θk等结构参数,神经网络的学习过程实质上就是通过样本训练,按照BP神经网络学习规则和反向误差计算准则[4],通过不断调整网络的连接权值ωij、hki和阈值θi、θk,实现网络输出的均方误差最小化,直至网络输出满足目标精度.其中相关文献实验证明,ωij、θi、hki、θk的初始结构参数直接影响神经网络的学习过程与训练精度[5-6].所以,本设计中先对BP神经网络的初始结构参数利用蝙蝠-粒子群算法进行优化,然后再采取BP算法对BP神经网络加以训练.BP神经网络的初始结构参数优化及其训练主要步骤如下[7-8]:
step1: 设置蝙蝠-粒子群算法的初始化参数.蝙蝠算法中的蝙蝠数量为N,随机初始化蝙蝠位置为xi(i=1,2,…,N),最大迭代次数为NB,蝙蝠脉冲频率为f,最大脉冲频度为R0,脉冲频度增加系数为δ,最大脉冲声音强度为S,脉冲声音强度衰减系数为λ,粒子群算法中的最大迭代数为NP,最大、最小惯性权重分别为ωmax、ωmin.
step2: 更新脉冲频率fi、飞行速度vi、蝙蝠位置xi,寻找得到当前最优个体.
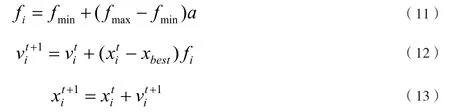
其中xit、vit、xit+1、vit+1分别是第i只在第t代和第t+1代时的位置和飞行速度;fi为第i个蝙蝠产生的脉冲频率,fmax、fmin分别为脉冲频率的最大、最小值,xbest为当前全局蝙蝠最优位置,a为0~1区间随机值.
step3: 产生随机数r1,如果r1>Ri,则从当前蝙蝠群中寻找到最优解且在附近随机生成一个局部解,更新蝙蝠的新位置公式为

式中的τ采用[-1,1]随机值,St表示平均脉冲声音强度.
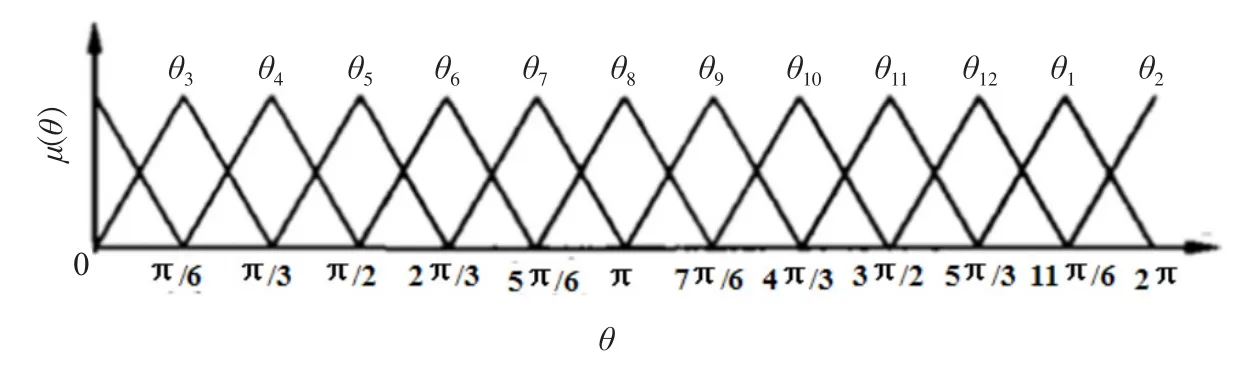
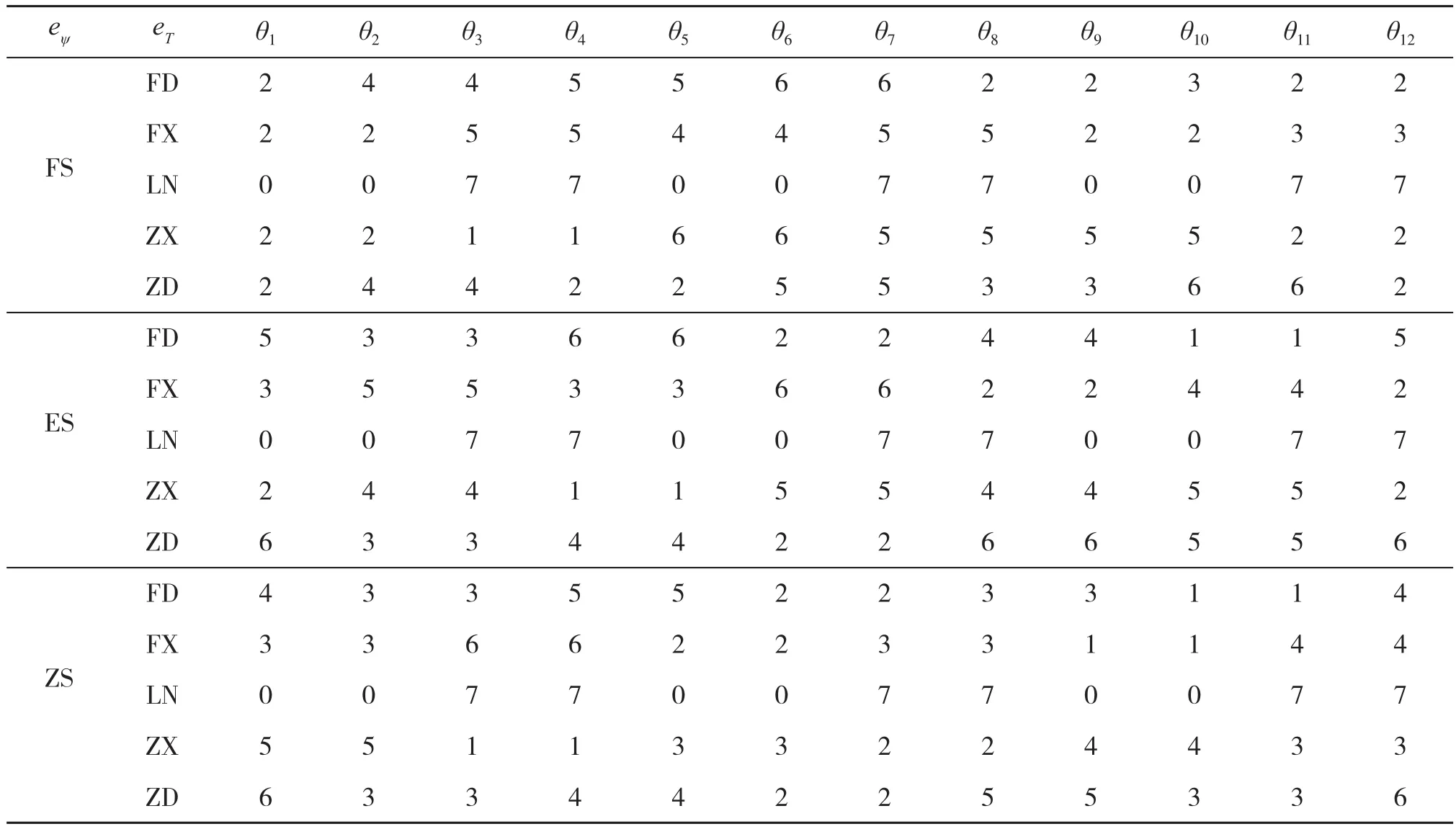
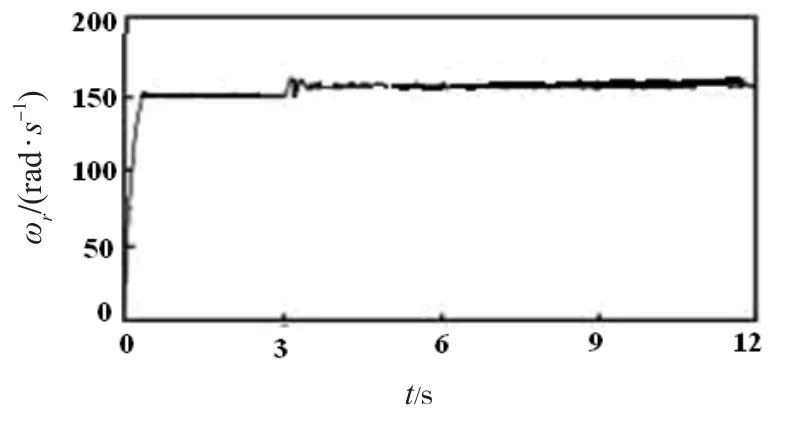
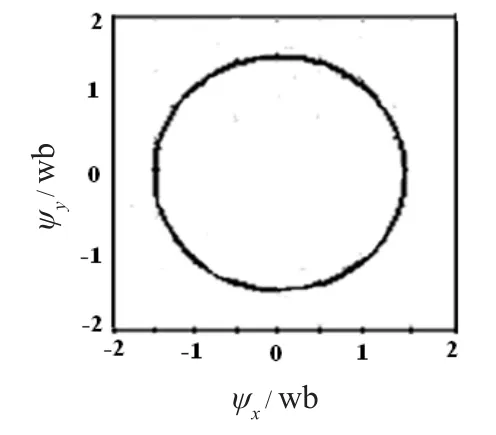
step4: 产生随机数r2,如果r2 式中Sit和Sit+1分别为第i个蝙蝠在第t代和第t+1代的声波脉冲响度;Rit+1为第i只蝙蝠在第t+1代时的脉冲频度;λ取值范围为 [0,1],δ>0. step5: 根据适应度J(xi)对蝙蝠个体加以评估,搜寻最佳位置个体.如果满足蝙蝠算法最大迭代次数NB,输出M个最优位置解,否则返回step2. step6: 将M个最优解组成粒子群初始种群,按式(17)~(19)更新粒子速度、位置. 式中i=1,2, …M,j=1,2, …d,t为粒子群算法的迭代次数;Xij(t)为粒子i位置;Vij(t)为粒子i飞行速度;Pj(t)为粒子i经历的最优位置,Gj(t)为所有粒子经历的最优位置;C1、C2为学习因子,R1、R2在[0,1]取值;J为粒子适应度值;Jave、Jmax分别为粒子群中平均适应度和最大适应度值. step7: 在粒子群算法的迭代数达到最大迭代次数,或者全局最优解Gj(t)<ε(ε为较小数值)时,则得到全局最优解. step8: 将全局最优解对应为神经网络最优初始连接权值和节点阈值,输入训练样本,利用文献[5]中提出的改进BP算法来训练神经网络,直到网络输出均方误差J达到最小时,便由神经网络输出得到磁链、转矩模型计算所需的两相定子磁链Ψsα、Ψsβ.这里均方误差(即适应度)J计算公式为 其中Qjk表示第j个训练样本在第k个输出节点处的期望输出,Yjk表示第j个训练样本在第k个输出节点处的网络实际输出,m表示BP神经网络输出节点数,n表示训练样本数. 神经网络优化及其训练流程示意图如图3所示. 图3 神经网络优化及其训练流程 模糊状态控制器用于控制和优化逆变器开关状态的选择.模糊控制器的输入量有3个,分别为磁链误差eψ、转矩误差eT和定子控制绕组磁链空间位置角θ.模糊控制器的输出量为电压空间矢量控制信号.eT、eψ以及θ均需要进行模糊化处理.转矩误差eT在其论域[-2,2]上定义5个模糊语言变量,即ZD=正大,ZX=正小,LN=零,FX=负小,FD=负大.磁链误差eψ在其论域[-0.02,0.02]上设定3个模糊语言变量,即ZS=正偏差,ES=零,FS=负偏差.定子控制绕组磁链空间位置角θ在其论域[0,2π]上定义12个模糊状态,即θ1~θ12.eT、eψ及θ的模糊语言变量的隶属度函数如图4、图5、图6所示. 图4 eT的隶属度函数 图5 eψ的隶属度函数 图6 θ的隶属度函数 根据模糊控制原理及系统控制要求,可确定180条控制规则,得到模糊控制规则如表1所示.模糊控制规则采用if—then语句形式表示,第i条规则为 表1 eT、eψ及θ的模糊控制规则 其中Ai为磁链误差,Bi为转矩误差,θj为控制绕组磁链位置角,Vk为电压空间矢量,即为模糊控制器输出,其论域为 [0,1,2,3,4,5,6,7],分别对应控制输出逆变器的8个开关状态,i=1~180,j=1~12,k=0~7. 利用Mamdani法计算最大隶属度对应的模糊控制器输出量,将其作为模糊控制器控制逆变器输出的电压矢量,即 式中i=1,2…180;μAi、μBi、μθj分别为模糊输入量Ai、Bi、θj隶属度;μVk为模糊控制器输出V的隶属度. 在传统直接转矩控制基础上,引入以上神经网络定子磁链观测器和逆变器开关状态模糊控制器的控制策略,运用MATLAB/Simulink建立无刷双馈电机直接转矩控制的仿真模型,仿真用BDFM参数设置情况如表2所示.优化训练神经网络的初始化参数为:蝙蝠种群数量N=200,蝙蝠脉冲频率f∈[0,1],脉冲强度、脉冲频度最大值分别为S=0.5和R0=0.65,脉冲强度衰减系数和脉冲频度增加系数分别为λ=0.45和δ=0.25,蝙蝠算法的最大迭代次数为NB=250.粒子群算法的最大迭代次数为NP=200,惯性权重最大和最小值分别为ωmax=1.75和ωmin=0.25,学习因子C1=C2=1.6.BP神经网络的目标误差精度为0.000 1,改进BP算法的最大迭代次数为680. 表2 BDFM仿真参数 图7、图8分别为常规直接转矩控制和本文提出的神经网络模糊直接转矩控制两种方案情况下BDFM电磁转矩、定子控制绕组磁链以及电机角速度的仿真曲线.从图中仿真结果对比分析可知,采取本文控制方法较常规直接转矩控制而言,转矩响应更趋平稳,转矩超调量及其脉动都很小,转矩脉动量由图7(a)的20 N·m降至图8(a)的10 N·m.定子控制绕组磁链瞬时幅值的脉动明显减少,由图7(b)的±0.26 wb降至图8(b)的±0.05 wb.电机角速度响应快速,图8(c)中角速度从电机启动达到50 rad/s过程仅用0.2 s,角速度由50 rad/s上升变化至120 rad/s也不足0.2 s,而且角速度波动变化幅度小,几乎无超调.所以,本文提出的神经网络模糊直接转矩控制系统动态和静态性能都显著优于常规接转矩控制. 图7 常规直接转矩控制仿真图 图8 神经网络模糊直接转矩控制仿真图 利用DSP芯片TMS320F28335作为系统控制核心部件,搭建无刷双馈电机直接转矩控制实验系统.系统试验的硬件电路示意图如图9所示[9]. 图9 系统试验电路示意图 通过霍尔传感器采集检测无刷双馈电机定子上的功率绕组和控制绕组的电压和电流值,利用增长量编码器检测BDFM角速度大小.逆变器选用三菱IPM智能模块PM150RLA120.由TMS320F28335控制芯片完成数据采集、神经网络的优化学习算法、模糊控制算法、PWM驱动信号输出等功能.DSP利用串行通信接口SCI与PC上位机进行通信,采用串行外接接口SPI与示波器相连接,PC机借助Labview图形化编程软件接收并显示BDFM角速度、转矩及定子控制绕组磁链等数据.本实验中,BDFM的转动惯量J=0.58 kg·m2.电机在空载情况下起动进入同步转速后,给定电机角速度为150 rad/s,当达到稳定运行状态后给电机增加50 N·m负载,电机运行一段时间后再卸掉该负载变为空载状态.图10~图12分别反映试验BDFM角速度、转矩及控制绕组磁链的数据变化. 图10 电机角速度响应曲线 图12 电机定子控制绕组磁链曲线 通过分析图10可知,BDFM空载起动约0.3 s后能迅速达到给定转速并稳定运行,起动时间短.在t=3 s时突加5 N·m负载,电机角速度大小波动非常小.分析图11表明,空载情况下起动时电机转矩为0,电机稳定运行后在t=6 s时增加50 N·m负载,电机转矩能迅速跟踪给定转矩,转矩脉动量较小.图12表征BDFM定子控制绕组磁链轨迹,磁链波形接近圆形.试验分析结果表明,本控制系统速度响应快,对于BDFM的角速度、转子转矩、定子控制绕组磁链的脉动变化均具有很强的抑制和削弱作用. 针对无刷双馈电机直接转矩控制过程中存在的转矩脉动、角速度脉动、磁链脉动等不足和问题,结合常规直接转矩控制的理论基础和控制思想,提出基于神经网络和模糊逻辑的直接转矩控制方法.该控制策略可以有效克服BDFM系统转矩、磁链、角速度脉动等方面的不足.系统具有较强速度响应、转矩响应及磁链特性,且鲁棒性强,动态性能可获得极大改善,是一种有应用前景的控制方案.
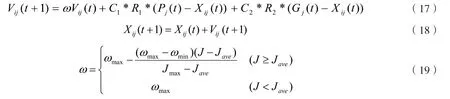

2.3 模糊状态控制器设计
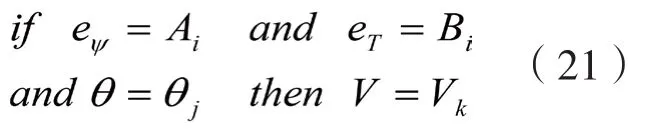
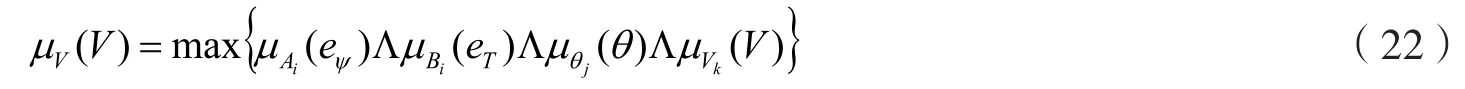
3 仿真分析
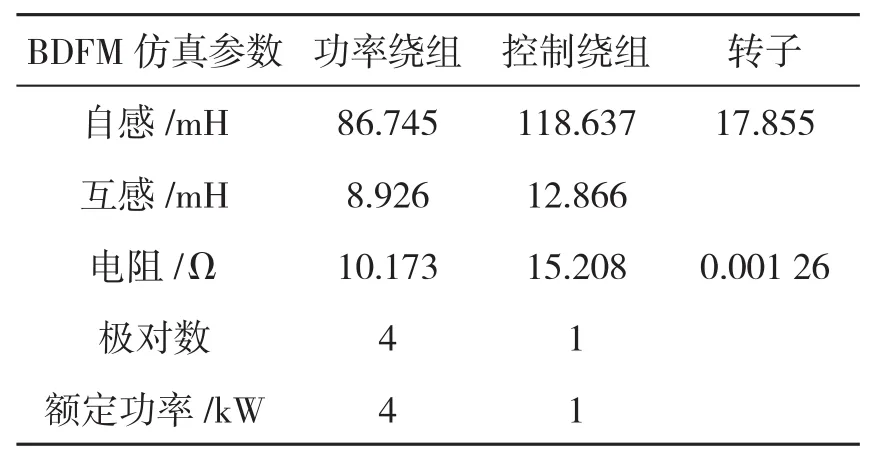
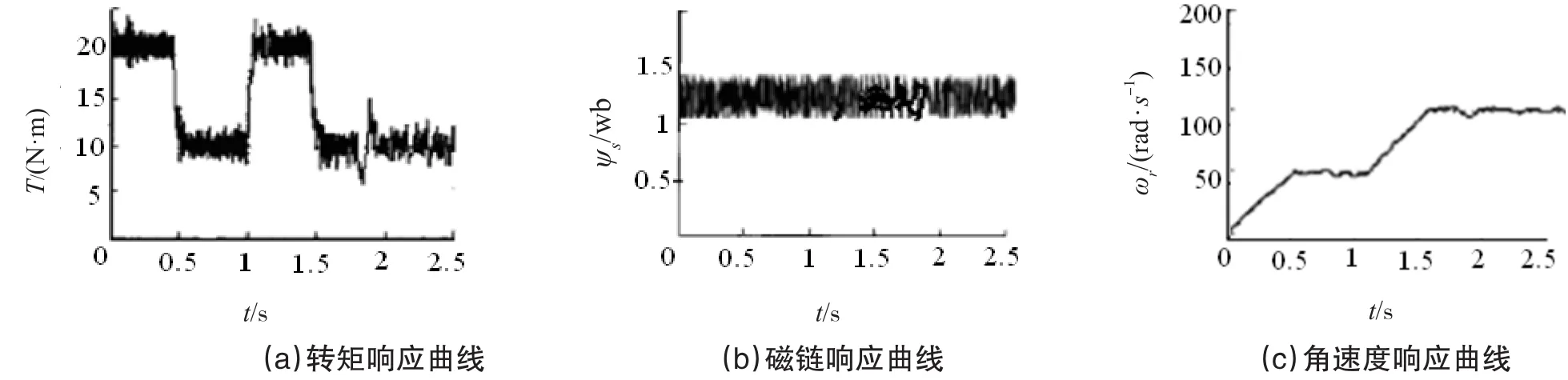
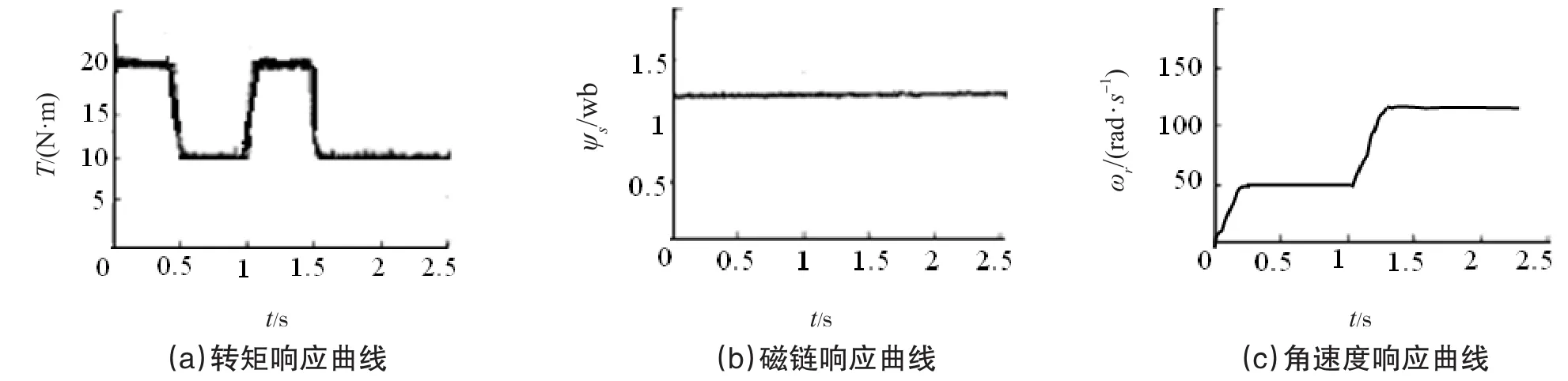
4 试验验证
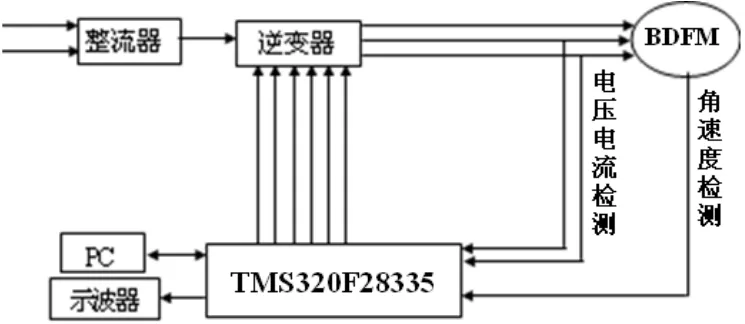
5 结语

