基于离线参数调整的古籍图像二值化算法

冯 炎，陈汝真

(西藏大学 信息科学技术学院，西藏 拉萨 850000)

0 引 言

图像二值化是古籍文档图像数字化修复的关键预处理步骤，同时图像二值化算法也是学者们研究的热点问题之一。Kovesi[1]提出了一种图像相位保持降噪方法，Nafchi等[2]的结果表明相位保持降噪方法能够提高图像二值化算法的性能。Lu等[3]提出了一种基于背景和笔划宽度估计的二值化算法，实验结果表明了该算法的有效性。Howe[4]提出了基于拉普拉斯能量的最优化全局能量函数计算方法，并采用图割算法分割文本和背景，接着，Howe[5]通过调整图像的关键参数设置来提高算法性能，但该算法对退化严重的古籍二值化效果不理想。Cheriet等[6]通过提取特征和最优参数，学习所提取特征和最优参数之间的关系，提出了基于学习框架的最优参数自动选择算法。Ballaprakash等[7]采用竞赛机制(racing algorithms)自适应调整算法中的参数设置，实验结果显示，该方法能够有效调整算法中的参数设置并取得了较好的结果，并用迭代弗里德曼竞赛机制(iterated fried man racing algorithms，I/F-Race)进一步改进了算法[7]。综上所述，虽然学者们提出了多种二值化算法，然而这些方法对于退化严重的古籍二值化效果仍然不理想[8]。I/F-Race方法能够调整算法参数，但该方法根据不同的应用场景有多种实现方式，主要体现在I/F-Race方法拟合函数选择、参数初始值设置、候选参数配置抽样方案和最优候选参数配置选择方法的不同。本文根据I/F-Race方法原理和Howe[5]的二值化算法存在的问题，设计了一种基于离线参数调整的古籍图像二值化算法。

1 本文的二值化算法

1.1 算法介绍

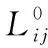
(1)

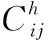
(2)

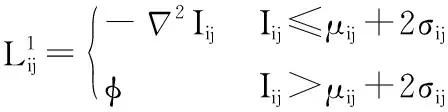
(3)

其中，μij和σij分别表示局部均值和局部方差，方差σij计算方法见Howe算法[5]，φ是一个较大的负数。

从实验结果得知，Howe算法[5]对退化严重的古籍图像二值化效果不理想，原因是Howe算法中μij是窗口半径为r的古籍原始图像局部均值，要求窗口半径r足够大并且至少是文本笔划宽度的几倍，然而，当r太大时所求局部均值会忽略局部细节，当r太小时局部均值又容易受局部文本像素的影响偏小，因此，Howe算法中的局部均值μij估计值不准确。根据图割算法原理分析得知，该均值应该是背景局部均值，而非背景和文本混合在一起的古籍原始图像局部均值。

1.2 背景局部均值估计方法

为解决Howe算法局部均值估计值μij不准确的问题，提出了一种背景局部均值μij估计方法，所提算法分为3步：第一，通过3种不同的降噪算法对退化古籍图像进行降噪，从而消除古籍背景信息并确定古籍文本区域，同时要确保降噪后的古籍图像文本召回率尽可能高；第二，将以上降噪结果作为背景修复模板并结合Ntirogiannis的图像修复算法[9]估计古籍背景；第三，用窗口半径为rc的高斯平滑算法进一步消除残留文本信息，从而获得较为准确的古籍背景局部均值估计值μij。

第一次降噪是采用窗口半径为ra的高斯平滑算法估计古籍背景，并对古籍图像I进行背景补偿从而去除大块背景噪声，降噪后的结果Ic计算方法如下

(4)

式中：gsmooth为高斯平滑算法。

第二次降噪是采用Kovesi提出的相位保持降噪[1]算法，该算法认为相位信息是图像中最重要的特征，使用非正交的复值log-Gabor小波提取图像中每个点的局部相位和幅度信息，同时保留感知上重要的图像相位信息，降噪过程是在每个小波尺度下确定噪声阈值，并在保持相位不变的前提下适当缩小滤波器幅度响应。用Kovesi算法对以上结果Ic进行降噪，从而去除文本附近的噪声，降噪后的结果Ik计算方法如下所示

Ik=kovesi(Ic)

(5)

式中：kovesi() 为相位保持降噪算法。

Lu等[3]提出的基于背景和笔划宽度估计的二值化算法是通过估计古籍图像背景来补偿古籍图像存在的退化现象，本文第三次降噪时采用了该算法思想。第三次降噪时先对以上结果Ik进行归一化，然后采用Otsu算法[10]对归一化后的Ik二值化，接着对该二值化结果进行数学形态学腐蚀操作来补偿二值化过程所丢失的文本信息，从而粗略确定文本区域并用Inoe表示，其中腐蚀半径为rb。最后去除第二次降噪结果Ik中除文本区域Inoe之外的背景噪声，用Ike表示，方法如下

Ike(i,j)=Ik(i,j)×Inoe(i,j)

(6)

接着，对Ike依次进行归一化、Otsu二值化[10]以及数学形态腐蚀操作来进一步去除背景噪声，得到最终降噪结果，从而确定文本区域，其中腐蚀半径为rb。

算法过程演示如图1所示，示例图片选自H-DIBCO 2018数据集[11]。从图1可以看出，与Howe算法相比，本文算法更能够体现背景细节，同时本文算法所估计的背景局部均值包含文本信息相对少一些。

图1 背景局部均值估计结果对比

2 算法关键参数离线调整方法

2.1 参数离线调整方法

竞赛机制可以解决有多种候选解的问题，该方法执行时需要从给定的实例集选取一些训练实例，每个候选解都在相同的实例上进行计算，在竞赛过程中淘汰表现差的候选解，该方法也可以解决从一组候选算法参数中选择最优参数的问题。算法参数调整问题被视为泛化问题，就像在其它领域(例如机器学习)一样，根据给定的一组训练实例集，目标是确定算法参数配置使其在不可见的测试实例上性能表现最优。Ballaprakash等[7]采用竞赛机制算法思想提出了一种算法参数调整方法，该方法是在特定的训练实例上对候选参数配置依次进行测评，淘汰远远落后于当前的最优参数的某个候选参数配置，其中，最优参数是在竞赛过程的某一个阶段表现最好的候选参数。I/F-Race[7]采用迭代弗里德曼竞赛机制进行离线算法参数设置，算法使用弗里德曼检验，在给定的训练实例上对每个候选参数配置的评估性能进行排序并计算秩次和，用以决定在某一给定步骤中需要删除哪些候选参数配置，并且在每次迭代中，新采样的候选参数配置都会偏差于先前迭代中尚存的候选参数配置，以此方式将候选参数配置的采样集中在性能较优的参数配置周围。但是I/F-Race方法中拟合函数、参数初始值设置和候选参数配置采样方案需要根据不同的算法应用做相应的调整。本文根据Mesquita等对I/F-Race的解释[12]给出二值化算法的参数配置调整方法，并根据本文二值化算法的特点重新设计了I/F-Race中的参数初始值设置、候选参数配置抽样方案和最优候选参数配置选择方法。

参数离线调整算法包含离线训练和测试两个阶段，离线训练时，在有限的时间内通过给定实例集确定最优参数配置，使得算法以某种度量标准达到性能最优，训练实例集尽可能包含测试阶段遇到的各种实例，以期得到最优结果，然后在测试阶段，算法采用训练所得参数在一组实例上执行。为了清楚起见，假设本文二值化算法具有d个需要调整的参数，每个参数的所有可能值之间的组合称为参数空间X，我们的目标是从参数空间X中通过某种抽样方法选择一种配置H使得给定的评价函数δ在实例集I上取值最小或最大化。参数离线调整方法具体实现分为3个步骤：第一，采用正态分布作为抽样概率分布模型，并采用本文提出的候选参数配置抽样方法从参数空间X中抽取新的参数配置；第二，通过竞赛方法从所抽取的参数配置中选择最优参数配置；第三，更新概率分布模型方差，使下一次迭代时候选参数配置抽取偏向更好的参数配置。重复执行这3步直到满足终止条件。

2.2 候选参数配置抽样

在第一次迭代中，初始候选参数配置集H0是通过从参数空间X中均匀抽取得到，之后的迭代中，从参数空间中重新采样候选参数配置。用Ns表示固定的候选参数配置数，在参数离线调整每次迭代中，对经过F-Race方法通过竞赛选择幸存下来的最佳的Nelite个候选配置，重新采样Ns-Nelite个新的候选参数配置。新的候选配置会围绕最佳配置进行采样，以便能够发现更好的参数配置值。前一次迭代尚存的候选参数都有偏差于新采样的候选参数，也就是说新的候选参数是围绕前一次尚存的候选参数周围的其它参数采样。

具体方法如下，首先对最佳的Ns个候选配置，标出其在每个实例的评估结果秩次，然后，根据秩和从小到大排序，根据其秩rz(z=1，…，Ns) 对这Ns个精英配置进行加权，权重wz与其秩成反比，计算方法[12]如下

(7)

然后，需要循环Ns-Nelite次来采样每个新的候选配置，每次循环时需要按权重随机从最佳的Ns个候选配置中选择一个较优参数配置，假设随机选择一个较优参数配置为Xi，在较优参数配置两旁即边界为Xi∈[(Xi-Xi-1)/2,(Xi+1-Xi)/2] 的区间根据采样概率分布模型随机采样一个值。若采样的参数与已采样的参数相同则重新采样，若重复10次无法采到找新的值则结束循环。

2.3 最优候选参数配置选择

本文采用基于弗里德曼竞赛机制的F-Race算法[12]进行最优候选参数配置选择。用Ii表示第i个实例，Hk表示竞赛中在迭代k时仍然存在的候选配置。在F-Race第k次迭代，竞赛机制顺序将所有采样候选参数配置在实例集I中每个实例Ii上执行一次。

当候选参数配置Hk中的每个参数在单个实例Ii上评估时，首先要查找该参数是否在上一次F-Race迭代中运行过，若上一次F-Race用同样的参数和实例执行过，则取上一次的结果，否则执行性能评估运算，当评估完成后，需要根据弗里德曼测试方法对评估结果进行统计检验，来确定某些参数配置在实例Ii上的评估结果是否存在显著的性能差异，如果有足够的数据证明候选参数配置Hk中的某几个参数配置的性能要差别于其它参数配置，该参数配置会被删除。剩余的候选配置将继续在下一个实例中运行，若淘汰后剩余参数个数小于Nstop则F-Race提取结束。这个程序执行直到所有实例执行完后，对性能评估结果按相对秩和从小到大排列(按从优到差)，若结果个数大于Nmax，则取前Nmax个。

2.4 概率分布模型更新方法

为了获得更好的抽样值，在参数离线调整方法每次迭代中都需要更新抽样概率分布模型，抽样概率分布模型为正态分布。而抽样概率分布的方差std根据参数离线调整方法迭代计数器k的增加而减少，这样就可以使候选配置越来越集中在性能最好的配置上，std计算方法如下[12]

std=1-2×k/10

(8)

3 实验及结果分析

3.1 实验环境及评价方法

本文实验训练数据和测试数据采用了H-DIBCO 2016[13]和H-DIBCO 2018[11]提供的古籍图像数据集及相应的基准图像，这些图像数据集是具有不同退化类型的古籍图像，使用这些数据集可以检验本文所提算法是否有效。

实验采用了主观实验演示和客观实验评价对本文算法进行评估。客观实验采用了DIBCO[11]推荐的评价方法，具体是精确度(Precision)、峰值信噪比(peak signal to noise ratio，PSNR)、F值(Fmeasure)、距离倒数失真度量(distance reciprocal distortion，DRD)和错误分类处罚指标(misclassification penalty metric，MPM)5种图像客观评价指标。其中，Precision是指二值化结果所含文本像素个数的比例即正确率，指标值越大说明算法精确度越高；PSNR是一种基于对应像素点间的误差质量评价方法，该值越大说明图像二值化效果越好；Fmeasure是可以兼顾准确率和召回率的一种图像二值化评价方法，该值越大说明结果越接近基准图像；DRD是一种图像失真度评价方法，该值越小说明图像二值化结果失真越小；MPM是惩罚错误分类像素的方法，值越小表示错误分类越少。

实验选取了HoweAlg1[5]、HoweAlg3[5]、Niblack[14]、Bernsen[15]和Otsu[10]5个有代表性的二值化算法与本文算法进行比较，其中，HoweAlg1和HoweAlg3是Howe[5]提出的两种不同的二值化算法，本文算法是在HoweAlg1算法的基础上做的改进。

本文算法采用的保持相位降噪和边缘检测算法参数根据参考文献设置[5]：k=1，nscale=5，mult=2，norient=3，softness=1，thi=0.4，tlo=0.1，sigE=0.6。本文局部背景均值古籍算法中的参数ra根据实验设置：ra=20，而参数rb和rc是本文的关键参数，需要根据参数离线调整方法设置，根据该方法实验结果：rb=3，rc=3，意味着本文所估计的古籍背景局部均值是半径rc=3的窗口内的均值。

离线参数调整算法所需参数需要根据参考文献[12]和本文算法实际情况进行设置，参数说明如下：d是需要优化设置的参数个数；X是算法使用的候选参数空间，即为所有可能的参数组合，本文有两个关键参数，每个参数取值范围都是1，2，…10，可能的参数组合有100个；I是训练实例集，本文选了10个具有代表性的训练样本集合；Ns是通过实验定义的抽样候选参数配置的数量；δ是拟合函数，采用Fmeasure为拟合函数来评估二值化算法性能；Max_iter是I/F-Race最大迭代次数；Nstop是每次迭代中F-Race终止条件；Nmax是竞赛过程中保留的最大的最优参数个数。具体设置如下：d=2，Ns=16，Max_iter=2+log2(d)，Nstop=2+log2(d)，Nmax=0.5×Ns。

3.2 实验结果分析

本文在表1中给出了各二值化算法在H-DIBCO 2016数据集中10幅古籍图像的二值化结果平均值对比，其中，Precision、PSNR和Fmeasure值是越大越好，而DRD和MPM值是越小越好。如表1所示，本文的算法的5种评价指标即Precision值、PSNR值、Fmeasure值、DRD值和MPM值都是最优，其它几个二值化算法各有优劣，充分说明了本文算法的性能不仅优越而且稳定。

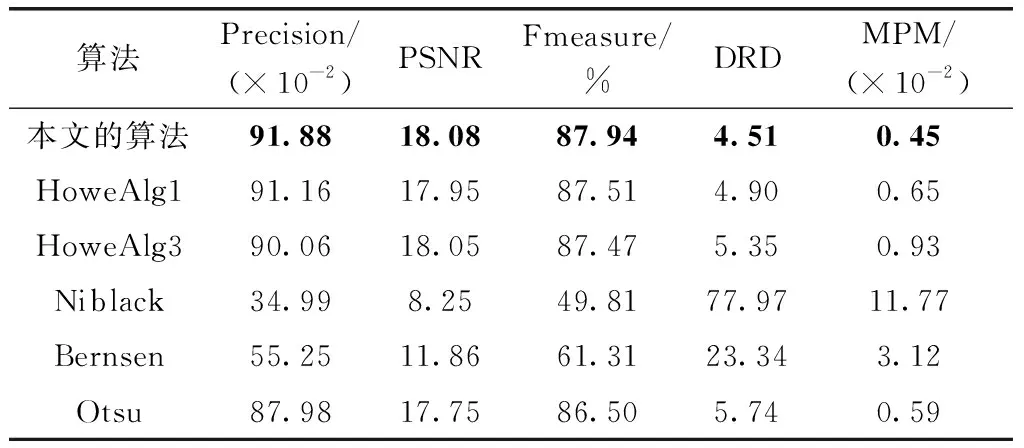
表1 各二值化算法在H-DIBCO 2016数据集的结果

表2中给出了不同二值化算法在H-DIBCO 2018数据集中10幅古籍图像二值化结果的平均值对比。如表2所示，本文算法的各项性能指标均是第一，HoweAlg3次之，HoweAlg1排第三。与次优HoweAlg3算法比较，本文算法的Precision值、PSNR值和Fmeasure值分别提高了12.33%、8.27%和4.48%，值得一提是本文的DRD值和MPM值分别降低了47.28%和66.21%。

表2 各二值化算法在H-DIBCO 2018数据集的结果

从表1和表2的实验数据可以看出，本文算法的5种性能指标均优于其它二值化算法，充分表明本文算法可以处理多种退化类型的古籍图像，同时表明本文图像二值化算法可以有效降低图像失真度和分类错误率。

为直观显示本文算法的优越性，从H-DIBCO 2018选取了1幅具有代表性的测试图像，该图像是一幅退化严重的古籍图像，并在图2中给出了不同二值化算法结果对比。从图2可以看出，HoweAlg1以及HoweAlg3算法处理效果较满意，但仍有部分残留噪声，尤其是边缘部分的噪声；

图2 不同二值化算法结果对比

Otsu算法在对比度较高的区域内二值化效果较好，但对于退化严重的低对比度区域效果较差；Niblack算法和Bernsen算法残留噪声太多，更容易将背景污渍误判为文本；本文提出的二值化算法结果最接近基准图像，并且能够很好地解决退化严重的古籍图像中存在的背景噪声干扰问题。

4 结束语

学者们常用I/F-Race方法离线调整算法参数，但该方法需要根据不同的应用场景设计相应的实现方式。本文根据I/F-Race方法原理和Howe算法存在的局部均值估计值不够准确的问题，设计了一种基于离线参数调整的古籍图像二值化算法，所提算法分为两步，一是估计古籍图像背景局部均值，并结合基于拉普拉斯能量的二值化算法对古籍进行二值化，二是根据I/F-Race算法设计了一种离线参数调整方法来优化本文算法中的参数配置。本文的背景局部均值估计算法是通过3种不同的降噪算法对退化古籍图像进行降噪，并结合图像修复算法及高斯平滑算法来估计古籍背景局部均值。实验结果显示本文算法可以处理多种退化类型的古籍图像，并且可以有效降低图像失真度和分类错误率，验证本文所提算法的有效性。