基于蚁群算法求解VRPTW 路径规划问题研究

魏子秋，孙明哲

（河北科技大学 经济管理学院，河北 石家庄 050018）

0 引 言

在1959 年，Dantzing 和Ramser 在经过实验和思考后，首次提出配送车辆路径优化问题。在物流运输中配送是重要的环节，准确选择配送车辆路径能有效缩短运输时间、降低运输成本、满足顾客需求等目的。

关于寻找最优配送线路问题已经成为研究的热点之一。最初蚁群算法是研究旅行商的问题，现在已经广泛应用到许多寻找最优解的问题中。例如：郑娟毅等利用蚁群算法寻找配送车辆路径最优的问题，张银玲等利用蚁群算法寻找移动机器人的最优路径，鲁丰玲、白俊强等通过蚁群算法寻找无人机最优路径，蚁群算法被应用到解决旅游最优路线的问题中，Wang Yong 等利用蚁群算法解决VNF 布局网络问题，张肖琳等在绿色环保角度，对油耗、污染物排放等因素进行约束构建路径优化模型，利用蚁群算法找出最优路径。可以看出蚁群算法虽然可以解决许多实际问题，但还存在不足，于是提出最大最小蚂蚁系统以及混合蚂蚁系统等方法，都在一定程度上提高了运算效率。虽然大多数文献已经对路径优化进行了充分研究，但本文结合时间窗约束建立总成本最小、总行驶距离最短、碳排放量最低的多目标优化模型，通过蚁群算法对设置的参数和约束条件进行求解，得出最优的配送路线。

1 物流配送路径模型

该问题的一般提法是：已知配送中心的横、纵坐标，所有客户的横、纵坐标和需求量，车辆必须从配送中心开始出发对每个客户进行配送，对每个客户进行配送完毕之后再回到配送中心，在车辆额定容量和行驶距离等约束条件下，使得目标（如成本最少、路程最短等） 达到最优。在实际情况中，除了成本外还要考虑其他许多因素，车辆路径优化问题大多数都是多目标优化，求解难度更大，所以研究带有时间窗的路径优化问题意义重大。

1.1 问题的描述

已知某物流公司的配送中心及客户的横、纵坐标，同时由相同属性（油耗、载重、速度） 的车辆从配送中心出发向各自回路中的客户进行货物配送，配送完毕之后再回到配送中心，每个客户所需的货物量不超过车辆运载能力，并且每个需求点只能在配送时间窗内由一辆车配送，每辆车所服务的客户需求之和不超过车辆的载重量。

在实际情况下，为达到配送中的总运输成本最低、总行驶距离最短、碳排放量最低等目的而提出的问题。

1.2 建立多目标数学模型

1.2.1 参数和变量

由此建立数学模型，用O 表示配送中心仓库；有n 辆相同的车辆，给每条回路上的I 个客户提供货物；用a表示车辆的固定成本；用N 表示确定所需的车辆数目，每辆车的编号为i，并且只在一条回路上行驶；用a表示车辆在客户j 和k 的配送过程中所产生的运输成本；用b表示客户点j 和配送中心O 之间的产品总量；每辆车i 的路径为c；车辆i 服务于客户j 为c；用I=0 表示车辆i 没有可服务的客户；用d（）表示在车辆i 的配送回路中，两个相邻客户所配送需要的路程；用d（）（）表示车辆i 从第I个客户行驶到配送中心O 的距离；用d表示客户j 和k 之间的距离；用e表示车辆i 配送结束之后回到配送中心所剩下的货物总量；用L表示车辆i 行驶的最远路程；用p 表示车的碳排放量；用Q表示在车辆i 的回路中，客户j 所需要的货物量；用w表示车辆i 的额定载重；用ET表示车辆i 分别给客户j 最早的配送时间；用LT表示车辆i 分别给客户j 最晚的配送时间；用WT表示车辆i 从客户j 出发的时间；用RT表示车辆i 到达客户j 的时间；用α 和β 分别表示硬、软时间窗惩罚成本系数；用UT表示车辆i 对客户j 所服务的时间；用T表示车辆i 从客户j 配送完毕后，再出发到客户k 所耗费的时间；用v表示车辆在配送过程中的速度；用S 表示所有车辆进行配送的总路程；用Z 表示所有车辆在配送过程中的运输总成本；用F 表示所有车辆总的碳排放量水平。

为了满足客户点j 设置的配送时间窗，在对客户点j 进行配送时，配送车辆到达时间RT必须满足下式：ET≤RT≤LT；

配送车辆i 在客户j 到k 间行驶的时间：T=d/v；

配送车辆i 从客户j 出发抵达下一个客户点k 的时间：RT=WT+UT+T；

时间窗惩罚函数系数用集合H 表示：H=[α, β ]。

1.2.2 目标函数

由描述的问题和分析可知，在进行物流配送时应首先考虑总成本最小，其中包括运输成本、车辆固定成本、违时惩罚成本；同时又要考虑最优路径的选择和碳排放量最低，从而得到多目标函数：

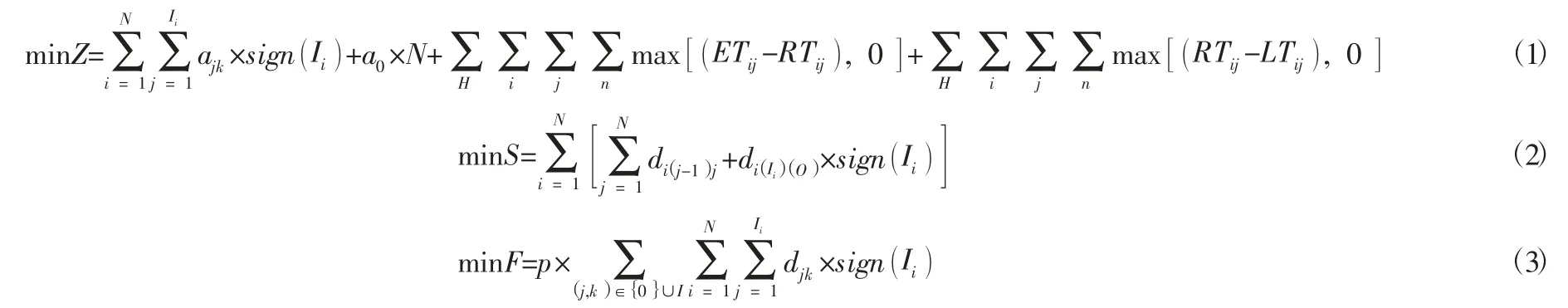
目标函数（1） 表示使车辆在最佳运输路径上的运输总成本最小（前两项为运输成本，后两项为惩罚成本）；目标函数（2）表示使车辆对所有客户完成配送并返回配送中心后，进行配送的总路程最短；目标函数（3） 表示使车辆的排放量降到最低，以降低环境污染。

1.2.3 约束条件

对上述目标函数进行约束：

约束条件（4） 表示为车辆的容量条件，每辆车所装载的货物在小于等于额定载重量的情况下，满足相应回路中客户的总需求；约束条件（5） 表示每个子回路中的车辆配送路程不超过所有车辆总配送路程；约束条件（6） 表示配送车辆在各自的回路中所服务的客户不超过客户总量；约束条件（7） 表示所有需求车辆所服务的客户总数等于实际的客户总数，保证所有客户都能得到服务；约束条件（8） 表示每辆车所服务客户的集合；约束条件（9） 表示每个客户被有且仅有一辆车所服务；约束条件（10） 确保所有运行车辆空车返回配送中心；约束条件（11） 表示第i 辆车是否参与服务；约束条件（12） 表示有进行配送任务的车辆数要小于等于总的车辆数；约束条件（13） 表示车辆在符合相应客户的时间窗内进行配送。

2 蚁群算法

Marco Dorigo 通过对蚂蚁群体觅食的研究，随后在1992 年提出蚁群算法（Ant Colony Optimization, ACO），它是一种模拟仿真寻找最优路径的算法，该算法具体是模仿蚂蚁在寻找食物过程中分泌一种特殊的可随着时间的推移而挥发的信息素来引导其他蚂蚁选择此路径的行为，经过一段时间后寻找到最优路径的目的。

2.1 参数设置

蚁群算法中有最基本的6 个参数：用m 表示蚂蚁的总数；用Q 表示蚂蚁一次循环释放信息素的总量；用t 表示在运算过程中最大的迭代次数；用α 表示信息素因子；用β 表示启发函数因子；用ρ 表示信息素挥发因子。

2.2 构建行动路径

在构建路径的过程中，用轮盘赌法选择蚂蚁要到达的下一座城市。计算公式如下：

式中：用i 表示起点，j 表示终点；η（t ）=1/d表示i 和j 之间距离的倒数，η（t ）是启发函数；用τ（t ）表示在时间t 时刻，起点i 到终点j 之间所包含的信息素浓度大小；用allowed表示蚂蚁k 还没有到达过剩下城市的集合；此路径上的信息素浓度大小由两地距离长短控制，两地距离越短，信息素浓度越大，选择此路径的几率就会越大，反之，距离越远浓度越小；从公式可以看出信息素因子α 决定信息素浓度，启发函数因子β 决定转移期望对蚂蚁k 从i 到j 可能性的贡献程度。

2.3 更新信息素

蚂蚁释放的信息素具有随着时间挥发的特性。因此，在每一次迭代完成后，都要将蚂蚁所带来的相关信息和信息素浓度进行更新，规则为：

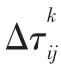
式中：L表示蚂蚁k 所经过的所有路径之和。

2.4 判断迭代是否终止

是否达到迭代次数可以判断仿真实验是否终止。一次迭代就是指m 只蚂蚁都走完所有的路径，即存在m 个搜索路径。在所有的路径中选择最短的路径，做出这一次迭代的可视化结果，更新信息素；然后将新的最短路径与上一次的最短路径进行对比，同时增加1 次迭代次数；最后计算当前迭代次数与最开始设置的迭代次数相差多少次，若正好相等则停止迭代，否则进行下一次迭代。

3 仿真实验

某配送中心（编号0） 有额定载重为1 000kg 的配送车辆6 辆，需在42 天内（1 008h） 将货物派送至19 个客户点，从0～19 依次对配送中心仓库和19 个客户点进行编号，其中配送中心以及各个客户点之间的横、纵坐标，客户的需求量、左时间窗、右时间窗和所对应的服务时间如表1 所示。

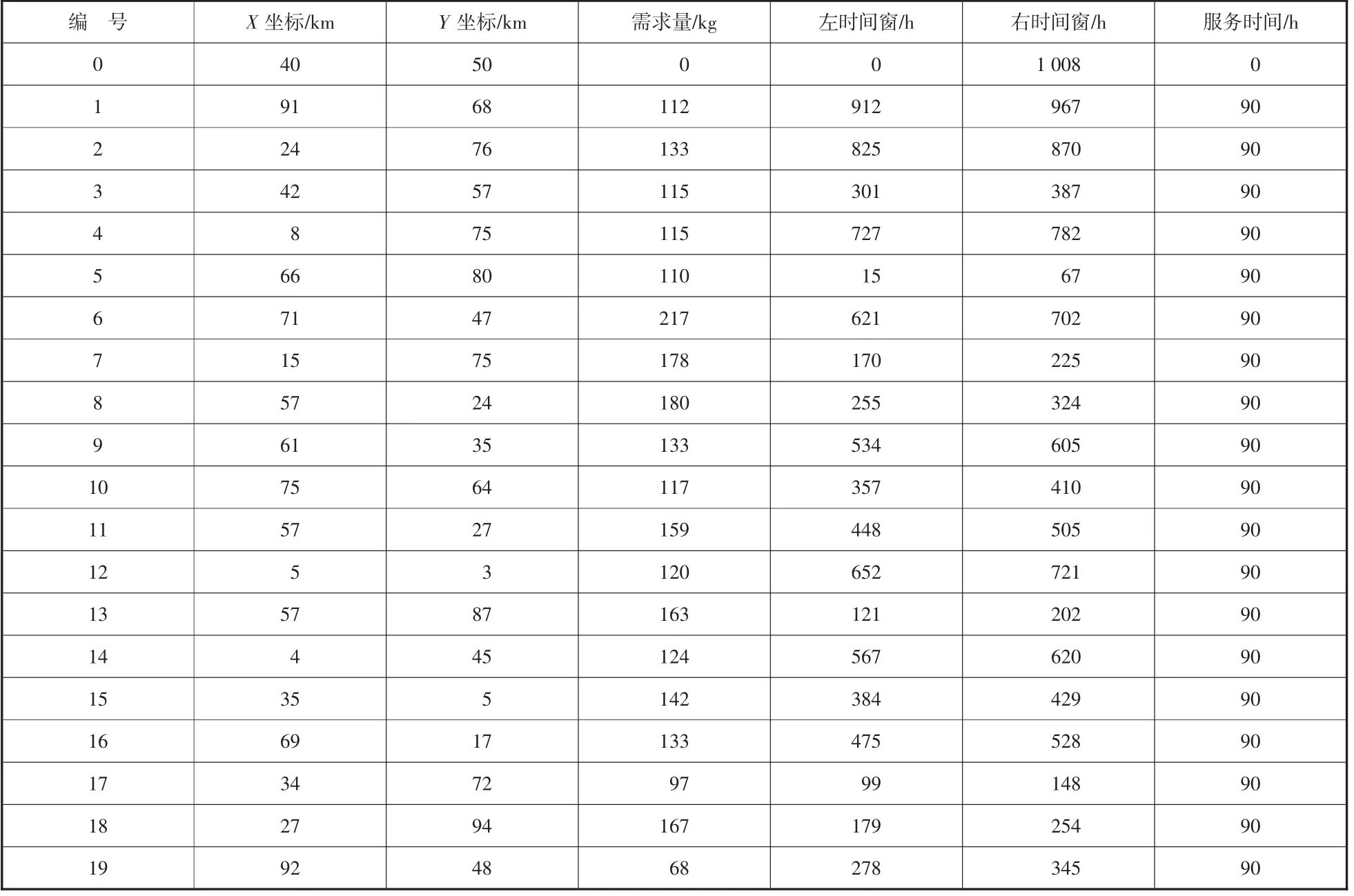
表1 坐标及货物需求量

将表1 中的数据换成矩阵形式后，导入到MATLAB 中，并且对算法中的参数进行多轮假设，得出最优的参数数值为：蚂蚁总数量m=35，释放信息素常量Q=100，运算最大迭代次数t=100，信息素因子α=1，启发函数因子β=3，信息素挥发因子ρ=0.4，等待时间重要程度因子γ=2，时间窗跨度重要程度因子δ=3。

对参数设置完毕后，将表1 中数据与参数值同时输入到程序中，经过100 次仿真实验，得到6 种结果，其中798.4072km 为最优路径，计算过程如表2 所示。

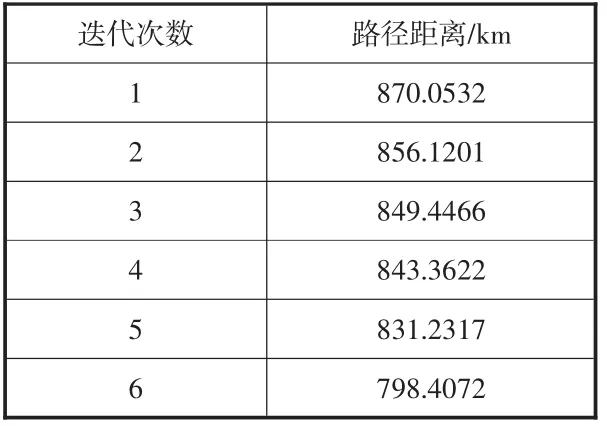
表2 6 次路径距离计算结果

得出4 条车辆最优配送回路路线：

配送路线1：0→5→13→19→10→14→12→2→0，运输量为835kg；

配送路线2：0→17→18→3→11→9→6→1→0，运输量为1 000kg；

配送路线3：0→7→4→0，运输量为293kg；

配送路线4：0→8→15→16→0，运输量为455kg。

4 条配送回路路线如图1 所示：

图1 为MATLAB 运行出的相对最优配送路径，蓝点为车辆配送中心，蓝色线为配送路线1，红色线为配送路线2，绿色线为配送路线3，橙色线为配送路线4。

图1 最优配送路径图

在原始的算法中没有对顾客服务时间的约束，会增加惩罚成本并且大幅降低顾客满意度，此方法将配送车辆在时间约束下计算出相对最优的路径，更好地降低物流成本，提高客户满意度等优势。可见，带有时间窗的蚁群算法更加符合企业的成本控制和顾客的需求，使该模型的配送效益最高，适用性更强。

4 结 论

如今我国的物流产业正在进行迅速的发展，但不可避免会出现成本控制等问题，所以合理规划最优路径以降低成本显得尤为重要。此方法在车辆的行驶距离、物流成本、碳排放量等目标基础上，做了数学优化模型，并利用MATLAB运行带有时间窗的蚁群算法寻找车辆的最优路径，达到车辆行驶距离、运输成本、碳排放量最低的目标，此计算结果在一定程度上对实际情况有参考价值。