不同设计参数对矮塔斜拉桥受力及变形的影响研究

作者简介：

陈金梅（1983—），工程师，主要从事建设管理工作。

摘要：文章以某双塔混凝土矮塔斜拉桥为研究对象，通过运用Midas Civil有限元软件建立实桥数值模型，对不同主梁刚度比、边中跨比、无索区长度情形下斜拉桥的主梁受力及变形影响规律进行研究。结果表明：（1）随着主梁刚度比的增大，矮塔斜拉桥主梁中跨、边跨的最大挠度均逐渐减小，而主梁中跨、边跨的最大弯矩逐渐增大，但主梁边跨弯矩增幅不明显;（2）矮塔斜拉桥主梁边跨的最大挠度、最大弯矩均随着边中跨比的增大逐渐增大，而中跨的最大挠度、最大弯矩则随之逐渐减小，且中跨的最大弯矩减幅缓慢;（3）随着边跨无索区长度的增大，矮塔斜拉桥边、中跨最大挠度和最大弯矩均逐渐增大，但边跨弯矩增长幅度不明显。

关键词：矮塔斜拉桥;主梁刚度比、边中跨比、无索区长度;变形;受力

中国分类号：U448.27A361323

0 引言

由于矮塔斜拉桥具有跨距灵活、外形美观、施工简捷、经济合理等优点，故在我国桥梁工程建设中得到广泛的应用[1]。据调查统计，现有部分矮塔斜拉桥因早期设计考虑不足，使得桥梁产生了变形、受力不均等病害，而如何有效保证矮塔斜拉桥的安全稳定，成为现阶段桥梁设计工作者需要重点考虑的课题[2-4]。

近年来，国内外学者在斜拉桥设计问题方面进行了大量的研究，如鲍英基等[5]对PC斜拉桥运营阶段主梁的应力和位移进行敏感性分析，得出主梁应力和位移随各参数的变化规律，为该桥梁运营养护管理提供借鉴和參考;牛伟迪[6]以神农湖大桥为研究对象，阐述了独塔斜拉桥的总体设计思路，分别对主桥整体与索塔锚固系统展开了静力分析，认为该桥的索塔锚固系统设计合理且整体结构满足规范要求;卫康华等[7]通过计算比较各设计参数在成桥状态时对主梁线形、应力、成桥索力和主塔偏位的影响，发现主梁容重、拉索初张力、季节温差和索梁温差为主要设计参数，而混凝土弹模、日照温差和索塔两侧温差对成桥状态的影响较小，为次要参数;李德旭等[8]采用有限元分析方法，设计了4种主塔横梁设置方案，从斜拉索受力、主梁变形及应力、主塔变形及应力方面进行定性分析，发现混凝土无背索斜拉桥主塔上横梁的设计十分必要。考虑到有关矮塔斜拉桥设计参数的影响研究较为欠缺，笔者以某矮塔斜拉桥为研究背景，通过借助Midas Civil有限元软件，分别对不同设计参数情形下的矮塔斜拉桥受力及变形规律进行了系统研究，以期为同类矮塔斜拉桥工程的设计工作提供参考与借鉴。

1 项目概况

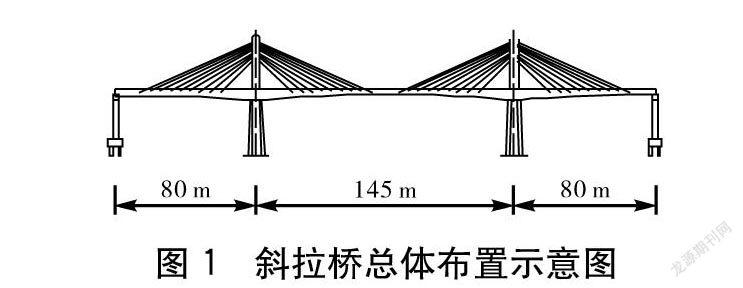
某双塔混凝土矮塔斜拉桥跨径为（80+145+80） m，桥宽为25.25 m，其中包括行车道宽为2×11.25 m，防撞护栏宽为2×0.5 m，中央隔离带宽为2 m。桥梁车道采用双向六车道设计，设计速度标准为80 km/h，设计荷载为公路-Ⅰ级。该斜拉桥上部结构采用单箱三室斜腹板变截面箱梁，其顶板、底板分别宽为12 m和6.8 m，支点处与跨中处梁高分别为5.8 m、2.8 m，在斜拉索张拉范围处的箱梁内每隔6 m设有一厚度为0.4 m的横隔板。该斜拉桥的主梁、塔间采用塔梁固结体系形式，主塔采用截面尺寸为5 m×2.4 m的矩形断面，桥面以上塔高为24 m。主塔上17对斜拉索呈单索面扇形对称布置，其梁与塔上间距分别为7 m、1 m，边中跨无索区的长度分别为18 m、21 m。斜拉桥的整体布置情况如图1所示。

2 有限元模型的建立

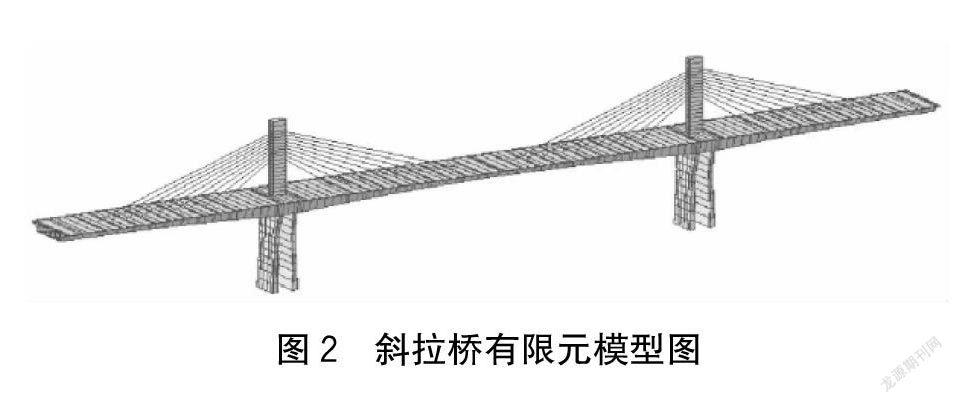
通过借助Midas Civil有限元软件建立该矮塔斜拉桥的三维数值模型。模型中矮塔斜拉桥的梁、墩及主塔都采用梁单元进行模拟，而斜拉索则采用桁架单元进行模拟。实桥模型共划分为240个单元、286个节点。斜拉桥实体模型如图2所示。

有限元计算过程中斜拉索的初始张拉力取值为5 600 kN，而弹性模量则根据钢绞线的实际弹性模量进行取值，考虑到防腐材料重量对斜拉索的影响，模型中斜拉索的容重按增加10%取值。模型中梁墩节点间刚接，梁塔节点间固结。计算荷载考虑恒载、温载、挂篮与湿重荷载、活载及混凝土的收缩徐变等。钢绞线与预应力钢筋参数取值如表1所示。

3 结果与分析

矮塔斜拉桥的主要设计参数包括主梁刚度比、边中跨比、边跨无索区长度等，本文将上述参数作为控制变量，探讨不同设计参数对矮塔斜拉桥受力及变形的影响规律。

3.1 主梁刚度比

通过建立主梁刚度比分别为0.2、0.6、1.0、1.4及1.8的矮塔斜拉桥模型，针对不同主梁刚度比的主梁边、中跨挠度及弯矩进行计算，得到最大挠度及弯矩变化曲线如图3所示。

根据图3（a）可知，随着矮塔斜拉桥主梁刚度比的增大，主梁边、中跨的最大挠度均呈不断减小的趋势变化，说明主梁刚度比对矮塔斜拉桥变形的影响显著。当主梁刚度比由0.2增至1.8时，主梁边跨最大挠度由158 mm减小至56 mm，减幅达64.5%，而主梁中跨最大挠度由232 mm减小至85 mm，减幅达63.3%，说明增大主梁刚度比可以大幅度降低矮塔斜拉桥主梁边、中跨变形量。由图3（b）可知，随着矮塔斜拉桥主梁刚度比的增大，主梁边、中跨的最大弯矩均呈不断增大趋势变化，说明主梁刚度比对矮塔斜拉桥受力存在影响。当主梁刚度比由0.2增至1.8时，主梁边跨最大弯矩由33 308 kN·m增至39 528 kN·m，增幅为18.7%，而主梁中跨最大弯矩由46 552 kN·m增至101 183 kN·m，增幅达117.3%，说明增大主梁刚度比会大幅度增加矮塔斜拉桥主梁中跨受力，不利于结构安全性。

3.2 边中跨比

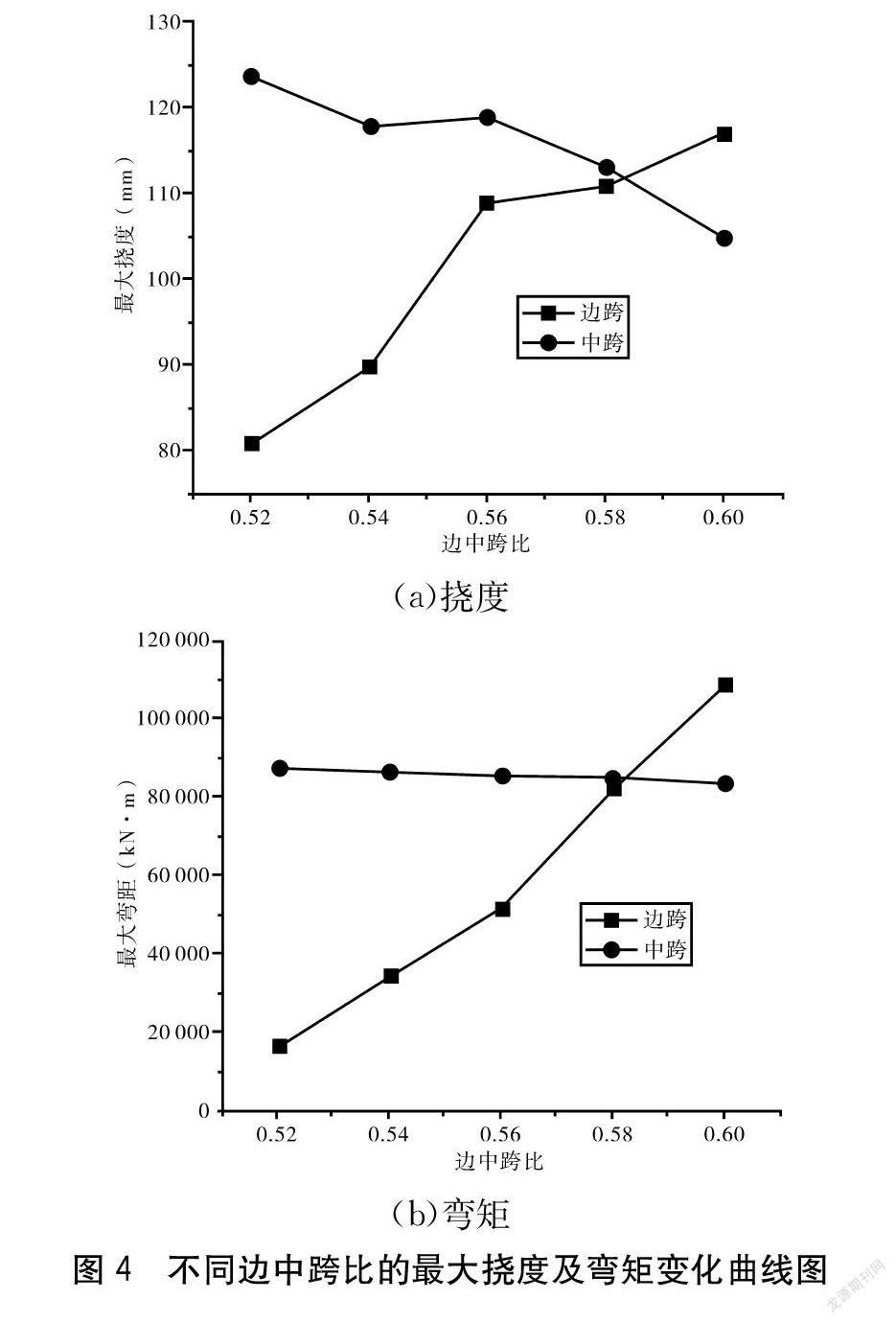
为研究边中跨比对矮塔斜拉桥受力及变形的影响，选取边中跨比分别为0.52、0.54、0.56、0.58及0.6，针对不同边中跨比的斜拉桥有限元模型进行受力及变形分析，得到最大挠度与弯矩计算结果如图4所示。

由图4（a）可知，矮塔斜拉桥主梁边跨的最大挠度随着边中跨比的增大呈逐渐增大变化趋势，而中跨的最大挠度则随之呈减小变化，表明矮塔斜拉桥的结构变形受边中跨比的影响较大。在边中跨比为0.52时，主梁边跨的最大挠度为82 mm，当边中跨比增至0.6时，边跨最大挠度达118 mm，增幅为43.9%;在边中跨比为0.52时，主梁中跨的最大挠度为125 mm，当边中跨比增至0.6时，中跨最大挠度减至106 mm，减幅为15.2%，說明边中跨比的增大在一定程度可以减小主梁中跨变形，但同时也导致边跨的变形大幅增加。根据图4（b）可知，斜拉桥主梁边跨的最大弯矩随着边中跨比的增大呈逐渐增大的变化趋势，而中跨的最大弯矩则随之呈缓慢减小变化，表明边中跨比在一定程度上对斜拉桥的结构受力存在影响。在边中跨比为0.52时，主梁边跨的最大弯矩为16 850 kN·m，当边中跨比增至0.6时，边跨最大弯矩达108 887 kN·m，增幅为546%;在边中跨比为0.52时，主梁中跨的最大弯矩为87 528 kN·m，当边中跨比增至0.6时，中跨最大弯矩减至83 999 kN·m，减幅仅为4%，说明边中跨比的增大会导致斜拉桥的主梁边跨受力增加，不利于桥梁结构安全。

3.3 边跨无索区长度

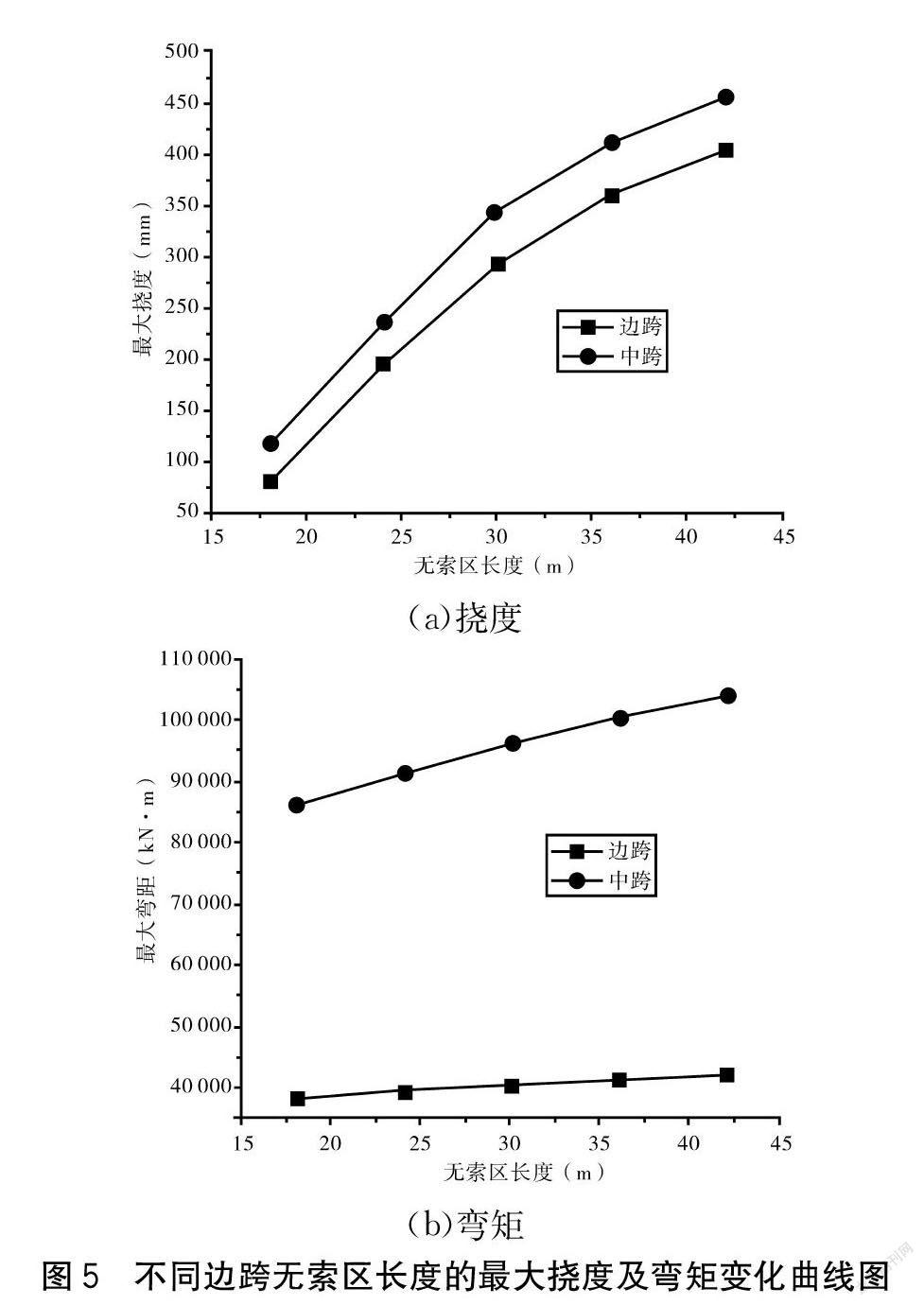
通过建立无索区长度分别为18 m、24 m、30 m、36 m及42 m的矮塔斜拉桥有限元模型，针对不同无索区长度的桥梁边、中跨挠度及弯矩进行计算，得到最大挠度及弯矩变化曲线如图5所示。

根据图5（a）可知，矮塔斜拉桥边、中跨最大挠度均随着边跨无索区长度的增大而不断增大，说明边跨无索区长度对矮塔斜拉桥变形的影响较大。当无索区长度由18 m增至42 m时，主梁边跨最大挠度由82 mm增至405 mm，增幅为394%，而中跨最大挠度由118 mm增至457 mm，增幅为287%，说明增大无索区长度会大幅度提升主梁边、中跨的变形量。由图5（b）可知，随着矮塔斜拉桥边跨无索区长度的增大，主梁边、中跨最大弯矩均呈不断增大趋势变化，说明无索区长度对矮塔斜拉桥受力存在影响。当无索区长度由18 m增至42 m时，主梁边跨最大弯矩由38 412 kN·m增至42 278 kN·m，增幅为10.1%，而主梁中跨最大弯矩由86 568 kN·m增至104 257 kN·m，增幅为20.4%，说明增大边跨无索区长度会在一定程度上增大矮塔斜拉桥整体结构受力。

4 结语

本文以某矮塔斜拉桥为研究背景，分别研究了不同主梁刚度比、边中跨比、无索区长度对主梁受力及变形的影响规律，得到以下结论：

（1）随着主梁刚度比的增大，矮塔斜拉桥主梁中跨、边跨的最大挠度均逐渐减小，而主梁中跨、边跨的最大弯矩逐渐增大，且主梁边跨弯矩增幅较小。

（2）矮塔斜拉桥主梁边跨的最大挠度随着边中跨比的增大逐渐增大，而中跨的最大挠度则逐渐减小;斜拉桥主梁边跨的最大弯矩随着边中跨比的增大逐渐增大，而中跨的最大弯矩则随之缓慢减小。

（3）随着边跨无索区长度的增大，矮塔斜拉桥边、中跨最大挠度均逐渐增大;随着边跨无索区长度的增大，斜拉桥主梁边、中跨最大弯矩均呈不断增大变化，但边跨弯矩增长幅度较小。

参考文献：

[1]申 磊，胡 锋，崔文涛.某大跨径双塔单索面矮塔斜拉桥动载试验研究[J].公路，2021，66（2）：124-128.

[2]杨德厚，邓同生，李顺波.矮塔斜拉桥塔梁同步施工阶段塔梁墩固结部位局部应力分析[J].交通科技，2021（2）：28-33.

[3]曹发源.矮塔斜拉桥塔跨比的优化研究[J].北方交通，2020（4）：34-37.

[4]李红豫，李 恒，吴 悦，等.基于BIM的东洲湘江大桥参数化设计应用研究[J].公路，2020，65（11）：173-178.

[5]鲍英基，蒋斌松，李文斌.PC矮塔斜拉桥运营阶段参数敏感性分析[J].公路，2020，65（8）：216-222.

[6]牛伟迪.异型钢结构单塔宽幅箱梁斜拉桥设计分析[J].中国市政工程，2021（2）：22-25，123.

[7]卫康华，罗 浩，杨孟刚.塔墩梁固结的三塔四跨矮塔斜拉桥成桥状态力学参数研究[J].铁道科学与工程学报，2017，14（5）：988-996.

[8]李德旭，乔文靖，彭晶蓉.斜拉桥主塔横梁设计参数对结构静力性能的影响[J].中国公路，2020（3）：100-101.

3783501908275