基于ANSYS-PDS的含缺陷压力容器可靠性分析*

周 娇，彭星煜，曹军峰，张杰东，刘金玲，姜 雪

(1.中石化安全工程研究院有限公司，山东 青岛 266000；2.西南石油大学 石油与天然气工程学院，四川 成都 610500；3.中石油青海油田分公司监督监理公司，甘肃 酒泉 736200)

0 引言

我国天然气压力容器在役时间较长，含缺陷天然气压力容器比例不断升高[1]。对已有的含缺陷天然气压力容器可靠性分析，API 581为现阶段压力容器可靠性分析的基础，而蒙特卡洛大范围抽样与模糊算法为其常用分析方法。李铁均等[2]采用人工神经网络方法探究了具有腐蚀和弯曲损伤的不完整管道结构的可靠性;张镇等[3]建立了基于贝叶斯方法的输油管道可靠性评估数学模型;魏同锋等[4]通过蒙特卡洛随机抽样对大范围数据进行概率分析，探究腐蚀管道的可靠性指标;向彦楠[5]基于故障树理论计算了故障树的最小割集，分析了集气站故障的主要影响因素;白路遥等[6]采用蒙特卡洛法计算了管段的失效概率值并进行了参数的敏感性分析，但单纯使用蒙特卡洛法工作量巨大;吴云冬[7]采用修正的API 581理论计算高含硫天然气集输站场设备的可靠性，将部分API 581的局限性进行了改进;王鹤男[8]采用进一步修正的API 581理论分析站场压力容器的可靠性。然而，蒙特卡洛随机抽样精度受抽样范围限制，精度越高，范围越大，模糊算法则在计算时主观性较强，精确度受限。 API 581分析数据来源受跨行业限制，针对压力容器部分的同类失效概率大多数来源于当时国外的炼油厂，压力容器种类相差较大，且API 581的分析数据较为老旧，因此，API 581对于我国天然气压力容器的适用性逐渐下降[9]。基于以上情况，开发1种新的方法来进行含缺陷天然气压力容器的可靠性分析迫在眉睫。因此，本文将常用于机械工程领域的ANSYS-PDS模块进行跨领域应用，基于压力容器现实数据通过建模分析含缺陷天然气压力容器的可靠性，从数据本质上克服API 581分析的局限性，对于实现含缺陷天然气压力容器安全生产运行与运维管理具有重要意义。

1 研究方法

基于API 581分析压力容器可靠性的局限性，本文基于“应力-强度”干涉理论将压力容器的内径、原始壁厚、缺陷深度、压力容器内压设置为服从正态分布的随机变量，基于响应面法结合蒙特卡洛抽样分析，通过撰写APDL代码，在ANSYS软件的PDS模块中分析压力容器的可靠性，下文阐述“应力-强度”干涉理论与响应面法基本原理。

1.1 “应力-强度”干涉理论

量化可靠性的指标较多，本文采用失效概率指标来量化含缺陷天然气压力容器的可靠性。失效概率Pf是指压力容器在一定的失效机理和破坏状态下发生失效的概率[10]。本文基于“应力-强度”干涉理论来计算破坏失效状态模式下的失效概率Pf。

在含缺陷天然气压力容器可靠性分析中，假设压力容器的功能函数Z=R-S，如式(1)所示[11]。

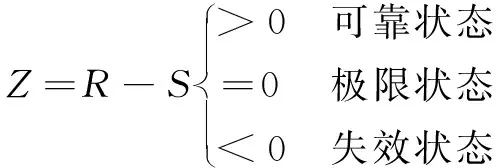
(1)

式中：Z为压力容器现处于的状态；S为压力容器所受载荷；R表示压力容器承受“载荷”的能力，称为抗力。因此，当外力作用在压力容器上引起的“载荷”达到、等于或大于压力容器的抗力时，就达到了压力容器可靠性的极限状态，会导致压力容器失效。

载荷、抗力的概率分布曲线如图1所示，2条曲线在随机变量影响下可能相交，其重叠部分称为干涉区，如图1(c)中阴影区域所示。即压力容器可能出现的失效区域[12]。

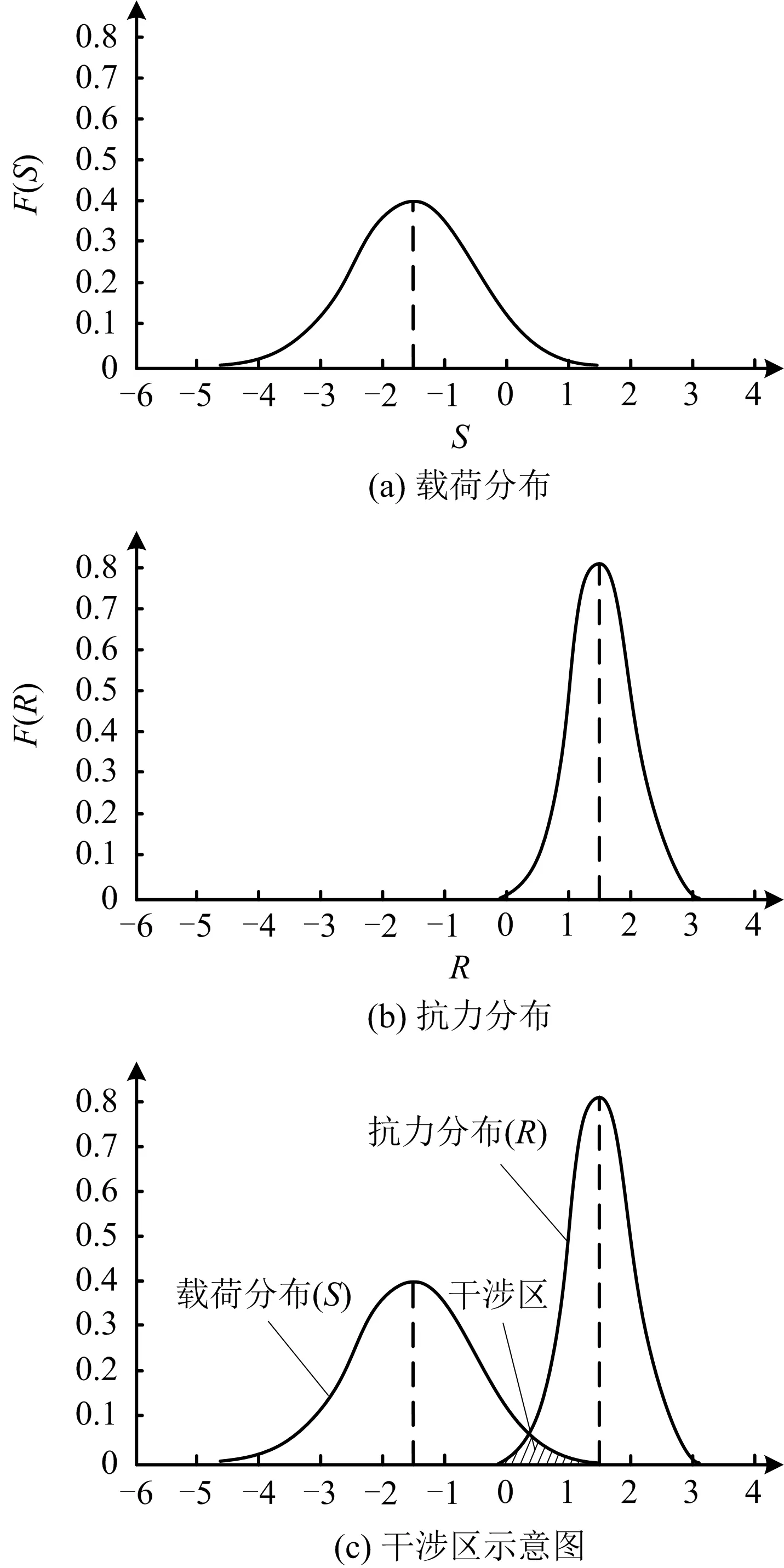
图1 载荷与抗力分布示意Fig.1 Schematic diagram of load and resistance distribution

假设含缺陷天然气压力容器的失效取决于若干随机变量Xi(i=1,2,…,n)，如压力容器内压、缺陷深度等。计算这些基本变量的1个很好的方法就是计算可靠性概率[13]。若已知基本变量Xi(i=1,2,…,n)的联合分布密度函数f(X1,X2,…,Xn)，则压力容器的失效概率如式(2)：

(2)

1.2 响应面法基本原理

采用ANSYS软件中PROB DESIGN模块，基于响应面法(Response surface method,RSM)进行分析，编写APDL命令流，修改参数即可改变模型，可以最终计算出静压力容器的失效概率。计算出随机变量的不确定性导致的压力容器失效概率；通过灵敏度分析确定随机变量对失效概率的影响程度。

响应面法的基本原理是通过一系列确定性实验拟合1个响应面来模拟真实的极限状态曲面，从而进行可靠性分析。其中，模拟分析过程中的循环次数由随机变量的个数确定，因此，需选择对输出结果有重大影响的变量作为随机变量。

1.2.1 一次响应面法

鼓励学生积极将实训课题与院系的创新科研相结合，利用现有条件在完成实训作业的同时参加各项物联网工程的相关专业比赛，如各级机器人大赛，蓝桥杯、ACM等程序设计比赛。培养学生的创新思维、动手实践能力与团队协作能力。

设含有2个基本变量X1，X2的极限状态函数为Y=g(X1,X2),它一般是非线性的，这一方法的几何表示如图2所示。取响应面函数为一次多项式，如式(3)：

Y′=g′(X1,X2)=a0+a1X1+a2X2

(3)

式中：a0，a1，a2是待定系数。

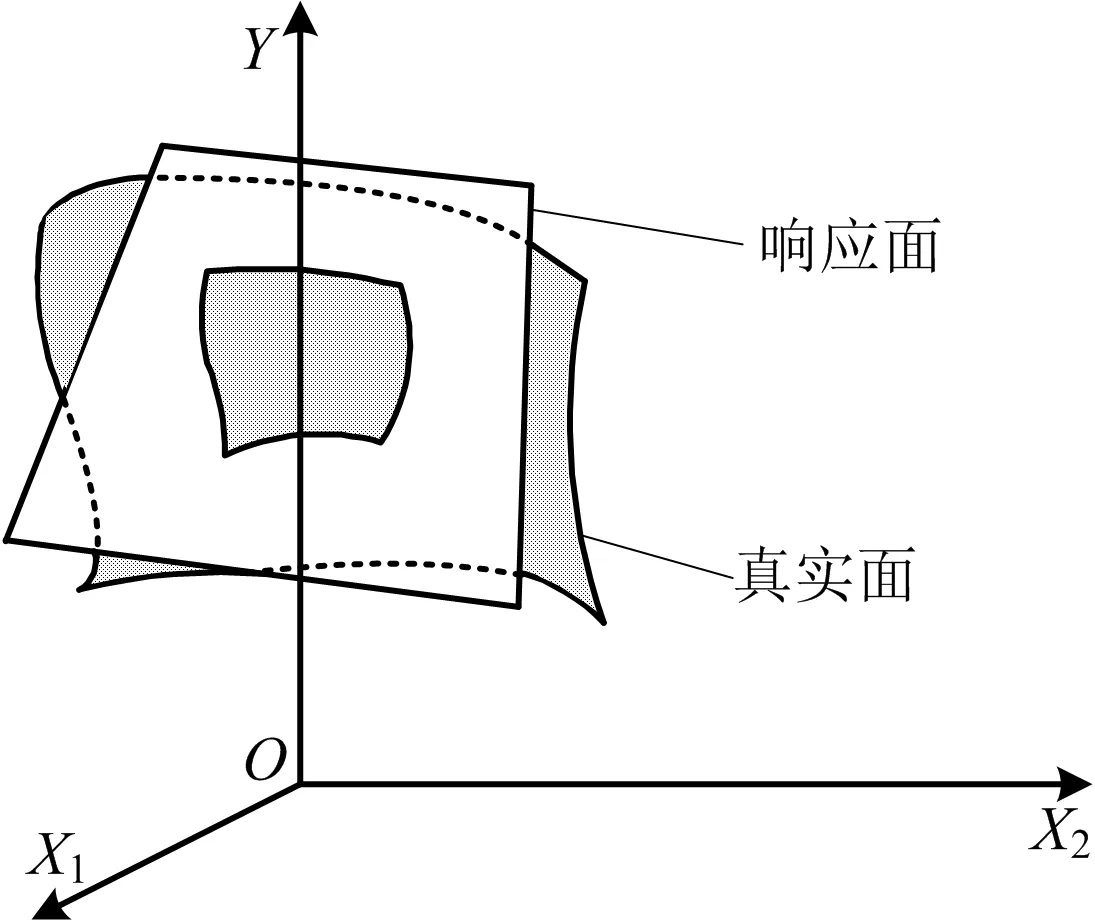
图2 变量X1,X2的线性响应面Fig.2 Linear response surface of variables X1,X2

1.2.2 二次响应面法

二次响应面法采用二次多项式形式，如式(4)：

(4)

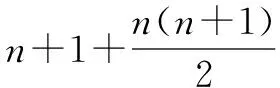
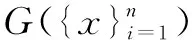
2 基于响应面法的压力容器可靠性分析

以某在役天然气集输站内压力容器污水罐-1为例，进行基于ANSYS-PDS的压力容器失效概率分析。该污水罐的最大设计压力为1.6 MPa，操作压力为0.1 MPa，最大设计温度为40 ℃，操作温度为20 ℃，设备长度5.8 m，压力容器材料为20 R钢，屈服强度245 MPa，泊松比0.28，弹性模量206 GPa。

2.1 计算模型

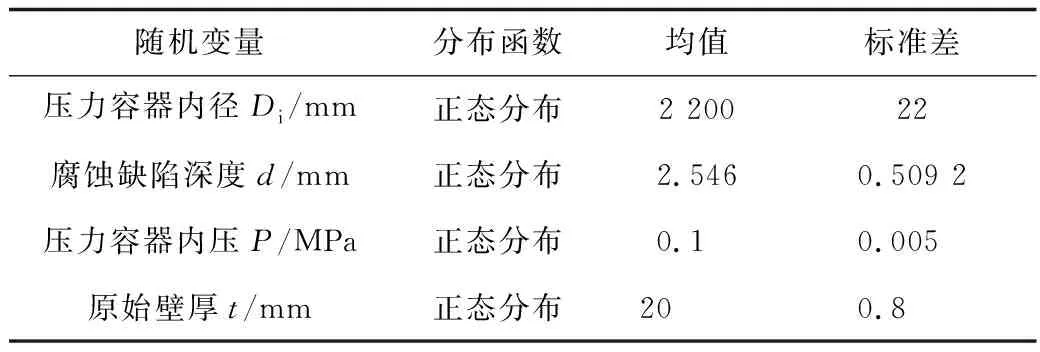
表1 随机变量参数Table 1 Parameters of random variables

图3 压力容器模型与网格划分Fig.3 Model and mesh generation of pressure vessel

对压力容器而言，如钢材参数之类变异性较小的随机变量对结构可靠度的影响微乎其微，如果对所有参数都按随机变量处理，不仅会导致模拟效率的低下，还不一定能起到提高精度的效果。因此，忽略压力容器同种钢材之间的微小变化，比如屈服强度等参数，主要对压力容器失效概率影响较大的变量参数考虑其随机性，将其设置成随机变量，根据挪威船级社(DNV) ORBIT-Onshore软件的HELP文档中给出的标准差计算方法进行取值。由应力-强度干涉模型可知，4个随机变量服从正态分布，缺陷处采用局部加密网格，缺陷尺寸(长×宽)变量取值为现场检测最大数据5 mm×5 mm，角度变量取值为6点钟方向(顺时针依次为1～12点钟方向)。

2.2 边界条件

从现场压力容器安装条件可知，考虑其内压与自重。由于压力容器为封闭模型，在模型的下表面边界均采用了沿相应法线方向上的零位移约束，认为不允许其产生法线方向的移动。

2.3 失效准则

在腐蚀坑腐蚀减薄模式下，失效的应力为压力容器在其筒体上所受到的最大应力，则压力容器的结构功能函数如式(5)所示，当y>0时，压力容器失效。

y=σm-σs

(5)

式中：σm为压力容器所受最大应力，ANSYS计算得出mises应力，MPa；σs为压力容器材料屈服强度，MPa。

根据失效准则，由ANSYS计算确定压力容器整体结构中应力最大的单元，以此为中心搜寻可靠度小于工程要求的单元，计算压力容器整体失效概率。

2.4 响应面设置

根据响应面类型以及响应面中输出变量的转换函数，应选择1种误差最小的响应面设置类型进行响应面的拟合，即进行响应面的优选。

用于评估响应面的回归模型主要有2种，即线性与二次，也就是一次响应面与二次响应面。在二次响应面中又分为全二次项(有交叉项)二次响应面与纯二次项(无交叉项)二次响应面，因此，响应面种类主要有3种：线性(LIN)，全二次项(QUAX)与纯二次项(QUAD)。

对于转换函数(Y-trans)，是应用于输出参数的转换类型的选项，主要用于优化拟合过程，转换函数主要有8种，见表2。

表2 响应面类型Table 2 Types of response surface

对不同响应面类型进行逐一计算以优选最佳响应面拟合方式，如表3所示。根据计算误差可知，最佳响应面拟合方式为采用全二次项(QUAX)响应面，转移函数采用SQRT类型。最终ANSYS-PDS拟合的对于所有随机变量的响应面如图4所示。

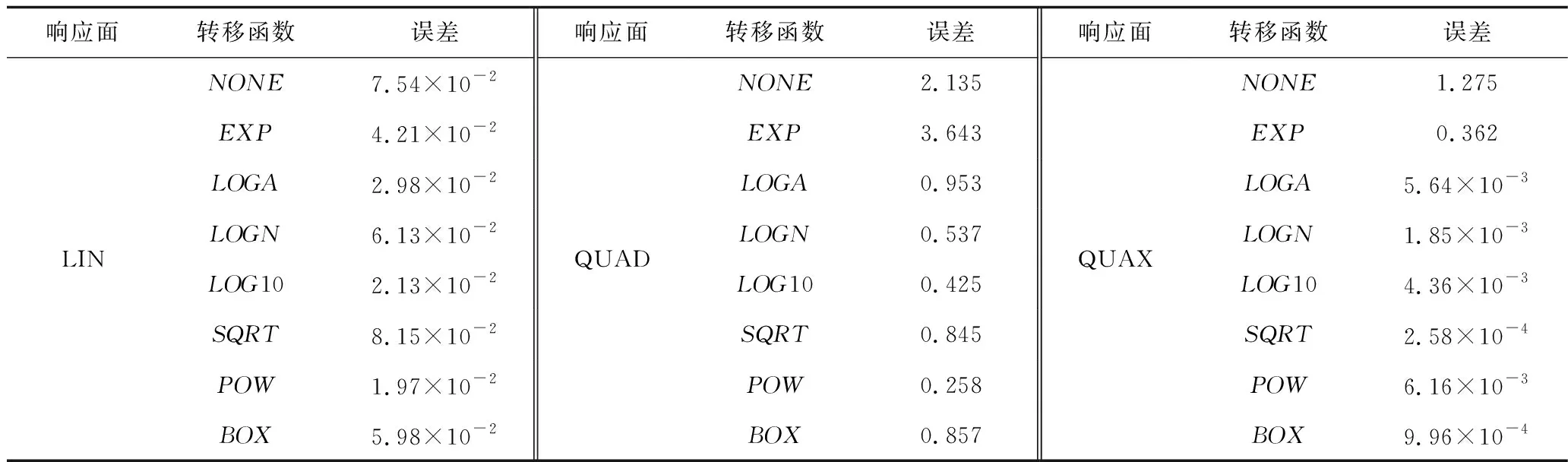
表3 不同响应面类型误差Table 3 Errors of different types of response surface

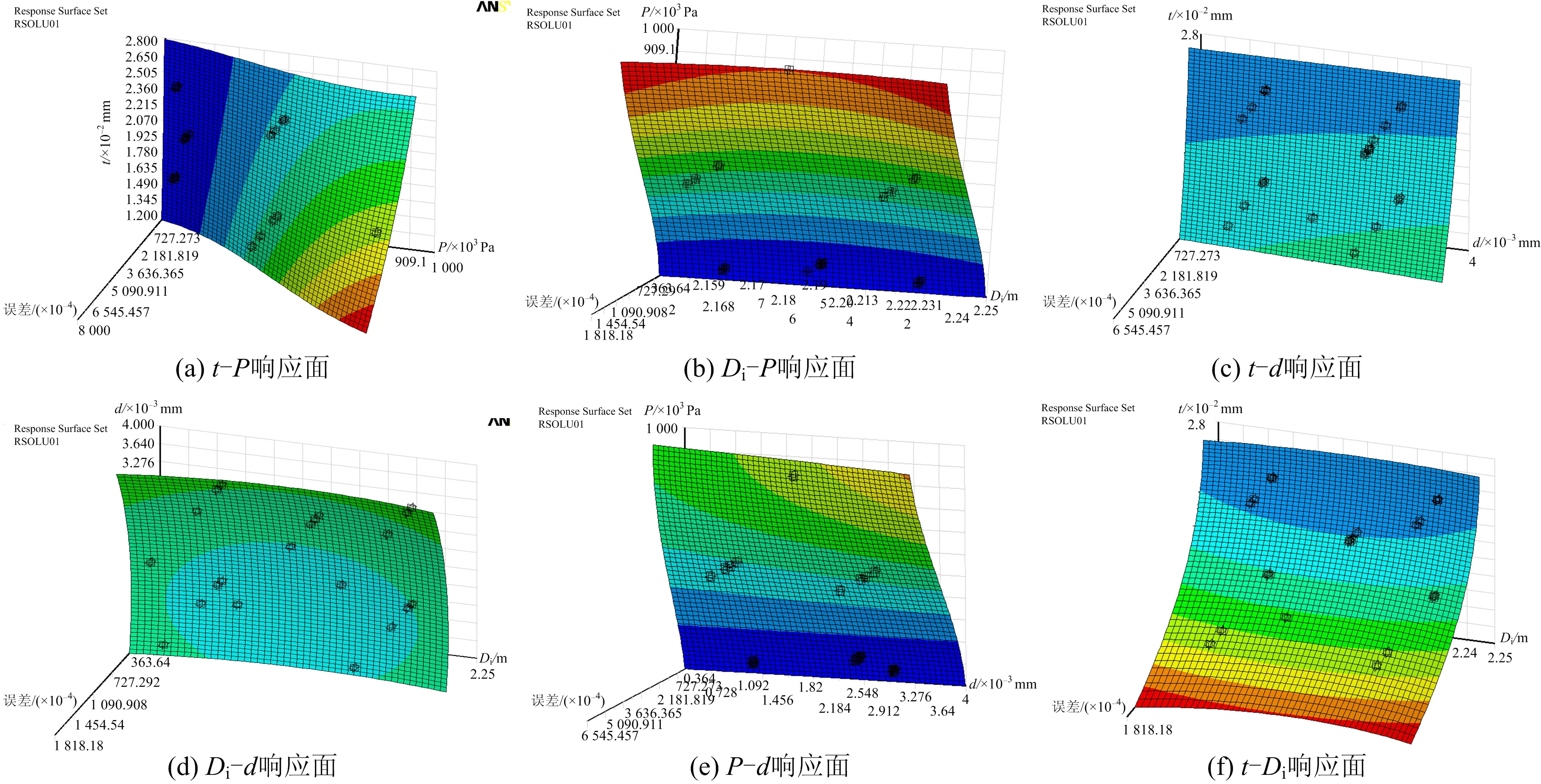
图4 随机变量的拟合响应面Fig.4 Fitting response surface of random variables

2.5 失效概率分析

基于响应面法，结合蒙特卡罗方法抽样提高失效概率的计算效率，对蒙特拉洛抽样次数进行优选，分别选取100次～10万次不等抽样次数进行优选，如图5所示。根据抽样曲线可得出，10万次抽样已趋近于数据平稳状态，因此，选择10万次的蒙特卡洛抽样进行响应面的计算。根据失效准则确定应力最大的单元，以此为基础计算压力容器的失效概率。对于ANSYS-PDS 4个随机变量的蒙特卡洛抽样取值如图6所示。最终ANSYS-PDS计算出的压力容器失效概率计算结果以及随机变量对于压力容器的灵敏度分析结果如图7所示。

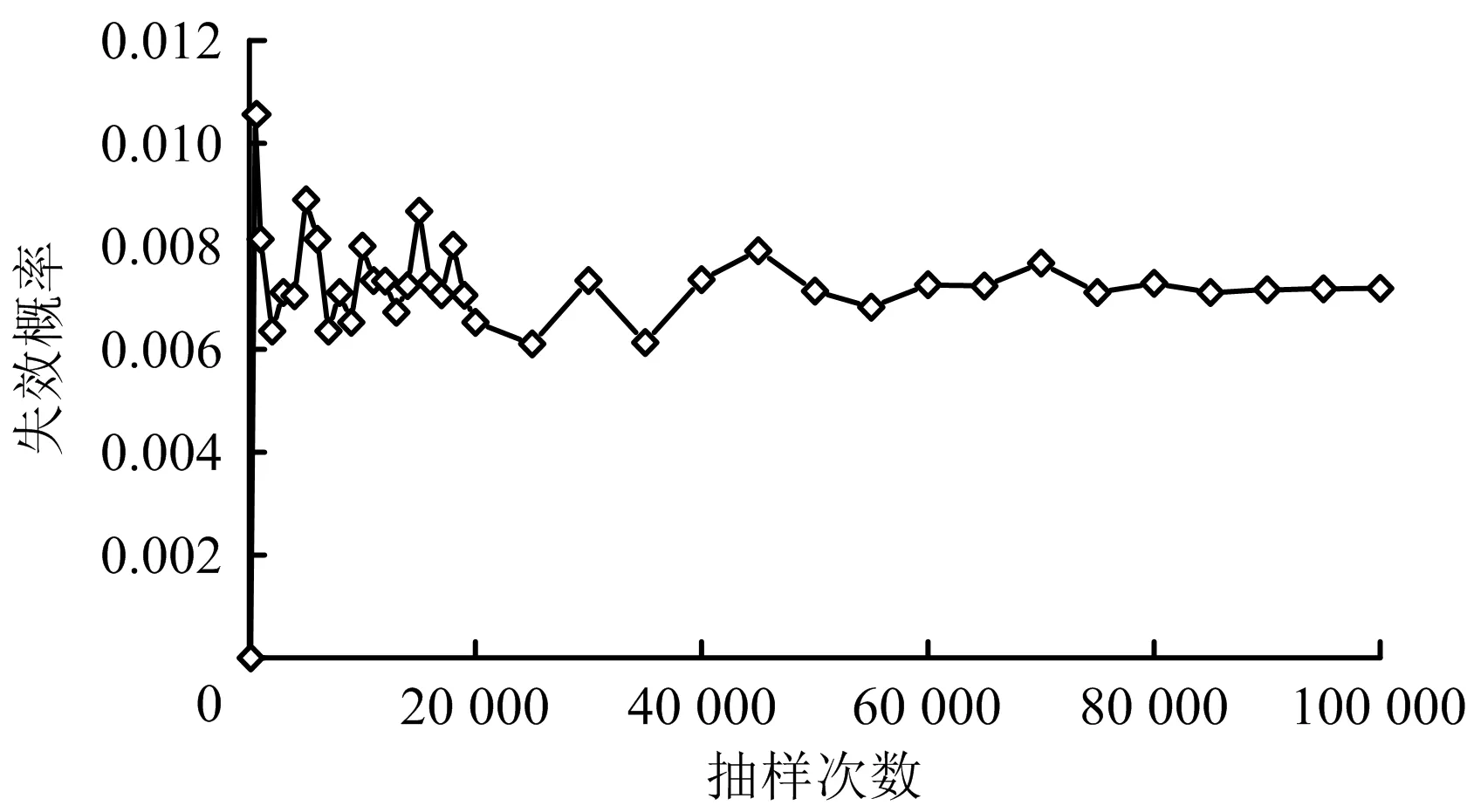
图5 蒙特拉洛抽样次数优化曲线Fig.5 Optimization curve of Monte Carlo sampling times

图7 压力容器失效概率计算结果以及灵敏度分析结果Fig.7 Calculation results of failure probability and sensitivity analysis results of pressure vessel

根据以上计算结果可知，压力容器污水罐-1的失效概率为7.201×10-3，则该压力容器的可靠度为0.992 799。

通过ANSYS导出的压力容器失效概率对各随机参数的灵敏度分析可知，4个随机变量对该压力容器可靠性的影响程度及大小排序为：原始壁厚(59.43%)>压力容器内压(20.20%)>缺陷深度(17.96%)>压力容器内径(2.40%)。明显看出，对于该压力容器，其原始壁厚对于压力容器失效概率的影响相较其他随机变量影响最大，且为负影响，即在其他同等条件下，压力容器原始壁厚越大，含缺陷天然气压力容器的失效概率越小。对于该压力容器内压、缺陷深度随机变量，二者影响程度相差不大，均处于随机变量原始壁厚之后，对于失效概率也均为正影响。因此，对于该含缺陷天然气压力容器的运行管理，应重点关注其运行压力与缺陷深度的变化，将其控制在合理范围内，保障其安全平稳运行。对于压力容器原始内径，其为正影响，影响程度也较小。灵敏度分析对实现含缺陷天然气压力容器安全生产运行管理具有重要意义，也可为其它类似压力容器的可靠性分析提供参考和借鉴。

3 结论

1)采用ANSYS软件中的PDS模块建模求解分析含缺陷天然气压力容器的可靠性，从本质上克服了API 581分析的局限性，为天然气压力容器的可靠性分析带来了1种新的方法，其分析过程采用压力容器本身数据，比API 581更贴近压力容器现实工艺状态，可得到较为准确的可靠性分析结果。

2)将压力容器的内径、原始壁厚、缺陷深度、压力容器内压设置为随机变量，由应力-强度干涉模型可得随机变量均服从正态分布，基于响应面法结合蒙特卡洛法抽样分析，通过编写APDL代码，对实例中的含缺陷天然气压力容器进行可靠性分析，计算出该压力容器的失效概率为7.201×10-3，相应的，该压力容器的可靠度为0.992 799。

3)通过敏感性分析可知，4个随机变量对该压力容器可靠性的影响程度及大小排序为：原始壁厚(59.43%)>压力容器内压(20.20%)>缺陷深度(17.96%)>压力容器内径(2.40%)。这对实现含缺陷天然气压力容器安全生产运行管理具有重要意义，可为其他类似压力容器的可靠性分析提供参考和借鉴。