基于有上下界风量约束的矿井风量极值流算法研究*

尚文天，邓立军，刘 剑

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛125105;2.辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛125105)

0 引言

在矿井通风系统中，井巷风速过高不仅会引起粉尘飞扬，危害作业人员健康，增加粉尘爆炸的可能性，同时使通风阻力和矿井漏风率加大，导致风机耗电量增加，极大地增加了通风成本[1-2]。而当风速过低时又会无法满足工作地点通风量需求，及时稀释、排出有害气体等，甚至还可能导致瓦斯积聚，引起瓦斯爆炸和火灾事故[3]。《煤矿安全规程》对于不同类型井巷的风速上限与下限作出了明确规定[4]。因此，矿井的总风量也存在上限与下限，该上限为最大通风量，下限为最小配风量。

全矿最小配风量与最大通风量是矿井设计与生产系统改造的重要参数[4]。当最小配风量与最大通风量比较接近时，说明该通风系统的设计比较经济，但扩大生产的潜力小；当最小配风量与最大通风量相差较大时，说明该通风系统有较大的改造潜力[5]。但是在实际矿井通风设计中，矿井总需风量只是简单地将各用风地点需风量线性求和，按照“由里至外”原则分配各巷道风量。这一方法仍存在着工作面供风量不能满足需风量要求的问题[6]，并且部分巷道的风速可能无法满足《煤矿安全规程》对巷道最低风速的要求。

国内外学者针对最大流算法的研究已经比较成熟，一类是增广路径算法，另一类是预流推进算法[7]。很多学者也提出了其他改进算法，江锦成等提出的SAPR算法是在预流推进算法的基础上提出的自适应算法，具有很强的适应性和稳定性，为高效求解网络最大流的研究提供了一种新思路[8]；赵礼峰等提出了1种增广链修复算法，该算法能够计算更大规模的网络，并高效地处理一类稀疏网络[9]；刘剑等提出的利用找独立通路的思想来找增广路在程序思想的简洁性与运算量上都远优于经典算法[10]；罗甜甜等提出了在最短增广链算法基础上根据相应规则来选取增广链的算法，可以保证最短增广链优先选取，增加了算法的准确性与高效性[11]；杜政均针对大规模网络提出了Sense-Push算法，是1种最大流并行化算法，极大地提高了数据处理效率[12]。但是，采用最大流算法求最大通风量只考虑井巷的最高风速作为分支容量上界，忽略了井巷的最低风速限制，最终得到的最大总通风量无法保证所有巷道都满足《煤矿安全规程》规定的最低风速。而关于矿井最小配风量的计算，仍未存在正确有效的算法。

本文针对矿井通风系统的最大通风量和最小配风量问题，提出1种基于有上下界风量约束的极值流算法。即采用图论数学方法，先将矿井的巷道和交叉口抽象为有向图网络模型，依据《煤矿安全规程》与《煤矿通风能力核定标准》[13]，确定分支风量上界与风量下界约束，将求矿井最大通风量、最小配风量问题转换为有上下界风量约束的最大流和最小流问题并进行求解。

1 井巷最大、最小风量约束

井巷最大、最小风量约束要综合考虑《煤矿安全规程》第101条与第110条规定的井巷最高风速、最低风速以及各用风地点实际需风量等因素。最大风量约束由井巷最高风速来确定，最小风量约束则取井巷最低风速、各用风地点实际需风量的最大值[14]。

《煤矿通风能力核定标准》AQ 1056—2008对各用风地点需风量的计算方法作出了相关规定，以采煤工作面为例，计算出采煤工作面的最大、最小风量约束。取上述计算风量中最大者作为采煤工作面的最小风量约束，如式(1)所示：

qcfmin=max {qcf1,qcf2,qcf3,qcf4,qcf5,qcf6}

(1)

式中：qcfmin为采煤工作面的最小风量，m3/min；qcf1为按采煤工作面气象情况计算得出的最小风量，m3/min；qcf2为按采煤工作面的瓦斯涌出量取采煤工作面不均衡通风系数最小值计算得出的最小风量，m3/min；qcf3为按采煤工作面二氧化碳涌出量计算得出的最小风量，m3/min；qcf4为按炸药量计算得出的最小风量，m3/min；qcf5为按现场最多作业施工人数计算得出的最小风量，m3/min；qcf6为按风速进行验算得出的最小风量，m3/min。

最大风量约束由井巷的最高风速来确定。《煤矿通风能力核定标准》也作出了相关规定，仍以采煤工作平面为例列出相关计算公式，如式(2)所示：

qcfmax≤60×4.0×Scs

(2)

式中：qcfmax为按风速进行验算得出的采煤工作面的最大风量，m3/min；Scs为采煤工作面最小控顶有效断面积，m。

其他巷道及用风地点的最小风量、最大风量计算方法均可以此类推。

2 基于有上下界风量约束的极值流算法

基于文献[15]与[16]提出1种基于有上下界风量约束的极值流算法，弥补文献[5]求解最大流过程中忽略了分支容量下界与最小流计算方法，只适用于部分网络的缺陷，算法的具体流程如图1所示。

图1 基于有上下界风量约束的极值流算法流程Fig.1 Flow chart of extreme flow algorithm based on upper and lower bound air volume constraints

2.1 有源汇的有上下界流网络定义

与传统最大流问题的流网络定义不同，有上下界流网络中分支的流量不只是简单的大于等于0，而是大于等于某一个下界。单一源汇流网络G=(V,E)，其源汇点分别为s和t，E中的每条分支(u,v)都有容量下界b(u,v)≥0和容量上界c(u,v)≥0限制，且每条分支(u,v)给定1个流量值f(u,v)，如果f满足以下2个条件，则称f是G的1个可行流[15]。

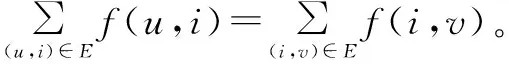
2)容量限制条件：E中的任意1条分支(u,v)都满足b(u,v)≤f(u,v)≤c(u,v)。

2.2 有上下界流网络的可行流

根据文献[15]，为求得可行流或者指出这样的可行流不存在，便要根据计算原流网络的无上下界等效流网络G′(V′,E′)的最大流进行判断。为解决等效流网络因不存在容量上下界而导致其不满足流量平衡与容量限制条件，保证等效流网络的最大流f′(u,v)与原流网络的可行流f(u,v)满足关系式(3)：

f(u,v)=f′(u,v)+b(u,v)

(3)

应对等效流网络G′作如下定义：

1)G′的节点集合V′除包含原流网络节点集合V中的所有节点外，再添加附加源点s′与附加汇点t′作为与不平衡节点相连分支的源汇点，即V′=V∪{s′,t′}。

2)G′的分支集合E′包含下列分支：

①原流网络分支集合E中的所有分支。这些分支的容量取c′(u,v)，即满足公式(4)：

c′(u,v)=c(u,v)-b(u,v)

(4)

②1条汇点t至源点s的新分支(t,s)，该分支容量设为+∞。

③为处理容量下界条件b(u,v)，根据下列方法遍历所有节点后建立的新分支。

用m(i)表示原流网络中任意节点i流入的下界总和减去流出的下界总和，即公式(5)：

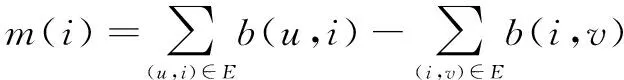
(5)

根据m(i)的不同，分支的建立方式也不同，具体方式如下：

A.当m(i)=0时，表示流入的下界总和等于流出的下界总和，节点处流量平衡，无需建立新分支。

B.当m(i)>0时，表示流入的下界总和大于流出的下界总和，故要将流入的多余流量m(i)用其他分支流入该节点。利用附加源点s′建立分支(s′,i)，其分支容量设为c′(s′,i)=m(i)。

C.当m(i)<0时，表示流入的下界总和小于流出的下界总和，故要将流出的多余流量m(i)用其他分支流出该节点。利用附加源点t′建立分支(i,t′)，其分支容量设为c′(i,t′)=-m(i)。

以上便是等效流网络的定义，其示意如图2所示。

图2 等效网络示意Fig.2 Equivalent network diagram

再通过已经成熟和完善的最大流算法[7]计算G′最大流f′，根据等效流网络的定义，其中与原流网络相同分支的f′(u,v)要满足无上下界的容量限制与流量平衡条件，故应符合公式(6)，(7)：

0≤f′(u,v)≤c′(u,v)

(6)

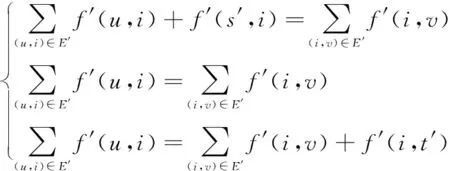
(7)

通过公式(3)，(4)，(6)可推出b(u,v)≤f(u,v)≤c(u,v)，即f(u,v)满足流量平衡条件。

故可根据附加源点s′流出或流入附加源点t′的分支是否都达到饱和进行判断，有以下2种情况：

1)附加源点s′流出或流入附加源点t′的分支都达到饱和，满足容量限制与流量平衡条件，原流网络G中存在可行流，即在G′最大流为f′时，根据公式(4)求得每条分支上的可行流f(u,v)。

2)附加源点s′流出或流入附加源点t′的分支未都达到饱和，只满足容量限制条件，原流网络G中不存在可行流。

存在可行流的情况下，等效流网络的分支(t,s)上的流量为原流网络可行流总流量的值。可行流满足并不是一定最小流、也不一定是最大流，只能保证每条分支的流量满足其容量上下界要求。

2.3 有上下界流网络的最大流

可行流流量一定在上下界中，但是可能存在可增加的流量，这些流量存在于每条分支容量上界大于可行流流量的部分中。故可通过建立残留网络，即将原流网络的分支容量改为容量上界与可行流流量的差，即残留容量。再求其最大流，得到的最大流为增广最大流，再将其与原流网络的可行流相加，即为原流网络的最大流即矿井的最大通风量。具体步骤如下：

1)建立残留网络G残(V,E)，用c残(u,v)表示残留网络分支容量，如式(8)所示：

c残(u,v)=c(u,v)-f′(u,v)

(8)

2)对残留网络G残进行1次最大流计算，计算得出其每条分支的增广最大流量为f残(u,v)。

3)计算原流网络G最大流的分支流量，用fmax(u,v)表示原流网络G处于最大流情况下分支(u,v)的流量值，如式(9)所示：

fmax(u,v)=f′(u,v)-f残(u,v)

(9)

4)计算原流网络G的最大流，用Fmax(G)表示原流网络G处于最大流情况下的总流量值，如式(10)所示：

(10)

2.4 有上下界容量限制下网络的最小流

可行流流量除可能存在可增加的流量外，也可能存在可减少的流量，这些流量存在于每条分支可行流流量大于容量下界的部分中。故可通过建立反转残留网络，即使原流网络分支反转，其分支容量改为可行流流量与容量下界的差，即反转残留容量。再对其求最大流，得到的最大流为消减最大流，再用原流网络的可行流减去消减最大流，即为原流网络的最小流即矿井的最小配风量。具体步骤为：

1)建立反转残留网络G反(V,E)，反转流网络G的流向，用c反(v,u)表示残留网络分支容量，如式(11)所示：

c反(v,u)=f′(u,v)-b(u,v)

(11)

2)对反残留网络G反进行1次最大流计算，计算得出其每条分支的消减最大流为f反(v,u)。

3)计算原流网络G最小流的分支流量，用fmin(u,v)表示原流网络G处于最小流情况下分支(u,v)的流量值，如式(12)所示：

fmin(u,v)=f′(u,v)-f反(v,u)

(12)

4)计算原流网络G的最小流，用Fmin(G)表示原流网络G处于最小流情况下的总流量值，如式(13)所示：

(13)

3 实例分析

3.1 可行流计算

以文献[5]中的通风网络为例，如图3所示，源点和汇点分别为V1和V10，分支的容量上、下界见表1。

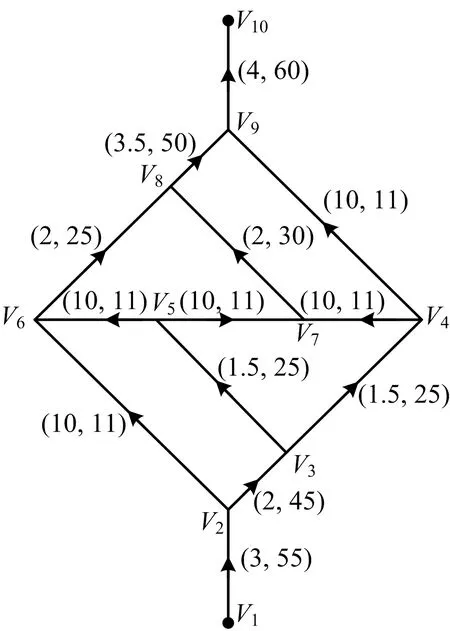
图3 13分支通风网络Fig.3 Thirteen edges ventilation network

表1 通风网络分支的容量上、下界Table 1 The upper and lower bounds of edges capacity inventilation network

先计算该通风网络的可行流，按照前文的方法添加1条由汇点t至源点s的新分支(t,s)，该分支容量设为无穷大+∞。等效流网络包含的原流网络分支的容量为原容量上界减去下界。构造等效流网络添加附加源s′和附加汇t′。根据任意节点i流入下界总和减去流出下界总和的值m(i)添加新分支(s′,i)或(i,t′)，所有节点的m(i)通过计算添加的分支及其容量、饱和状态见表2，可知所有从附加源点s′流出或流入附加汇点t′的分支均达到饱和，因此，原流网络存在可行流，可行流分配结果见表3。

表2 原流网络分支的容量下界Table 2 The lower bound of the capacity of the edges of the original stream network m3/s

表3 通风网络可行流分配结果Table 3 The feasible flow distribution results of the ventilation network

以上过程所建立的等效流网络与求解出的原流网络可行流风量分配结果如图4所示，可看出等效流网络与原流网络中任意节点的流入量与流出量保持等效。

图4 求解原流网络可行流风量分配Fig.4 Seeking the feasible flow air volume distribution of the original flow network

3.2 最大流计算

建立残留网络，即原流网络的分支容量改为容量上界与可行流的差c残(u,v)。残流网络所有分支的容量、最大流算法求解后的流量以及饱和状态见表4。将残留网络的最大流与原流网络可行流相加，即为原流网络的最大流。根据其源汇点的流出与流入值，可得通风网络最大流的流量值为55，即该矿井的最大通风量为55 m3/s。

表4 残留网络的分支容量Table 4 Edges capacities of residual network

以上过程所建立的残留网络与求解出的原网络最大流如图5所示，可以看出残留网络中源汇点之间存在通路，故可使用最大流方法对其求解，求解结果即为增广最大流。

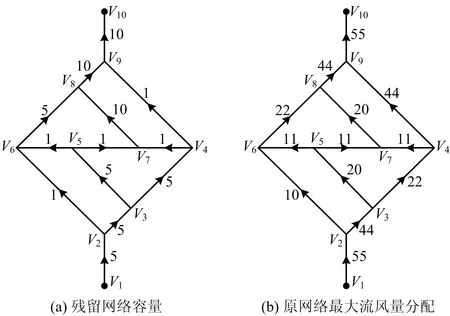
图5 求解原流网络最大流风量分配Fig.5 Seeking the distribution of maximum air flow in the original flow network

3.3 最小流计算

建立反转残留网络，即原流网络的分支容量改为可行流与容量下界的差c反(v,u)，并使原流网络分支反转。反转残流网络所有分支的容量、最大流算法求解后的流量以及饱和状态见表5。根据其源汇点的流出与流入值，可得通风网络最小流的流量值为50，即该矿井的最小配风量为50 m3/s。

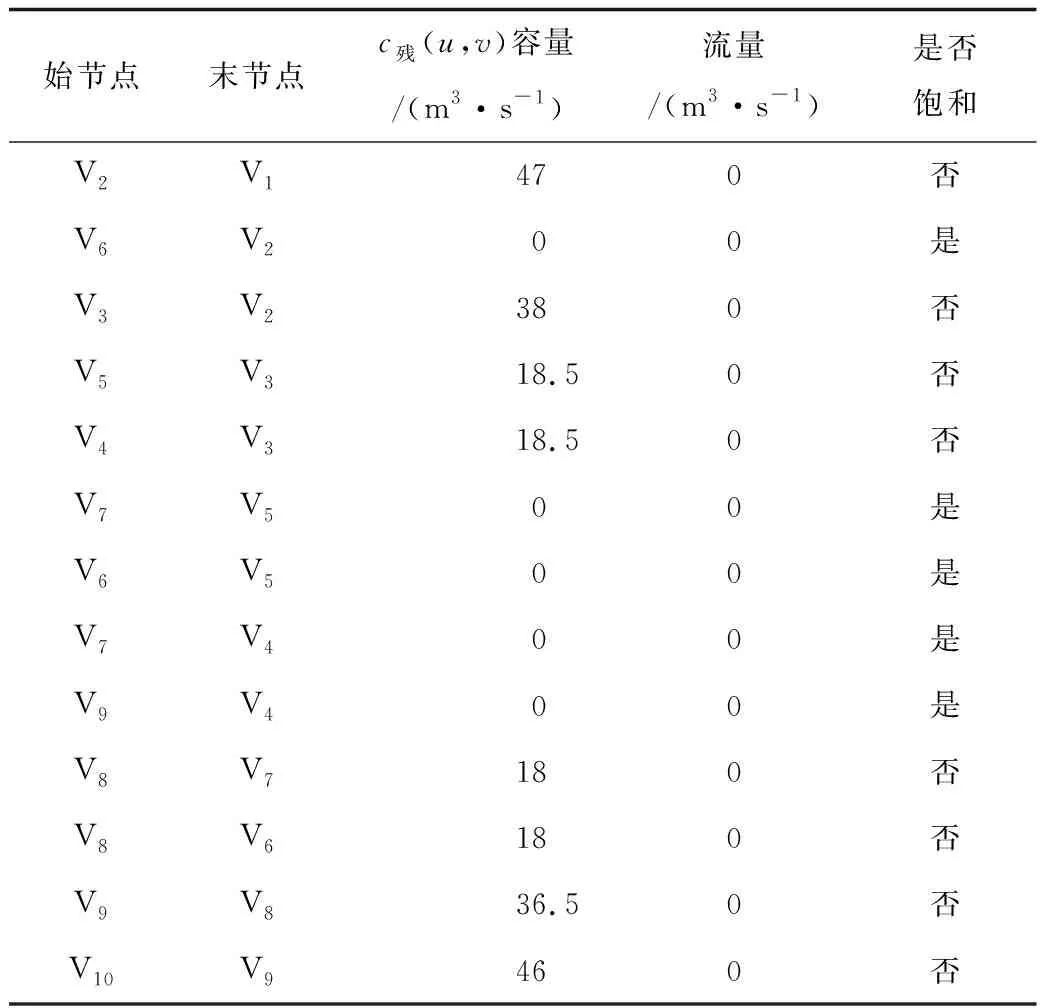
表5 反转残留网络的分支容量Table 5 Edges capacities of reversal residual network

以上过程所建立的反转残留网络与求解出的原网络最小流见图6，可看出反转残留网络中源汇点之间无通路，故其最大流量一定为0，故不存在消减最大流。

图6 求解原流网络最小流风量分配Fig.6 Seeking the distribution of minimum air flow in the original flow network

4 结论

1)提出的基于有上、下界风量约束的矿井风量极值流算法，改进了文献[5]分支分配到的流量不一定在上、下界约束内、最小流的计算方法应用范围小的弊病。不仅可以计算出流网络的极值流，还可以求出其中每个分支的流量分配情况。并且通过增加分支容量上、下界约束，使求得的极值流满足所有分支分配到的流量都在容量的上、下界约束内。

2)通过实例验证，本文提出的计算方法在满足上、下界限制的可行流基础上通过分别向容量上、下界逼近得出最大流与最小流，故可保证求得的最大流与最小流都同时满足上、下界限制。

3)基于有上、下界风量约束的极值流算法可应用于矿井通风系统，准确地求解出矿井通风系统的最大、最小通风量，并给出分配方案，在保证安全的前提下，减少开支，增大收益。还可以使用本算法评定矿井通风系统的经济性与矿井改造潜力，为矿井改造方案提供依据。本算法除应用于矿井通风系统外，还可以应用其他需要上、下界容量限制的流体网络，如电路分支上有用电元件的电路网络等。