设备租赁企业的预防性维修人员配置研究
刘文茜 金玉兰



摘 要:為了节约维修成本和设备的维修时间,建立了多台设备预防性维修的人员配置和维修成本优化模型。将总预防性维修成本作为优化目标,同时综合考虑了出租方的超承诺期维修任务量与维修人员数量的协调,以及超承诺期的维修惩罚,用MATLAB仿真求解出模型的最优人员配置和总预防性维修成本。并通过实例表明,考虑设备预防性维修人员配置和预防性维修的超承诺期任务量惩罚成本使设备预防性维护的更符合实际情况,能为租赁企业提供节约设备预防性维护的成本。
关键词:预防性维修;人员配置;超承诺期任务量;维修成本
中图分类号:F717 文献标志码:A 文章编号:1673-291X(2022)02-0058-05
引言
随着现代生产设备朝着精细化、高端化、智能化发展,对设备的维修维护的专业化技能提出了更高的要求,需要在生产设备发生故障前就进行及时的预防性维护维修。而高昂的购置费促使越来越多的承租方选择“以租代买”的方式租赁设备。但中小企业无法一次性负担起高额的购置费用,只能使用融资租赁的方式使用设备,长期租赁市场得以高速发展。同时,伴随着经济产业结构的不断优化升级和调整,技术性人才的短缺成为经济发展的首要问题。预防性维修人员作为技术性人员,维修人员的合理配置对于优化设备维修管理具有一定的作用。
传统的通过增加预防性维修人员数量来完成维修任务的做法,可能会造成预防性维修某些时段人员的冗余,造成人力资源的浪费,以及维修企业成本的增加。如果维修人员过少则会大批量的完不成既定的预防性维修任务,从而给企业带来大量损失。所以,合理的人员配置对于预防性维修工作来说尤为重要。
苏析超、伍恒[1]等人提出了基于边际-人工蜂群算法的两层优化人员配置决策架构,通过边际优化算法对人员配置的方案进行迭代优化。郭小威、马登武[2]等人以基于蒙特卡洛方法的PERT网络仿真为核心,选择在遗传算法进化寻优框架下构建优化模型,得到了最优的保障人员配置方案。高丽、徐克林[3]等人将作业分解为子作业层和父作业层,采用遗传算法和动态规划法获取最佳的人工分配方案,减少了柔性生产企业的劳务费用。曹乐、王彪[4]建立了以人员岗位适应度最大和装配线各工位之间作业人员岗位适应度差异最小为目标的装配线人员优化配置模型。谷玉波、贾云献[5]根据维修人员配置的需求,建立了面向任务的维修人员预测模型,减少维修资源的消耗,提高维修效率。Qiang[6]等将整个维护过程描述为3层多代理系统(MAS),并提出了一种基于多主体的机队维修人员配置方法。Abdelrahman[7]根据斯坦伯格博弈模型基于航班延误的运营飞机维修航线问题和维修人员配备问题的相互依存关系,提出了一种协调配置的人员配置模型。Qin [8]研究了飞机重型维修服务公司的维修计划和人员配置问题。Jeroen[9]研究了建立飞机维修公司的员工时间表的问题,通过枚举法进行人员配备和调度决策。
国内外大量的学者对人员的配置进行了一定的研究,但大多文献都是以企业装配、飞机维修等为研究背景,缺乏对预防性维修针对性的研究。本文在预防性维护要求的基础上,考虑预防性维修的人员配置和维修成本优化策略;同时提出了预防性维修的超承诺期任务量的概念,以维修总成本最小为目标,通过MATLAB数值仿真求得最优预防维护人员配置。
一、基本模型
(一)问题描述和假设
本文研究的是考虑多设备预防性维修的超承诺期任务对维修人员的数量进行确定优化。出租方向多个承租方出租不同型号的设备,设备在租赁期内进行等周期的预防性维修。为降低承租方的停工成本,出租方与承租方约定承诺期,租赁设备的预防性维修应在承诺期内完成。由于人员配置太少、任务量太多导致承诺期内无法完成的预防性维修任务称作超承诺期任务,承租方对超承诺期任务造成的停工损失进行惩罚。本文优化的目标是在租期内,出租方保证承租方满意度的基础上均衡维修人员数量,使得设备出租方维修成本达到最小。针对本文所要解决的问题,作出以下假设:
(1)M台租赁设备处于租赁状态,设备从全新状态开始运行,运行过程中无停歇。
(2)承租方分布在同一区域不同地点,每个承租方只租一台设备。
(3)R个维修人员提供维修服务,维修人员每隔固定周期对设备进行等时间的预防性维修,并且修复如新。
(4)当设备在等待及进行预防性维修时,承租方须要停机停产。维修后设备的开机时间忽略。
(5)承租方在设备发生故障后的报修时间相同,采取先报修先服务的原则。
(6)由于维修组能力相当,维修人员全都可以处理预防性维修,因此不考虑每组维修人员之间因维修技术差异引起的时间差距。
符号表示:
R:维修人员的数量
M:出租方维修组的数量
i,s设备编号,i=1,2……N
Ti:设备i的预防性维修周期
tp:出租方向承租方承诺的预防性维修时间
μ:维修人员的技能系数
g:租赁期内每个维修人员的工资水平
(二)维修次数建模
在无限的时间区间内,R个设备的预防性维修呈现出周期性变化,即每隔一段固定时长,预防性维修规律地出现。最小周期由R个设备的各自的预防性维修周期共同决定,为R个设备的各自的预防性维修周期的最小公倍数,可表示为:T=[T1,T2,T3,…,Tn,…,TR]。把无限时间简化缩短在时间T内讨论。
对不同类型的设备i采取周期为Ti的预防性维修,则租赁区间设备i的总预防性维护次数为ni:
ni=(1)
其中,δi为免修阈值,即设备i的运行时间没有达到规定的数值时,则不进行设备的维修活动。
(三)维修人员配置建模
1.预防性维修任务建模
设备i在T周期内所有预防性维修开始时间为Ti,2Ti,3Ti,…,Ti,其中ni=,表示T在周期内设备i最多可进行ni次预防性维修。设备i的预防性维修的任务量为ai,若第t天正好是设备i预防性维修开始的时间,则维修任务增加ai。反之,则不增加。Ai(t)表示在第t天设备i维修任务的增加量,可表示为:
Ai(T)=ai,t=kTi0,t≠kTi (2)
其中k=1,2,3,…,ni
所有维修人员在第t天任务开始时刻的总预防性维修任务量为:
F(t)=S(t-1)+Ai(t) (3)
其中,t≥1,S(t-1)表示為前一天的剩余未完成任务量对第t的影响。若S(t)=0,则表示t天维修任务全部完成,对第t天无影响。若S(t)>0表示还有剩余任务量不能完成。S(0)=0,设备在未开始运行之前不存在剩余未完成预防性维修任务量。
2.预防性维修人员任务安排建模
出租方为保障承租方的满意度,对于所有设备的预防性维修都有一个承诺时间tp,所有设备的预防性维修任务都应该承诺时间tp内完成。
(1)F(t)-μ·R·tp≤0时
表示维修人员可以完成第t天任务开始时刻的所有预防性维修任务量。即在第t天出现的预防性维修任务在承诺时间tp内可以完成。则剩余任务量函数S(t)为:
S(t)=max(F(t)-μ·R),0 (4)
(2)F(t)-μ·R·tp>0时
表示即使所有维修人员都进行作业也不能完成第t天任务开始时刻的所有预防性维修任务量。即在第t天出现的预防性维修任务在承诺时间tp内难以完成。则剩余任务量函数S(t)为:
S(t)=(tp-1)·μ·R (5)
例如,当第t、t+1、t+2天新增任务量分别为A1(t)、0和A2(t+2)时,承诺期为tp,维修人员的技能系数是μ。此时,假设配置维修人员R,若F(t)=S(t-1)+A1(t)>tp·μ·R,保证期内无法完成,出现超承诺期剩余任务量N(t)=F(t)-tp·μ·R,S(t)=F(t)-μ·R;若F(t+1)=S(t)+0<tp·μ·R,若未超过保证期可以完成量,则N(t+1)=0,S(t+1)=F(t+1)-μ·R;若F(t+2)=S(t+1)+A2(t+2)=tp·μ。则承诺期内不存在剩余任务量,N(t+2)=0。S(t+2)=F(t+2)-μ·R。
用N(t)表示第t天超承诺期剩余任务量强度。
N(t)=max(F(t)- μ·R·t),0(6)
对于所有设备的预防性维修需要在承诺时间tp内完成,在超承诺期剩余的维修量为
W=N(t)=max(F(t)- μ·R·tp),0(7)
3.目标函数建模
本文优化的目标是在租期内,出租方保证承租方满意度的基础上均衡维修人员数量,使得设备出租方维修成本达到最小。维修成本包括零部件成本、人工成本和惩罚成本,人工成本为在租赁内R个维修人员的工资总和:
cr=g·R(8)
惩罚成本是指在出租方没有承诺期tp内完成维修任务的惩罚:
cf=λW=λmax(F(t)-μ·R·tp),0(9)
其中,λ是惩罚系数,λ单位为元/超承诺期剩余任务量。
则出租方的总维修成本是C=cr+cf+cl,其中cl是零部件成本。
(四)维修人员模型求解
维修总成本的大小,随着维修服务人员R和惩罚成本的变化而变化,维修服务人员数量的变化,决定着维修的惩罚成本。用递推法对维修人员的数量R的取值范围进行求解。
若第一天的维修任务量可以在保质期内完成,则有:F(1)i(1)/μ·tp≤R。
若第二天的维修任务量可以在承诺期内完成,则有:
F(2)(2)。
S(1)=max(F(1)-μ·R),0=>
F(1)-μ·R≤μ·i(2)
那么维修人员
R≥m+Ai(2)/μ·tp+μ。
若第三天的维修任务量可以在承诺期内完成,则有F(3)+S(2)≤μ·R·tp。
=>F(1)-μ·R≤μ·R·tp+μ·RAi(2)+Ai(3)0≤μ·R·tp+μ·+Ai(3)0≤μ·R·tp-(3)
那么维修人员R的取值如下
R≥m/μ·tp+2μ
同理对于,可得F(t)≤μ·R·tp,可得
R=maxAi(t)/μ·tp+(t-1)μ]
在维修服务期T内,可得维修人员R的集合为B。若R的取值为集合B中最大值表示,在承诺期内所有维修量都能完成,不存在剩余未完成的任务量,即不存在惩罚成本;若R的取值为集合B中的众数mo,表示维修人员能完成维修任务中大多数的任务量,部分任务无法完成,存在惩罚成本。所以,当维修成本最小时,R的取值应介于集合B的最大值与众数之间。
B=[ma/μ·tp+(T-1)μ]
二、计算实例
设备出租方向承租方提供多台设备的无限期的预防性维修服务。多台设备预防性维修呈现出周期性变化,把无限期缩短至多台设备的最小公倍数周期T内讨论。预防性维修承诺期tp=4h,免修阈值δ=T维修人员的技能系数μ=1。多台设备参数取值如表1所示。
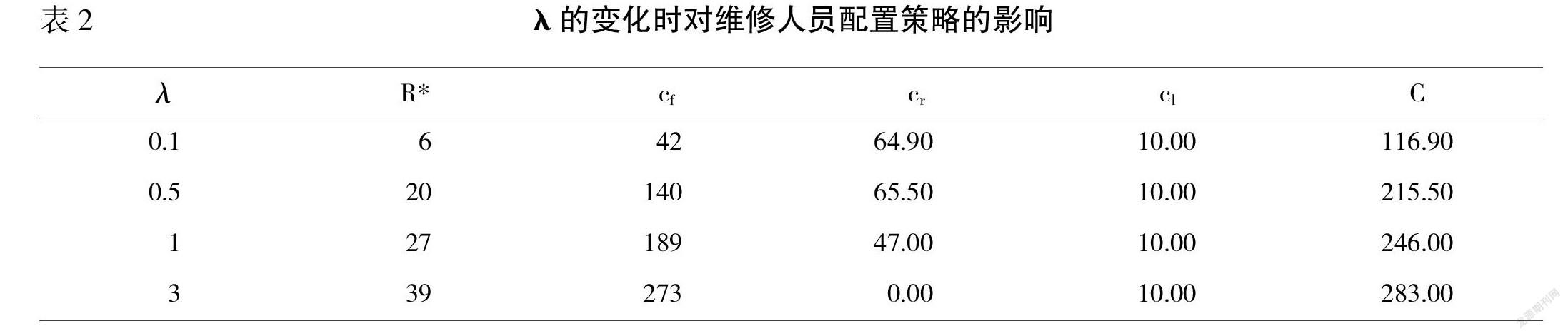
针对以上参数,进行设备的预防性维修惩罚成本的人员配置,并探究惩罚系数对维修人员配置和维修成本的影响,见表2。
由表2可知,预防性维护策略的惩罚系数改变也会引起预防性维护人员配置和出租方维修总成本的变化。当惩罚系数λ变大时,出租方的最优预防性维护人员配置R*增加,维修人员成本Cf变大,超承诺期剩余量惩罚成本Cr变小,出租方的最优平均维修总成本C变大。
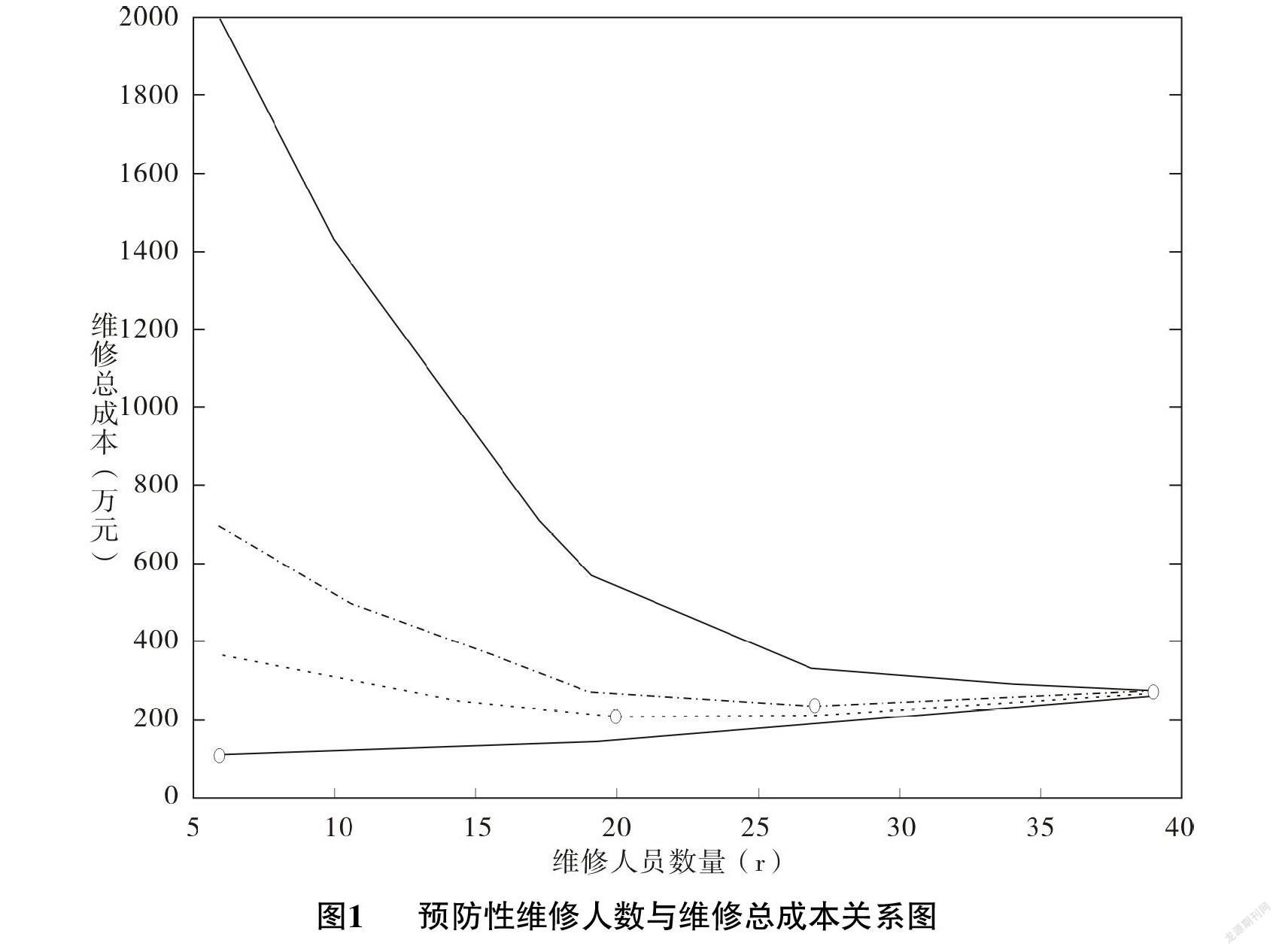
由此可知,出租方出于减少总预防性维修成本的目的,应该平衡维修人员的配置成本和超承诺期剩余任务量之间的关系。一味增加维修人员的数量,并不能减少预防性维修的总成本。
三、结论
本文提出了考虑超承诺任务期惩罚成本下多设备预防性维修的人员配置优化模型。通过算例可知,一般情况下并不是预防性总成本越小,维修人员数量配置就越多、超承诺期剩余任务量就越小。事实上,超承诺期剩余任务量惩罚系数越大,维修人员的配置数量越多。预防性维修总成本受到超承诺期剩余任务量惩罚系数和维修人员薪资的影响。
本文没有研究超承诺期剩余任务量惩罚系数和维修人员薪资的变动对超承诺期剩余任务量和总预防性维修成本造成的影响,这一问题值得今后探究。承租方和出租方可以通過协商制定合理的维修惩罚系数来对人员配置进行更加合理的优化。
参考文献:
[1] 苏析超,伍恒,崔荣伟,张勇.基于边际——人工蜂群算法的舰载机出动保障人员配置——调度联合优化方法[J/OL].北京航空航天大学学报:1-15[2020-03-05].1001-5965.2019.0581.
[2] 郭小威,马登武,邓力.基于PERT网络的航空弹药保障人员优化配置[J].北京航空航天大学学报,2014,40(1):69-74.
[3] 高丽,徐克林,朱伟,童科娜.柔性生产中人员配置模型及其调度算法[J].哈尔滨工业大学学报,2012,44(5):144-148.
[4] 曹乐,王彪,刘飞,李聪波.装配线多技能作业人员优化配置模型[J].重庆大学学报,2010,33(12):21-26.
[5] 谷玉波,贾云献.基于维修任务的维修人员预测模型[J].火力与指挥控制,2013,38(11):107-110.
[6] Qiang Feng,Songjie Li,Bo Sun.A multi-agent based intelligent configuration method for aircraft fleet maintenance personnel[J].Chinese Journal of Aeronautics,2014,27(2).
[7] Abdelrahman E.E. Eltoukhy,Z.X. Wang,Felix T.S. Chan,S.H. Chung. Joint optimization using a leader follower Stackelberg game for coordinated configuration of stochastic operational aircraft maintenance routing and maintenance staffing[J].Computers & Industrial Engineering,2018,125.
[8] Yichen Qin.A branch-and-cut algorithm framework for the integrated aircraft hangar maintenance scheduling and staffing problem[C]//Proceedings of The 2nd International Conference on Information Science and System(ICISS 2019).日本东海大学,新加坡国际计算机科学与信息技术协会,成都亚昂教育咨询有限公司,2019:206-209.
[9] Jeroen Beli?n,Erik Demeulemeester,Philippe De Bruecker,Jorne Van den Bergh,Brecht Cardoen. Integrated staffing and scheduling for an aircraft line maintenance problem[J].Computers and Operations Research,2013,40(4).
Study on Staffing of Preventive Maintenance Worker Considering Over-commitment Task
LIU Wen-qian, JIN Yu-lan
(School of Management, Shanghai University of Engineering Science, Shanghai 201620, China)
Abstract: In order to save maintenance costs and equipment maintenance time, a staff configuration and maintenance cost optimization model for preventive maintenance of multiple equipment was established. The total preventive maintenance cost is taken as the optimization goal, and at the same time, the coordination of the maintenance task and the number of maintenance personnel for the over-commitment period of the lessor and the maintenance penalty for the over-commitment period are comprehensively considered. Using MATLAB simulation to solve the model's optimal staffing and total preventive maintenance costs, examples show that considering the equipment commitment and preventive maintenance over-commitment period task volume penalty cost makes the equipment preventive maintenance more realistic. The situation can provide leasing companies with savings in equipment preventive maintenance costs.
Key words: preventive maintenance; staffing; over-commitment task; maintenance costs
[责任编辑 张宇霞]
3654501908217

