高阶相关峭度反卷积逆滤波器及磁导航野点识别∗
黄卓群 杨光永 程 满 刘 叶
(云南民族大学电气信息工程学院 昆明 650500)
1 引言
AGV是轮式移动机器人的一种典型代表,它通常采用磁条导航来预设行驶路线,将磁条粘贴在地面上,AGV 循迹磁条来进行移动。在AGV 行驶过程中,由于实际环境较为复杂,例如磁条两侧会有磁条碎片或杂散磁场而导致的磁条磁场发生变化使得传感器获取到包含异常点的信号,从而降低了机器人的行驶平稳性,严重时甚至会引起AGV脱轨。异常点指小部分样本严重偏离动态目标变化趋势的伪数据,或远离动态目标随机过程的离群值[1],它是一项主要涵盖传感器技术、信号处理技术、模式识别技术、统计学和算法分析等多种技术与学科为一体的综合性的研究方向,在目标跟踪、图像信号处理、精密测量、病理分析、故障识别、刑事侦查、野生动物保护,甚至宏观经济调控、特困扶贫、反恐防恐、交通指挥、德育教育等领域都有广泛而深远的研究价值和应用前景。异常点作为一种非平稳分布的随机过程,其模式识别和消除是导航信号感知和信号处理的重要任务。1983 年,Dw⁃yer 第一次提出了谱峭度的含义,峭度是一个无量纲参数或者统计量。峭度对信号中的瞬态成分十分敏感,常被用于滚动轴承的状态监测以及故障诊断中。由于磁导航信号在野点干扰下,趋于非平稳分布,故将峭度的含义引入磁导航信号处理办法中。2012 年,McDonald 提出了最大相关峭度反卷积算法,在早期,该算法被用于故障信号的检测。文献[2]以输出信号峭度的绝对值和接近性量度函数的乘积作为目标优化函数,有效避免了人为选择阈值参数和步长。文献[3]以峭度绝对值为对比函数推导出一种一单元ICA-R固定点算法,避免了对比函数二阶导数的计算,简化了运算复杂度。文献[5]提出了一种改进的优化学习算法,在牛顿迭代方向上增加精确线性搜索,从而使得算法的收敛性不依赖于μ的人为选择。文献[7]提出一种改进的基于峭度的盲分离算法,可以自适应地确定激活函数。文献[8]针对双梯度的盲源分离算法进行了研究,以信号的峭度为代价函数对其进行了改进。文献[9]通过建立步长因子与峭度的平方和之间的非线性关系,提出了一种自适应的自然梯度算法。文献[10]提出了一种自适应学习率盲信源分离的自然梯度算法。文献[11]提出了基于峰度的自适应盲信号分离切换算法,用于语音信号盲分离处理。基于峰度的BSS 切换算法在分离前后的信号波形和频谱以及主要评估参数方面具有良好的信号分离效率,具有比JADE FOBI 算法更好的分离效率。文献[12]作者使用最大三阶相关峭度反卷积算法对激光位移信号和多重反射信号进行提取。文献[13~14]提出了常见混合模型的盲源分离方法。文献[15~16]主要阐述了改进的独立分量分析算法。传统的自适应滤波器、高阶统计量滤波器或聚类等方法因缺乏先验知识,难以建立准确的参考模型,出现病态、收敛速度快速降低等问题。因此,本文针对非平稳信号的统计特性,利用相关峭度来度量混合信号变化的统计特性,使用四阶相关峭度反卷积(M4CKD)算法,针对于没有任何参考模型的信号,对其进行盲提取。
2 磁导航信息检测
本实验采用的是八位磁导航传感器,AGV 运行时,采用了磁导航循迹偏差算法,我们将偏差零点设置在导航传感器的中部位置,当地面磁条位于传感器中部时,此时的偏差为0。我们将8 位传感器的中心位置的权值记为8.5,即在该位置AGV是无偏移行驶,AGV 行驶路径图如图1所示。循迹偏差算法的表达式为
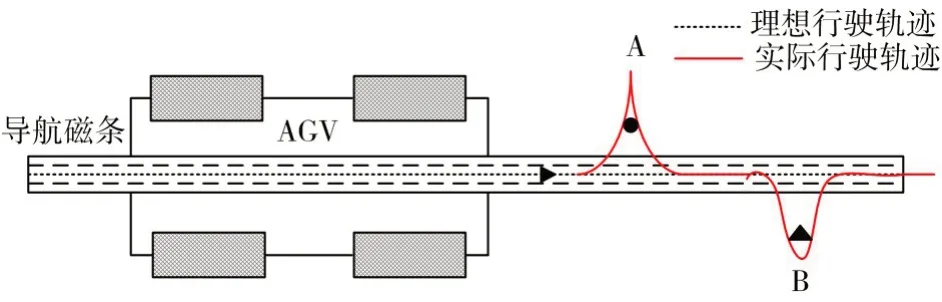
图1 AGV行驶路径图
该式中,Si为每个位置磁导航传感器的权值,M是触发磁导航传感器的个数,ε为偏移距离。
3 算法模型
3.1 最大相关峭度反卷积算法
在2012 年,McDonald 提出了最大相关峭度反卷积算法,该算法早前用于轴承故障检测,对故障信号进行检测。
离散信号为:y(n)=h(n)*x(n)+e(n),x(n)是原始序列,e(n)是噪声,y(n)是输出信号,h(n)是系统函数。该算法主要是要寻找一个FIR 滤波器,使得x(n) 的相关峭度达到最大时,由y(n) 恢复出x(n)。它主要针对的是原始序列中脉冲跳动比较大的信号,对其进行处理,将相关峭度作为代价函数,当原始信号的相关峭度达到最大时,迭代终止。最大相关峭度反卷积算法中相关峭度的定义为
其中,T为信号的周期,M为位移数。M的数量越多,反卷积的脉冲序列也就越多,更有利于提高算法的检测能力。
3.2 算法设计
峭度CK是反映随机变量分布特性的数值统计量是归一化的4 阶累积量。 用公式表示峭度,其中xi为信号值,xˉ为信号均值,N为采样长度,σt为标准差。
磁导航传感器位于AGV 底部的正中心位置,接受到的n维原始信号为U(k)=[u1(k),u2(k),…,un(k)]T,n维观测噪声为N(k)=[n1(k),n2(k),…,nn(k)]T,该混合模型经过一个系统传递函,其中p为延迟时间,则非平稳信号的观测序列X(k)为
设置Wp(k)为逆滤波器,该逆滤波器的传递函数为,可以得到观测序列X(k)和逆滤波器Wp(k)的卷积输出为
其中,y(k)=[y1(k),y2(k),…,yn(k)]T。
设输出矢量y(k)的采样周期为T,定义y(k)的四阶相关峭度C(T)为
其中i=1,2,…,n。当四阶相关峭度达到最大时,逆滤波器获得最优迭代解Wopt(k) ,此时最优解Wopt(k)与H(z)*N(k)的卷积为0,经过滤波器输出的异常点分量为0,磁导航原始信息被提取,表示为
对上式公式进行简化运算,得到M4CKD 算法盲提取信号的输出公式的一般形式为

图2 混合信号提取系统结构框图
3.3 逆滤波器的解
对于求解逆滤波器Wp(k),得到逆滤波器的最优解的必要条件就是使四阶相关峭度对逆滤波器的偏导数为0,即:,带入表达式可得:
因为X(k) 非平稳信号,所以有设:
可得到:
即:
由此可求得逆滤波器的最优迭代解为
其 中 :
4 算法分析
4.1 收敛性分析
四阶相关峭度的变化趋势可以利用反卷积输出的增量来进行考查,进而可求解出四阶相关峭度反卷积算法的收敛条件,分析该算法的收敛情况。设yi+1(k)=(1+τ)yi(k) ,其 中τ是 增 量 因 子,且0<τ<1。将Ci+1(T)在yi(k)处按照泰勒级数展开得:
对上式中的微分项求解可得到:
结合上式,可以得到:
因为0<ρ<1,y1(k)>0,可以得到ρ>0,又因为A-B的迹决定了相关峭度的单调性,因此在反卷积逆滤波器的第i次迭代的过程中,如果有|A-B|≠0 ,则对于A-B的特征值λi满足λi>0,i=1,2,…,n。 根 据 tr(A-B)>0 可 以 推 得ΔCi(T)>0,所以四阶相关峭度函数为单调递增函数。
设终止条件为φ,φ>0,在经过有限次的迭代之后,ΔCi(T) 达到迭代终止条件,即0<ΔCi(T)<φ。此时,四阶相关峭度Ci+1(T)有最大值,所对应得逆滤波器迭代解Wp(k) 为最优解,此时算法收敛,收敛条件可以表示为
4.2 稳定性分析
分析M4CKD 的收敛性和收敛速度可知,当A-B为奇异矩阵,即其特征值λi>0,i=1,2,…,n时,最大四阶相关峭度反卷积算法收敛。考虑A-B的迹,可以得:
即满足上述条件时,四阶相关峭度反卷积算法稳定,且此时AGV 行驶过程中的混合信号被盲提取。
5 算法验证
此实验使用的AGV包含8位磁导航传感器,实验平台如图1 所示。AGV 小车沿着已铺设的轨道运行,在运行过程中,当磁导航传感器感应到地面磁条的信号和野点信号时,通过模拟前端会输出磁条的位置偏移量信息,进而对电机进行差速控制驱动,从而保证AGV能沿着预设轨道进行无偏行驶。

图3 磁导航野点识别实验平台
输入一帧混合观测信号,仿真后将得到输出信号,逆滤波器的单位冲击响应和算法的迭代结果。设置算法迭代次数为20 次,滤波器的单位抽样数为30,采样周期T为5。仿真结果如下所示。
图4是含有噪声的输入信号,根据该图可以看出,在信号幅值处出现3 个波峰,其中波峰最高点对信号的影响最大,此处是引起AGV 行驶轨迹严重偏移阈值的主要原因。

图4 加性噪声输入信号
根据图5 可以看出波峰中带有的噪声信号和其余部位带有的噪声信号经过逆滤波器之后被滤除,恢复出的源信号相较于之前的带有噪声的信号,信噪比更好,变得更加平滑。
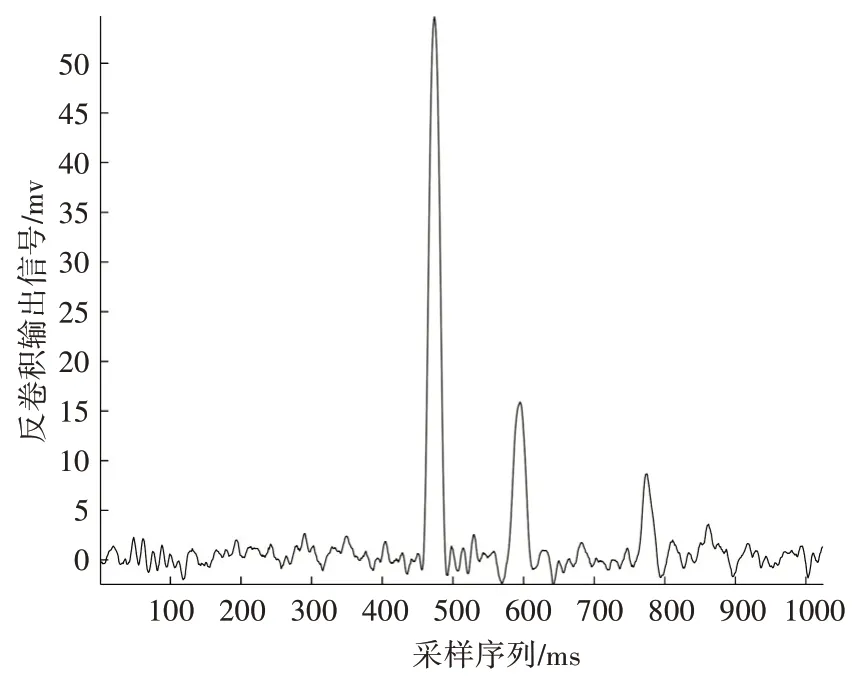
图5 信号经逆滤波器后的输出
图6表示的是混合信号经过采样周期为5的逆滤波器单位响应,该单位响应的图像类似于正弦函数。其幅度范围大概在-0.15~+0.3之间。

图6 逆滤波器的单位响应
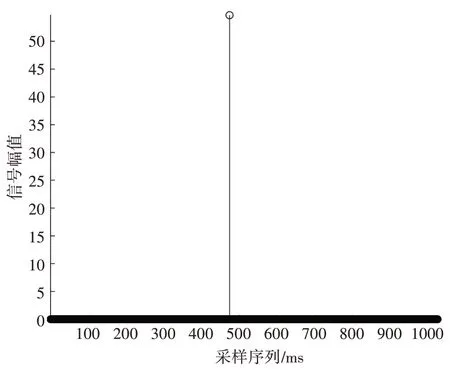
图7 峰值提取
根据信号经过逆滤波器的输出,我们可以提取出最大峰值,通过仿真结果可以得出,信号在x=491处被提取,其幅值为53.7187。
图8是相关峭度与迭代次数的关系,迭代次数在1~6 之间相关峭度在逐渐增大,收敛速度非常快,当迭代次数达到6 次以后,相关峭度达到最大值,此时反卷积算法收敛并且趋于稳定,且盲提取误差达到了9e-4,算法终止迭代。
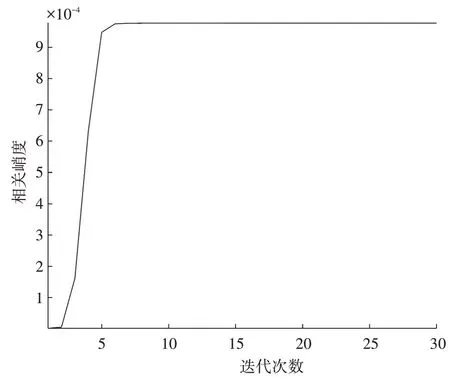
图8 相关峭度与迭代次数
根据图4 和图5 可以看出,在经过逆滤波器之后,输出的信号的幅值都有了提高,主要是因为滤波器的系数所产生的影响,当β越小时,y(k)就越大。因为本文主要是对包含异常点的信号进行盲提取后恢复出源信号,并且滤除其中的噪声。我们在对峰值检测时,检测的是其位移,所以可以忽略幅值变化,其并不会对实验结果产生影响。在进行仿真实验时,如果调整噪声参数,迭代的次数也会发生变化,当调整了高斯白噪声的功率大小,并进行仿真实验时,实验结果如表1所示。

表1 高斯噪声参数与迭代次数的关系
经过多次实验仿真后,可以发现调整噪声参数的大小与迭代次数之间是有一定关系的,随着噪声参数的值越大,迭代的次数会越大,收敛速度将会变慢,而且这些参数控制在0.3~1 之间的效果是较好的,之后的参数值继续增大,混合信号的盲提取效果会变得很不理想,且收敛速度会更加缓慢。所以观测序列的噪声功率大小与算法的收敛速度有关,随着噪声功率越大,峭度的突变信息会越明显,相关峭度的梯度值也就越大。
6 结语
在本文中,以四阶峭度反卷积算法对AGV 行驶过程中所产生的混合信号进行识别和盲提取,通过对滤波器进行迭代,求出最优的迭代解,使AGV能够在预设的轨道上准确平稳的运行。另外对算法的收敛性和稳定性做了论证推导,并对算法进行仿真分析。结果表明,该算法相比于传统的算法,在收敛速度和稳定性方面都有了一定的提升,但在处理复杂度较高的信号时,例如多个波峰的情况下,由于波峰之间的滤波过程也会存在一定的影响,所以输出的结果也会有所不同,该算法的性能有待加强。

