基于MEMS 的推移质卵石运动轨迹研究∗

马 斌 谢世博

（华北水利水电大学信息工程学院 郑州 450046）

1 引言

推移质一般指水流中沿床面滑动、跳跃、滚动以及层移方式运动的泥沙。推移质运动为泥沙运动力学研究的基础，河床变形由它产生，悬移质运动由它引起，因而对泥沙运动和河床稳定等有着重要意义［1~2］。以科学的方法对其进行研究已逾百年，由于该领域涉及内容较为宽广且极为复杂，取得公认的研究成果不多［3~4］。

惯性MEMS 微机电系统传感器，由于其小体积、成本低、低功耗等优点，其应用研究已成为当今科研的热点，MEMS 传感器技术被广泛应用在手势识别、步态检测、空间定位、无人机的姿态导航等方面［5~9］。随着这些技术的广泛应用，传统的推移质石块运动规律研究中，比较常用的技术是数字图像处理技术［10~11］，通过高速摄像机［12~13］和数字图像处理技术来获得推移质石块的基本运动物理参数，进一步获得运动轨迹；还有采用示踪粒子记录三维运动图像［14］。国外有基于四元数的地球引力和磁场测量方向估计算法引入地磁计，利用四元数法对刚体运动轨迹进行研究［15］或开发SPY 方法等对推移质运动进行研究［16］。

和基于高速相机与数字图像处理技术研究推移质石块运动相比，基于MEMS传感器的研究不仅局限于室内研究，本文提出用MEMS传感器内置到石块内部，无论石块在什么场景下运动，内部的传感器总是能提取到石块运动的相关数据，并能读取到PC端。

轨迹推算方面，用MEMS传感器得到的加速度通过物理公式的演算得到每个时刻的速度和位置坐标（这里采用的采样频率为50Hz）；用陀螺仪数据来判断每一个时刻的石块的姿态，为解算石块下一个时刻的位置提供基础。

2 数据采集

传感器采用的是JY901 姿态角度传感器，JY901 姿态角度传感器高度集成了加速度计、陀螺仪等传感器，并且内部集成了姿态解算器，配合卡尔曼滤波，输出的稳定性较好。JY901 姿态角度传感器具体结构如图1所示。

图1 JY901姿态角度传感器

2.1 加速度

加速度的测量是通过加速度计实现的，并且分为X、Y、Z三个方向。在图1 中，右上方标出了模块的轴向，其中右向为X轴，上向为Y轴，垂直向外为Z轴，旋转的方向按照右手法则，即右手的大拇指指向轴向，四指握拳，此时绕着这个轴旋转的方向就是四指弯曲的方向。在设置界面校准加速度之后，加速度计即可使用。图2为传感器设置界面。

图2 传感器设置界面

2.2 角速度

角速度的测量是通过陀螺仪传感器实现的，并且分为X、Y、Z三个方向。因为石块的运动是三维的，下一个时刻和当前时刻的坐标系不可能完全重合，所以每个时刻的姿态都在变化，每个时刻都有相对于上一时刻转过的角度，陀螺仪传感器的测量值为某时刻相对于坐标系的转动角速度。在设置界面校准陀螺仪之后，陀螺仪即可使用。

3 数据处理

实验过程中材质是3D 打印的，传感器是直接固定在载体上，因此得到的是以载体为参照物的坐标系（假设此坐标系为a 系），而真正在姿态求解过程中需要得到载体的地理坐标系（假设此坐标系为b 系），常见的姿态更新算法有欧拉角法、方向余弦法、四元数法，本文中采取四元数算法来进行姿态解算。所谓的姿态解算，就是求出当前的机体坐标系a 相对于地理坐标系b 的变化。由于a 系和b 系均为直角坐标系，各轴之间始终保持直角，所以可将坐标系理解成刚体，当只研究两个坐标系间的角位置关系时，可理解成刚体的定点转动。而刚体定点转动这个变化可以通过一个变换矩阵来表示，这个矩阵包含了刚体的所有姿态信息。

3.1 坐标转换

欧拉角能够表示运动的旋转物体投影到空间坐标轴上，在惯性系统中，欧拉角描述物体的旋转的旋转顺序：首先为偏航角（Yaw），然后为俯仰角（Pitch），最后是滚转角（Roll），反映到坐标轴上为先绕Z轴旋转，再绕Y轴旋转，最后绕X轴旋转。欧拉角表示的坐标变换矩阵见式（1）。

3.2 四元数

在平面（x，y）中的旋转可以用复数来表示，同样的三维中的旋转可以用单位四元数来描述。定义四元数为

对于i、j、k本身的几何意义可以理解为一种旋转，其中i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转，j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转，k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转，-i、-j、-k分别代表i、j、k旋转的反向旋转（如图3 所示）。

图3 四元数概念图

表1为四元数的几种表达方式。

表1 四元数的表达方式

3.3 算法步骤

算法总体设计图如图4。

图4 算法总体设计图

1）重力加速度规范化处理

加速度计数据规范化处理，就是把加速度计的三维向量转换为单位向量，因为是单位矢量到参考物的投影，所以要把加速度计数据单位化，其实规范化改变的只是这三个向量的长度，方向并没有改变，也是为了与单位四元数对应。

2）算法更新

（1）将当前姿态的重力在三个轴上的分量分离出来，把四元数换算成方向余弦中的第三行的三个元素，就是地理坐标系的Z轴的重力向量。

（2）注意是地理坐标系（b 系）到载体坐标系（a系）。

（3）惯性测量器件测量的都是关于a 系的值，将a系转换到b系进行导航参数求解。但是这里并不需要这样做，因为这里是对陀螺仪进行补偿。

（4）此处更新的三个向量就是上一次的欧拉角的坐标参考系换算出来的重力的单位向量。

3）向量差积

传感器中测得的量为物体运动的实际重力分量，算法更新得到的是推算出来的重力分量，它们之间的误差向量，就是陀螺积分后的姿态和加速度计测出来的姿态之间的误差。这个叉积向量仍旧是位于机体坐标系上的，而陀螺积分误差也是在机体坐标系，而且叉积的大小与陀螺积分误差成正比，正好拿来纠正陀螺。由于陀螺是对机体直接积分，所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。

4）四元数的微分方程

四元数的微分方程为

矩阵形式为

式中，wx，wy，wz为陀螺仪的测得量，通过此式更新四元数可以求得q0，q1，q2，q3。

5）四元数的规范化处理

由于计算中存在误差，并且陀螺仪在测值的过程中一直在累积误差，而用来表征旋转的四元数应该是规范的四元数，所以在此需要对四元数规范化处理。用处理过的四元数去求重力分量。

由此，用得到的实际加速度和Δt进行积分，再用姿态矩阵求解位置，就能得到石块在空间中的运动轨迹。

4 实验结果

本次实场景采取室内无水水槽条件和实验室相结合进行，传感器数据采集间隔为0.02s，实验测得的部分原始加速度和角速度如表2所示。

表2 传感器采集的部分数据

其中vx，vy，vz为接收到的石块运动过程中的部分原始加速度，加速度的单位为gm2/s；wx，wy，wz为接收到的石块运动过程中的部分原始加速度，角速度的单位为rad/s。

部分解算轨迹如图5~8所示。

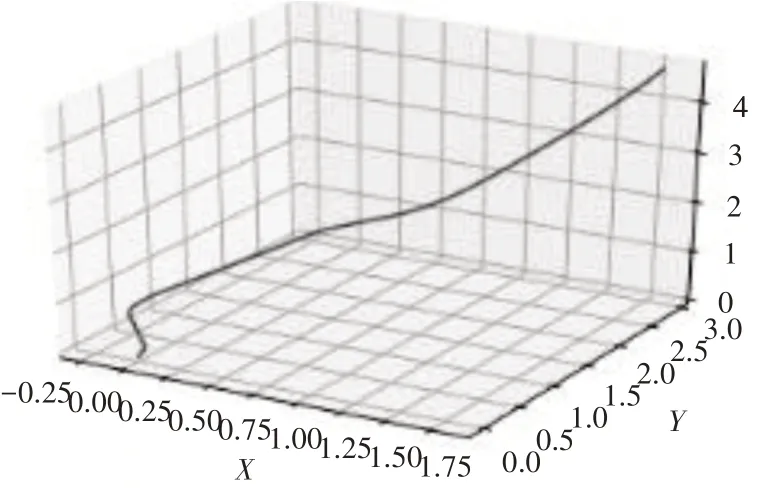
图5 运动轨迹

图6 运动轨迹

图7 运动轨迹

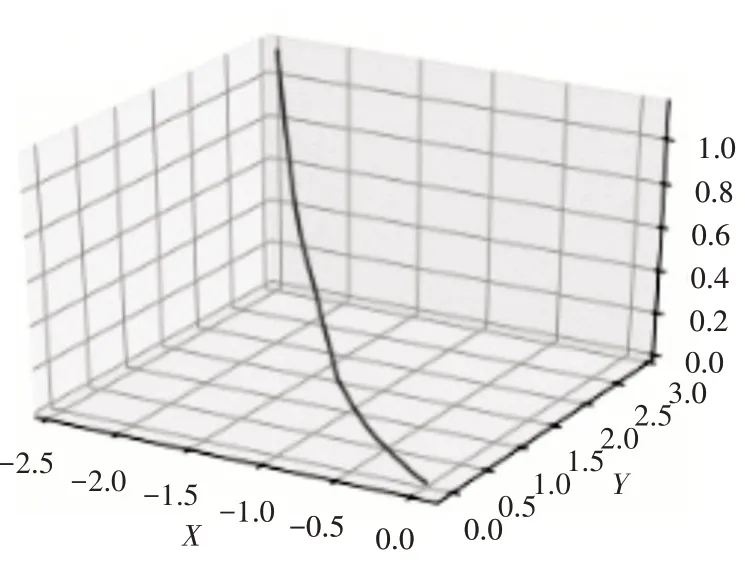
图8 运动轨迹

5 结语

本文提出了一种基于MEMS 传感器的推移质中石块运动轨迹解算方法。通过加速度和角速度计的数据采集，通过不断地四元数更新结合物理学加速度、角速度，使石块的运动落实到空间中的每个点上，通过规范化处理和向量叉积减小误差，使石块运动展现的更立体。后续可以结合机器学习和深度学习，通过大量训练得到一定条件下石块运动的特征，在发生与之关的地质灾害时可以进行有效的预防。