EC细网格对黔南州温度预报的订正研究*

赵 杰，陈 波，莫乙冬，潘启学，顾 欣

(贵州省黔南布依族苗族自治州气象局，贵州 都匀 558000)

0 引言

随着数值预报的发展，其所提供的定量要素预报准确率也有所提升，但是由于大气混沌性及初始场的不确定性，再好的数值预报模式也会产生一定的偏差，尤其在贵州地区，受地形影响大，偏差更为明显，因此数值预报的应用需要进行误差订正。目前国内使用EC模式较多，且已有一些学者对于当地的EC模式误差进行了分析和订正[1-7],贵州部分地区也对当地的温度订正方法进行了研究[8-11],但是针对黔南地区的温度订正的研究还未系统性展开，因此急需开展本地的温度订正研究。

针对模式误差的订正研究采用较多的方法为滑动平均法[1,13]，双权重滑动平均法[1,12],多项式拟合法[8-9]等，这些方法均相对于EC模式预报有提升，但不同月份、不同地区订正效果有所差异，且时效越长订正效果越差。本文还采用最佳系数法对EC模式温度预报进行订正，通过对4种方法的整体订正情况以及各月各站点的订正情况进行对比分析，拟对本地的温度预报给出指导性意见。

1 资料和方法

本文选取EC细网格2 m温度预报场资料，资料起止时间为2019年6月27日—2020年7月3日逐日08时和20时起报场数据；实况资料为相应时间段黔南州12个国家站的观测数据。

利用Python处理数据，将EC格点资料采用双线插值法[14]得到黔南每个国家站点的预报数据，然后再对1～7d的数据处理得到未来7 d的预报逐日最高气温(下称高温)与逐日最低气温(下称低温)。本文采用的订正方法除了滑动平均法、双权重滑动平均法、多项式拟合法外，为了找到更符合黔南州的订正方法，结合黔南州预报员的预报经验，还采用了最佳系数法：对某个站给一个系数k，k从m开始每次加0.1 ℃直到n，该站前p天的EC细网格最高(低)温度预报值均加上k值，统计出该k值条件下该站前p天的准确率和平均绝对误差。取准确率最高的k值为该台站的最佳系数，若准确率相同，则取平均绝对误差更小的k值为该台站的最佳系数。公式表达如下[12]：

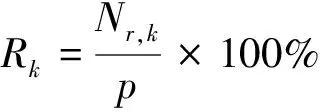
(1)

(2)

公式(1)中Nr,k表示某一台站系数为k时前p天|Tf+k-To|≤2的次数，Tf为EC细网格预报温度，T0为实况温度。K的取值范围为(m,n)，通过前期对EC细网格温度预报误差的研究，黔南州的温度预报误差基本在-5～7 ℃之间，因此本文取k=(-5，7)。

2 滑动周期敏感性

为了确定不同的滑动周期对订正效果的影响，在用不同的滑动周期订正后，将前3 d的高温和低温预报准确率进行比较，得到图1(分为08时起报和20时起报)。对于低温预报(图1a、图1b)，前72 h时效两种起报场的预报准确率基本随滑动周期的增大而提升，但是10 d以后提升不是很明显，其中72 h时效20时起报场(图1a)的预报准确率在滑动周期为10 d时达最大，随着滑动周期的增大预报准确率反而略有下降。对于高温预报(图1c、图1d)，24 h时效两种起报场均在滑动周期为10 d时预报准确率达到最大，后续随着滑动周期的增大，预报准确率反而有所下降；48 h时效20时起报场的预报准确率基本随滑动周期增大而增大，但是10 d以后升幅缓慢，08时起报场的预报准确率随着滑动周期的增大略有下降；72 h时效两种起报场预报准确率随滑动周期增大而升高。总的来看，滑动周期在10 d以内时，预报准确率随着周期的增大而升高，随着滑动周期的增大，预报准确率升幅缓慢或者有所下降。这与吴钲[13]等人的研究一致，因而在后续分析中采用10 d的滑动周期。

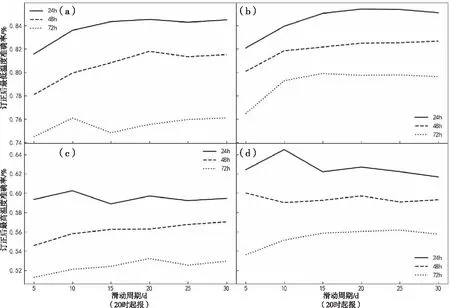
图1 前72 h时效最高温和最低温的预报准确率随滑动周期的变化Fig.1 The prediction accuracy of the highest temperature and lowest temperature in the first 72 h changes with the sliding period

3 订正结果分析

3.1 全年分析

表1为4种方法订正前后各时效温度预报准确率的差值。总的来说订正后高温预报的准确率仍然明显低于低温预报的准确率，但高温预报准确率7 d内均有明显提高，4种方法的7 d平均预报准确率分别提升了12.70%～17.84%，其中最佳系数法提升最明显，其次是多项式拟合法。低温预报准确率有一定的提高，4种方法的7 d平均预报准确率分别提升了1.14%～2.86%，其中最佳系数法提升最明显，其次是滑动平均法。

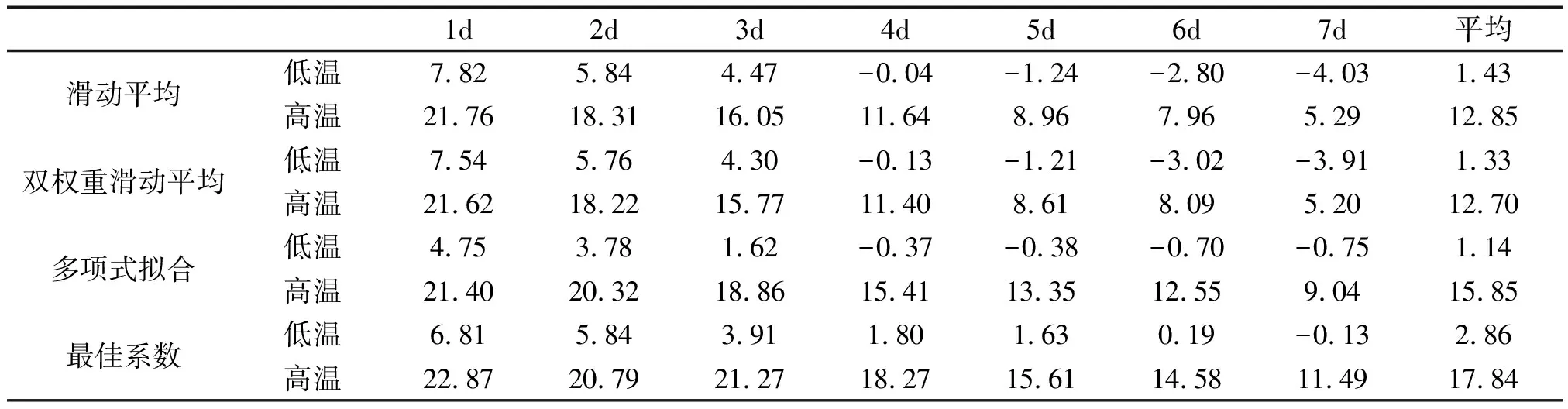
表1 订正后各时效温度预报准确率与订正前的差值Tab.1 The differences between the accuracy of each aging temperature forecast after correction and before correction

对于高温预报，预报时效越短订正后预报准确率提升越明显，4种方法第1 d预报准确率均提升了22%左右，第7 d预报准确率只提升了5.20%～11.49%，预报时效越长几种方法之间的差距越明显，第1 d最佳系数法比双权重滑动平均法预报准确率多提高1.25%，到第7 d则多提高了6.29%。

纵观4种方法发现最佳系数法预报准确率提升最明显，其次是多项式拟合法。

对于低温预报，采用滑动平均法、双权重滑动平均法、多项式拟合法订正时，前3 d预报准确率在订正后有所提升，时效越短提升越明显，第1 d分别提升4.75%～7.82%，其中滑动平均法提升最明显，第4 d开始预报准确率在订正后反而有所下降，第7 d下降幅度为0.75%～4.03%，多项式拟合法下降幅度明显小于滑动平均法和双权重滑动平均法。在采用最佳系数法订正时，低温预报准确率基本都有所提升，预报时效越短提升越明显，到第7 d时预报准确率略有下降，降幅为0.13%。纵观4种方法，低温预报在前3 d采用滑动平均法订正后预报准确率提升最明显，第4 d开始采用最佳系数法订正后预报准确率提升明显。

3.2 逐月分析

为了体现出4种订正方法在各月的表现情况，由于第4 d开始各种方法的表现情况不一样，故以下列举出了24 h时效和120 h时效4种方法订正后的逐月预报准确率和平均绝对误差。图2为滑动平均法(图2a)和双权重滑动平均法(图2b)订正后的预报准确率和平均绝对误差，可以看出两种订正方法效果比较近似，订正后高温预报的平均绝对误差仍然明显低于低温预报，但是二者均有明显的降低。

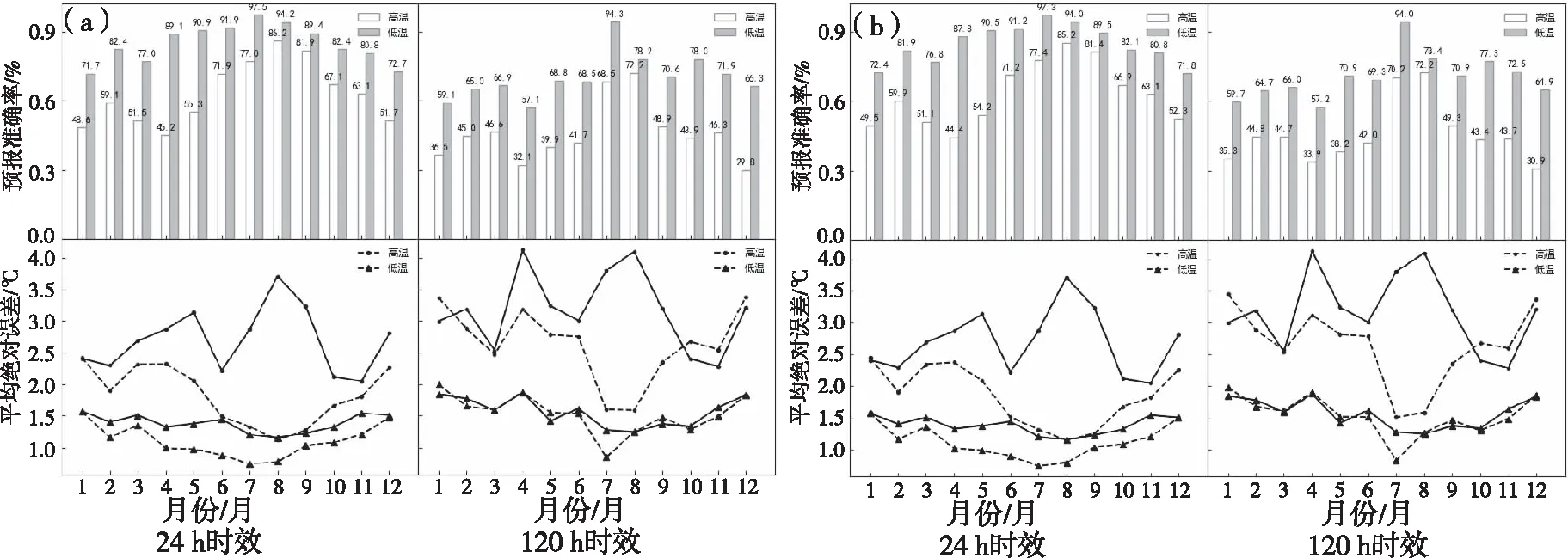
图2 24 h和120 h预报时效订正后逐月准确率及平均绝对误差(a:滑动平均，b:双权重滑动平均法)Fig.2 The monthly accuracy and average absolute error of 24 h and 120 h forecasts after correction(a:Moving average;b:bi-weight moving mean)

从平均绝对误差来看，对于高温预报，24 h时效的平均绝对误差在5月，7—9月订正效果比较明显，误差降幅均超过1 ℃，其中8—9月降幅超过2 ℃，最大降幅为8月的2.6 ℃，120 h时效的平均绝对误差在7—8月订正效果明显，误差降幅超过2 ℃，最大为8月的2.5 ℃。对于低温预报，24 h时效的平均绝对误差在5—8月订正效果较为明显，平均绝对误差降幅超过0.4 ℃，最大降幅为6月的0.6 ℃，120 h时效的平均绝对误差仅在7月降幅较为明显，降幅为0.4 ℃。

从订正后准确率来看，对于低温预报，24 h时效预报准确率在5—8月较高，两种方法均超过了90%，最高为7月，超过了97%，120 h时效预报准确率仅在7月超过了90%，其余月份均低于80%。对于高温预报，24 h时效预报准确率在6—9月较高，两种方法均超过了70%，其中8—9月超过了80%，120 h时效预报准确率在7—8月较高，两种方法均在70%左右。

图3为多项式拟合法(图3a)和最佳系数法(图3b)订正后的预报准确率和平均绝对误差，两种方法订正后高温预报的平均绝对误差仍然大于低温预报，与两种滑动平均法的误差相比，最大的不同在于120 h时效的低温预报，多项式拟合法订正后的平均绝对误差与订正前接近，基本没有出现订正后平均绝对误差反比订正前更大的情况，这也侧面说明在120 h时效后，多项式拟合法订正比两种滑动平均法更稳定，对于最佳系数法，2月、4月和12月的平均绝对误差订正后比订正前更大，且误差大于两种滑动平均法，但是其他月份误差值小于两种滑动平均法。下面从准确率方面分别讨论多项式拟合法和最佳系数法与两种滑动平均法的差异。

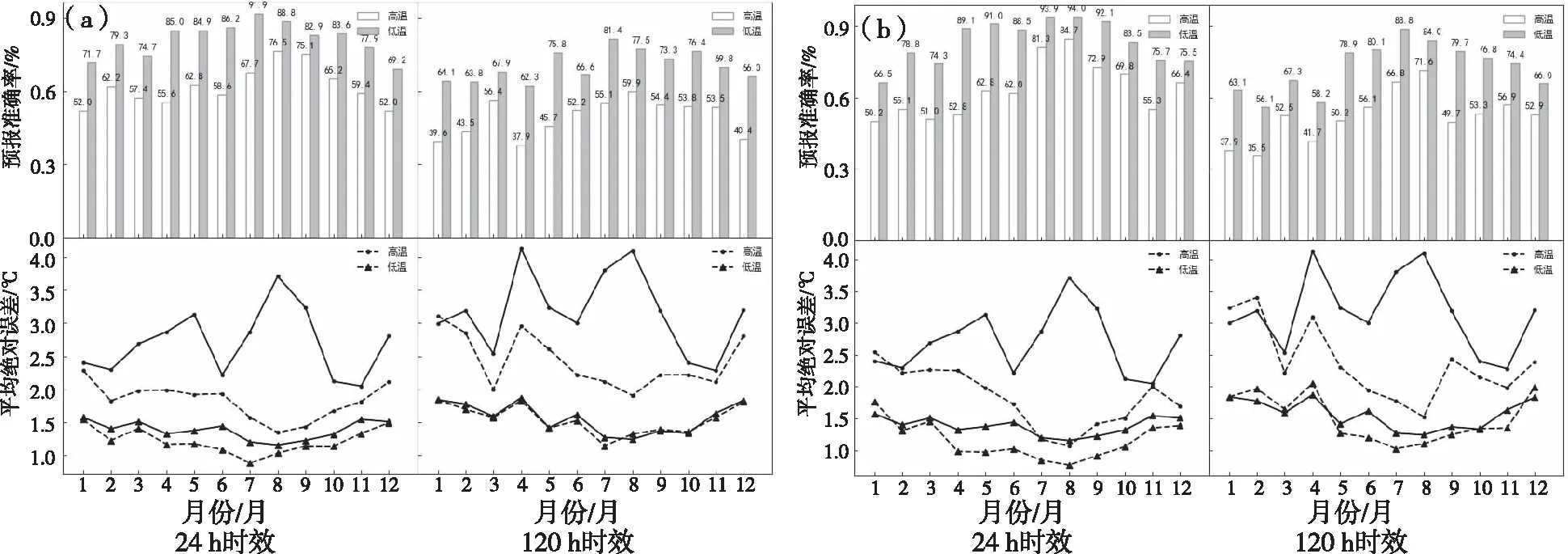
图3 24 h和120 h预报时效订正后逐月准确率及平均绝对误差(a:多项式拟合，b:最佳系数)Fig.3 The monthly accuracy and average absolute error of 24 h and 120 h forecasts after correction(a:Polynomial fitting;b:Best coefficient)

对于多项式拟合法，从高温预报准确率来看，24 h时效在1—5月相对两种滑动平均法有所提升，升幅在3%以上，尤其4月提升达到10.4%，但是6—11月较两种滑动平均法有所降低，降幅在2%以上，最低6月达13.3%；120 h时效在1月、3— 6月、9—12月相对两种滑动平均法有所提升，升幅在3%以上，尤其12月提升10.6%，其次6月提升10.5%，但是7—8月较两种滑动平均法有明显降低，降幅分别为13.4%和12.3%。从低温预报准确率来看，24 h时效除了1月和10月以外，其余时间较两种滑动平均法均有所降低，降幅2.3%～6.5%；120 h时效在1月、3—5月、9月较两种滑动平均法有所提升，升幅在1%以上，其中1月和4月升幅在5%以上，其余时段均有所降低。

对于最佳系数法，从高温预报准确率来看，24 h时效在1月，4—5月、7月、10月、12月相对两种滑动平均法有所提升，升幅在2%以上，最大12月达14.7%，其余月份较两种滑动平均法有所较低，最大降幅6月达9.9%；120 h时效除2月、7—8月相对两种滑动平均法有所降低外，其余时段均有所提升，升幅在0.8%～23.1%，最大也是出现在12月。从低温预报准确率来看，24 h时效4—5月、9—10月和12月相对两种滑动平均法有所提升，升幅在0.1%～2.8%，其余时段较两种滑动法有所降低，降幅在0.2%～5.2%；120 h时效除了2月、7月、10月和12月较两种滑动平均法有所降低外，其余均有明显的提升，尤其5— 6月，升幅达10%以上。

纵观4种方法均在7—9月订正效果较好，这与前期EC预报温度预报的误差分析结论一致。最后将120 h时效前后每个月高温预报和低温预报的最优方法整理出表2。从表中可以看出120 h时效前滑动平均法订正效果较好，120 h时效后最佳系数法订正效果更明显，这与前面的结论相一致。在1月、3— 4月、10月多项式拟合法表现突出，2月、7—8月则是滑动平均法更为突出，5— 6月、9月、11—12月则最佳系数法更突出。

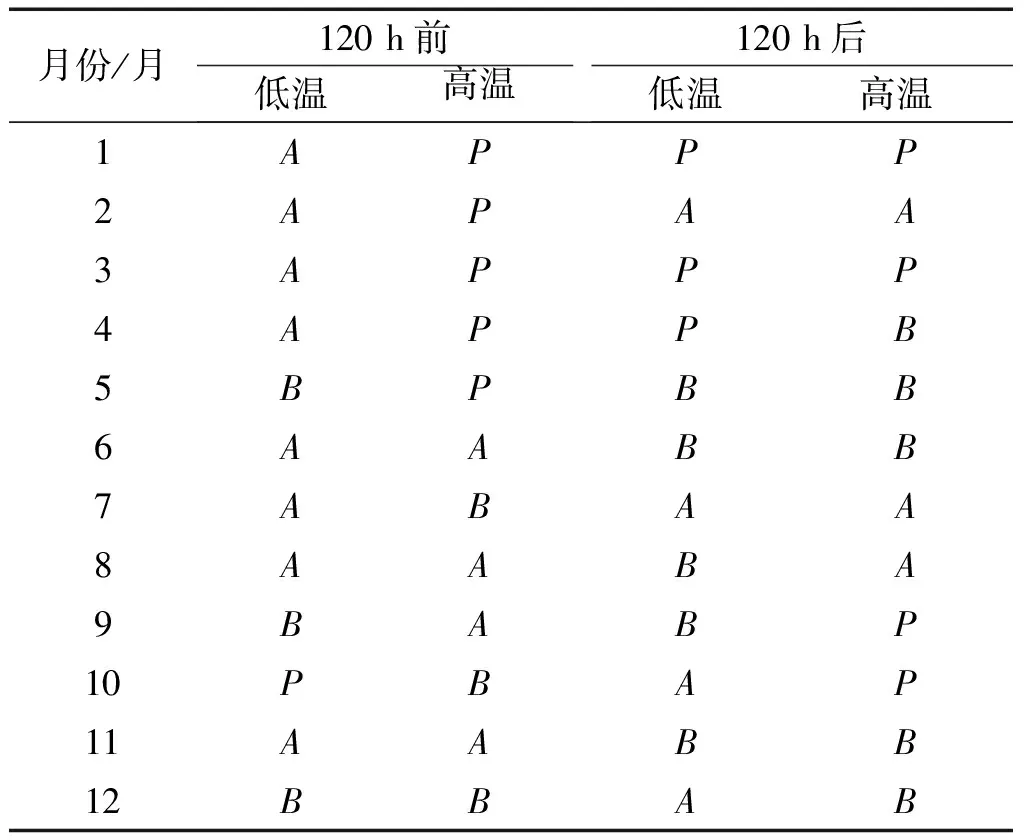
表2 120 h时效前后逐月最佳订正方法

3.3 站点分析

从前面的研究可以看到，EC低温预报的准确率较高，而高温预报的订正效果明显，为了检验各站点的订正效果，做了几种方法订正后高温预报的平均绝对误差分布图，由于滑动平均法与双权重滑动平均法订正效果相似，故略去双权重滑动平均法分布图。从24 h时效的绝对误差分布(图4)来看，总的来说3种方法均有明显的提升，订正前(图4a)全州平均绝对误差在1.8 ℃(瓮安)～3.8 ℃(荔波)之间，几种方法订正后绝对误差均在1.6 ℃以下，其中南部地区的罗甸、荔波、三都订正效果最为明显。滑动平均法(图4b)和最佳系数法(图4d)在黔南州西部、北部及东南部地区订正效果明显，多项式拟合法(图4c)在中西部地区订正效果明显。对于黔南州西部地区，多项式拟合法订正后平均绝对误差在1.2 ℃以下，明显优于另外两种方法。

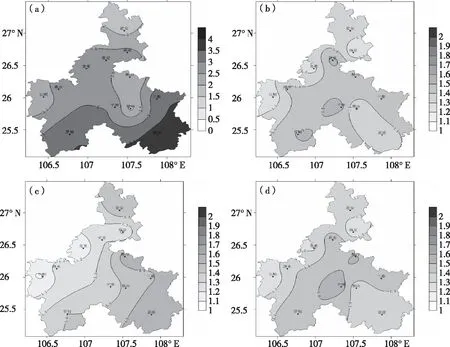
图4 24 h时效订正前后平均绝对误差分布(a:订正前;b:滑动平均法;c:多项式拟合法;d:最佳系数法)Fig.4 Distribution of the average absolute error before and after correction (24 h)(a:Before correction;b:Moving average;c:Polynomial fitting;d:Best coefficient)

图5为120 h时效几种方法订正前后的高温预报平均绝对误差分布图。可以看到几种方法订正后全州平均绝对误差均有明显的降低，但是滑动平均法与其他两种方法相比，订正后的平均绝对误差偏高，订正效果较偏差。订正前(图5a)全州平均绝对误差在2.5 ℃(瓮安)～4.1 ℃(荔波)之间，滑动平均法(图5b)订正后全州误差在1.9 ℃(长顺)～2.4 ℃(都匀)之间，在州西部、南部地区订正效果较好，多项式拟合法(图5c)订正后全州误差在1.6 ℃(长顺)～2.2 ℃(荔波)之间，在州西部地区订正效果较好，最佳系数法(图5d)订正后全州误差范围在1.8 ℃(长顺)～2.1 ℃(贵定)之间，在州西部、东南部地区订正效果较好。

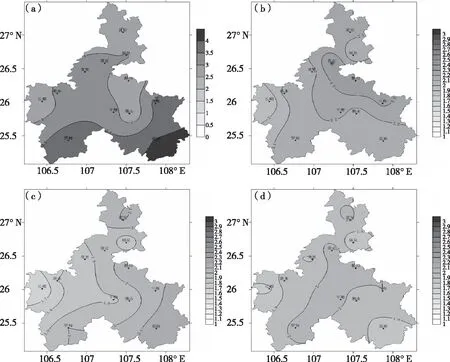
图5 120 h时效订正前后平均绝对误差分布(a:订正前;b:滑动平均法;c:多项式拟合法;d:最佳系数法)Fig.5 Distribution of the average absolute error before and after correction (120 h)(a:Before correction;b:Moving average;c:Polynomial fitting;d:Best coefficient)

总的来看，3种方法在黔南州西部地区均有不错的订正能力，但多项式拟合法订正效果更好，另外多项式拟合法在黔南州中部地区也优于另外两种方法。黔南州东南部地区滑动平均法与最佳系数法均有不错的订正表现，但是在120 h时效后滑动平均法订正效果明显下降。州北部地区最佳系数法订正效果更为明显。

4 结论与讨论

本文通过滑动平均法、双权重滑动平均法、多项式拟合法、最佳系数法4种方法对EC细网格2 m温度预报进行订正，得出以下结论：

① 4种方法订正后预报准确率均为最低气温明显高于最高气温，但是最高气温订正效果明显优于最低气温，最高气温7 d平均准确率分别提升了12.70%～17.84%，最低气温7 d平均准确率分别提升了1.14%～2.86%。对于高温预报，最佳系数法准确率提升最明显，其次是多项式拟合法，预报时效越长几种方法之间的差距越明显。对于最低气温，前3 d采用滑动平均法订正准确率提升最明显，第4 d开始则采用最佳系数法订正准确率提升明显，其余方法反而出现下降。

②从逐月分析来看，4种方法均在7—9月订正效果最明显，120 h时效前滑动平均法订正效果较好，120 h时效后最佳系数法订正效果更明显，其次是多项式拟合法。在1月、3— 4月、10月多项式拟合法表现突出，2月、7—8月则是滑动平均法，5— 6月、9月、11—12月则最佳系数法更突出。

③从地理分布来看，4种方法均在州西部地区订正效果更为明显，其中多项式拟合法最明显。州中部地区多项式拟合法订正效果明显，州东南部地区最佳系数法与滑动平均法订正效果更为明显，但在120 h时效后滑动平均法的订正效果明显下降。州北部地区最佳系数法订正效果更为明显。

本文4种方法订正后的预报准确率仅与订正前的EC预报准确率做对比，还没有与中央台预报、省台指导预报、黔南州预报员的预报质量作对比，该项工作将在后续的研究中继续开展，不在此文做讨论。