基于IPSO-ELM模型的尾矿坝稳定性分析

赵允坤，胡 军，栾长庆，张瀚斗

(1.辽宁科技大学土木工程学院，辽宁 鞍山 114051；2.鞍钢集团矿业弓长岭有限公司选矿分公司，辽宁 辽阳 111008；3.鞍钢集团有限公司东鞍山烧结厂，辽宁 鞍山 114041)

尾矿坝是一种特殊的矿山工业构筑物，用于堆放和处理尾矿等矿山固体废弃物和污染物，类似于水库，在矿山区的安全及环境保护和治理中起到很大作用[1]。尾矿坝作为一种潜在的泥石流危险源，一旦发生溃坝事故，将会造成严重的人员伤亡、财产损失和环境污染等问题，因此尾矿坝的安全运行越来越受到国家和相关企业的重视。尾矿坝的稳定性受多种因素共同影响，其安全系数F与它的影响因素之间存在复杂的关系，传统的智能算法训练效果不理想。近年来，随着人工智能算法的发展，人们也开始将其应用于岩土工程等各个领域，实验结果表明预测效果较好。臧焜岩等[2]针对现有研究方法在预测露天矿边坡稳定性时存在适用性不强和误差大的问题，结合BP神经网络具有容错性和自适应性等优点，基于遗传算法对BP神经网络进行改进，提出一种露天矿边坡稳定性预测模型，取得较好的预测效果，但是BP神经网络需要大量的训练样本，训练时间比较长，容易陷入局部极小值点；黄俊等[3]针对传统边坡稳定性预测模型的不足，首先利用网格搜索法粗略寻优，确定参数范围，然后再利用粒子群算法进行二次寻优，进而提出一种基于网格搜索和粒子群优化的支持向量机模型(GS-PSO-SVM model)，将该模型应用于边坡稳定性预测，取得一定的预测效果。虽然支持向量机(SVM)是目前使用较多的模型之一，其模型简单，鲁棒性强，在解决小样本、非线性问题上表现出诸多优势，但是该模型需要设置大量参数，选取合适基函数等，参数的设置对泛化能力和精确度都有较大的影响。基于智能算法对尾矿坝稳定性进行精准的预测，在一定程度上可以大大减轻滑落事故等灾害对工程建设、人民生命财产安全以及生态环境的影响。

随着计算机技术以及人工智能算法的发展，极限学习机(extreme learning machine，ELM)广泛应用于各个领域，该算法是一种从前馈神经网络基础上发展起来的机器学习方法，和传统智能学习算法相比，其随机选择隐含层节点，以解析计算的方式确定输出层权值，理论上能以较快的速度获得较好的泛化性能，具有泛化能力强、收敛速度快等优点[4-5]；但是也存在一定缺点，随机产生隐含层节点的权值和阈值可能出现无效的隐层节点，导致泛化能力不足。为了更高精度、更加快速地寻优，本文引入自适应权重法来改进基本粒子群算法，有效增加了粒子多样性，避免在寻优过程中陷入局部最优，将改进的粒子群算法(IPSO)对极限学习机初始输入权值和阈值进行优化，进而建立IPSO-ELM模型，并将该模型运用到尾矿坝稳定性预测的实际工程中，结果表明该模型有较好的学习能力，预测精度高，在评价尾矿坝稳定性方面是一种有效的方法。

1 极限学习机(ELM)

极限学习机(extreme learning machine，ELM)是HUANG等[5]提出的一种基于前馈神经网络基础上发展起来的机器学习方法，该模型由输入层、隐含层和输出层三层结构组成，在训练过程中，不需要调整输入层与隐含层之间的初始权值和隐含层阈值，只需对隐含层之间的节点个数进行设置，便可通过最小二乘法计算输出权值完成训练[6-7]。该模型与传统的神经网络相比，具有训练速度快、准确度较高、参数设置较简单、泛化能力较好的优点，目前已广泛应用于坝体稳定性分析领域。网络结构如图1所示。

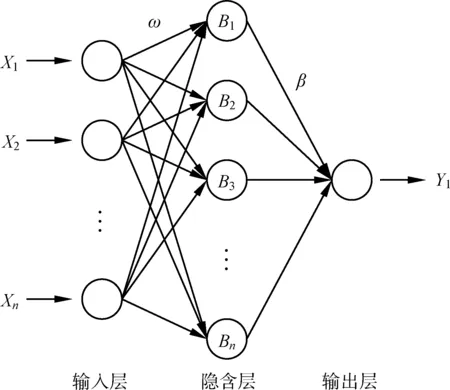
图1 极限学习机网络结构示意图Fig.1 Structure diagram of extreme learning machine network

假设有N个任意的样本(Xi,Yi),其中Xi=[xi1,xi2,xi3,…,xin]T∈Rn，Yi=[yi1,yi2,yi3,…,yin]T∈Rm，则单隐含层前馈型神经网络的输出为式(1)。

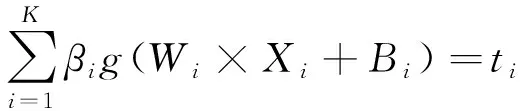
(1)

式中：K为隐含层节点个数；g(x)为隐含层激励函数；Wi=[wi,1,wi,2,wi,3,…，wi,n]T为输入层与隐含层之间的连接权值向量；βi=[βi,1,βi,2,βi,3,…，βi,n]T为输出层与隐含层之间的连接权值向量；Bi为隐含层神经元节点中第i个节点的偏置值；Wi×Xi为Wi与Xi的内积。

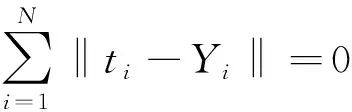
(2)

即存在βi、Wi、Bi使式(3)成立。

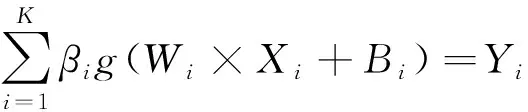
(3)

式(3)可通过矩阵表示为式(4)。

Hβ=T

(4)

式中：H为隐含层的输出矩阵；β为输出权重；T为期望输出。当模型中选定的隐含层激励函数g(x)无限可微时，输入权值ω和隐含层偏置B可以随机初始化，输出权值β可通过最小二乘法求得该函数的最小范数见式(5)。

β=H+×T

(5)

式中，H+为矩阵H的Moore-Penrose的广义逆。

2 改进的粒子群算法优化极限学习机(IPSO-ELM)

2.1 基本粒子群算法(PSO)

基本粒子群算法的产生来源于对简化的社会模型的模拟[8]，由KENNEDY等[9]提出。假设在d维搜索空间中，存在规模为n的粒子种群，各粒子的运动速度和位置分别按照式(6)和式(7)进行更新。

Vid(t+1)=Vid(t)+c1r1(Pid(t)-Xid(t))+

c2r2(Pgd(t)-Xid(t))

(6)

Xid(t+1)=Xid(t)+Vid(t+1)

高校图书馆的个性化定制学科服务是对现有资源、人力面向用户需求所进行的有效整合与推送，是实现图书馆价值和服务转型的重要途径。具体的服务方式是指学科馆员从分析用户多样化、个性化的需求入手，以丰富的馆藏资源为基础，以专业的服务队伍为依托，以多元的服务渠道为手段，通过嵌入用户研究过程、满足个性化需求来实现图书馆专业化发展的有效途径，能更加体现高校图书馆服务至上、以人为本的服务特点和发展思路。

(7)

式中：t为迭代次数；Pid(t)为第t次迭代时粒子的个体最优解；Pgd(t)为第t次迭代时粒子的全局最优解；c1、c2为学习因子；r1、r2为[0，1]间均匀分布的随机数。

2.2 改进粒子群算法(IPSO)

针对PSO算法容易早熟及后期容易在全局最优解附近产生振荡现象，提出了线性递减权重法，即使惯性权重依照线性从小到大递减，其变化公式为式(8)[10]。

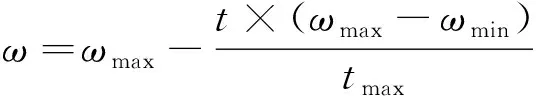
(8)

式中：ωmax为惯性权重最大值；ωmin为惯性权重最小值；t为当前迭代步数。

线性递减权重法的计算步骤如下所述。

1) 随机产生每个粒子的速度和位置。

2) 评价每个粒子的适应度值，将粒子所处的位置及适应度值储存在粒子的个体极值Pbest中，将所有Pbest中最优适应度值的个体位置和适应度值保存在全局极值gbest中。

3) 更新粒子的速度和位置，计算见式(9)和式(10)。

Vi,j(t+1)=ωVi,j(t)+c1r1(Pi,j(t)-Xi,j(t))+

c2r2(Pg,j(t)-Xi,j(t))

(9)

Xi,j(t+1)=Xi,j(t)+Vi,j(t+1),

j=1,2,…,n

(10)

4) 更新权重，计算见式(11)。

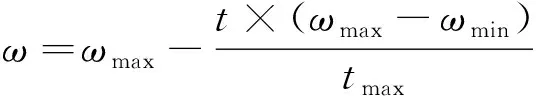
(11)

5) 将每个粒子的适应度值与粒子的最好位置进行对比，如果两者相近，则将当前值作为粒子最好的位置，比较当前所有的Pbest和gbest,更新gbest。

6) 当模型满足条件达到停止时，则停止搜索并输出相应的结果，否则回到步骤3)继续搜索。

2.3 IPSO-ELM模型

IPSO-ELM模型旨在依靠改进的粒子群算法全局搜索能力强、收敛速度快的优点来对极限学习机连接权值和隐含层阈值进行全局寻优，从而提高IPSO-ELM模型的预测精度和预测速度。 具体操作步骤如下所述，IPSO-ELM模型示意图如图2所示。

1) 在选取的35组样本数据中，将前30组作为训练样本，后5组作为测试样本，并将数据做归一化处理。

2) 初始化粒子群参数，并随机产生粒子。

3) 确定ELM网络，设定输入层和隐含层神经元个数，初始化极限学习机输入权值w和阈值b。

4) 计算输出权值，获得均方误差MSE。

5) 将极限学习机训练输出的均方误差作为PSO适应值。

6) 对个体极值Pbest和全局极值gbest初始化，并根据Pbest和gbest更新每个粒子的速度、位置及计算当前粒子对应的适应度值。

7) 将计算所得的粒子群的当前适应度值与先前计算的个体极值Pbest和全局极值gbest进行比较，并更新个体极值和全局极值，最终得到最优粒子的位置。

8) 将获得的最优输入权值w和阈值b赋值给极限学习机，对测试样本进行预测并输出。

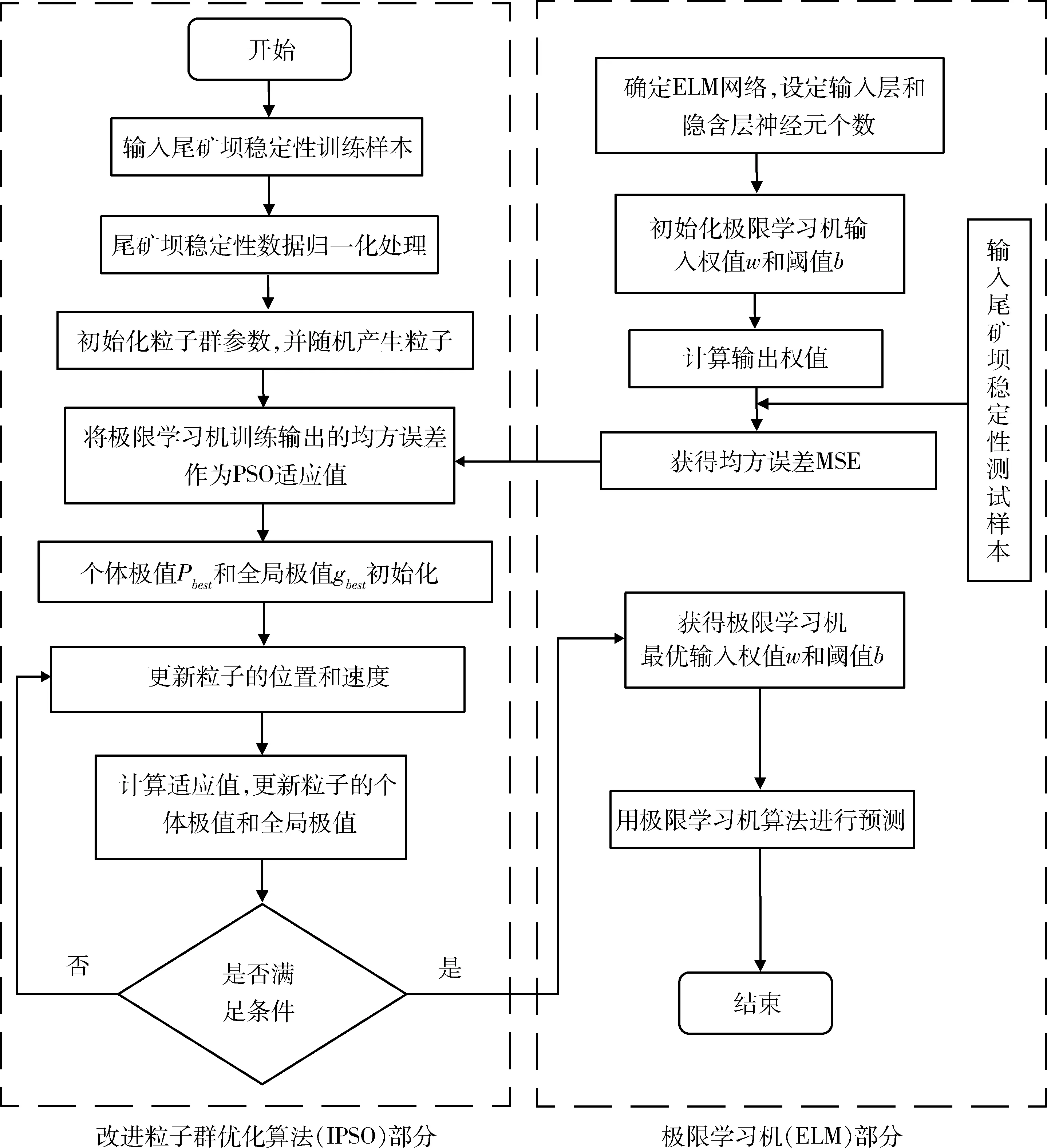
图2 IPSO-ELM模型步骤示意图Fig.2 Schematic diagram of IPSO-ELM algorithm steps

3 实例分析

尾矿坝的稳定性受多种因素影响，其中主要因素有内摩擦角φ、边坡角φ、尾矿坝材料重度γ、孔隙压力比μ、内聚力c和边坡高度H，这些因素共同作用影响着尾矿坝的安全系数F，但安全系数F与影响因素之间存在复杂的关系，传统方法很难做出准确的判断。本文采用IPSO-ELM模型对其进行预测，将6个主要影响因素和安全系数F分别作为模型的输入参数和输出参数。文献[11]选取了具有代表性的35组样本数据，前30组作为训练数据，基于改进的粒子群模型进行参数寻优，后5组作为测试数据，详细数据见表1。

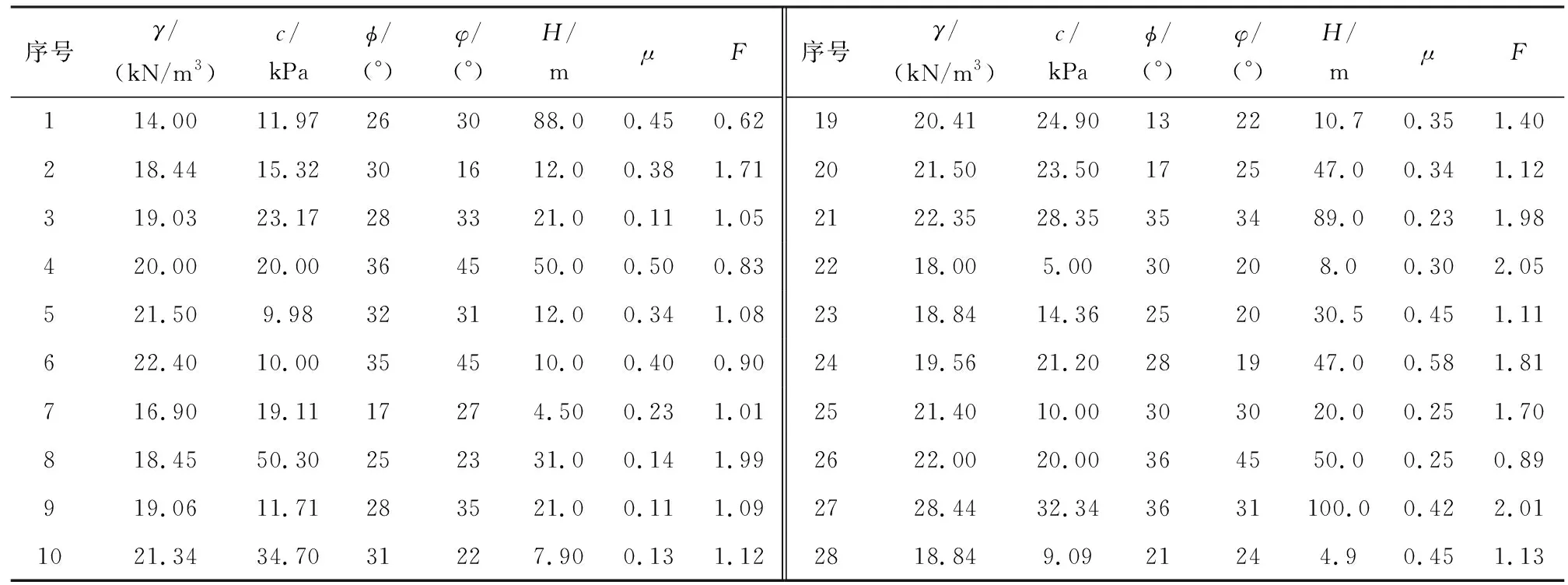
表1 训练数据和测试数据Table 1 Training data and test data

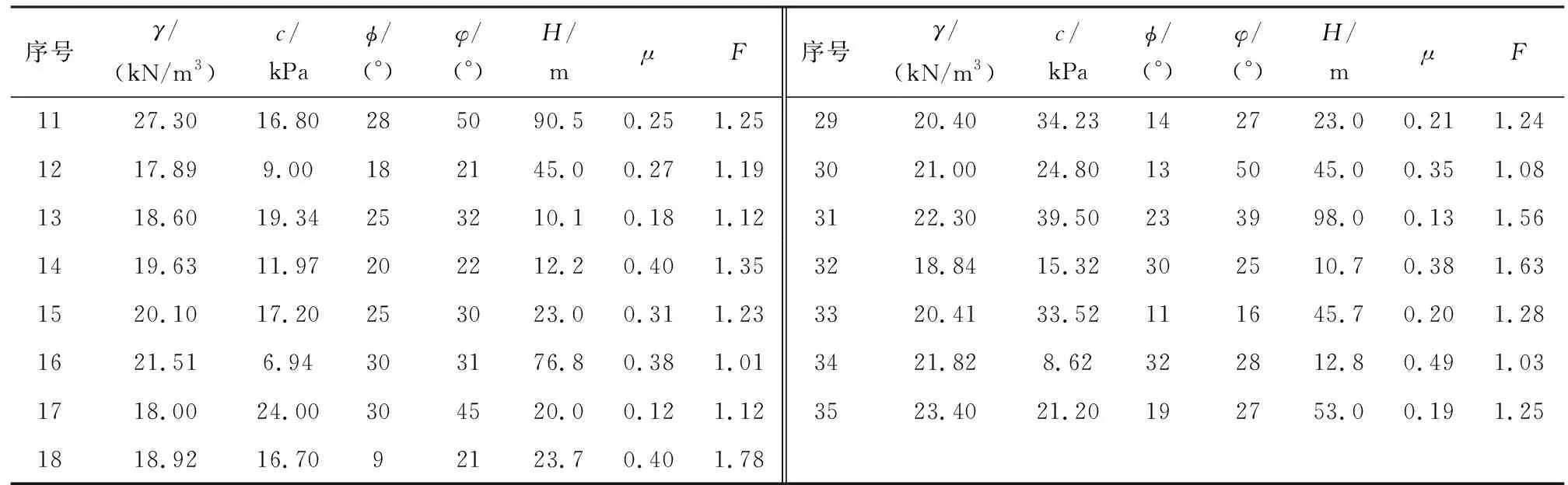
续表1

为了验证IPSO-ELM模型的优越性，将IPSO-ELM模型与单纯的ELM模型和PSO-ELM模型进行对比，如图3所示。由图3可知，IPSO-ELM模型预测精度最高，该模型的预测值逼近于真实值，远远优于ELM模型和PSO-ELM模型，通过对比可知，运用改进的粒子群算法对ELM模型进行优化，可以提高ELM模型的预测精度，达到较好的预测效果。

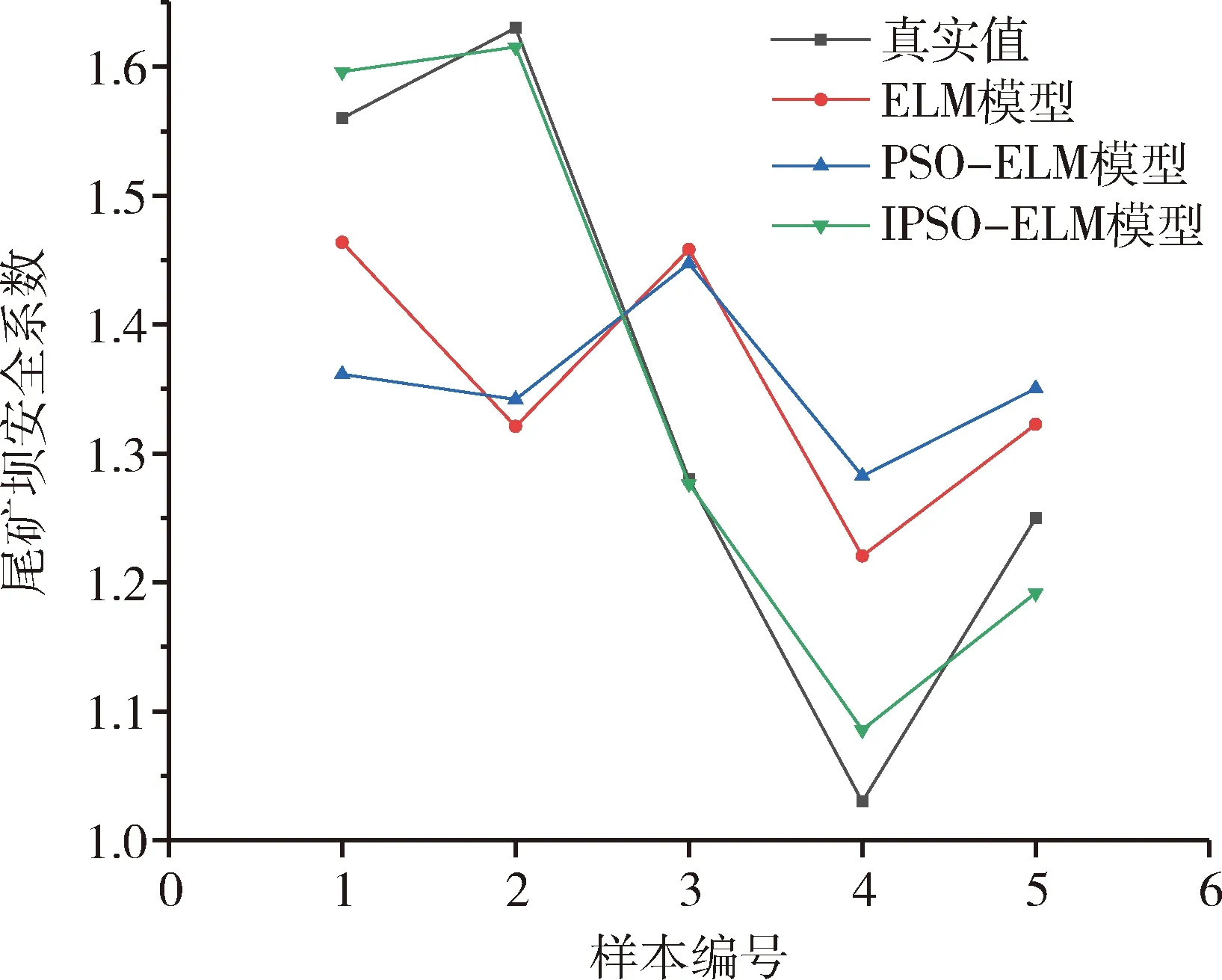
图3 不同模型预测值与真实值对比图Fig.3 Comparison graph of predicted value andtrue value of different models

基于MATLAB软件，运行后可以得出每种模型的均方误差(MSE)，将不同模型的均方误差进行对比，见表2。 由表2可知，ELM模型的均方误差为0.532 67；PSO-ELM模型的均方误差为0.473 55；IPSO-ELM模型的均方误差为0.089 66。由此可以看出，IPSO-ELM模型预测精度高，在尾矿坝稳定性预测中具有一定的可行性和有效性。

表2 不同模型均方误差对比表Table 2 Mean square errors of different models

通过MATLAB软件，设置IPSO-ELM模型和PSO-ELM模型的迭代次数均为100次，将每次迭代误差进行记录并作图对比，如图4所示。由图4可知，IPSO-ELM模型迭代误差随着迭代次数的增加逐次降低，在前20次的迭代过程中误差降低幅度较大，之后误差降低幅度缩减，但是一直处于误差降低状态，说明IPSO-ELM模型寻优效果比较理想；而PSO-ELM模型在迭代16次以后，迭代误差不再变化，其值稳定为0.145 63，说明该预测模型预测效果不理想，预测误差较大。

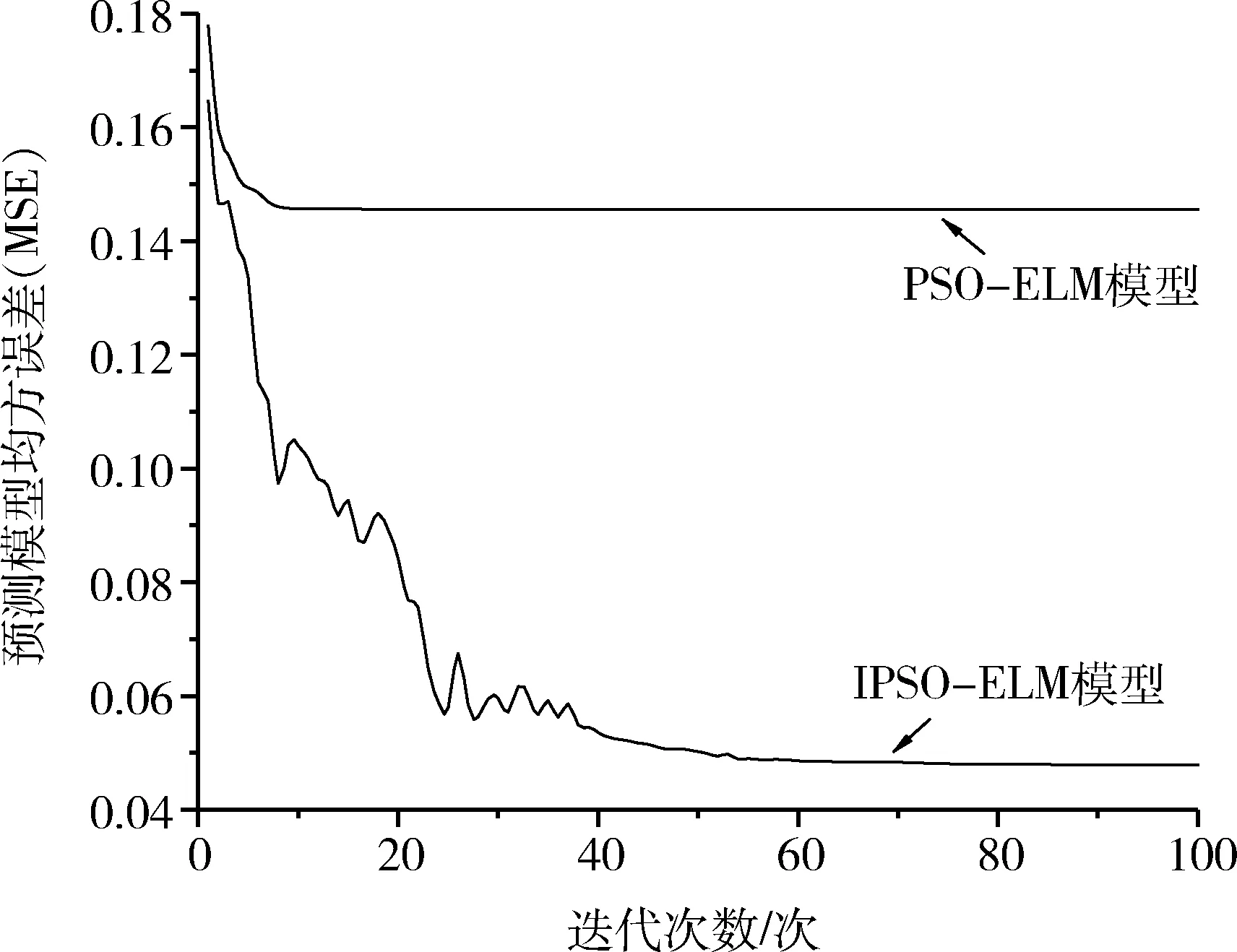
图4 不同模型迭代100次误差变化图Fig.4 Error change diagram of 100 iterationsfor different models

不同模型预测结果相对误差对比见表3。 由表3可知，ELM模型预测结果最大相对误差为24.02%，平均相对误差为16.17%；PSO-ELM模型预测结果最大相对误差为24.51%，平均相对误差为15.20%；IPSO-ELM模型预测结果最大相对误差为5.41%，平均相对误差为2.71%。 由此可以看出，IPSO-ELM模型有较高的预测精度，预测结果较为稳定，预测值与真实值误差较小，模型构建合理，适用性较强。

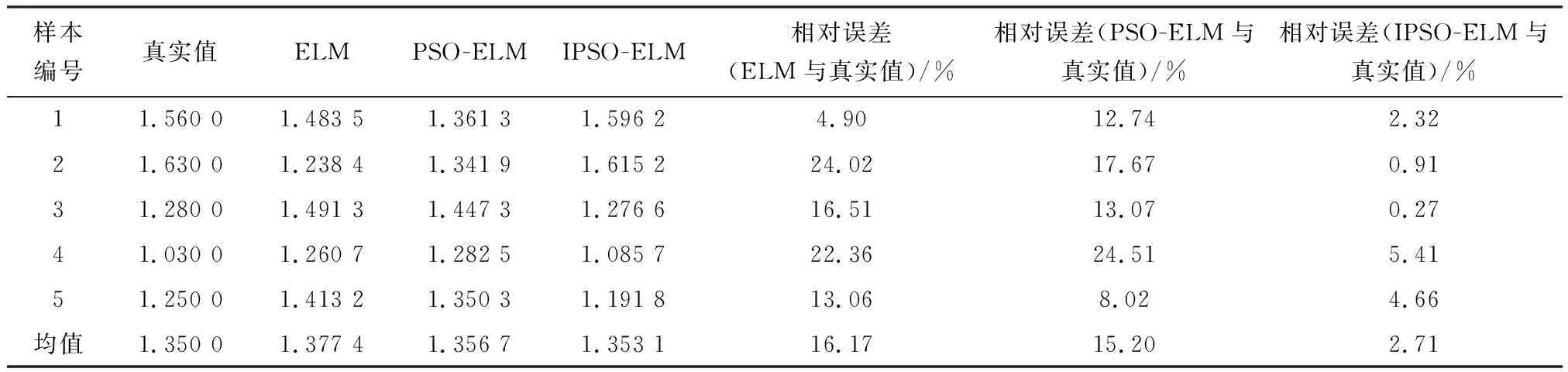
表3 不同模型预测结果相对误差表Table 3 Relative errors of prediction results of different models

4 结 论

1) 在PSO-ELM模型的基础上，引入线性递减权重法，旨在改进PSO全局搜索能力、收敛速度来对极限学习机连接权值和隐含层阈值进行全局寻优，进而提出一种IPSO-ELM模型用于尾矿坝稳定性分析。

2) 通过3种模型的预测结果与实际值对比，结果表明，IPSO-ELM模型相较于单纯的ELM模型和PSO-ELM模型，其仿真均方误差和相对误差明显较小，有较高的泛化能力和预测精度。

3) 提出的改进粒子群算法优化极限学习机(IPSO-ELM)模型能够通过对已有数据进行训练，预测尾矿坝的安全系数，为尾矿坝的稳定性评判提供依据，可以广泛应用于尾矿坝稳定性分析等实际工程中。