基于二维Gabor小波和孪生支持向量机的图像识别算法
吕 洁,麦雄发,谢 妙
(1.玉林师范学院 计算机科学与工程学院,广西 玉林 537000;2.南宁师范大学 数学与统计学院,广西 南宁 530001)
图像数据作为重要的数据存储方式,其识别性能影响其在多个领域应用的适用性。图像数据相比较于文本,其维度和数据量都较大,因此如何从图像中提取关键的特征及纹理对于图像识别研究具有重要意义。将图像中的高维图像特征进行分割提取,并通过有效滤波获得图像的大致纹理,通过对纹理特征的分析来区分不同的图像样本,从而实现图像样本的准确识别。在图像识别过程中,图像样本的特征提取、图像特征的维度分解及图像特征的分类成为图像识别的研究热点[1],通过这三方面的协同优化来促使图像识别能够获得更高的性能。
关于图像识别的研究较多,远攀等[2]详细对比了各种深度学习算法在图像识别中的适用性及优缺点;胡龙辉等[3]采用广泛生成对抗网络算法进行图像特征分类识别,识别准确率较高但对复杂环境的图像纹理识别效率低;孙平安等[4]采用卷积神经网络算法进行图像识别,通过特征的卷积运算有效提高的复杂图像的识别性能。Gabor小波变换作为一种较为先进的特征提取技术,可以较好地分析局部时频域所蕴含的信息,从而更加准确地分析信号的高低频域特性。
本文尝试采用二维Gabor小波进行图像纹理特征提取,实现更加有效的图像关键纹理提取。结合局部线性嵌入(Locally linear embedding,LLE)完成特征降维,在一定程度上缓解特征冗余和高维特征运算的效率问题。然后,采用孪生支持向量机(Twin support vector machine,TWSVM)来进行图像分类识别,证实TWSVM分类器在提高高维图像样本的识别准确率方面的性能。
1 图像识别框架
首先,通过对待识别的图像样本进行分块,提取每一块图像特征并进行Gabor滤波,设置滤波的尺度和方向,接着采用LLE进行特征降维,最后采用TWSVM对降维后的特征进行分类,如图1所示。
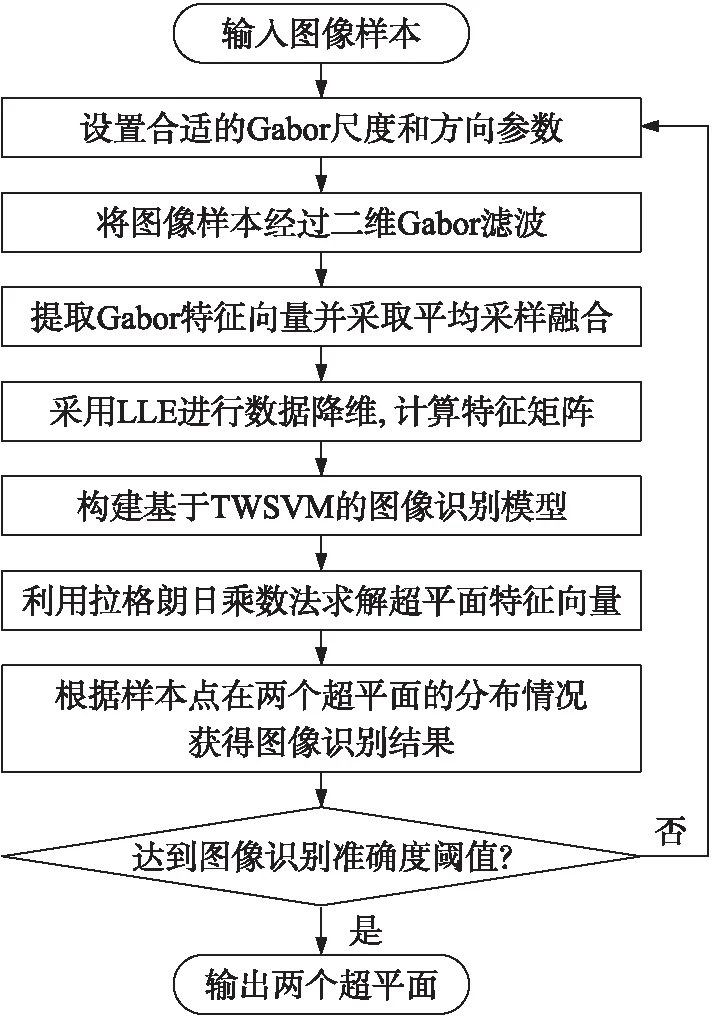
图1 图像识别流程
2 图像特征的提取与降维
2.1 二维Gabor小波特征提取
二维Gabor小波作为图像尺度表示和特征分析的常用工具,可以方便实现图像的尺度变化。对于灰度图像z=(x,y),其滤波器表达式[5]为
(1)

将式(1)按实部与虚部进行拆分得[7]
(2)
[sin(iku,v)]
(3)
进行二维Gabor小波时,为了获取全面图像数据而不丢失,需要合理设置二维Gabor小波主要参数u、v和σ。
2.2 LLE降维
经过Gabor滤波后得到的图像特征的维数较高,考虑到特征冗余和高维特征运算及存储的效率问题,有必要对图像特征进行有效降维。下面对LLE降维进行数学描述。对m个样本点实现降维,设样本xi可以由其相邻样本xj、xk和xl经过线性运算得[8]
xi=ωijxj+ωikxk+ωilxl
(4)
式中:ωij、ωik和ωil分别为样本xi和其相邻样本xj、xk和xl的线性系数。
在实际操作过程中,xi的相邻样本选择可以多个,设xi的k个邻居样本组成的集合为Qi,为了保持降维后样本点仍属以前的线性关系,其目标函数为[9]
(5)
设Cjk=(xi-xj)T(xi-xk),则
(6)
式中:Cls=(xi-xl)T(xi-xs)。
LLE能够保持降维过程中ωij保持不变,所以根据ωij,可以求解降维后的样本集合[10]。
(7)
式中:zi为xi经过降维后的值,通过求解ωij的特征值所对应的特征向量则可以得到降维后的集合Z,Z=[z1,z2,…zm]。
3 孪生支持向量机的图像识别
TWSVM采用2个超平面进行分类,两类样本个数分别为m1和m2,维度均为n,TWSVM的两个超平面的数学表示为[11]
xTw(1)+b(1)=0xTw(2)+b(2)=0
(8)
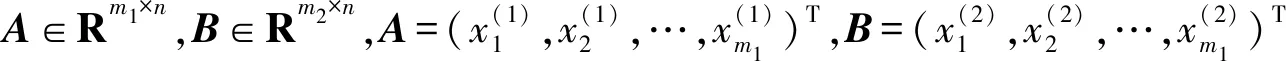
TWSVM1:
s.t. -(Bw(1)+e2b(1))+ξ≥e2
ξ≥0
(9)
TWSVM2:
s.t. -(Aw(2)+e1b(2))+η≥e1
η≥0
(10)
式中:ξ和η为非负常量,e1=(1,1,…,1)T∈Rm1,e2=(1,1,…,1)T∈Rm2,c1和c2常量。
构建拉格朗日乘子,计算式(9),得
e2b(1))+ξ-e2)-βTξ
(11)
式中:α=(α1,α2,…,αm2)T,β=(β1,β2,…,βm2)T,两个向量分别为两个拉格朗日参数变量集合。
式(7)分别对w(1)、b(1)和ξ求偏导,且令等式为0,可得[13]
AT(Aw(1)+e2b(1))+βTα=0
(12)
(13)
c1e2-α-β=0
(14)
联合式(9)和(10)得
(15)

HTHu+GTα=0
(16)
则u=-(HTH)-1GTα。
由于u=[w(1)b(1)]T,那么求得u后可以求得w(1)和b(1),获得超平面xTw(1)+b(1)=0。根据同样的方法可以获得另外一个超平面xTw(2)+b(2)=0。
首先,对二维Gabor小波的尺度和方向参数进行差异化设置,验证不同参数下的图像识别性能。其次,分别对比SVM和TWSVM的性能差异,验证TWSVM在图像识别分类中的差异性。最后,对常见图像识别算法和本文算法进行对比,验证不同算法的图像识别差异性。
4 实例仿真
为了验证二维Gabor小波和TWSVM对图像识别的性能,进行实例仿真。为了充分验证Gabor+LLE+TWSVM在图像识别中的性能,分别选择了表1所示的ORL人脸数据库、CASIA WebFace数据库和dogs_vs_cats数据库3个数据来源作为本文仿真对象,训练和测试比例均按照3∶1分配。
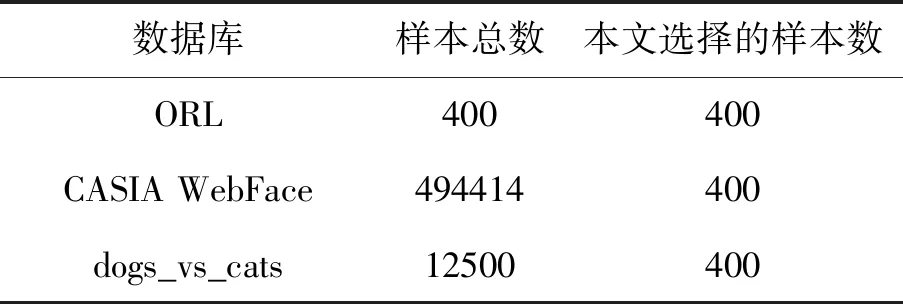
表1 仿真数据库
4.1 二维Gabor的u,v参数对图像识别的性能影响
采用Gabor+LLE+TWSVM算法分别对表1中的3个库样本进行性能仿真。为了验证二维Gabor小波纹理提取对图像识别性能的影响,分别差异化设置二维Gabor小波的尺度和方向变量,验证对3个图像库的识别准确率性能,结果如表2~表4所示。

表2 不同u,v参数对应的识别率(ORL库)
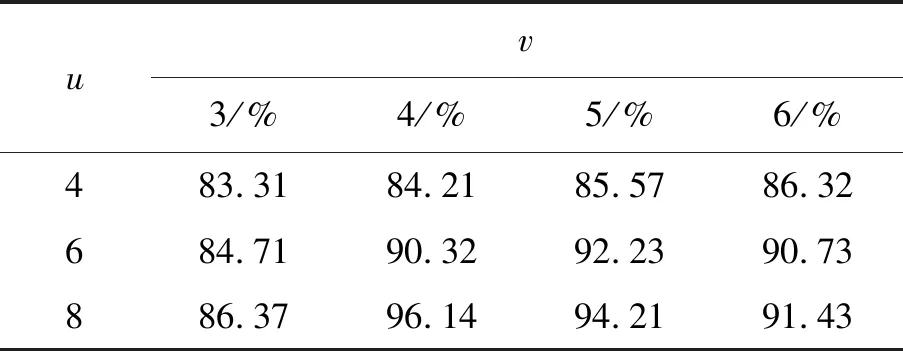
表3 不同u,v参数对应的识别率(CASIA WebFace库)
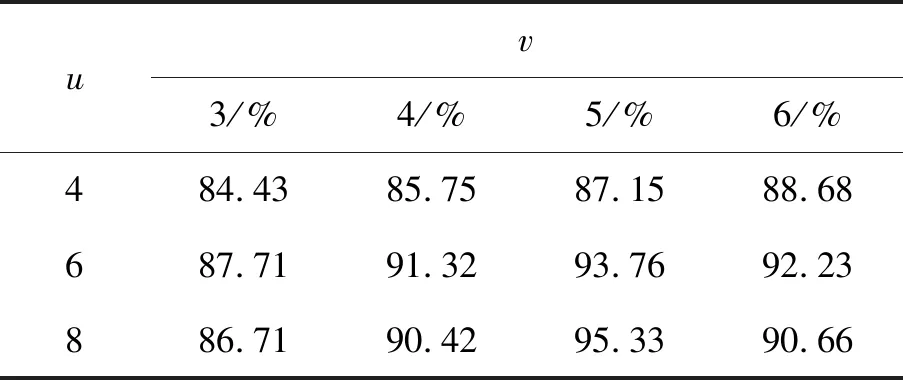
表4 不同u,v参数对应的识别率(dogs_vs_cats库)
从上述3个表可知,不同二维Gabor小波参数对3种不同样本的图像识别率影响显著,ORL库在v=5,u=8时获得了最优识别率98.29%,CASIA WebFace库在v=4,u=8时获得了最优识别率96.14%,dogs_vs_cats库在v=5,u=8时获得了最优识别率95.33%,因此不同的库在进行识别时应选取适合的v和u参数,这3种图像样本的尺寸各异,在分割时模块大小和维度有差异,在进行二维Gabor小波滤波时的尺寸和方向需要灵活选择,否则可能提取图像纹理时造成与原图像误差较大,不能体现二维Gabor小波在图像处理关键纹理提取中的优势。
4.2 TWSVM与SVM的识别性能比较
根据4.1节,选择合适的二维Gabor小波u和v参数进行纹理提取并进行LLE降维,图像识别分类器分别选择SVM和TWSVM方法,验证两种不同分类器对图像识别性能影响。
从表5可知,TWSVM在3种不同图像集的识别性能均优于SVM,在ORL集中TWSVM比SVM提高了3.84%,在CASIA WebFace集中提高了4.87%,在dogs_vs_cats 集中提高了4.66%。下面对3种算法的RMSE性能进行仿真,结果如图2、3和4所示。

表5 TWSVM与SVM的图像识别性能
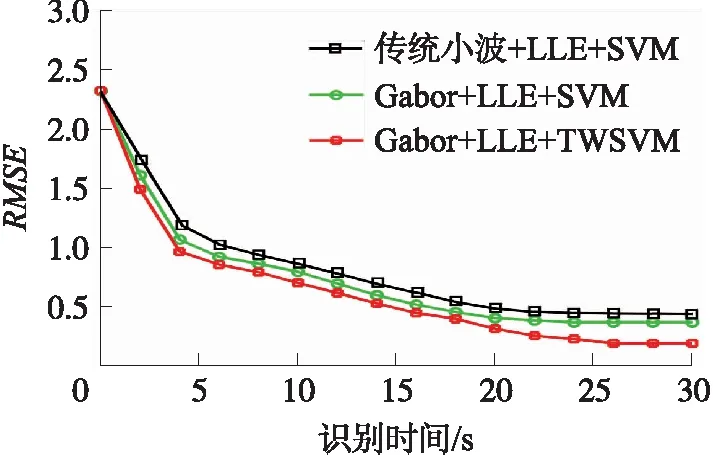
图2 识别准确率的RMSE性能(ORL集)
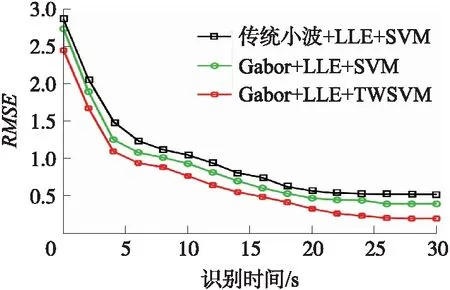
图3 识别准确率的RMSE性能(CASIA WebFace集)
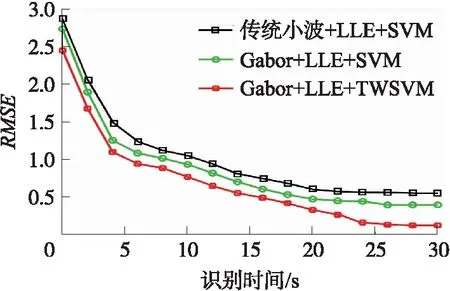
图4 识别准确率的RMSE性能(dogs_vs_cats集)
在ORL集中,Gabor+LLE+TWSVM获得了低于0.2的RMSE性能,算法在26 s获得了稳定的RMSE值,而Gabor+LLE+SVM在训练过程中的RMSE性能均不如本文算法,在20 s之前,2种算法的RMSE性能差距较小,但20 s后两者RMSE值逐渐拉开,Gabor+LLE+SVM在24 s达到收敛,而本文算法在26 s达到收敛,且本文算法收敛时RMSE更小;在CASIA WebFace集中,从5 s之后,两者的RMSE值呈现较大差距,两者均在26 s开始收敛,Gabor+LLE+SVM的RMSE值收敛于0.5左右,而Gabor+LLE+TWSVM约收敛于0.25;在dogs_vs_cats集中,Gabor+LLE+SVM和Gabor+LLE+TWSVM分别在26 s和28 s开始收敛,收敛值分别为0.5和0.2。综合而言,在RMSE收敛值方面,采用TWSVM分类器比SVM分类器图像识别效果更好,识别时间方面两者相差较近。
4.3 常见识别算法的性能
为了进一步验证Gabor+LLE+TWSVM算法在3种图像集中的识别性能,分别采用神经网络(NN)[14]算法、Adaboost[15]算法、卷积神经网络(CNN)[16]算法和Gabor+LLE+TWSVM算法进行图像识别,其仿真性能如图5~7所示。
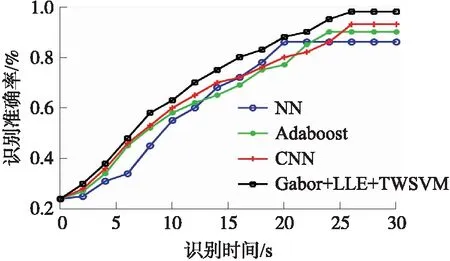
图5 4种算法的识别准确率(ORL集)

图6 4种算法的识别准确率(CASIA WebFace集)

图7 4种算法的识别准确率(dogs_vs_cats集)
在3种不同数据集中,Gabor+LLE+TWSVM算法均表现出了最高的识别准确率,对于3种不同数据集的识别准确率均高于0.95,CNN算法次之,NN算法最差;在图像识别效率方面,NN算法最好,其他3种算法差距不大。本文算法因为滤波和降维增加了图像识别的时间,但却获得了更高的图像识别准确率,但对比其他2种分类准确率较高的算法,本文算法的识别时间与其他2种算法相差较小。
综上所述,本文采用二维Gabor小波进行图像纹理提取,通过LLE降维后获得待识别的图像样本,这样有效提高了图像识别效率,最后采用TWSVM进行分类识别。合理设置二维Gabor小波尺度和方向参数可以获得图像的关键纹理,经过TWSVM分类后可以获得较好的图像识别准确率,后续研究将从二维Gabor小波参数优化和TWSVM的多种激励函数方面展开研究,以进一步提高Gabor+LLE+TWSVM在图像识别方面的适用度。

