经历统计过程 感受统计之趣
文/万广磊
统计学是一门古老的科学,与我们的生活息息相关。同学们打开电视、报纸、杂志、互联网等,经常会看到各种各样的统计图表,从而了解周围世界。根据需要,我们也会选择一些统计图表,对其中的数据来源、描述数据的方法、得出的结论等进行分析,以便做出合理的决策。
一、利用数据解决问题
利用数据解决简单问题的过程如下:

在实际生活中,我们会发现一些问题亟待解决。于是,我们设计调查问卷或者直接调查,收集相关信息,然后整理得到有效数据,用常用的统计图表描述数据,多角度分析数据,最后,提出方案,解决问题。
二、合理选择调查方式
统计调查有普查和抽样调查两种方式。
普查通过调查总体中的每个个体来收集数据,得到的调查结果比较准确,但所费人力、物力和时间较多;抽样调查通过调查样本中的每个个体来收集数据,得到的调查结果不够准确,但是接近准确结果,所费人力、物力和时间较少。我们要根据不同的情况选择合适的调查方式。
比如,调查长江的水质、全国中学生的视力情况、某省居民的网上购物情况、某个节目的收视率等,因为调查范围广,适合采用抽样调查方式;而调查某班级学生的身高、体重、阅读的课外书数量、喜欢的体育活动等,适合采用普查方式。
三、正确理解统计概念
要学好统计方法,首先要理解这几个概念:总体、个体、样本、样本容量。
总体是指考察对象的全体;个体是总体中的每一个考察对象;样本是总体中所抽取的一部分个体;而样本容量则是指样本中个体的数目,注意没有单位。
比如,2021 年某市有近56000 名考生参加中考,为了调查这些考生的数学成绩,从中随机抽取3000名考生的数学成绩进行统计分析。其中,3000名考生的数学成绩是总体的一个样本,每名考生的数学成绩是个体,近56000名考生的数学成绩是总体,3000是样本容量。
四、选取代表性样本
在统计中,我们通常从总体中抽取样本,通过样本估计总体。为了使估计、推断的总体特性更加准确,抽样时要注意样本的代表性。
比如,要了解全校学生的课外作业负担情况,比较有代表性的样本是七、八、九三个年级各10%的学生或者七、八、九三个年级各班学号尾数为4 的学生,而不是七、八、九三个年级(1)班的学生或者全校的女生。
五、学会绘制统计图表
我们可以利用统计图表整理、描述数据,了解数据的分布特征和变化规律,从数据中获取信息、做出决策。常见的统计图表有扇形统计图、条形统计图、折线统计图、频数分布表。不同的统计图表有不同的特点,比如,扇形统计图描述了由数据所表现出来的部分与整体的关系;折线统计图描述了数据的变化过程与趋势;条形统计图用宽度相等的“条形”的高度描述各个统计项目的频数。随着计算机技术和统计学的不断发展,现在还出现了很多新颖、有趣的统计图表。
六、通过样本估计总体
我们可以根据统计图表提供的信息进行分析,利用样本的某种特性估计总体的相应特性,再做出合理的决策。
比如,我国古代数学名著《九章算术》中有一个“米谷粒分”的问题:粮仓开仓收粮,有人送来米1534 石,为检验米内夹谷多少,抽样取米一把,数得254 粒内夹谷28 粒,则这批米内夹谷约为多少?求这批米内夹谷多少,用的就是样本估计总体的思想。
一些益智类节目或竞赛活动也会有类似的有趣问题。比如,某市的一次科普知识竞赛中,有一道满分为8 分的解答题,按评分标准,所有选手的得分只有四种情况:0 分,3 分,5分,8分。为了了解学生的得分情况与题目的难易情况,从全市8000名选手的试卷中随机抽取一部分,通过分析与整理,绘制了下面的统计图。
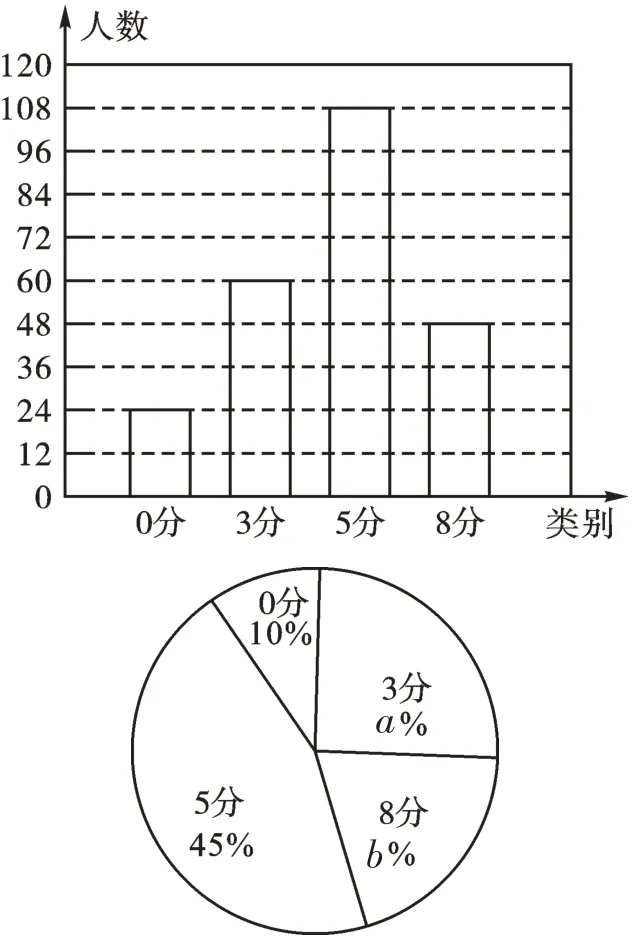
得分情况统计图
根据以上信息,我们可以估计该地区得满分(即8 分)的学生有1600 人。如果已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7 时,此题为中等难度试题;当0.7<L<1 时,此题为容易题。通过 计 算,X=0×10%+3×25%+5×45%+8×20%=4.6,L==0.575,结合难度系数,0.4<0.575≤0.7,所以此题为中等难度试题。

