基于信噪比的MEMS压力传感器设计与分析
冒晓莉,吴其宇,张加宏,2,李 敏,赵雪伟
(1.南京信息工程大学电子与信息工程学院,江苏南京 210044;2.南京信息工程大学,江苏省大气环境与装备技术协同创新中心,江苏南京 210044)
0 引言
MEMS压阻式压力传感器以其小体积、低成本、高性能等优势,被广泛应用于电器制造、汽车工业、生物医疗、气象观测以及航空航天等各项领域[1]。MEMS压阻式压力传感器的研究主要集中在传感器灵敏度、线性度以及量程等几个方面[2-4],随着测量要求的提升,对传感器的分辨率提出了更高的要求。噪声的大小决定了传感器的最小可检测信号,这是影响压力传感器性能的重要因素之一[5-7]。
为了探究MEMS压力传感器压敏电阻结构对信噪比的影响,本文进行了基于MEMS硅压阻式压力传感器结构的设计和分析[8-9]。首先使用ANSYS仿真,探究各结构传感器加压下的应力分布,通过仿真数据计算得到各结构的传感器噪声与信噪比。随后使用SOI(绝缘体上硅)制作部分传感器芯片,通过部分刻蚀SOI硅膜引入了凸起的压敏电阻形成惠斯登电桥结构,比较输出信号的噪声和信噪比,从而论证仿真理论分析的正确性,得到传感器噪声、信噪比与其结构的关系。本文研究结果对高信噪比MEMS压阻式压力传感器的结构设计具有一定参考价值。
1 MEMS传感器结构设计与模拟仿真
1.1 MEMS传感器结构设计
本文提出的MEMS压阻式压力传感器结构如图1所示。为提高传感器的灵敏度,采用SOI硅片制作了凸起的传感器压敏电阻结构。传感器有不同电阻长度l、折叠条数n的各种压敏电阻结构,如U型、N型、W型、以及VW型。图1为单条型压敏电阻组成的传感器,凸起的压敏电阻R1和R2、R3和R4两两对称,形成惠斯登电桥,相对位置的铝盘同为输入端或输出端,通电下传感器将外加压力信号转化为电压值输出。
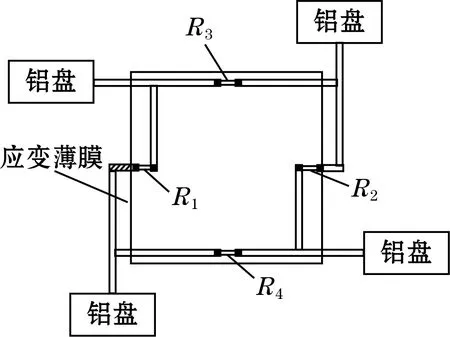
图1 MEMS硅压阻式压力传感器结构
压敏电阻阻值在应力作用下发生变化,由于应变效应引起的电阻率变化远小于压阻效应带来的电阻率变化[10],其阻值变化率可近似表示为
(1)
式中:R为初始电阻;ΔR为应力作用下电阻阻值变化量;ρ为电阻率;Δρ为电阻率变化量;π为压阻系数;σ为应力。
本文的P型压敏电阻的掺杂浓度为1017cm-3,对应的电阻率约0.202 Ω·cm。
因为在μm厚度的应变薄膜上,压阻条受到的剪切向应力很小,所以式(1)可化为

(2)
式中:πl与πt分别为纵向、横向压阻系数,πl=73.5×10-11Pa-1,πt=-67.8×10-11Pa-1;σl与σt为对应纵向、横向应力。
理想条件下,各电阻初始阻值、对称位置电阻阻值变化率相等,R1=R2=R3=R4=R,ΔR1=ΔR2,ΔR3=ΔR4,以左下角和右上角铝盘为输入端,左上角和右下角铝盘为输出端,在输入电压Vin条件下,输出电压Vout可表示为
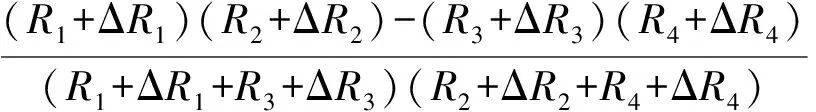
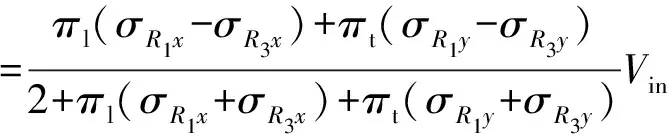
(3)
式中σR1x、σR1y、σR3x、σR3y分别为图1中电阻R1、R3在x、y方向上的应力。
为保证传感器输出信号的线性度与灵敏度,需要选择合适的膜片厚度。膜片过厚会降低灵敏度,过薄会降低线性度与抗负载能力。考虑到加工工艺水平,本文选取膜片厚度h为20 μm。在0~300 kPa满量程范围内,传感器膜片边长a和厚度h需满足下式:
(4)
式中:P为外加气压大小;E为硅的弹性模量,E=170 GPa;v为泊松比,v=0.278。
根据式(4)计算可得弹性方形敏感膜片的长度a≤1 184 μm,本文选取的膜片边长为900 μm。本文制作传感器使用SOI硅衬,厚度650 μm,根据湿法腐蚀角度为57.74°,计算得C型硅杯窗口的大小为1 792 μm,选取的传感器芯片尺寸为3 000 μm×3 000 μm。
1.2 有限元建模与仿真分析
为研究各结构设计的可行性与输出变化,利用ANSYS有限元分析软件对各结构MEMS压阻式压力传感器进行建模与仿真分析。在本文中压敏电阻材料为掺硼硅,厚度为4.5 μm,表面覆盖了一层同样结构的1 μm厚二氧化硅保护层。压敏电阻结构下方为1 μm的绝缘二氧化硅层,20 μm的应变薄膜,底层为硅杯,硅杯底部与玻璃基底通过阳极键合。
图2给出了外加100 kPa压力、不引入电阻的薄膜应变情况,σx和σy分别为x、y方向上的应力。图2表明应变薄膜边缘中央应力最大,故一般优先将压敏电阻放置在此。图3为引入长度50 μm的单条型电阻后应力分布。
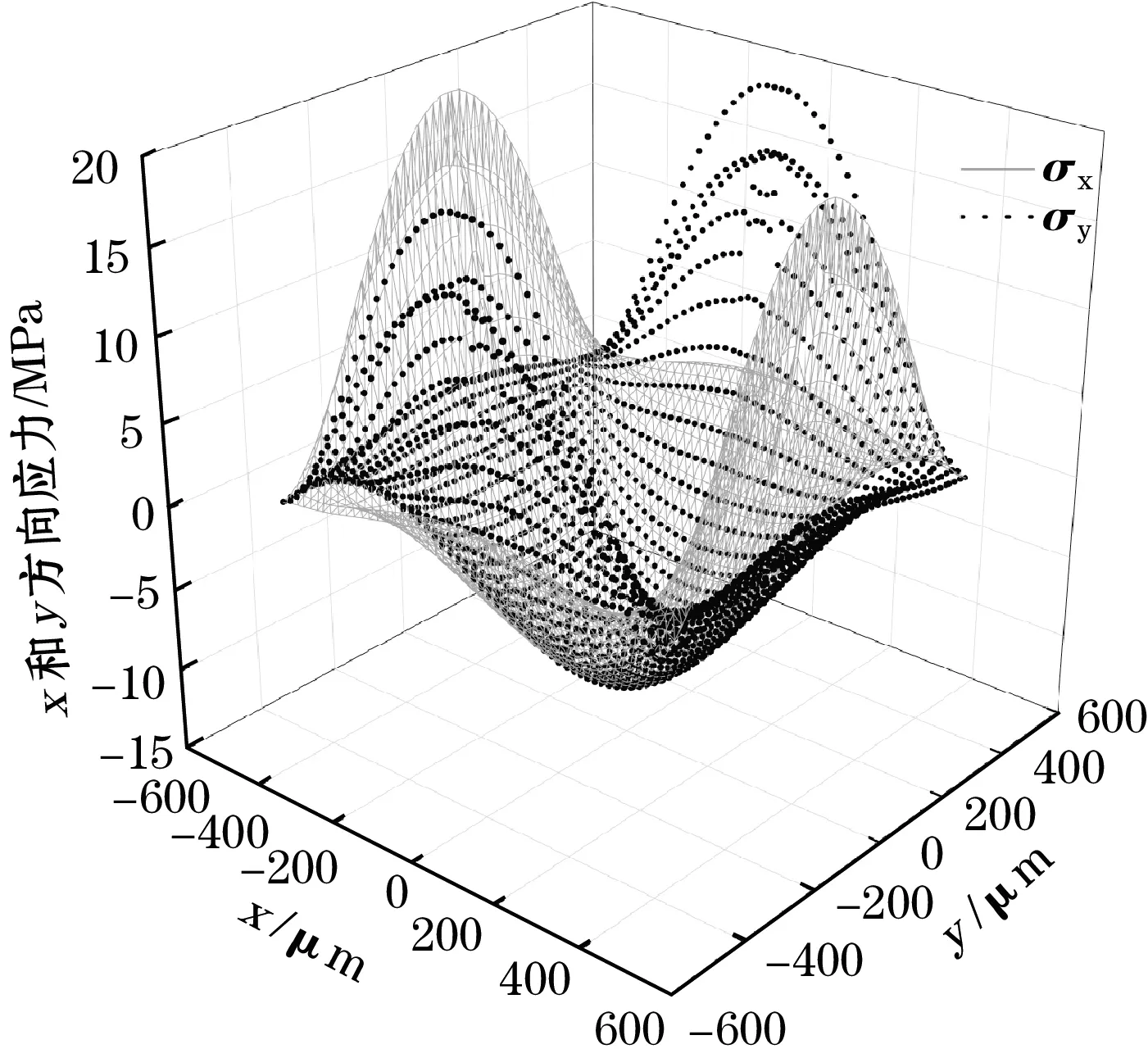
图2 薄膜应力分布
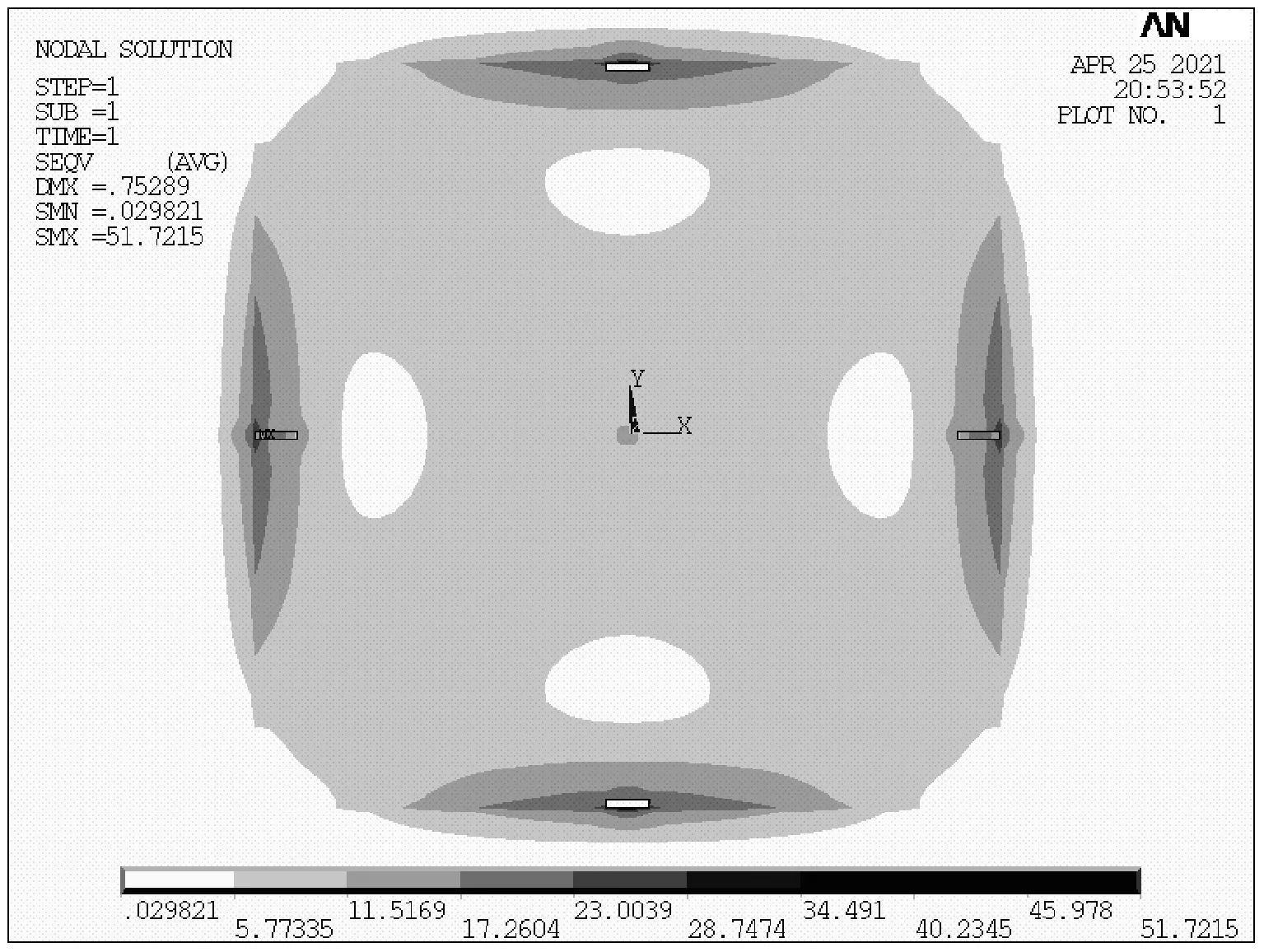
图3 引入电阻后应力分布
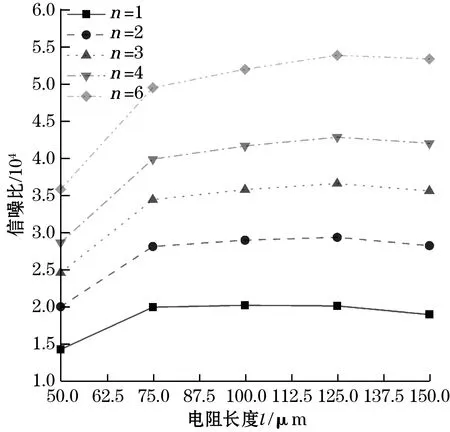
根据图2、图3中应力分布,设计不同长度l、折叠数目n的压敏电阻结构并依次仿真,l、n由边缘中央向薄膜中央和两侧进行增长。结合式(3)得100 kPa、6 V输入下传感器输出与电阻结构n、l的仿真拟合关系曲线,如图4所示。由图4可知,Vout与传感器结构有关,随l的增大先升后降,75 μm左右时出现极大值;当l足够长时,Vout随n增大而增加。

图4 Vout与n、l的关系
2 传感器噪声与信噪比分析
2.1 传感器噪声分析
压力传感器噪声构成复杂,主要由热噪声、闪烁噪声组成。噪声总的功率谱密度可以视为各噪声功率谱密度之和:
(5)

热噪声又称电阻噪声,是由压敏电阻中电荷载流子由于随机运动产生的,表现形式近似于白噪声。热噪声的功率谱密度与温度有关,与电阻所加电压频率无关。其表达式为
(6)
式中:波尔兹曼常数K=1.38×10-23J/K;温度T=300 K;R为电阻阻值;ρ为电阻率;w为电阻宽度,w=10 μm;t为电阻厚度,t=4.5 μm。
闪烁噪声由器件的局部起伏引起发射电子缓慢起伏导致,其功率谱密度与频率成反比,通常出现在低频范围,计算公式为
(7)
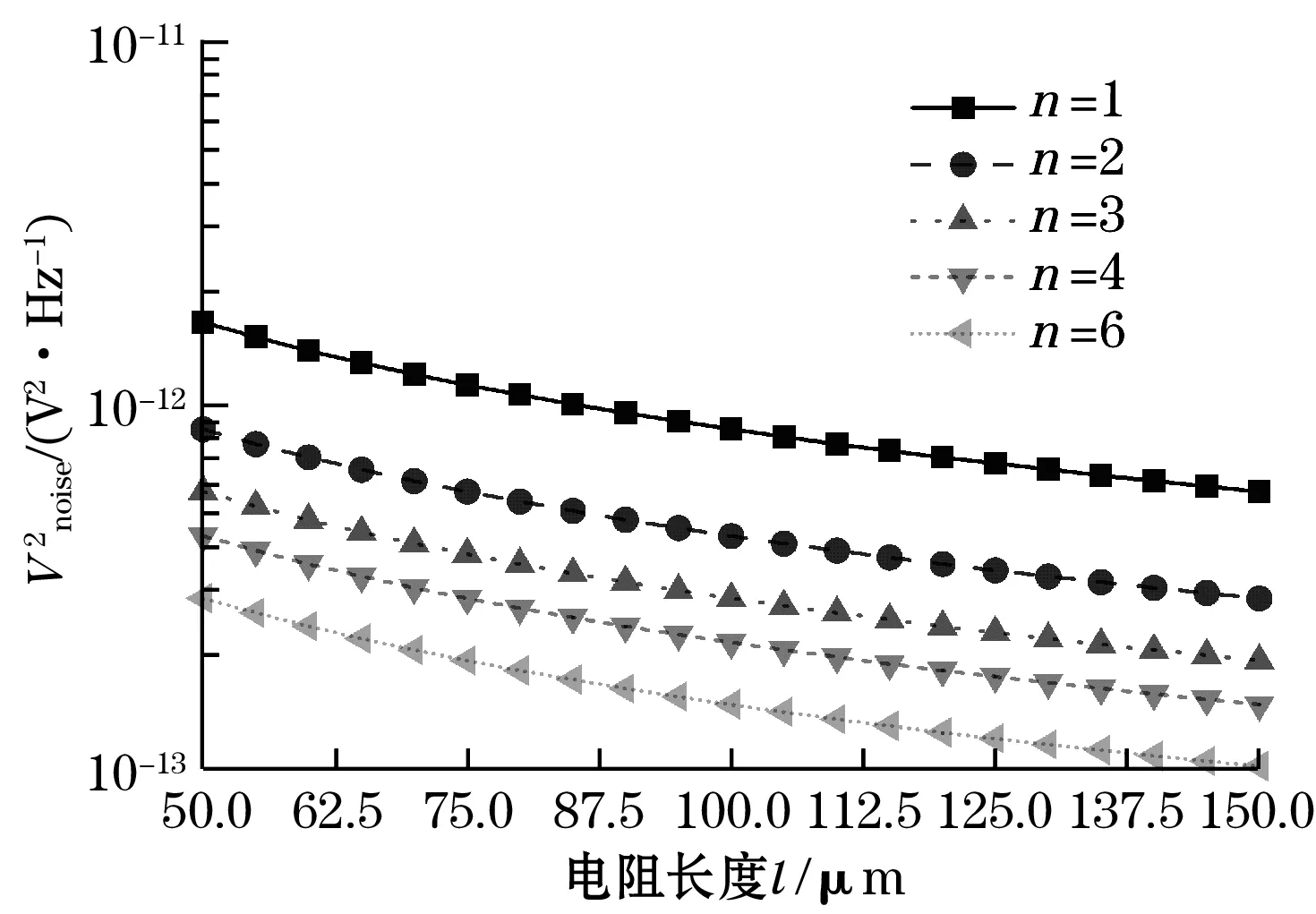
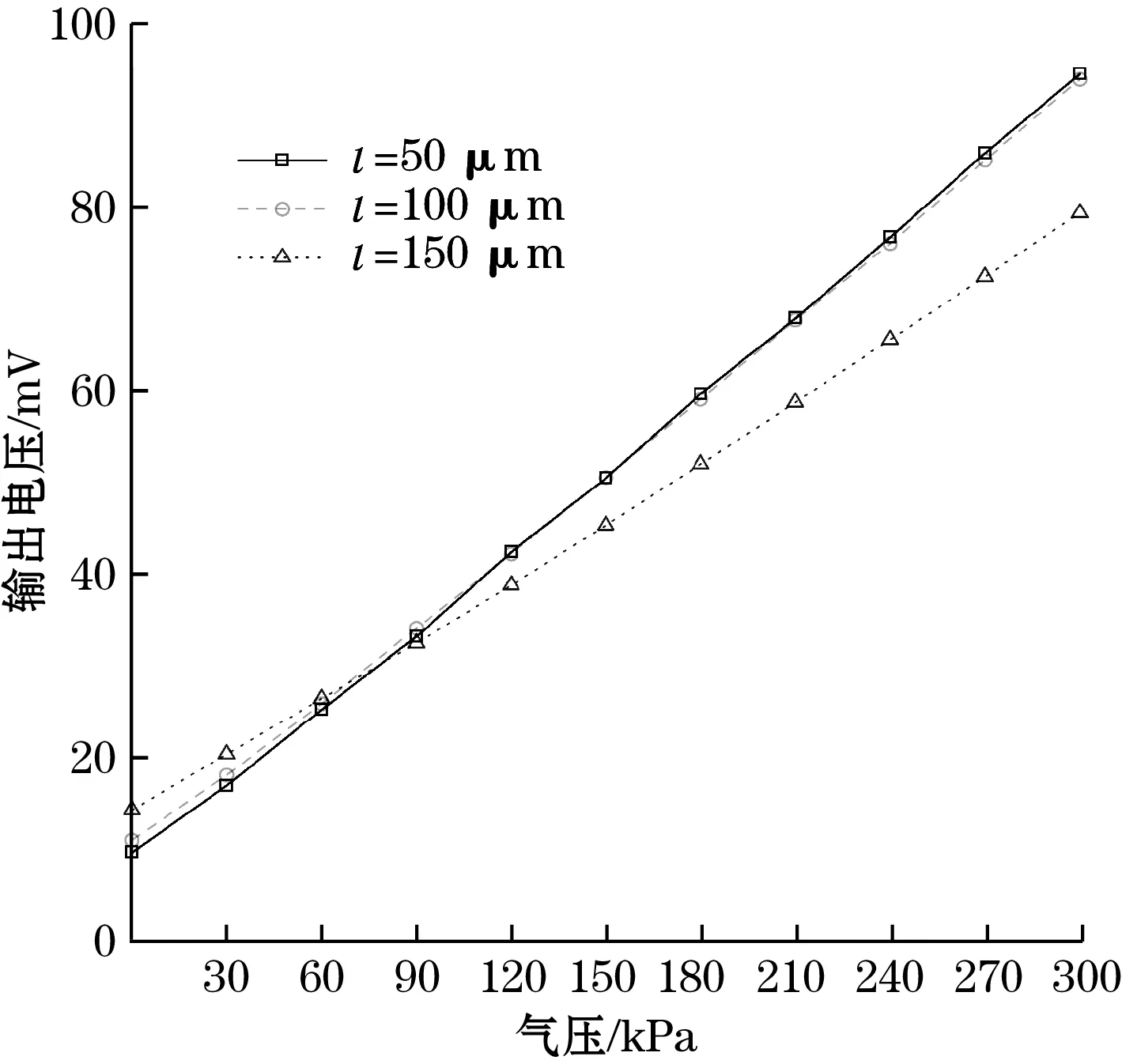
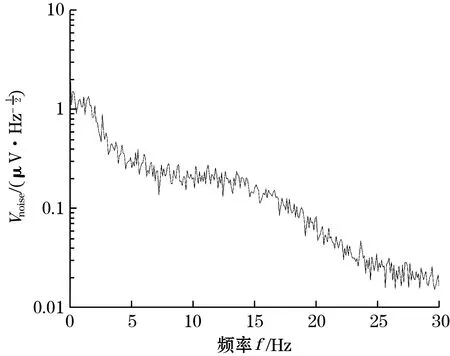
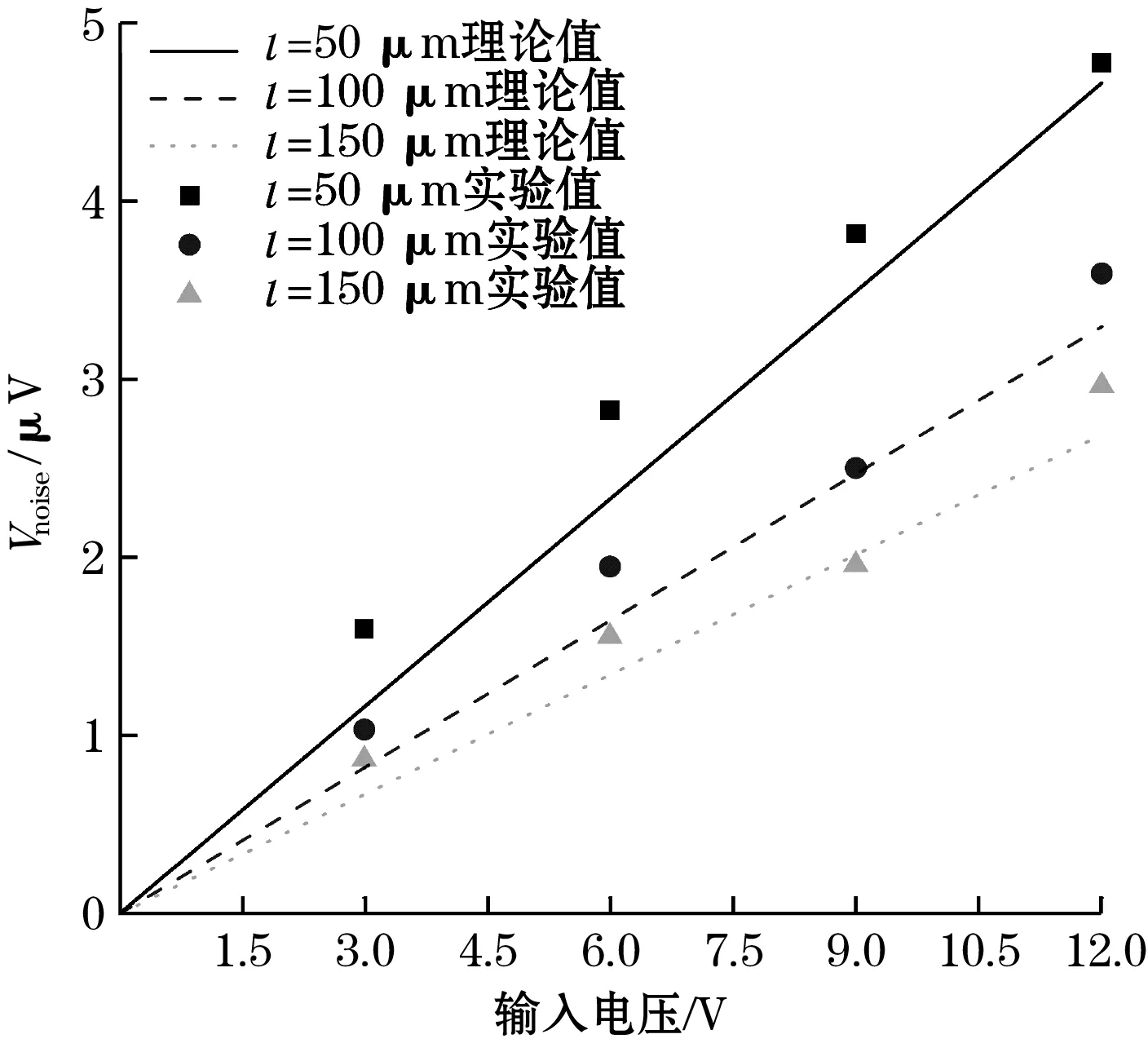
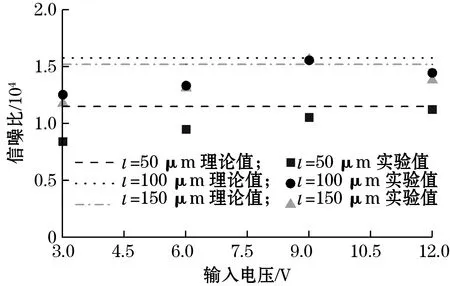
式中:q为掺杂浓度,q=1017cm-3;Vin为输入电压;N为载流子数目;f为噪声频率;a为Hooge因子,是与传感器制作工艺有关的参数,通常10-7 图与f的关系 图6 1 Hz处与n,l的关系 由图5与图6可知各结构传感器主要受闪烁噪声影响。其中低频范围由闪烁噪声主导,只有在高频部分热噪声才会逐渐成为噪声主要成分,且振幅很小。在同一低噪声频率点上,噪声功率谱密度随着n,l的增加而减小。 电路总噪声为测量频带内的噪声功率谱密度之和,通过式(3)和式(5),信噪比SNR即Vout/Vnoise可以表示为 (8) 式中fmax和fmin分别为噪声的上下限截止频率。 图7显示了在6 V输入、1~30 Hz带宽内传感器SNR和n、l关系。由图7可知,信噪比受芯片结构影响,其随n的增大而增大,随l的增大先升后降,最佳电阻长度一般出现在125 μm左右。 图7 SNR与n,l关系 本文采用标准MEMS工艺制作了传感器芯片[11]。制作工艺流程主要包括以下步骤:清洗SOI硅片,离子注入,热氧化形成保护层,光刻刻蚀压敏电阻、接触孔,溅射铝,光刻刻蚀铝、底部硅杯窗口,腐蚀硅杯,去除底部保护层,阳极键合玻璃基底。 经上述工艺制备的传感器芯片如图8所示。本文制得单条型芯片3个,长度分别为50、100、150 μm;多条型芯片长度固定为50 μm,折叠条数分别为2,3,4,6。图9给出了其中1个传感器焊接金丝以及封装完成后的实物图。 图8 MEMS压阻式压力传感器芯片 图9 MEMS压阻式压力传感器 标定测试平台如图10所示,采用PLATINUM真空气压泵和const162台式气压泵分别产生0~100 kPa和100~300 kPa的压力载荷。27 ℃室温下,在压力范围0~300 kPa内,以步进为30 kPa选取压力载荷样本点,输出特性测试如图11所示,图11(a)为单条型,l不同的压敏电阻输出信号与气压关系,图11(b)为l=50 μm,n不同的压敏电阻输出信号与气压关系。由图11可以看出,在0~300 kPa量程范围内,传感器工作良好,线性度较高。 图10 标定测试平台 (a)n=1,l=50、100、150 μm 保持温度不变,在标准大气压下恒压源输入,输出信号Vout中存在来自多方面的噪声,如电源噪声、传感器本身的噪声、测试仪器的噪声、外界环境噪声等。为排除输入端电源噪声,使用电池作为电源;为降低测试仪器的噪声,本实验使用HB-521微弱信号检测装置中的锁相放大器;为屏蔽外界电磁场干扰,使用金属屏蔽盒,各装置之间使用同轴电缆作为导线连接。实验装置如图12所示。 图12 噪声测试实验装置图 将传感器的输出信号Vout接入HB-521锁相放大器中放大,锁相放大器中心频率设置15 Hz,时间常数设为10 ms。使用U型,长度50 μm的压力传感器,在标准大气压下输入3、6、9、12 V电压,测得噪声电压Vnoise的幅频曲线如图13所示。 (a)输入3 V,Vnoise幅频曲线 锁相放大器测得的总噪声包括传感器噪声、放大器噪声和电源噪声,其关系可表示为 (9) 式中:Vsum、Vsensor、Vamp、Vpower分别为总噪声、传感器噪声、放大器噪声和电源噪声。 在电源方面采用了噪声很小的电池作为电源,其噪声可忽略,放大器噪声可通过锁相放大器直接测量小电阻得到。 噪声电压Vnoise与l、n、Vin之间的关系如图14所示。 (a)n=1,l=50、100、150 μm 实验发现闪烁噪声是低频段的主要噪声源,与Vin成正比。当Vin过低,如输入3 V电压时,受放大器噪声影响,Vnoise测量结果误差较大,当Vin较大时,噪声测量结果比较准确。从图14可以看出,Vnoise与Vin整体成正比关系,同时Vnoise随n、l增大而减小。 根据测得的Vnoise、Vout和式(8)可以得到信噪比与电阻结构关系,如图15所示。由图可知SNR不随Vin而改变。Vin较低时由于Vnoise难以精确测量,SNR偏差较大。实验测得的SNR与理论值差距在20%之内,实测值与理论值之间吻合度较好,证明理论分析的可靠性。 (a)n=1,l=50、100、150 μm 本文对基于信噪比的MEMS压力传感器进行设计与分析,首先通过ANSYS有限元模拟仿真各结构传感器的应力分布;其次采用MEMS工艺设计制作了部分传感器芯片,并加工封装;然后利用压力发生装置对传感器进行测试标定;最后输入不同电压,探究MEMS压阻式压力传感器的噪声、信噪比与传感器压敏结构关系。可得到以下结论: (1)通过模拟仿真发现传感器压敏结构对噪声、输出信号和信噪比均存在影响。增加压敏电阻折叠条数通常有助于获得更低的噪声以及更高的输出信号和信噪比,文中基于输出信号和信噪比的最佳电阻长度分别出现在75 μm和125 μm左右。 (2)本文通过实验验证了噪声与输入电压成正比关系,同时Vnoise随n、l增大而减小,SNR不随输入电压变化而改变。SNR主要与传感器结构有关,证明了理论分析的正确性。本文研究结果对于提高传感器信噪比、研制高精度传感器具有一定的参考价值。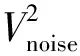
2.2 传感器信噪比分析
3 实验结果与分析
3.1 传感器制备


3.2 气压测量标定

3.3 传感器噪声测量

4 结论

