含冷热电联供的综合能源系统优化调度

陈克文，撖奥洋，周生奇，菅学辉，张智晟

（1.青岛大学电气工程学院，山东青岛 266071；2.国网山东省电力公司青岛供电公司，山东青岛 266002）

当今世界，能源危机、环境污染的压力越来越大，并且工业生产和居民生活对能源的需求也日益增加，如何使能源更加有效地利用，同时使污染物进一步减少，实现能源的清洁利用、可持续发展是当今世界共同关注的焦点[1-4]。综合能源系统（Integrated Energy System,IES）的提出在世界范围内引起了普遍的关注，与传统能源分供的形式相比，它能使能源效益最大化。因此，对于综合能源系统的研究成为现在的重点问题[5-6]。

关于IES 的建模、需求响应及优化调度方法是现在研究的重点。文献[7]考虑碳交易方案和不同的空气污染物控制技术，构建了环境经济调度模型；文献[8]在分析用户能源需求特性和热网的传输特性的基础上，协同优化需求侧、供给侧和传输侧；文献[9]考虑天然气的动态潮流，构建了一种新模型；文献[10]提出了一种考虑电转气设备运行成本对系统风电接纳能力与运行经济性影响的日前调度方法；文献[11]建立了园区综合能源系统的绩效评价指标，从弹性矩阵的角度构建了多能量需求响应模型；文献[12]针对楼宇系统提出一种虚拟储能的调度模式，有效地降低了楼宇的运行成本。

鉴于以上背景，文中构建一种综合能源系统，包含多种能源转换设备便于达到多元化需求，并且考虑系统的运行费用和环境治理费用，使总和最小，通过模拟退火粒子群算法求解该模型，在综合考虑系统多约束条件的情况下，合理调度各个设备的有功功率，以使系统在调度周期内所需费用最少。

1 综合能源系统的优化调度模型

文中研究的综合能源系统由光伏系统（Photo Voltaics,PV）、电制冷机（Electric Refrigerator,ER）、微型燃气轮机（Gas Turbine,GT）、溴化锂制冷机（Lithium Bromide Refrigerator,LBR）、燃气锅炉（Gas Boiler,GB）、燃料 电池（Fuel Cell,FC）和电锅炉（Electric Boiler,EB）等组成。综合能源系统的结构如图1 所示。

图1 综合能源系统结构

1.1 目标函数

1）运行成本

文中构建的综合能源系统的运行成本主要包括三部分，分别为电网购电所需费用、向电网售电所得费用和购气所需费用，即：

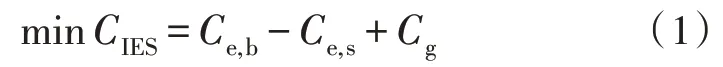
式中，Ce,b为系统产电不足时的购电费用，单位:元；Ce,s为系统售卖电所得费用，单位:元；Cg为购买能源转换设备所需天然气费用，单位:元。

购电费用为:

式中，M为调度周期总时段数；ce,b,t为系统购电单价，单位:元/kW·h；Pgrid,buy为系统从电网购买的电量，单位:kW·h；Δt为单位调度时长，单位:h。

向电网售电所得费用为:

式中，ce,s,t为系统卖电时的单价，单位:元/kW·h；Pgrid,sell为系统售出的电量，单位:kW·h。

购气费用为:

式中，cg为购买天然气的单价，单位:元/m3；VMT、VFC、VGB分别为系统在t时段微型燃气轮机MT、燃料电池FC和燃气锅炉GB所消耗的天然气量，单位:m3。

2）环境成本

在系统的运行过程中，主要考虑处理CO2的治理费用[13]。这部分CO2主要由与电网进行电力交互时燃煤及能源转换设备消耗天然气时产生。因此环境成本Cenv为:

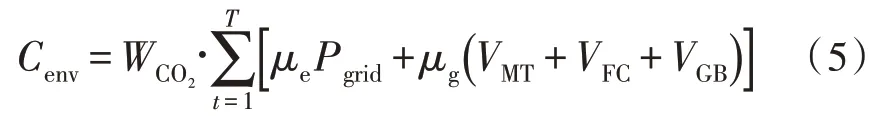
式中，WCO2为系统产生CO2时的惩罚系数；μg、μe分别为单位天然气、单位电功率下CO2的排放量。

系统的总目标函数为:

1.2 各设备的约束条件

1）各设备电、热功率满足功率上下限要求

各设备电、热功率满足功率上下限要求为：

式中，Pi是各设备的电功率；Qi是各设备的热功率；Pimin、Pimax分别是各设备电功率的下限和上限，其电功率上限不得超出额定值，有功功率下限不得小于0；Qimax、Qimin分别是电锅炉等产热设备热功率的上限和下限，其设定同上。

2）电功率平衡约束

在系统中，电功率应在各个时刻保持各设备有功功率及负载消耗的平衡,如下式:

式中，PPV、Pele、PFC、Peb、PMT分别为光伏机组、电制冷机、燃料电池、电锅炉、燃气轮机的电功率；Puser表示第t时段满足系统约束时优化调整后的电负荷需求；Pgrid为正表示从电网购电，为负表示向电网售电。

3）供气平衡约束

供气平衡约束如下:

式中，Vg为从天然气网中获取的天然气量；Vuser为用户侧用气负荷所需量。

4）冷能平衡约束

冷能平衡约束如下:

式中，Quser为系统中用户的冷负荷；Qco为溴化锂制冷机的制冷功率；Qele为电制冷机的制冷功率。

5）热能平衡约束

热能平衡约束如下:

式中，Huser为用户的热负荷；HGB为燃气锅炉的产热功率；HEB为电锅炉的产热功率。

2 模型的求解方法

2.1 模拟退火粒子群算法

由于粒子群优化算法（Particle Swarm Optimization,PSO）容易困入局部极值，因此文中将模拟退火[14]思想（Simulated Annealing,SA）和Metropolis 准则引入粒子群优化算法中。当受到扰动而产生的新粒子为x′，粒子群的当前最优粒子为pbest，两者之间的适应度差值可以表示为:

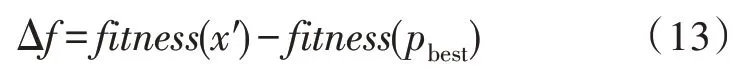
若Δf＜0，即新粒子的适应度值比当前最优粒子的适应度值小，那么接收新粒子为最优粒子；反之，以的概率接收这个粒子。这就是Metropolis 准则，其中T为模拟退火过程中的当前温度。文中适应度值代表综合能源系统中的总成本。

2.2 算法流程

该算法优化系统中各能源转换设备的功率，从而使算法中的适应度值即系统的总成本最小。

算法的具体步骤如下：

1）设定粒子群的规模，生成各个粒子一定范围内的初始状态。

2）根据式（14）和式（15）更新粒子状态，搜索个体和全局最优粒子。

式中，c1和c2为学习因子，一般取两者相等；ksi为惯性因子，可根据需要设定；r1和r2为0 到1 中的无规则数；xi,j(t)和vi,j(t)分别为粒子的位置和速度；pi,j为迭代至目前所找到的个体最优值；pg,j为全局最优值。

3）对当前粒子群进行扰动，计算扰动后的个体和全局最优粒子。

4）如果重新搜索到的扰动后的全局最优粒子优于扰动前的最优粒子，则接收该粒子并将其作为新的全局最优解，反之不接收。如果扰动后的解满足准则，则接收此解作为新的个体最优粒子，反之不接收。

5）根据Tk+1=λ×Tk执行退温操作，使温度T不断下降，其中λ为退温常数，初始温度T0=fitness(pg)/log(5)。如果搜索到的解已经满足条件，则不再搜索，输出最终结果；反之，回到第2）步，继续搜索最优解。

3 算例分析

3.1 综合能源系统的仿真算例

为了验证模型及算法的有效性，文中以某建筑楼宇综合能源系统[15-16]为实际算例，该办公楼建筑面积为1.5万m2。该建筑吸收来自光伏、电网、燃料电池及燃气轮机的电能；热负荷由燃气锅炉及电锅炉提供。

取某一夏季典型日为一个完整的调度周期，每一个小时为一个时段，一个调度周期内共包含24 个时段。建筑的光伏出力及冷、热、电负荷如图2 所示。分析该算例时采用分时电价，峰时段（10:00-15:00、18:00-21:00）、谷时段（23:00-次日6：00）及平时段（其他时间）的购电价分别为1.00元/kW·h、0.38 元/kW·h、0.70 元/kW·h；售电价分别为0.70 元/kW·h、0.25元/kW·h、0.40 元/kW·h。

图2 内部负荷及光伏出力

3.2 算法结果的对比及分析

用两种算法对综合能源系统模型进行求解，图3为两种算法适应度的变化对比，图4 为各个设备的出力数据。

图3 两种算法的对比

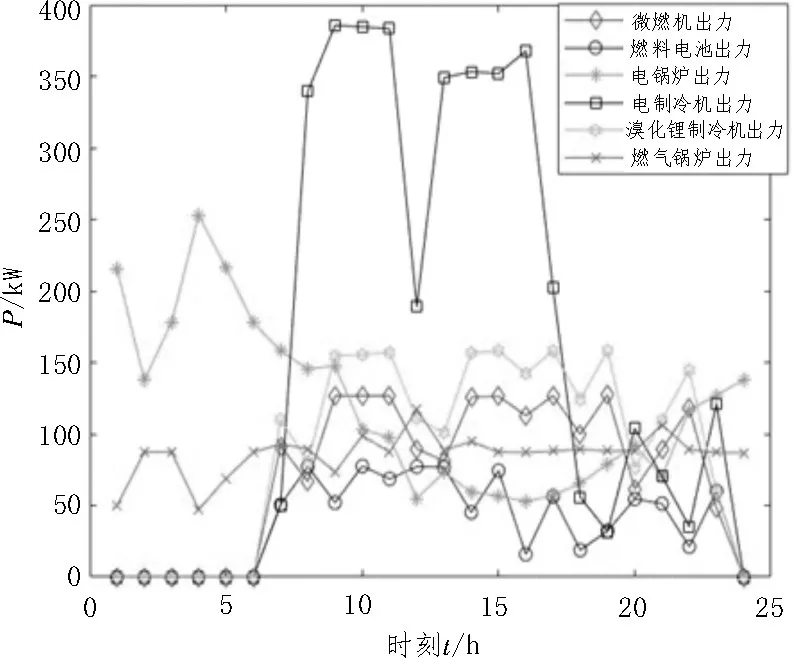
图4 各设备的出力

从图3 可以看出，在两种算法迭代次数相同（均为1 000 次）的情况下，SAPSO 算法的整体效果要优于PSO 算法。尽管基本粒子群算法在前期搜索速度快，但是容易陷入局部极值，从而较早的收敛；而模拟退火粒子群算法能够跳出局部极值，全局搜索能力更强，收敛的效果优于基本粒子群算法。

如图4 所示，在谷时段，由于此时电价较低，因此向电网买电用于满足整体电负荷需求，所以燃气轮机的功率逐渐减小，电锅炉的功率较大，电制冷机功率逐渐下降；在峰时段，电负荷、冷负荷需求量整体处于上升趋势，并趋近于峰值，所以燃气轮机发电量逐渐增大，且燃气锅炉工作在较高功率状态；由于燃气轮机处在功率较高的工作状态时，产生的余热较多，因此溴化锂吸收式制冷机功率较高，但仍不能满足此时的冷负荷需求，因此电制冷机的功率仍然较高，溴化锂吸收式制冷机与电制冷机共同工作以满足冷负荷需求。

两种算法的系统成本如表1 所示。与传统粒子群算法相比，利用模拟退火粒子群算法得到的系统总成本更低，减少了约5.9%，充分说明了该算法的有效性。

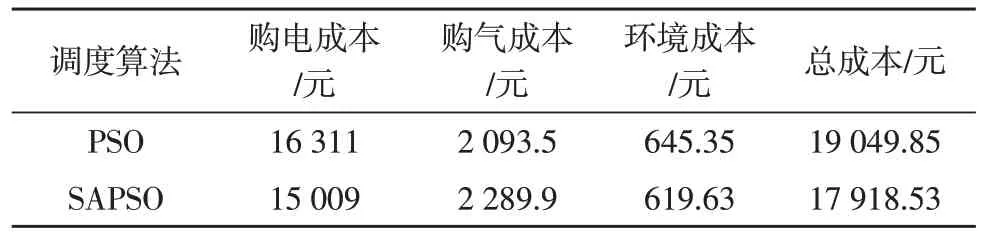
表1 两种算法的成本对比

4 结论

文中针对综合能源系统能源需求增长迅速但能源供给结构不合理的问题，构建包含运行费用和环境治理费用的目标函数，利用模拟退火粒子群算法对模型进行求解。通过仿真分析可知，与传统粒子群算法相比，模拟退火粒子群算法能够有效减少综合能源系统在调度周期内的总成本，该模型能够有效平衡系统的经济及环境效益，满足生产时的多目标需求，为综合能源系统的规划运行奠定基础。但是模拟退火粒子群算法也有着收敛性慢的问题，需要更多的迭代次数，找到最优解所需的时间也更长，在今后的研究中可以对此进行优化。