采用状态反馈的无人车路径跟踪横向控制

寇发荣，杨慧杰，张新乾，郑文博，王思俊

(西安科技大学 机械工程学院,西安 710054)

智能化和网联化是未来汽车发展的趋势[1]。无人驾驶车辆将环境感知、自主决策与规划、动力学控制[2]等关键技术整合,从而提高道路安全性与利用率、车辆智能化水平[3]。路径跟踪算法是智能车辆动力学控制的核心问题,车辆需要按照预设路径行驶,同时保证行驶精度和稳定性。

模型预测控制作为一种车辆路径跟踪优化控制算法,通过对线性模型的输入和状态变量添加约束,可将结果转化为带约束的最优控制问题[4-5]。线性时变模型预测控制在车辆路径跟踪实时性控制中有明显的优势[6]。采用动力学模型的路径跟踪控制器考虑轮胎与地面的附着极限,车辆可以在复杂路面下以高速稳定行驶。国内外学者在车辆路径跟踪模型预测控制领域做了大量研究: Falcone等[7]研究了用于车辆动力学的模型预测控制器设计和实现问题,并通过实车试验验证了高速车辆的稳定性。斯坦福大学学者使用模型预测控制器和反馈控制器设计框架,协调解决了车辆紧急避撞及其稳定性问题[8]。国内学者采用模型预测控制方法对车辆底盘集成控制和稳定性开展研究[9-10]。针对路径跟踪控制器跟踪精度问题,赵治国等[11]采用粒子群优化算法实现了预瞄距离自适应控制;白国星等[12]分析了车辆稳态转角、车速和预测时域的变化规律,通过调节参数实现路径跟踪控制器的改进优化。上述文献中采用的路径跟踪模型预测控制算法在弯道内路径跟踪精度难以保障,行驶时会出现转向系统反应超前或滞后[13],从而影响控制器跟踪效果。状态反馈控制方法能够实现闭环控制,达到系统期望的性能指标。斯坦福大学Snider[14]将状态反馈控制器运用于路径跟踪控制。Kapania等[15]使用稳态质心侧偏角跟踪参考轨迹方向,改善了路径跟踪性能。魏建伟等[16]基于LQR最优控制提出了主动转向和直接横摆力矩控制的联合控制策略,提高了车辆的侧向稳定性。线性二次调节器LQR通过状态反馈实现闭环控制,其性能指标是关于状态变量和控制变量的二次型函数,可以实现系统控制过程中的动态误差和能量消耗最低[17]。

本文提出了一种基于状态反馈的路径跟踪模型预测控制方法。以车辆动力学模型建立路径跟踪模型预测控制器,选择合适的控制器时域参数值,在前轮主动转向的基础上以车辆当前位置的横摆角偏差设计状态反馈调节器,使用LQR算法对转向角进行校正,最后利用MATLAB/Simulink和Carsim软件进行联合仿真分析验证算法的有效性。

1 车辆状态反馈控制系统框架

1.1 车辆动力学模型

路面附着、轮胎等非线性因素对无人驾驶车辆转向特性有显著影响,给控制器设计带来一定挑战。为准确描述这些影响因素,忽略车辆垂向运动和轴荷转移,对车辆模型进行适当简化使其具有横向、纵向和横摆这3个自由度,简化后的车辆动力学模型如图1所示。图中：XOY为固定于地面的惯性坐标系;xoy为固定于车身的车辆坐标系;o为车辆质心位置;x轴沿车辆纵轴方向;y轴与车辆纵轴垂直。

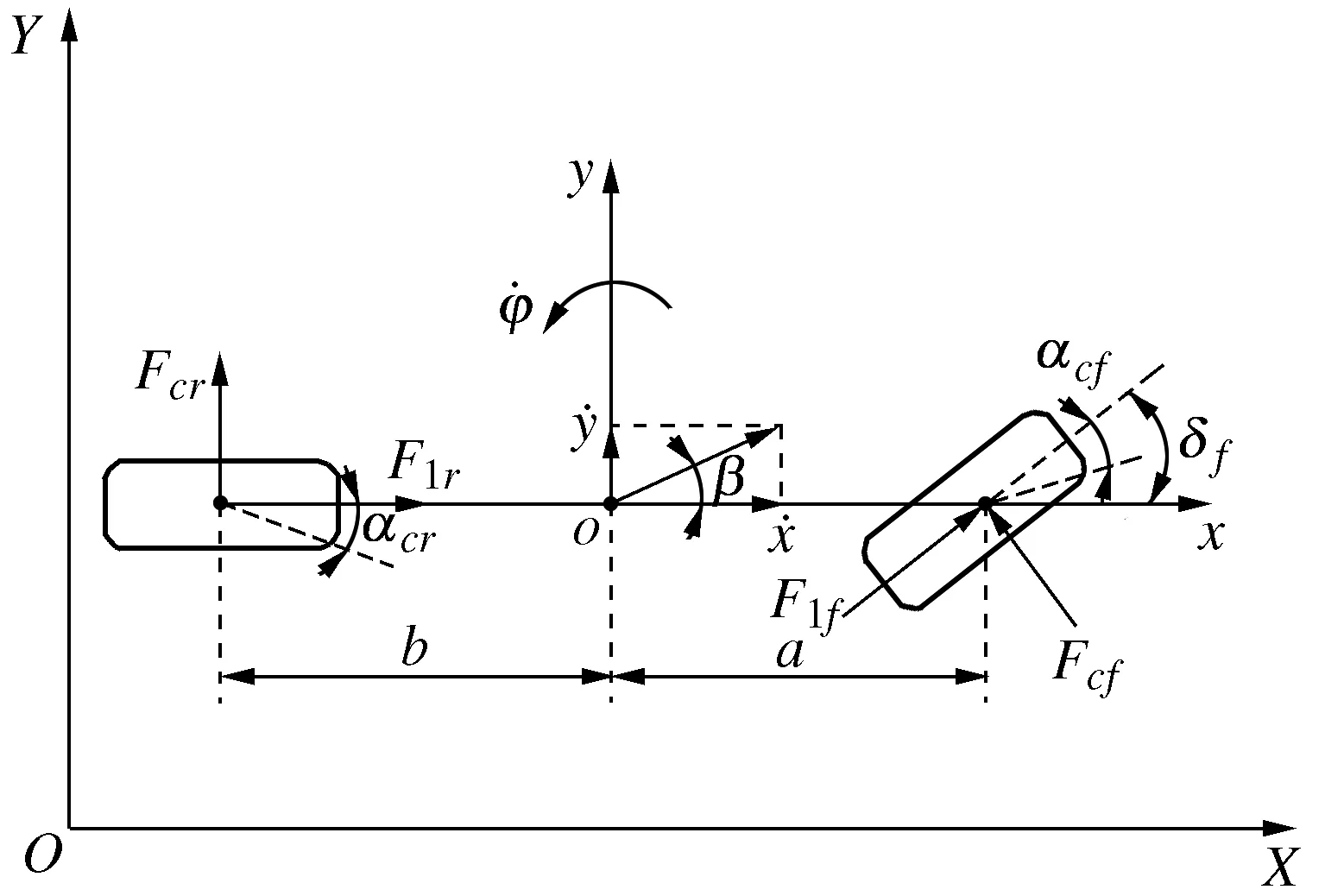
图1 3自由度车辆模型

根据牛顿第二定律,得到沿x轴、y轴和z轴的受力平衡方程，即

(1)

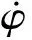
考虑到前轮转角较小,轮胎所受纵向力和侧向力呈线性变化,将其表示为轮胎侧偏角和滑移率的线性关系，即

(2)

式中：Ccf、Ccr为前后轮胎侧偏刚度;Clf、Clr为轮胎纵向刚度;slf、slr为轮胎滑移率；αcf、αcr为前后轮胎侧偏角。

最终得到基于线性轮胎模型和小角度假设下的车辆非线性动力学模型:

(3)

1.2 车辆状态反馈控制器

智能车辆路径跟踪控制框图如图2所示。

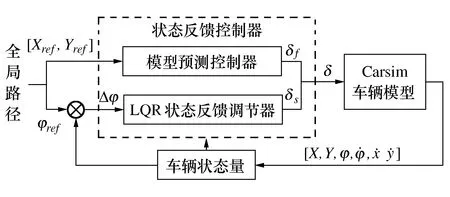
图2 路径跟踪控制器框图

路径跟踪状态反馈控制器包括模型预测控制器(MPC)和LQR状态反馈调节器两部分。模型预测控制器根据道路信息和车辆约束条件计算出预测时域内前轮转角,状态反馈调节器根据道路参考横摆角φref和车辆实际横摆角φ计算横摆角偏差Δφ,并通过LQR算法对车辆前轮转角进行校正,最终将修正后的转角δ输出到Carsim中实现对车辆的控制。

2 模型预测横向控制器设计

基于状态空间的模型预测控制算法具有预测模型、滚动优化和反馈校正3个特征,该算法汲取反馈控制思想,预测时域的滚动优化使系统在受到内部或外界的扰动时及时补偿和校正,具有很强的鲁棒性[4]。

(4)

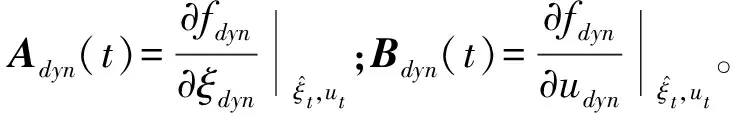
计算机对连续系统作实时控制,需要使用一阶差商的方法将式(4)线性时变连续系统进行近似离散化,得到离散的状态空间表达式为

(5)

其中:

Ak,t=I+TAdyn(t);Bk,t=TBdyn(t)。

模型预测控制器根据系统预测模型下一时刻输入量和当前时刻状态量,确定未来预测时域内的输出,由式(5)动态方程将系统未来一段时域的输出表示为

Y(t)=ψtξ(t)+ΘtΔU(t)

(6)

其中：

将预测时域内输出量和时域内的控制增量作为优化目标,使系统稳定的跟随期望轨迹,得到最终的目标函数为

(7)

式中:Q、R、ρ为权重系数矩阵;ε为松弛因子,防止计算过程中出现无解情况。

考虑系统中控制量和控制增量极限约束,同时由车辆横向速度和横摆角速度定义车辆滑移稳定包络线约束[18]。车辆在稳态条件下的横摆角速度为

(8)

临界条件下假设轮胎纵向力为0,得到横摆角速度极值为

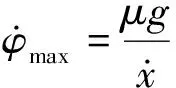
(9)

车辆稳定性条件的另一个约束是后轴轮胎的侧向力饱和,后轮侧滑造成整车失控危害较大,需要对轮胎侧偏角进行限制。

由图1可得到后轮侧向力产生的侧偏角,后轮侧偏角与质心运动参数的关系为

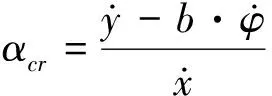
(10)

车辆最大侧向力产生的后轮最大侧偏角为

(11)

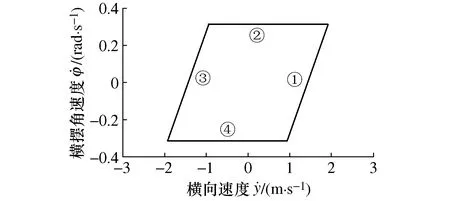
图3 车辆滑移稳定性包络线约束

式(9)和式(10)也可以表示为矩阵形式

|H(t)·ξ(t)|≤G+s

(12)

综合上述条件,基于模型预测控制器的无人车前轮转角最优控制问题可以转化为最优二次型:

minJ(ξ(t),u(t-1),ΔU(t))

(13)

3 LQR状态反馈调节器设计

3.1 车辆跟踪误差模型

车辆在弯道行驶时的跟踪误差模型[19]如图4所示,模型参考点位于质心o处,选取路径点P定义车辆当前位置行驶偏差,其中横摆角偏差Δφ是期望路径点切线与车辆x轴夹角,ye为车辆横向位置偏差,车辆x轴与行驶车速v之间的夹角为质心侧偏角β,路径点P处的曲率半径为Rref。

图4 车辆跟踪误差模型

由图4几何关系可得,车辆当前时刻的横向偏差变化率为

(14)

在小角度假设下,由sin(β+Δφ)≈β+Δφ,将三角函数线性化

(15)

车辆沿期望路径行驶时,质心处的横摆角偏差变化率为

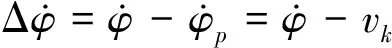
(16)

由于路径跟踪模型预测控制器弯道内过早转向,导致车辆行驶轨迹偏向于弯道内侧。本文参考斯坦福大学stanley路径跟踪控制算法思想[20],以车辆质心位置为控制点,通过转向角补偿校正实现车辆横摆角偏差反馈控制,同时降低当前位置的横向偏差,使车辆行驶方向更接近参考轨迹切线方向。

由此得到车辆当前位置所满足的运动学跟踪误差模型表达式为

(17)

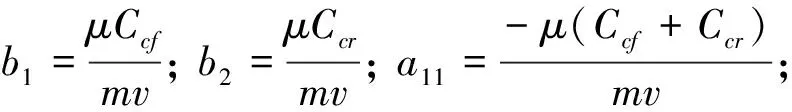
式中:μ为道路附着系数;k为曲率;δf为模型预测控制器计算得到的前轮转角;δs为转角校正量。

3.2 基于误差模型的状态反馈调节器设计

状态反馈调节器可以保证闭环系统稳定,同时改善控制器路径跟踪性能。本节结合车辆跟踪误差模型得到横摆角偏差,利用LQR控制方法构建状态反馈调节器。

由式(17)状态空间方程构建二次型性能指标:

式(18)指标中第一项反映了系统对调节过程的平稳性和快速性要求,第二项反映了对能量消耗的要求。系统受到扰动偏离参考轨迹时,需要产生附加方向盘转角,使跟踪横摆角偏差Δφ和能量消耗综合最优。

应用拉格朗日乘子法构造无约束优化问题,建立增广泛函，即

定义哈密尔顿函数为

H[x,u,λ,t]=θ=F[x(t),u(t),t]+λTf(x,u,t)(20)

使用黎卡提微分方程解出P(t)矩阵

P(t)B(t)R-1(t)BT(t)P(t)-Q(t)

(21)

将P(t)代入式(22)最终可得最优控制量u*(t)为

u*(t)=-R(t)BTP(t)x*(t)=-K(t)x*(t)

(22)

式中K(t)为反馈增益矩阵。

4 路径跟踪控制器仿真分析

4.1 仿真道路及控制器参数设置

为验证基于状态反馈的模型预测控制器跟踪效果,本节设计了路径跟踪仿真对比试验。双移线道路包括连续转弯和回正操作,能够全面测试车辆弯道内的轨迹跟踪性能,因此采用双移线测试路段,路面附着良好,无路面超高。图5为双移线轨迹及参考横摆角曲线,路径纵向位移设置为200 m,曲率随路径变化,最小曲率半径30 m,位于X=60 m处。

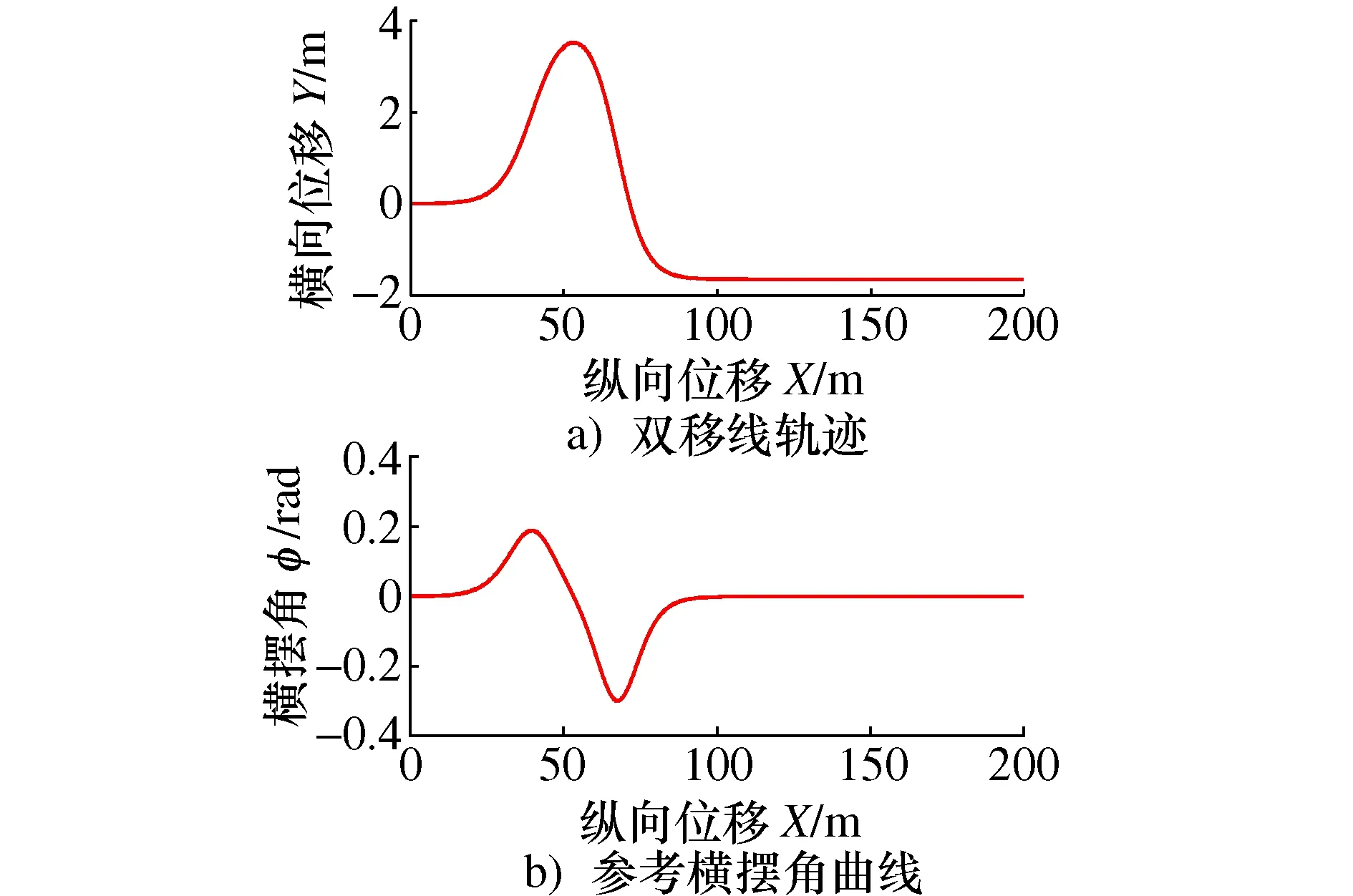
图5 双移线工况

由于模型预测控制器跟踪误差与预测时域步长、车速和道路曲率的关系难以用函数关系式表示,因此以车辆在双移线轨迹的行驶数据为误差参考依据: 给出离散时间步长一定时,不同预测时域下车辆路径跟踪横向偏差的均方根值,使车辆能够根据不同行驶工况选择合适的控制器时域步长值。

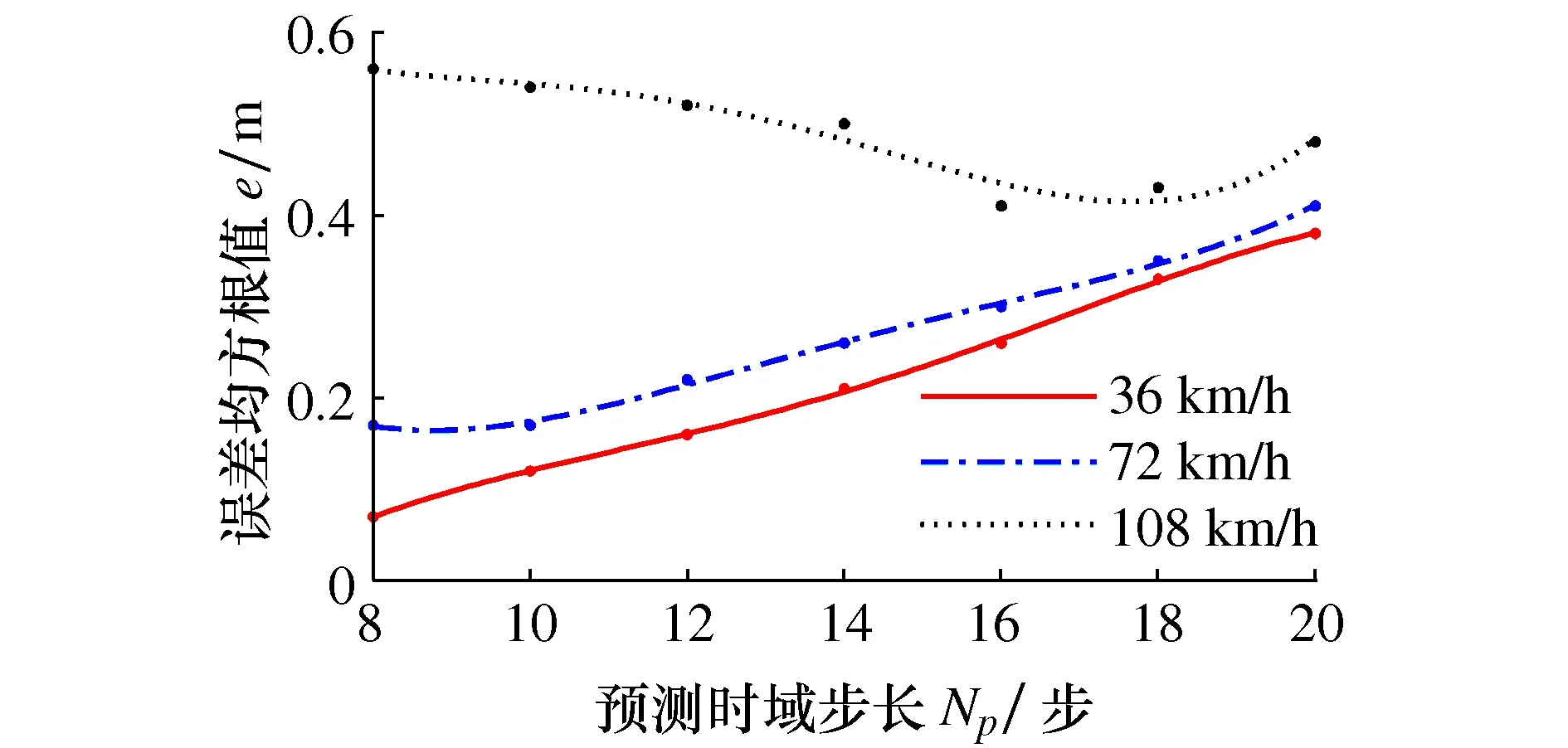
图6 不同车速和预测时域的跟踪误差

图6中曲线为3个速度下不同预测步长的跟踪误差均方根值。由图6可知,车辆以36 km/h和72 km/h车速在弯道行驶时,预测时域步长与跟踪误差成正比关系,预测时域越长,跟踪误差越大;在108 km/h车速下,随着预测时域步长增加,跟踪误差先减小后逐步增大。同时预测时域步长不应过小,小步长易使车辆绕参考轨迹摆动,中高速情况下容易失去稳定性。由此可以确定不同速度下合适的预测时域步长,结果如表1所示,其它速度区间的最佳时域步长可以通过线性回归预测得到。

表1 不同速度下确定的预测步长

本文使用Carsim搭建整车模型,仿真所用车辆模型为前轮驱动C级轿车,模型及仿真过程中的参数设置如表2所示。

表2 车辆参数及权重矩阵设置

4.2 路径跟踪控制器对比分析

将基于状态反馈的路径跟踪模型预测控制器与传统模型预测控制器的车辆行驶轨迹、横摆角及偏差曲线进行对比分析。不同车速下改进控制器性能表现不同,本文分别在36 km/h、72 km/h和108 km/h速度下进行仿真试验,采用车辆参考轨迹与实际行驶轨迹误差平均值和最大值指标作为衡量轨迹跟踪精度好坏的依据,并结合仿真结果分析车辆在不同控制器下的路径跟踪效果。

图7为36 km/h速度下得到的仿真结果,图7a)为车辆行驶轨迹,图7b)和图7c)为车辆相对参考轨迹的横向偏差和横摆角偏差,图7d)为前轮转角对比图,算法改进前后车辆轨迹和前轮转角的结果对比通过箭头标注。

图7 36 km/h车速仿真结果

从图7a)曲线可以看出,采用传统模型预测控制的车辆在40～50 m区间入弯较晚,在60～70 m区间因提早转向而驶离车道,车辆进入下一弯道时导致偏差累积,而使用本文方法的车辆在驶入和驶离弯道时更加接近参考轨迹。由图7b)和图7c)可以看出,车辆行驶最大偏差出现在弯道内,传统模型预测控制器的最大横向偏差和横摆角偏差都大于状态反馈控制器。由图7d)车辆前轮转角对比分析可知,车辆在40～50 m和60～70 m弯道内校正后的方向盘转角幅值略大于传统模型预测控制器,意味着车辆入弯时刻更早,而出弯时刻稍晚,同时可以看出进入下一弯道后转向更快速,有利于车辆提升弯道跟踪的准确性。由计算可知,双移线工况下,汽车以36 km/h定速行驶,使用本文方法的控制器横向误差平均值为0.138 m,误差最大值为0.353 m,位于横向位置74 m处;而传统模型预测控制器横向误差平均值为0.165 m,误差最大值为0.518 m,位于横向位置76 m处。

图8为车辆以72 km/h行驶时得到的仿真结果。

图8 72 km/h车速仿真结果

从图8a)中曲线可以看出,在40～50 m和60～70 m区间车辆变换弯道时,两种控制方法下车辆驶离弯道的位置基本相同,使用本文方法的车辆横向位置误差和横摆角偏差更小。从图8b)和图8c)可知,基于状态反馈的路径跟踪控制器横向偏差和横摆角偏差均得到明显改善。由图8d)可知,在位置50～60 m区间,使用本文方法的车辆前轮转角在达到最大值后没有立刻回正,而持续了一小段时间,由图8a)可知此时弯道内使用状态反馈控制器的车辆更加接近参考轨迹。由计算得状态反馈控制器横向误差平均值为0.148 m,误差最大值为0.454 m;传统模型预测控制器横向误差平均值为0.225 m,误差最大值为0.681 m。

图9为车辆以108 km/h行驶时的仿真结果。

图9 108 km/h车速仿真结果

由于车辆高速行驶时轮胎接近附着极限,两种控制方法得到的路径跟踪误差均较大,在动力学约束条件下本文方法对高速弯道轨迹改善程度较小。

车辆行驶偏差数据对比如表3和表4所示,由表可以看出,72 km/h速度下基于状态反馈的跟踪控制器行驶精度改善程度最大,车辆横向偏差平均值和幅值降低33%以上,横摆角偏差的幅值降低达61%;36 km/h速度下也有很好的跟踪效果,车辆在中低速过弯时车辆偏差的最大值和平均值均小于传统模型预测控制器;而以108 km/h高速行驶时横摆角偏差有所改善,横向偏差最大值有所增加。但由于弯道内行驶车速一般较低,故基于状态反馈的模型预测控制器能够适用于弯道行驶。

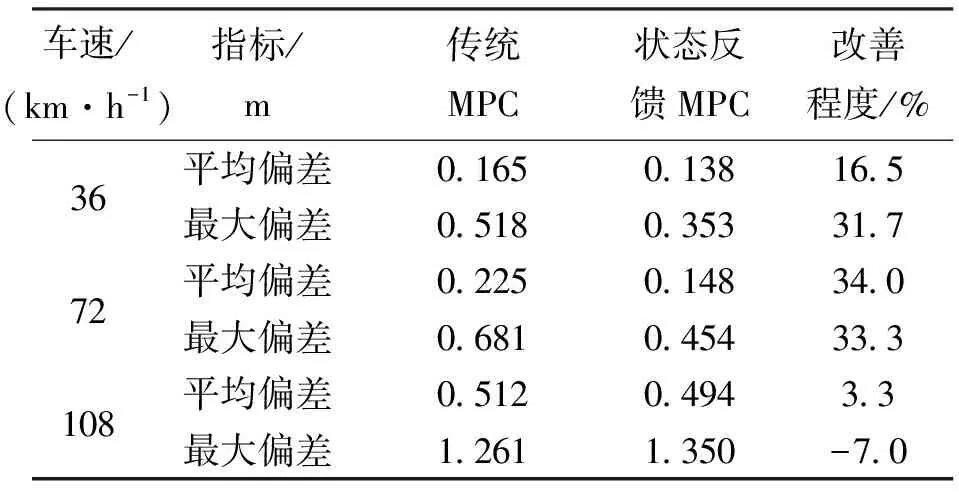
表3 双移线工况横向偏差对比

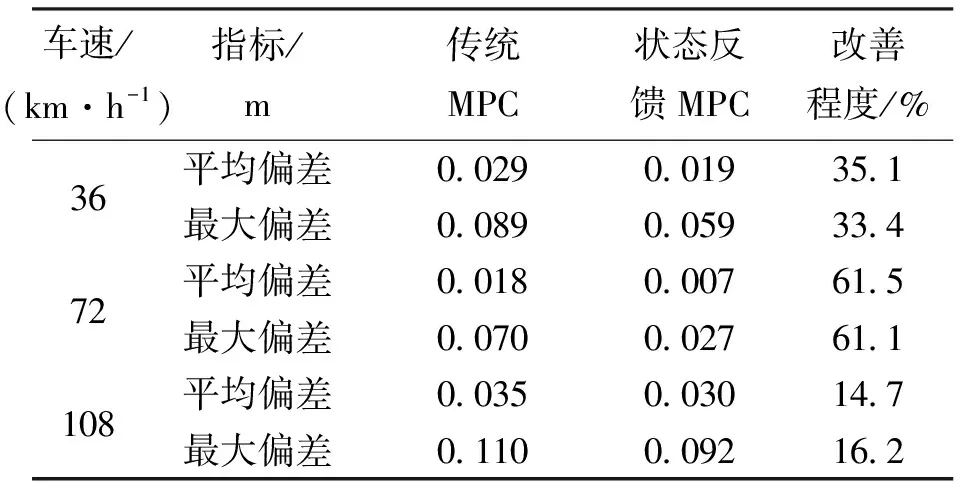
表4 双移线工况横摆角偏差对比

5 结论

本文为解决车辆驶入和驶离弯道时行驶精度低的问题,提出了基于状态反馈的路径跟踪横向控制策略。在路径跟踪模型预测控制器基础上,对于复杂行驶路况,在满足控制量约束和输出量约束的横向控制器基础上,加入针对轮胎的滑移稳定性约束,提高车辆行驶安全性,根据工况调整合适的控制器时域参数使误差均方根值最小。在传统模型预测控制器基础上,建立了基于LQR的状态反馈调节器。以路面附着良好的双移线道路为基本仿真工况,通过MATLAB/Simulink和Carsim对所设计的控制器进行仿真验证,结果表明:相比于传统模型预测控制器,基于横摆角偏差反馈的改进状态反馈控制器在36 km/h车速下横向偏差降低了16%以上,横摆角偏差降低了33%以上;72 km/h车速下横向偏差降低了33%以上,横摆角偏差降低了了61%以上;108 km/h车速下偏差略有改善,验证了改进控制器能够提升车辆弯道内中低速行驶时的跟踪精度,使车辆驶离弯道时不会过早的转向而偏离车道。