结构形式对泵站前池流态影响的数值模拟研究

许经宇，韩冬梅

（吉林省水利水电勘测设计研究院，吉林长春 130021）

泵站前池是引水管（渠）和进水池的连接建筑物，其大小和形态不仅对工程的稳定运行和经济性产生一定的影响，还会影响其水流流态。近年来，在一些工程中，对前池结构的设计容易忽视，从而导致工程投资浪费，更严重的是引起进水池流态紊乱，泵站机组振动，水泵效率不足，还会造成局部淤积等问题。因此，在泵站前池进水流态分析研究的基础上，优化前池的形状和尺寸，是泵站工程主要问题之一。下文通过对吉林省白城市老白沙滩泵站改造工程的工程实例进行数值模拟研究，为其他工程提供参考。

1 工程概况

吉林省西部地区雨洪资源综合利用河湖连通供水工程白城市老白沙滩泵站改造工程位于白城市镇赉县丹岱乡。老白沙滩泵站水泵为立式混流泵，叶轮直径965 mm，出水口径1 400 mm，额定转速496 r/min，在设计总扬程12.00 m时，流量为3.7 m3/s；水泵最大总杨程为12.50 m，最小总扬程为5.70 m；配用电机型号YL630-12，单台异步电机功率630 kW，额定电压Ue=10 kV，最大轴功率约538 kW。机组台数前期安装3台，后期增加至5台。前池形状设计方案为矩形侧向泵站前池和优化后的收缩侧向泵站前池，每种前池考虑5台机组运行和3台机组运行两种工作状况。前池水位为设计水位128.5 m，水深5.00 m，流量为18.5 m3/s（5台机组）和11.1 m3/s（3台机组）。

此次前池流态研究利用商用CFD软件CFX，基于定常不可压缩流体的连续性方程、雷诺平均纳维-斯托克斯方程（RANS）和标准k-ε湍流模型完成数值模拟计算。

2 数值模拟理论

2.1 数学模型与控制方程

此次研究数值模拟采用基于Boussinesq涡团粘性模型假定的k-ε二方程模型。

湍动能k的输运方程：

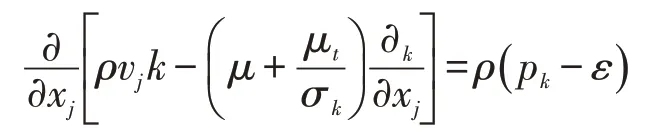
耗散率ε的输运方程：

式中：xj为坐标；vj为y方向雷诺时均速度；μ为动力粘性系数；ρ为流体密度；μt为涡团粘性系数，；pk是湍动能生成项vi为x方向雷诺时均速度；σk，Cμ，Cε1，Cε2，σε为经验系数，Cμ=0.09，Cε1=1.44，Cε2=1.92，σk=1.0，σε=1.3。

式中：xi(i=1，2，3)代表坐标系坐标轴；p*是包括湍动能k的静压力，即p*=ρk；ueff为有效黏性系数，等于分子黏性系数u与Boussinesq涡团黏性系数ut之和，即ueff=μ+μt。

2.2 控制方程的离散

控制方程的离散是将偏微分方程离散为网格节点上的代数方程，有限元法、有限差分法和有限体积法（控制体积法）等为其主要常用方法。有限体积法（控制体积法）是将控制微分方程对所有的控制体积积分，得到一组以网格节点的因变量为未知数的离散方程，因变量在控制体积中满足守恒原理，物理意义明确，已成为最常用的离散方法。老白沙滩泵站的三维湍流数值模拟研究采用有限体积法。

2.3 数值计算方法

数值模拟试验采用了分离式解法中的原始变量法，具体为Van Doormal和Raithby提出的SIMPLEC（Semi-Implicit Method for Pressure-Linked EquationConsistent）压力修正算法。

2.4 边界条件

1）进口边界条件

数值模拟泵站前池流场时，进水边界设在白沙滩防洪闸海漫段上。并假设流速与进口断面垂直，海漫段水流流态为湍流。

2）出口边界条件

数值模拟泵站前池流场时，出水边界设在进水池向后延伸段上。假设出口断面水流为已充分发展的湍流，流速垂直出口断面。采用第二类边界条件，∂φi/∂n=0，其中φi代表不同的因变量，n为出口断面外法线。

3）固壁条件

设在固体壁面上满足无滑移条件，即速度v→=0；压力P取为第二类边界条件，即∂P/∂n=0。因靠近固壁面处的速度梯度较大，充分发展的湍流模型在此区域适用。因此，在对实际工程的数值模拟计算中，通常采用壁面函数法（Wall Function Law）。

4）自由面条件

假设自由水面波动不大，数值模拟计算中采用静水压力假定，可以作为对称边界条件。

5）动静交界面处理

由于水泵类的转轮机械，在转轮区域和井筒等相对静止的空间之间会出现一种动静衔接的关系，同时由于水流的自身性质还会有一定的耦合作用。对于上述问题，通常有3种解决方法：多重参考坐标系模型、混合平面模型和滑移网格模型，此研究中的泵装置整体计算采用了多重参考系模型。理论路线为用某一时刻的瞬态流场代替连续的动态流场，用定常方法分析解决非定常问题。在惯性坐标系中的相对静止构件可以采用定常计算，相对运动或转动的构件则采用离心力和科氏力进行定常计算；在动静变化的空间衔接处，则采用惯性坐标系中的绝对速度，保证其连续性。

3 泵站前池流态分析

3.1 模型建构与网格剖分

利用三维实体造型软件Croe和前处理软件Gambit建构三维物理模型及网格剖分，分块混合网格，网格数在140万（5台机组）和110万（5台机组）左右，如图1所示，经检查网格质量良好。

图1 前池三维造型

3.2 流速分布情况

结合白沙滩泵站前池的结构特点，对典型断面进行了分析计算。其中垂直于X方向3个断面；垂直于Z方向5个断面（5台机组）和3个断面（3台机组）；水平特征断面3个。另外，还采用了迹线分布模拟分析了水流运动轨迹。以设计水面高度特征断面为例，各方案水流流速分布云图如图2所示。

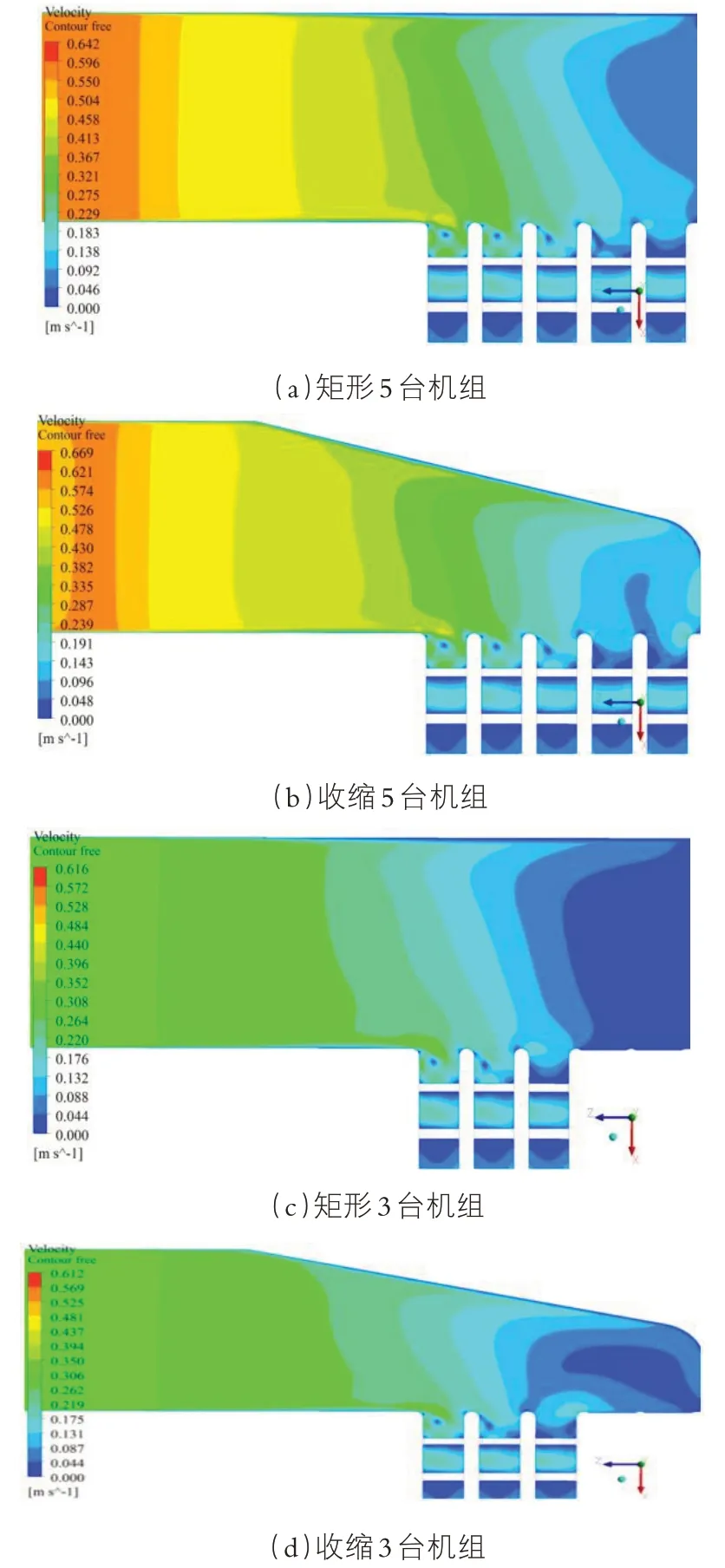
图2 水面流速分布云图

3.3 水力损失

提取前池进口断面和进水池进口断面计算结果数据，采用微元面积加权平均法计算两断面的总能量，进而计算两断面总能量的损失，即前池的水力损失△h，进一步可算出阻力系数s，计算公式：

式中：Ai为面积（若干微元）；参数下标数字1和2为流道上游和下游。各计算方案的水力损失值及损失系数，见表1。

表1 水利损失结果表

3.4 优化目标函数值

在设计流量运行时，水泵系统与流场的相互作用主要特点表现为转轮所在平面与进水角度垂直和管道断面流速均匀。因此，可以采用流速分布均匀度函数Vu和流速加权平均角度θˉ，其定义：

通常用于反映进水流道出口处或水泵进口处的流态状，此处借用该参数在一定程度上定量描述进水池进口处的流态，此数据只具有参考意义。从计算结果中提取进水池进口断面数据，经计算后得到各目标函数值，见表2。

表2 优化目标函数结果表%

3.5 流量分配情况

设计良好的前池应该能为每个水泵机组均匀分配流量，侧向进水泵站更应重视流量分配问题。在CFX Post可直接计算出各进水池流量，见表3。

表3 流量分配情况表m3/s

3.6 流态分析结果

从图2可见：矩形前池与收缩前池中主流区的流态无太大区别，各进水池进口附近流态相似。5台机组运行时，由于流速较大，台阶后有小范围竖向回漩，但对进水池进水影响不大。粒子运动轨迹模拟分析结果与流态分布图展示的流态基本吻合：前池中水流从渠道到进水池，由于流速低，流态较平顺。同样因为前池流速低，矩形前池与收缩前池的水力损失、阻力系数和进水池进口处流速分布均匀度相差极小。3台机组运行时的流速分布均匀度略好于5台机组运行；但分配流量方面，无论是5台机组运行还是3台机组运行，矩形前池的流量差异都小于收缩前池。

4 结语

通过以上对老白沙滩泵站侧向进水前池流态分析，可知矩形前池与收缩前池的水力性能差异极小，分配流量性能矩形前池略优。从简化设计，方便施工角度考虑，建议采用原设计矩形前池作为实施方案。