基于关联网络的机器人移动货架系统货位分配方法

胡祥培 丁天蓉 张源凯 庄燕玲

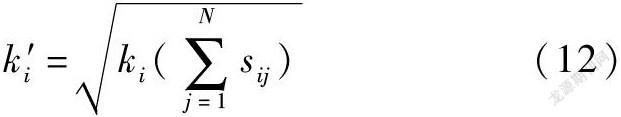
摘 要：作为一种新型智能订单拣选系统，机器人移动货架系统为解决大型网上超市面临的一单多品订单拣选难题提供了前所未有的机遇，而货位分配是关系该系统运行效率最为核心的关键环节之一。针对该系统一品多位货位分配问题带来的商品关联关系复杂、解空间巨大等难题，本文以提高货架商品间关联性为目标，基于缩减问题解空间的思想，提出“关联网络构建→关联网络分析→关联网络聚类”的三阶段货位分配方法，将聚类的商品网络映射成货架对应的货位摆放来快速高效生成货位分配方案。利用某网上超市的实际数据，将所提方法与国内外普遍应用的几种方法进行对比，结果验证了所提方法的高效性和实用性，可为网上超市等企业采用机器人移动货架系统解决订单履行难题提供理论指导和决策支持。

关键词：机器人移动货架系统;货位分配;关联网络;聚类;“货到人”拣选模式

中圖分类号：C934 文献标识码：A 文章编号：2097-0145（2022）01-0056-09 doi：10.11847/fj.41.1.56

Abstract：As a new intelligent order picking system， the robotic mobile fulfillment system plays an important role in solving the multi-item orders picking problem faced by online supermarkets. The efficiency of this system hinges on the storage assignment procedure. However， due to the complexity of product correlation and huge solution space， this storage assignment procedure is difficult to optimize. In order to reduce the solution space for the problem of storage assignment in robotic mobile fulfillment system， a three-stage method of “association network construction→association network analysis→association network clustering” is proposed to improve the relevance of products on the rack. This method lays the foundation for solving the storage assignment problem quickly and efficiently by mapping clusters to racks. Using the order data of an online supermarket， this paper compares the proposed method with several widely used methods. Results verify the effectiveness and practicability of the proposed method. This research provides theoretical guidance and decision support for companies who employ this system to solve order fulfillment problems.

Key words：robotic mobile fulfillment system; storage assignment; association network; clustering; parts-to-picker picking mode

1 引言

随着互联网的快速发展，网上购物已经成为一种新型购物方式。中国拥有全球最大的网络零售市场，其中京东商城2020年成交总额达26125亿元，订单量仍在逐年递增，同时每一个订单平均包含7～8种商品[1]，传统“人到货”拣选模式面对订单量的爆炸式增长以及高比例的一单多品订单，导致仓库运营成本激增，仅订单拣选这一环节成本支出占仓库运营成本65%以上[2]。拣货员需执行高强度、远距离的重复性拣选操作，拣选效率低下。

基于AGV（Automatic Guided Vehicle， 自动导引小车）的机器人移动货架系统采用“货到人”拣选模式，在提升一单多品订单的拣选效率以及降低企业运营成本方面具有明显优势，已广泛应用于各大网上超市（京东商城、亚马逊）。然而，调研国内网上超市机器人移动货架系统发现，该系统在实际应用中存在拣货效率低等问题，究其原因，仓库管理人员仍然按照传统仓库的货位分配方法、并没有根据电商具有的一单多品订单、一货多位特点进行货位分配，导致机器人频繁搬运货架却只能拣选很少的商品，而履行一个订单通常又需要多个机器人搬运多个货架，根据调研统计发现，某电商仓库的订单平均购买3种商品，AGV平均花费6分钟搬运一个货架却仅仅拣选1.2种商品。这大大降低了该系统的运行效率。尽管电商也可以采取订单分批[3]、机器人调度[4]等方式提高系统拣货效率，但是由于货位分配是该系统首要关键性决策，如果货位未进行合理分配，后续再多的优化调度也是徒劳。因此，如何结合电商一单多品、一货多位的特点，研究机器人移动货架系统的货位分配问题，已经成为应用机器人移动货架系统亟需解决的关键难题。

传统货位分配研究主要集中于“人到货”拣选模式，“货到人”的机器人移动货架系统的货位分配作为新兴研究方向，是目前研究的热点难题[5]。由于传统货位分配基于货架摆放位置制定商品存储方案[6～9]，而机器人移动货架系统的货架位置不固定，因此传统货位分配方法的优势很难有效发挥[10]。近年，针对机器人移动货架系统的货位分配的相关研究刚刚起步，按照商品存储方式可划分为两种模式：一品一位[11～14]（一种商品仅存放一个货架），一品多位[15～19]（一种商品存放于多个货架）。

一品一位模式主要基于商品销量、商品间关联关系设计货位分配方法。代表性研究有：Lamballais等[11]以最大化系统吞吐量为目标，提出基于货架周转率的商品分区存储策略。Yuan等[12]考虑商品的周转率，以最小化货架移动次数为目标，提出一种基于销量的货位分配方式。Kim等[13]以最大化货架商品间关联度为目标，建立0-1整数规划模型，提出了一种构造启发式聚类算法。Li等[14]将共同购买频率高的商品存储在同一个货架，以最小化货架移动次数为目标，提出一种基于关联分析的聚类方法。上述研究基于销量、商品间关联关系进行货位分配，货架移动次数多，拣选商品数少，拣选效率不高，很难适用于一单多品订单的拣选。

一品多位模式可以根据商品的购买关联性进行一品多位的货位分配，更适用于机器人移动货架系统，能有效降低订单拣选时间，提高拣货效率[15]，正被大型网上超市等企业普遍应用。针对一品多位的货位分配问题，已有学者提出基于运筹学模型[16]和基于启发式算法[17]进行求解。代表性研究有：Guan和Li[16]针对商品的多货架分散存储需求，以最大化货架上商品间的关联度为目标，建立了货位分配的整数规划模型，并使用遗传算法求解该模型。李珍萍等[17]以搬运货架总时间最短为目标建立了货位分配的整数非线性规划模型，分别设计了求解该模型的贪婪算法和单亲进化遗传算法。Xiang等[18]以最大化货架上商品间的关联度为目标，建立了货位分配的混合整数规划模型，并调用CPLEX求解器进行求解。上述研究为求解这一难题进行了有益的探索，提供了新的定量分析模型和求解算法。但分析发现，机器人移动货架系统的货位分配是NP-hard问题，已有研究提出的方法仅可以求解小规模货位分配问题[17～19]，最多只能求解2000种商品，而实际企业运行的机器人移动货架系统往往需要考虑上万种商品的货位分配问题，导致已有的方法很难有效应用。同时，由于一单多品订单特点导致海量商品之间关联关系复杂，使得一品多位的货位分配问题更是难上加难。

本文针对机器人移动货架系统的一品多位货位分配问题，考虑一单多品订单带来的商品关联复杂性以及一品多位带来的解空间巨大等挑战性，基于缩减解空间的思想，以提高货架商品间关联性为突破口，提出“关联网络构建→关联网络分析→关联网络聚类”的三阶段货位分配方法。该方法通过将商品关联网络映射成多个类，每个类对应一个货架，频繁与多种商品组合购买的高关联度商品可被划分至多个类，可以巧妙化解海量关联商品的一品多位货位分配问题。该方法弥补了现有货位分配聚类方法仅能求解一品一位货位分配问题的不足，通过引入加权度筛选初始聚类中心，提出一种循环迭代聚类方法，可以对分配节点和剩余关联网络进行实时更新，不仅缩小节点的搜索空间，还实现了一品多位的存储需求、满足货架容量约束，解决大规模的一品多位货位分配问题，具备落地应用的可行性。利用企业的实际数据，验证本文方法的高效性和实用性，对商品存储货架数和货架容纳商品种类进行灵敏度分析。本文方法可为机器人移动货架系统一品多位货位分配方案的生成提供科学、实用的决策支持，对企业提升机器人移动货架系统的运行效率提供切实可行的指导意见。

2 问题描述与分析

2.1 问题描述

机器人移动货架系统是一种新型智能订单拣选系统，该系统采用“货到人”的拣选模式。该系统的拣选流程：AGV将存储有订单包含商品的货架搬运至拣选工作站，拣货员从货架拣选目标商品，拣选完成的货架再由AGV搬运至仓库的某个空闲存储位置。

机器人移动货架系统特别适合大型网上超市中体积小重量轻的小件商品的拣选，在电商仓库目前常采用的分品类存储模式下[20，21]，同一个机器人移动货架系统中通常只存放一个大类且体积较小的商品。由于订单拣选时，AGV会将整个货架搬运至拣选站，通过提升货架上商品间的关联性可以提高从每个货架可获取的目标商品数，从而有效提升拣选效率。机器人移动货架系统货位分配问题的决策一般是基于一段较长时间内的订单数据来分析商品间的关联性，这主要是由于短时间内的订单受促销等因素的影响，某些商品被人为增加了与其他商品购买的频率，产生噪声数据，与此同时，若根据一个季度的数据进行货位分配，可以有效进行季节性调整货位分配方案以适应顾客购买偏好的季节性变化。因此，基于一段较长时间（例如一个季度）的订单数据来挖掘稳定的商品购买关联关系，并将其应用于货位分配决策是增加货位分配结果鲁棒性、提升系统拣选效率的有效途径。

货位分配就是对货架上存储的商品种类进行优化，将商品存放在合适的货架以提升系统的揀选效率。假设仓库有N种商品，R个可移动货架，单个货架最多可存储M种商品，移动货架系统的货位分配需要决策各商品的存储货架，即把这N种商品摆放到R个货架上，且每个货架存储的商品种类数不超过M。在一品多位存储模式下，单种商品可在多个货架分散存储。顾客常同时购买多种商品，利用历史订单中商品组合购买的关联关系，可将顾客组合购买频率高的商品放在同一货架进行存储，通过增加货架上商品间的关联性，使得移动单个货架可拣选多种商品，从而减少总移动货架次数。故问题界定为如何将这N种商品摆放到R个货架上，使得货架的商品关联度总和最大。

基于多个机器人移动货架仓库的实地调研和文献梳理，提出如下假设：

（1）一个货架可以存储多种商品，单个货架可存储商品种类不超过最大种类数约束。

（2）一种商品可存放于多个货架。

（3）不考虑商品缺货的情况。

（4）基于一段较长时间（通常是一个季度）的历史订单进行货位分配决策。

为了便于后文表述，文中使用的变量符号及其代表的意义说明如下：

索引：

i， j表示商品的索引，i，j=1，2，3，…，N;

k表示订单的索引，k=1，2，3，…，K;

r表示货架的索引，r=1，2，3，…，R。

参数：

N表示商品种类数量;

K表示客户订单数量;

R表示货架数量;

M表示货架最大可存储商品种类数。

2.2 复杂性分析

通过对机器人移动货架系统货位分配问题的分析，发现该问题具有NP-hard特性，求解空间随问题规模增加而爆炸式增长，出现组合爆炸的情况，现证明如下：

定理1 “一品多位”存储模式下的机器人移动货架系统货位分配问题是NP-hard问题。

证明 当商品存储的货架数量设置为1时，“一品多位”存储模式下的机器人移动货架系统货位分配问题即变成“一品一位”存储环境下的机器人移动货架系统货位分配问题，该问题已被Mirzaei等[22]证明是NP-hard问题，因此，本文研究的“一品多位”存储模式下的机器人移动货架系统货位分配问题也是NP-hard问题。“一品多位”存储模式下的机器人移动货架系统货位分配问题的可行解比“一品一位”存储模式的解空间更大，求解更为复杂。对于一品一位和一品多位两种不同的货位分配模式，对比解空间大小是反映两者求解复杂性差异的有效手段。假定商品种类数目为N，单个货架最多允许存储M种商品，且N>M>1，不考虑货架空置，进行复杂性分析。

一品一位货位分配模式下，其中Z表示货架数量，Ω指所有可行解的集合，|Ω|表示解空间的元素数量，解空间内元素越多求解最优解的难度也越大。

由于N远大于M、x，解空间的元素数量主要受N影响，可固定M、x，分析N与解空间规模的关系。令x取最小值2，分析企业数据得知M最小为5，Z、Z′由（1）、（3）式计算得到。当N为6时，一品多位模式下的可行解数量是一品一位模式的15.3倍，而当N增长到23时，该数值已经达到了惊人的3.5×1019倍。更不用说，实际仓库的可移动货架数量可达上千、存储的商品种类在数万以上，在一品多位存储模式下，其可行解的数量十分庞大，难以用精确算法求解。因此，本文基于缩减解空间的思想，利用订单内商品的关联关系，提出基于商品关联网络的货位分配方法。

3 基于关联网络的三阶段货位分配方法

3.1 三阶段货位分配方法的求解原理

机器人移动货架系统一品多位货位分配问题面临两大难点：（1）问题可行解空间随商品种类数急剧膨胀。（2）一品多位货位分配引发的“商品-商品”与“商品-货架”关联关系复杂。针对这些难点，本文提出“关联网络构建→关联网络分析→关联网络聚类”的三阶段货位分配方法，该方法基于缩减问题解空间的思想，以提高货架商品间关联性为突破口，利用商品关联网络构建订单中商品的关联关系，通过分析关联网络中商品的加权度进一步对关联网络进行聚类，由于该方法可以将商品关联网络映射成多个类，每个类对应一个货架，从而巧妙化解海量关联商品的一品多位货位分配问题。

三阶段货位分配方法的核心内容如下：

（1）第一阶段为商品关联网络构建。针对海量多品订单的商品关联关系挖掘问题，将商品抽象成网络的节点，商品间两两组合购买的频次抽象成网络的边，这样构建的商品关联网络既能呈现商品间是否存在关联，又能表示其关联关系的强弱，从而将百万级订单信息压缩至数万种商品的关联，可以有效解决数量庞大、结构多样、一单多品订单给商品关联分析带来的时间和空间复杂度问题。

（2）第二阶段为商品关联网络分析。从整体拓扑结构、节点重要性、连边权重等维度对网络进行分析，利用网络呈现的高内聚、低耦合、无标度特性，将货位分配问题转化为聚类问题进行求解。同时，从网络节点加权度的角度，依据网络特性设计聚类求解方法，可大大缩减货位分配方案的解空间，有利于快速生成较优的货位分配方案。

（3）第三阶段为关联网络聚类。一品多位存储和货架容量有限的特点，使得用聚类求解货位分配时面临着单个节点出现在多个类、单个类节点总数约束等挑战。本文提出的关联网络聚类通过一种循环迭代聚类方式，可以对分配节点和剩余关联网络进行实时更新，不仅可以缩小节点的搜索空间，还可以实现一品多位的存储需求、满足货架容量约束。与此同时，该聚类方法引入加权度[23]筛选初始聚类中心，基于贪婪规则将关联性最强的节点归于一类，可以最大化同类节点的关联性。

3.2 阶段一：商品关联网络的构建

订单是挖掘商品关联性的重要依据，从订单内部结构来看，同一订单购买的商品种类、数量具有差异性，订单与订单之间由于购买相同的商品也会产生关联关系。数量庞大、结构多样、一单多品订单给商品关联分析带来时间和空间的复杂性。订单内部、订单间错综交叉的结构复杂性，本质是商品之间的关联关系，将订单中商品抽象成网络的节点，商品间两两组合购买的频次抽象成网络的边，这样构建的商品关联网络既能呈现商品之间是否存在关联关系，又能表示其关联关系的强弱，从而实现百万级订单信息压缩至数万种商品关联的转化，解决关联分析面临的时间和空间复杂性难题。商品关联网络的计算步骤如下：

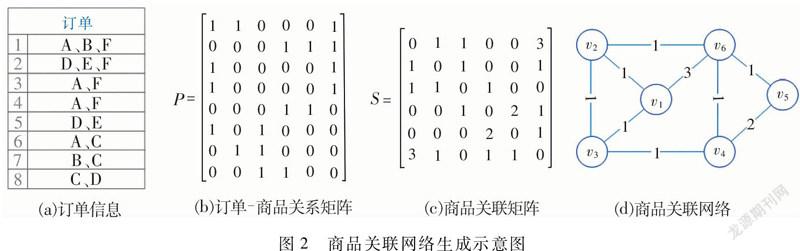
表1是一个客户订单的示例，以表中订单为例，介绍商品关联网络的构建流程。

图2是将订单信息转换成商品关联网络的图示，订单涉及的6种商品A到F分别被抽象成节点v1到v6。基于（8）式定义，根据图2（a）与表1一致的订单信息得到图2（b）的订单-商品关系矩阵P。根据（9）式，由订单-商品关系矩阵P计算可得商品关联矩阵S，相对应的商品关联网络如图2（d）所示。

3.3 阶段二：商品关联网络的分析

机器人移动货架系统一品多位貨位分配问题面临可行解空间随商品种类数急剧膨胀的难点，通过对商品关联网络的多维度分析，利用拓扑结构、节点、连边的分析结果指导货位分配问题求解，可使得货位分配结果匹配商品购买规律，大大缩减货位分配方案的解空间。基于国内某大型网上超市仓库的商品关联网络图，对网络结构、节点、连边的特征进行分析。

（1）拓扑结构分析

如图1（阶段二的子图）所示，从整体拓扑结构分析，商品关联网络具有高内聚、低耦合特征，聚类求解方式非常符合网络中商品节点聚集成团的特点，因此可以将货位分配问题转化成聚类问题进行求解，将节点聚成类，类对应货架，求解关联商品的货位分配问题。

（2）节点、连边分析

如图1（阶段二的子图）所示，从节点维度分析，网络的小部分节点与多个节点有连边关联，大部分节点仅连接少数节点，根据连边数量可知，节点具有差异性。从连边权重维度分析，权重取值也具有显著差异，部分连边权重仅为个位数，少部分连边的权重高于一千，连边权重代表商品一起购买的频次，不适合将不同权重的边视作同等重要。由节点重要性、连边权重分析可知，商品关联网络具有无标度特性，因此，通过优化关键核心商品的决策，可更高效地生成货位分配方案。

（3）节点加权度分析

结合节点重要性、连边权重的分析，加权度[23]适合用于度量商品关联网络节点的重要性，它是一种兼顾连边数量和连边权重差异的节点重要性度量方式，可筛选出频繁与多种商品一同购买的核心商品。计算步骤如下：

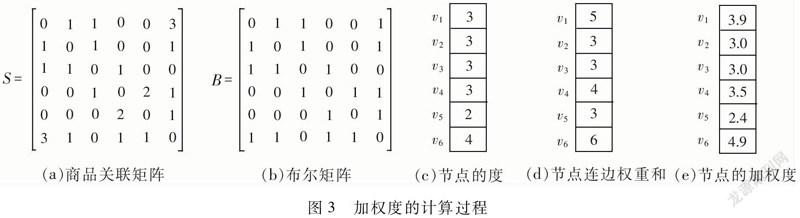
（1）计算布尔矩阵。为了计算各节点的加权度，先根据商品关联矩阵S计算布尔矩阵B，定义布尔矩阵

以图2的商品关联网络为例，图3展示了节点加权度的计算过程。第一步根据（10）式由商品关联矩阵S计算布尔矩阵B，结果如图3（b）所示。第二步根据（11）式计算各节点的度，结果如图3（c）所示。第三步计算各节点的加权度，先根据商品关联矩阵S计算节点的连边权重和，结果如图3（d）所示，再根据（12）式计算节点的加权度，结果如图3（e）所示。计算结果显示，加权度考虑连边权重差异，节点划分更加精确。例如，图3中节点v1、v2、v3、v4的度相等，但加权度将上述节点细分为三类，分别是加权度最大的v1，其次是v4，最后为v2、v3。

3.4 阶段三：基于关联网络的聚类算法

聚类将商品关联网络映射成多个类，每个类对应一个货架，一个节点可被聚到多个类，从而可以巧妙化解海量关联商品的一品多位货位分配问题，阶段二也详细阐述了聚类方式求解货位分配问题的有效性。传统聚类方法形成类的节点数量差异很大[25]，对应到仓库实际运营中，部分类不满足货架容量约束，货架存储空间的利用率差异很大，不具备可行性。现有机器人移动货架系统货位分配的聚类方法只能将节点聚到一个类，仅适用于一品一位货位分配问题的求解[13，14]。因此，本文提出基于关联网络的聚类算法，通过一种循环迭代聚类方式，可以对分配节点和剩余关联网络进行实时更新，不仅可以缩小节点的搜索空间，还可以实现一品多位的存储需求、满足货架容量约束。与此同时，该聚类方法引入加权度筛选初始聚类中心，基于贪婪规则将关联性最强的节点归于一类，可以最大化同类节点的关联性。算法伪代码如表2所示。

目前文献中效率最高的机器人移动货架系统货位分配聚类算法的时间复杂度为o（N4log N）[13]，本文算法的时间复杂度远低于已知最优算法，说明本文算法更加高效。

4 实例验证

实例验证分为两部分来度量提出算法的有效性，第一部分通过与不同算法的比较来分析算法计算结果，第二部分是对相应的参数进行灵敏度分析。基于沈阳某网上超市机器人移动货架系统的仓库配置，设定商品种类数为10005，单货架最多存储29种商品，拣选工作站5个，AGV为15台。本文构建了与该仓库对应的Flexsim仿真模型，通过Python 3.6编程实现货位分配算法，然后输入仿真模型对拣选效率进行对比。实验均在Intel Core I5-8265CPU， 1.80GHz， 8 GB RAM的计算机上求解。

4.1 结果分析

使用上述仓库2019年7月至9月的148015个订单，274875行购买记录，按比例划分训练集和测试集，训练集用于对货位分配方案进行训练，测试集可对训练得到的货位分配方案的优劣进行评估。整个季度的客户订单按照下单日期进行排序，日期早的客户订单排在前面、日期晚的排在后方，将时间占比80%的前74天的订单数据作为训练集，剩下20%的后18天的订单数据作为测试集。

针对机器人移动货架系统的货位分配问题，现有文献中方法有基于规则的分配方法[12]、启发式聚类算法[13]、遗传算法[16]、贪婪算法[17]，其中遗传算法和贪婪算法的问题求解规模受限，不进行比较，因此，本文主要是和构造启发式聚类算法、随机分配方法、按销量分配方法进行对比，其中构造启发式聚类算法是目前解决机器人移动货架系统货位分配最优的方法，该方法考虑商品的销量和商品间的购买关联关系提出了一种启发式聚类方法，以求解机器人移动货架系统的货位分配问题;随机分配方法作为基准算法，通过将商品随机放置于货架上来形成货位分配方案;按销量分配方法是当前仓库实践常用的方法，通过对商品按销量进行排序，将具有相同销量的商品放置于同一货架上。本文目标是最大化货架商品关联度总和，表3比较了各方法的货架商品关联度总和，以及仿真模型的运行结果。Imp%表示其他方法相对随机分配方法提升的百分比。

从表3可知，基于关联网络的货位分配方法显著提高了各货架商品间的关联度，比构造启发式聚类的结果高43.38%，比随机分配方法、按销量分配方法高21901.16%、922.54%，表明设计方法效果较好。本文方法在总搬运货架数、仿真拣选耗时、AGV行驶距离方面优势明显，均取得最小值，在AGV状态占比部分，本文算法的AGV空驶、空闲状态占比最低，载重状态占比最高，表明工作状态时间占比大，AGV利用率更高。总之，本文设计方法的仿真运行结果最好，其次是构造启发式聚类算法，再是按销量分配方法，随机分配方法的表现最差，各方法的表现结果与货架商品关联度总和的结果一致。其中与随机分配方法相比，本文所提方法能夠降低约33%的总搬运货架数和36%的AGV行驶距离。相比于目前表现最好的构造启发式聚类算法而言，本文所提方法依然可减少约10%的总搬运货架数和12%的AGV行驶距离。仿真结果进一步验证了本文方法的有效性，结果表明旨在增强各货架商品间关联性的货位分配是提高机器人移动货架系统拣选效率的有效方式。

4.2 灵敏度分析

4.2.1 商品存储货架数的分析

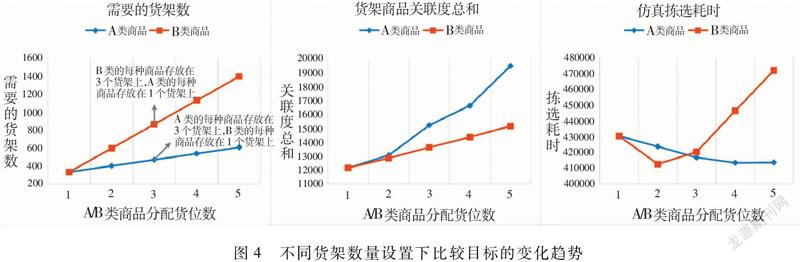
实践经验显示调整小部分商品存储的货架数量可大幅提高系统的拣选效率，本节用加权度来筛选这一部分商品，测试商品存储于不同数量的货架下拣选效率的变化。根据商品关联网络中节点的加权度，采用实践中常用的二八定律对商品分组，将商品划分为加权度值高的A类商品和加权度值低的B类商品（A类商品占比20%，B类商品占比80%）。货位分配采用基于关联网络的货位分配方法，分别修改A、B类商品存储的货架数量，图4展示了该组实验的结果。数据统计发现该仓库95%的商品存放的货架数量不多于5个，故至多允许5个货架存储同种商品，需要的货架数是满足当前货架数量配置所需的货架总数。

从图4可知，分别为A类、B类商品分配相同的存储货架数时，A类商品需投入的货架资源更少，但可实现更高的货架商品关联度总和，随着分配货位数的增加，A类商品在提升货架商品关联度方面的优势愈加明显。在仿真拣选耗时方面，前期B类商品投入1.5倍于A类商品的货架资源，通过增加货架成本，短暂取得拣选耗时的优势，后期即使为B类商品投入2倍以上于A类商品的货架资源，拣选耗时却明显处于劣势。分析发现，加权度值低的B类商品数量占比大，且不常与多种其他商品一起购买，为B类商品增加货架数时，货架商品关联度的增长慢，但需要面积更大的仓库和更多的货架，AGV必須行驶更远的距离以搬运货架，反而增加了拣选耗时。

4.2.2 货架存储商品种类数的分析

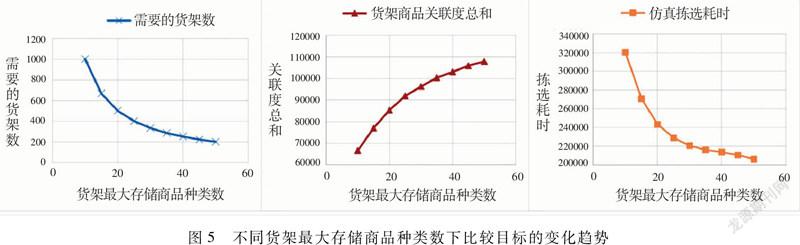
在生产实践中，企业十分关注单个货架应存放多少种商品。为了比较货架存储商品种类对拣选效率的影响，在不同的货架最多存储商品种类数下，采用基于关联网络的货位分配方法生成货位分配方案，分析了需要的货架数、货架商品关联度总和、仿真拣选耗时的变化，图5是实验结果。

由图5可知，随着货架最大存储商品种类数的增加，需要的货架数、仿真拣选耗时先快速下降，后缓慢减少，货架商品关联度总和也是先快速增长再缓慢增加。上述变化趋势显示，随着货架存储商品种类数的增加，拣选效率的增长速率下降，可以为企业根据拣选效率变化规律确定货架存储商品种类数提供决策支持。

4.2.3 管理启示

基于上述分析结果，从企业实践应用的角度出发，总结两点管理启示如下：

（1）根据实践中常用的二八定律，将加权度排名前20%的商品分散存放在一个以上的货架上，可以极大地提升系统拣选效率。加权度是度量商品重要性的有效方式，增加高加权度商品存储的货架数，拣选效率明显上升。网上超市在售商品种类多达数百万，单仓存储商品种类数万种，从企业经济成本和库存管理出发，不适宜为所有商品都分配多个货架。因此，企业可依据加权度进行货架资源分配，优先增加高加权度商品存储的货架数，最大幅度提高拣选效率。

（2）将货架商品关联度随货架存储商品种类数变化曲线的变化速率趋于稳定的点设置为货架最大存储商品种类数，可均衡拣选效率、补货成本和能源耗用。理论上讲，货架存储的商品越丰富，移动一个货架获得订单商品的概率越大。但是，货架存储商品种类越多，单种商品存放的量越少，导致频繁补货的问题，同时，货架存放过多商品使得AGV托举货架耗费的能源也越高，设置合理的货架存储商品种类数有利于系统高效地运行。分析拣选效率随货架存储商品种类数变化的变化趋势发现，增加货架存储商品种类数，拣选效率提升效果递减。因此，企业可参考该规律设置货架存储的商品种类数，实现拣选、补货和能耗的均衡。

5 结论与启示

针对机器人移动货架系统的一品多位货位分配难题，基于缩减解空间的思想，以提高货架商品间关联性为突破口，本文提出“关联网络构建→关联网络分析→关联网络聚类”的三阶段货位分配方法，第一阶段从订单中抽取商品关联关系构建商品关联网络，第二阶段分析网络结构后转化为聚类问题求解，第三阶段基于商品的加权度提出基于关联网络的聚类算法。研究成果为机器人移动货架系统货位分配的优化决策提供了一种新的求解思路，有助于丰富机器人移动货架系统的货位分配和启发式复杂网络聚类的成果。在实践上，理论成果为企业货位分配方案的生成提供借鉴。

本研究主要的贡献如下：（1）提出三阶段货位分配方法，利用网络高内聚、低耦合特征应用聚类方式求解，引入加权度提升聚类阶段质量，缩减问题的解空间，为货位分配方案的高效生成提供有效方法。（2）利用控制变量法分析商品存储货架数、货架存储商品种类数对拣选效率的影响，给出了管理启示，为企业划定货架容纳商品种类数、依据加权度的商品存储货架数分配提供了决策依据。

参 考 文 献：

[1] Zhang Y， Huang M， Hu X， et al.. Package consolidation approach to the split-order fulfillment problem of online supermarkets[J]. Journal of the Operational Research Society， 2017， 69（1）： 127-141.

[2] 李英德.波次分区拣货时装箱与货位指派问题协同优化的模型与算法[J].系统工程理论与实践，2013，33（5）：1269-1276.

[3] Boysen N， Briskorn D， Emde S. Parts-to-picker based order processing in a rack-moving mobile robots environment[J]. European Journal of Operational Research， 2017， 262（2）： 550-562.

[4] Gharehgozli A， Zaerpour N. Robot scheduling for pod retrieval in a robotic mobile fulfillment system[J]. Transportation Research Part E： Logistics and Transportation Review， 2020， 142： 102087.

[5] Azadeh K， De Koster R， Roy D. Robotized and automated warehouse systems： review and recent developments[J]. Transportation Science， 2019， 53（4）： 917-945.

[6] Heskett J L. Cube-per-order index-a key to warehouse stock location[J]. Transportation and Distribution Management， 1963， 3（1）： 27-31.

[7] Hausman W H， Schwarz L B， Graves S C. Optimal storage assignment in automatic warehousing systems[J]. Management Science， 1976， 22（6）： 629-638.

[8] 宁浪，张宏斌，张斌.面向JIT制造的零部件配送中心货位优化研究[J].管理科学学报，2014，17（11）：10-19.

[9] 田歆，罗春林，汪寿阳，等.零售物流中心运作优化的一種T型补货策略[J].中国管理科学，2018，26（4）：78-87.

[10] Weidinger F， Boysen N， Briskorn D. Storage assignment with rack-moving mobile robots in KIVA warehouses[J]. Transportation Science， 2018， 52（6）： 1479-1495.

[11] Lamballais T， Roy D， De Koster M B M. Estimating performance in a robotic mobile fulfillment system[J]. European Journal of Operational Research， 2017， 256（3）： 976-990.

[12] Yuan R， Graves S C， Cezik T. Velocity-based storage assignment in semi-automated storage systems[J]. Production and Operations Management， 2019， 28（2）： 354-373.

[13] Kim H J， Pais C， Shen Z J M. Item assignment problem in a robotic mobile fulfillment system[J]. IEEE Transactions on Automation Science and Engineering， 2020， 17（4）： 1854-1867.

[14] Li X， Hua G， Huang A， et al.. Storage assignment policy with awareness of energy consumption in the kiva mobile fulfilment system[J]. Transportation Research Part E： Logistics and Transportation Review， 2020， 144： 102158.

[15] Lamballais T， Roy D， De Koster R B M. Inventory allocation in robotic mobile fulfillment systems[J]. IISE Transactions， 2020， 52（1）： 1-17.

[16] Guan M， Li Z. Genetic Algorithm for scattered storage assignment in kiva mobile fulfillment system[J]. American Journal of Operations Research， 2018， 8（6）： 474-485.

[17] 李珍萍，范欣然，吴凌云.基于“货到人”拣选模式的储位分配问题研究[J].运筹与管理，2020，29（2）：1-11.

[18] Xiang X， Liu C， Miao L. Storage assignment and order batching problem in kiva mobile fulfilment system[J]. Engineering Optimization， 2018， 50（11）： 1941-1962.

[19] Chen L， Langevin A， Riopel D. The storage location assignment and interleaving problem in an automated storage/retrieval system with shared storage[J]. International Journal of Production Research， 2010， 48（4）： 991-1011.

[20] Zhang Y， Lin W H， Huang M， et al.. Multi-warehouse package consolidation for split orders in online retailing[J]. European Journal of Operational Research， 2021， 289（3）： 1040-1055.

[21] Zhu S， Hu X， Huang K， et al.. Optimization of product category allocation in multiple warehouses to minimize splitting of online supermarket customer orders[J]. European Journal of Operational Research， 2021， 290（2）： 556-571.

[22] Mirzaei M， Zaerpour N， de Koster R. The impact of integrated cluster-based storage allocation on parts-to-picker warehouse performance[J]. Transportation Research Part E： Logistics and Transportation Review， 2021， 146： 102207.

[23] Garas A， Schweitzer F， Havlin S. A k-shell decomposition method for weighted networks[J]. New Journal of Physics， 2012， 14（8）： 083030.

[24] Ding Z， Chen X， Dong Y， et al.. Consensus reaching in social network DeGroot model： the roles of the Self-confidence and node degree[J]. Information Sciences， 2019， 486： 62-72.

[25] Mangiameli P， Chen S K， West D. A comparison of SOM neural network and hierarchical clustering methods[J]. European Journal of Operational Research， 1996， 93（2）： 402-417.

[26] Kolen J F， Hutcheson T. Reducing the time complexity of the fuzzy c-means algorithm[J]. IEEE Transactions on Fuzzy Systems， 2002， 10（2）： 263-267.

3413500338239