Solid-liquid transition induced by the anisotropic diffusion of colloidal particles

Fu-Jun Lin(蔺福军) Jing-Jing Liao(廖晶晶) Jian-Chun Wu(吴建春) and Bao-Quan Ai(艾保全)

1Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,Guangdong-Hong Kong Joint Laboratory of Quantum Matter,School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China

2School of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China

Keywords: phase transition,anisotropic diffusion,colloidal particles

1. Introduction

Phase transition is ubiquitous in nature as well as in industry,and plays an essential role in statistical physics,materials science,chemistry,and biophysics. Physicists and mathematicians have long been fascinated by this issues. Understanding the phase transition kinetics and microscale processes is important not only for fundamental research,but also for applications associated with crystalline materials[1]and biotechnology.[2,3]Quantitative examinations on phase transition are mostly based on the models of repulsive hard spheres(discs),[4-8]charged spheres,[9-11]or attractive spheres.[12,13]As everyone knows,it is challenging experimentally to investigate the particles dynamics on an atomic or molecular scale.The colloidal particles,dispersing in a fluid medium,are larger than solvent molecules, but small enough to undergo Brownian motion. They are usually viewed as large atoms with tailorable sizes,shapes and interactions,[14]their thermal motion can be visualized by optical microscopy[15]and tracked by image processing.[16]Therefore, the colloidal suspensions have always been examined to understand the physical phenomena such as freezing, nucleation, melting, phase separation,structure formation, either spontaneous or driven by external fields.[17-22]The potential application of the spontaneous selfassembled of colloids can be selected as a promising route for fabrication of nanostructures,which requires us to deeply understand the relationship between their properties, structures and the self-organization processes.

The systematic studies mostly focus on the phase transition of the colloidal particles. Crystallization represents the prime example of a liquid-solid transition and has been extensively examined in many cases. Numerous types of crystals were revealed in simulations and experiments. A flowing crystalline structure, named rheocrystal, can spontaneously form by removing the particles,which is supported by numerical simulation and experiment.[23]However, a Monte Carlo ‘constrained aging’ method slows crystallization.[24]It is worth mentioning that an excellent work on crystallization of monodisperse self-propelled colloidal particles at sufficiently high densities has been carried out by Bialk´eet al.[18]They explored that the active colloids still freeze into a crystalline structure though the energy is injected incessantly,the freezing transition is largely shifted due to the selfpropulsion. Furthermore, the phase behavior in a system of binary hard spheres with different sizes has been reported in experiments[25,26]and theory.[27-29]The results indicate that the small spheres can fit between large spheres to stabilize binary crystals. The basic mechanisms of melting,spinodal decomposition, nucleation, and the glasses transition were performed in the past decades.

Most of the works on phase transition mentioned above mainly focus on spherical isotropic particles.However,perfect symmetry is an ideal case in nature. The anisotropy of particles, including the shape (e.g., ellipsoids, rods, or cubes), interaction(e.g.,janus)as well as diffusion anisotropy(e.g.,polar particles),is an intrinsic property. Specifically,anisotropic colloidal particles can be produced by tuning the shape of the particles, or putting the patches on the surface of the particles,also synthesized by two hemispheres with different properties. Indeed, studies on anisotropic particles have provided us with a wealth of insight into many microscopic kinetics and physical phenomena. The needle-like ellipsoidal particles under the action of an external potential exhibit complex motion and destroy the directed transport.[30,31]A variety of crystalline structures have been discovered by varying the shape anisotropy of spheroids.[32]However, phase transition behavior of spherical anisotropic particles has rarely been studied. In this paper, we study phase behavior of colloids with anisotropic diffusion and focus on finding how the diffusion anisotropy affects the solid-liquid transition.

2. Model and methods

We consider a suspension ofNparticles with diffusion anisotropy in two dimensions under periodic boundary conditions. Due to the particle anisotropy,the rotational and translational motions are always coupled in the lab-frame coordinates, which makes the analysis of relevant issues very complicated. For simplicity, we initially describe the motion of particle in body-fixed coordinates where the rotational and translational motions are decoupled. Then, the particle’s position vectorS(t) of its center of mass at a given timetcan be decomposed as (δ˜x,δ˜y), corresponding to the coordinates(δx,δy)in the lab frame. Here,θ(t)is the angle between thexaxis and the ˜xaxis. By means of a straightforward rotation of coordinates and a series of manipulations,the overdamped motion of theiparticle in Fig.1(b)can be written as[33,34]

whereDθ=kBT μ3is the rotational diffusion coefficient, describing the angular fluctuation. The superscripts of statistical averages in Eq. (5) mean over which the noises are averaged, and the subscript quantity is kept fixed. Defining Δμ ≡Δ ˜μ/¯μ ∈[0,1) to describe the anisotropy, the diffusion coefficient of the particle areD1=kBT μ1andD2=kBT μ2=[(1-Δμ)/(1+Δμ)]D1,respectively.

3. Numerical results and discussion

whereΠ(i) is the set of the six nearest neighbors of theith particle andθijis the angle between the vector from particleitojand an predefined direction. For a perfect crystalψ6=1, whereasψ6→0 in a disordered phase. Following Schweigertet al.,[37]the liquid-to-solid transition can be identified by a jump of the order parameter above a value ofψ6～=0.45. Meanwhile, a dynamical criterion for phase transition of the particles is determined by the abrupt drop of the long-time diffusion coefficient with Δri(t) =ri(t)-ri(0). The value of 0.086 forDhas been proved by L¨owen to be‘universal’,regardless of whether freezing occurs continuously via a hexagonal phase or is a conventional first-order transition,[38]thus we employ this criterion to describe the dynamical phase transition.

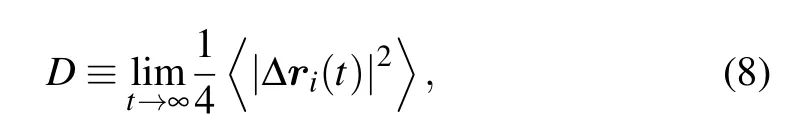
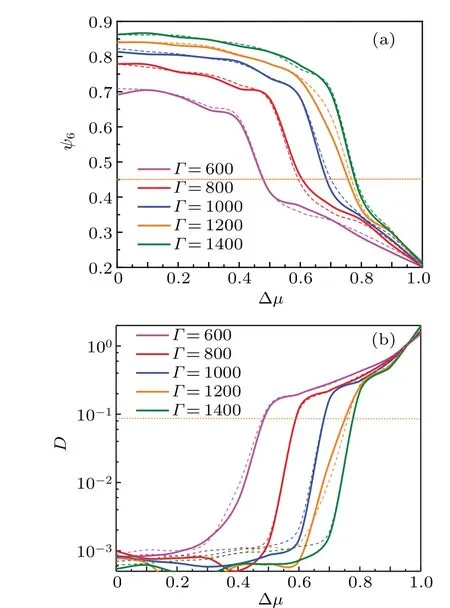
Fig. 2. Cooling curves (solid lines) and melting curves (dashed lines)for (a) the bond-orientational parameter ψ6 and (b) the long-time diffusion coefficient D versus the degree of diffusion anisotropy Δμ for different Γ. The crossings with the dashed horizontal lines define the position of the structural transition Δμ*S (ψ6=0.45)and the dynamical freezing Δμ*D (D=0.086),respectively.

We firstly examine the effect of the degree of diffusion anisotropy Δμon the phase transition by monitoring the global bond-orientational order parameterψ6and the long-time diffusion coefficientDfor differentΓin Fig.2. At the beginning of the simulation, a particle configuration with random particle positions and orientations is employed. From Fig. 2(a)we find that for a givenΓ,the particles can freeze into an ordered crystalline phase in the small Δμregion, especially for isotropic particles(Δμ=0),ψ6has its maximum value. With increasing Δμ, the Brownian diffusion along a specific axis of a particle becomes increasingly dominant,the random motion hinders the system from assembling an ordered structure.Therefore, the order parameter drops to belowψ6=0.45 at Δμ ≡Δμ*S, indicating a loss of the long-range orientational order in the system, and the system transits into the liquid phase.[39]Figure 2(b)exhibits dynamical phase transition for differentΓ, the diffusion coefficient increases abruptly near the phase transition point Δμ*D, which gives the lower bound to liquid region,and even exceeds that of a free passive Brownian particle. Obviously, the phase transition point is significantly shifted to the largeΓregion,which is determined by the competition between the degree of diffusion anisotropy and the coupling strength. As shown in Fig.3,with increasingΓ,the corresponding temperature of the system decreases,which leads to the dense colloids to gradually freeze into an ordered configuration and the diffusion coefficient to drop toward zero.

Fig.3. Cooling curves for(a)the bond-orientational parameter ψ6 and(b)the long-time diffusion coefficient D versus coupling strength Γ at Δμ =0.5.

Fig. 4. Snapshots of particle configurations for Δμ =0 (left column), 0.5 (middle column) and 0.9 (right column), the rows correspond to constant Γ,from top to bottom Γ =200(0.2886,0.2806,0.2014),700(0.7436,0.6160,0.2636)and 1400(0.8627,0.8128,0.2982). Particles are colored according to their ¯q6.

To assess in more detail the phase transition,we consider a process of melting starting from a perfect hexagonal crystal(dashed lines in Fig.2),and introduce the Lindemann-like parameter[41]

as a criterion to decide the upper bound to solid region. Here,the subscriptsiandjdenote two particles that are initially neighbors,and the lattice spacing of the hexagonal crystalℓ ≡21/23-1/4≃1.075. This criterion states that the melting commences once the vibrational displacement of a particle exceeds a certain fraction of the lattice spacing.[18]In our case, both the small coupling strength and large diffusion anisotropic degree can induce particles to vibrate sharply, the former has been explicated in Ref. [18]. We now mainly focus on the time dependence of the Lindemann-like parameter for different Δμat a givenΓ,e.g.,Γ=1000 as shown in Fig.5(a). It is found that,in the liquid region,the curves of the Lindemannlike parameter are abruptly divergent over time. Especially for Δμ ＞0.65,due to the existence of intensive diffusion in a special direction,the particles easily escape from their lattice position,and the crystal structure is destroyed. When Δμ=0.6,one can find a quasi-plateau with Lindemann-like parameterγL,we define this value Δμ*Las the melting point.Based on the above description, the phase diagram is mapped in Fig. 5(b).Clearly,the curves of Δμ*Sand Δμ*Dmostly coincide in all parameter space,which indicates that the two criterions we employed are compatible with our model. Note that in the region with largeΓand small Δμ,the particles crystalize into hexagonal structures, whereas in the smallΓor large Δμregion,the bond-orientational order is destroyed due to long-time diffusion. Moreover, there is a transition regime between liquid and solid,which is characterized by a high structural order and low but non-vanishing diffusion.[18]It is clear that the transition regime widens in the region of moderate parameter space,we regard it as the result of the competition between the degree of diffusion anisotropy and coupling strength, as shown in Fig.2.

We begin from briefly review our results to characterize the solid, liquid and transition regions. Figure 6(a)illustrates the probability distribution for ¯q6with differentΓat Δμ=0.5.One can find that the system is less structured in liquid region(Γ=200), while in the solid region (Γ=1400), the particles are well-crystallized with a few“bubbles”due to the longrange bond-orientational order. Notably,for the transition region(Γ=700),there is a broad peak probability distribution for ¯q6, corresponding to a coexistence phase as the second snapshot of middle column shown in Fig. 4. Figure 6(b) displays the probability distributions of ¯q6at Δμ=0,0.5 and 0.9 for four different globalψ6values. As has mentioned, when Δμ=0.9, the system is always disordered (ψ6＜0.3), thus there is only one curve. One can easily find that the probability distributions of ¯q6are less dependent on Δμ. It should be emphasized that a quasi-platform stretches across the distribution curve ofψ6=0.45,which means that the transition regime is occupied by a variety of heterogeneous structures.

Fig.6.Probability distributions of ¯q6(a)for different Γ at Δμ=0.5 and(b)at Δμ=0(solid line),0.5(dashed line)and 0.9(dot-dashed line)for four different global ψ6 values.

4. Concluding remarks

To summarize, we have numerically studied the solidliquid phase transition in a dense suspension of spherical colloids with different diffusions in an orthogonal direction.Starting from a random particle configuration,we have simulated the Langivin equations using the second-order stochastic Runge-Kutta algorithm in a two-dimensional box under periodic boundary conditions. The results show that the phase transition is strongly dependent on the diffusion anisotropy of colloidal particles. In the case of high temperature, a large diffusion anisotropic degree can induce particles to vibrate sharply, escape from the lattices, and destroy the long-range bond-orientational order. As a result, the process of crystallization is prevented. Furthermore, the strong-coupled particles with weak anisotropic diffusion can freeze into hexagonal crystals. By employing different criteria,the phase diagram in theΓ-Δμplane is obtained. It is clear that for a large Δμor smallΓregime,the system always keeps liquid phase. However,the particles with small Δμand largeΓare easily frozen into solid. There exists a transition region in which the suspension is overall ordered but with quite a few heterogeneous structures, which reflects as a broad-peak distribution for ¯q6.A competition between ΔμandΓwidens this region in the moderate parameter space.

Acknowledgements

Project supported in part by the National Natural Science Foundation of China (Grant Nos. 12075090, 11905086 and 12165015), the GDUPS (2016), and the Major Basic Research Project of Guangdong Province, China (Grant No. 2017KZDXM024), and the Natural Science Foundation of Jiangxi Province,China(Grant Nos.2021BAB201015 and GJJ200820),and Science and Technology Planning Project of Ganzhou City(Grant No.202101095077),and High-level Scientific Research Foundation for the Introduction of Talents of Jiangxi University of Science and Technology.