Persistent and enhanced spin-nematic squeezing in a spinor Bose-Einstein condensate

Xinfang LiJianning Liu, Osei Seth, Heng-Na Xiong,Qing-Shou Tan and Yixiao Huang,*

1 School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, China

2 School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China

3 Department of Applied Physics, Zhejiang University of Technology, Hangzhou 310023, China

4 School of Physics&Electronic Science,Hunan Institute of Science and Technology,Yueyang 414006,China

Abstract We propose a simple scheme to realize the persistent spin-nematic squeezing in a spinor Bose-Einstein condensate by rapidly turning-off the external magnetic field at a time that maximal spinnematic squeezing occurs.We observe that the optimal spin-nematic squeezing can be maintained in a nearly fixed direction.For a proper initial magnetic field, the optimal squeezing can be obviously enhanced.We further construct a spin-mixing interferometer, where the quantum correlation of the squeezed state (generated by our scheme) is fully utilized in the phase measurement,and show the phase sensitivity of the interferometer has a significant enhancement.

Keywords: quantum metrology, heisenberg limit, interferometry

1.Introduction

Spin squeezed state[1-3]has attracted considerable attention,both theoretically and experimentally due to the role in the fundamental study of particle correlation and many-particle entanglement[4-6].In the pioneering work[1],a scheme was proposed for the dynamical generation of spin-squeezed quantum states in an ensemble of spin-1/2 particles via nonlinear interaction between particles.Such a scheme is widely modeled as the so-called one-axis twisting which was implemented experimentally by utilizing interatomic interactions in two-component Bose-Einstein condensates (BECs)[7-19] and cavity-assisted setups [20, 21].Recently, the spin squeezing was generated in a spin-1 BECs, which is induced through spin-exchange interaction [22-36].For the spin-1 system,it possesses additional degrees of freedom associated with the nematic tensor operatorwith δijbeing the Kronecker delta and {i, j}∈{x, y, z}.The Hamiltonian of the system is conveniently written in terms of the spin and nematic-tensor operators that constitute the SU(3)Lie algebra,and the squeezing can be created via spinnematic correlation [37-43].However, the previous works mainly focused on the generation of the squeezed state itself.In practice, it is desirable to maintain and even enhance the squeezing due to its application to improve the precision of measurements in precise devices such as atomic clocks[44, 45], interferometers [46], magnetometers [47], etc.

Recently, nonlinear three-mode interferometers were realized in spinor BECs via spin-mixing dynamics(SMD)[48-55].The SMD consists of binary collisions that create or annihilate pairs of correlated particles and thus the squeezed state is generated within the interferometer.It allows phase measurements reaching a relatively high-precision.However, the previous protocols for the high-precision spin-mixing interferometer suffered one drawback because they did not make use of all the atomic particles within the phase measurement.A recent work proposed an alternative ‘pumped-up’ approach to use all particles to participate in the phase measurement and realized a quantum-enhanced measurement [56].However, the higher phase sensitivity that can be achieved in spinor interferometer is unknown.How to further improve the phase sensitivity is an important goal in the experimental frontier.

In this work, we propose a scheme for storage and enhancement of the spin-nematic squeezing in a spinor condensate with an external magnetic field.We consider all of the atoms initially prepared in the mf=0 mode.The SMD generates a spin-nematic squeezed state.We rapidly turn off the external magnetic field when the spin-nematic squeezing parameter attains its minimum.We observe the optimal spinnematic squeezing can be maintained in a nearly fixed direction along x-axis.We also show that the optimal squeezing can be enhanced when the initial magnetic field is larger than a critical value.For a proper initial magnetic field,optimal squeezing can even be increased by 4.5 dB.We further propose a spin-mixing interferometer in which the squeezed state’s quantum correlations is fully utilized, and thus the phase sensitivity of the interferometer has a great enhancement.Finally, we discuss the effect of the detection noise on the phase sensitivity.We show that the sensitivity of the output with the initial squeezed state generated by our protocol is better than that which is generated by the free evolution.

2.Model

We consider a spinor condensate with an external magnetic field, which has been realized in the experiment with cold atoms in an optical trap [25].The spin-dependent collisional interaction is typically much smaller than the independent one, and thus the single-mode approximation is expected to be valid which allows the different spin components of the condensate take the same spatial wave function [31].Under the single-mode approximation, the Hamiltonian for the spinor condensate can be written as [22, 57, 58]

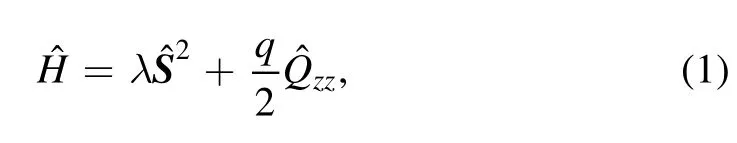
3.Spin-nematic squeezing

Unlike spin-1/2 atoms, in which the spin squeezing results from spin-spin correlation, the squeezing in the integer-spin systems can be induced by the spin-nematic correlation.The relative spin and nematic operators of the spin-1 BECs are defined as [22, 23]

In figure 1, we plot the spin-nematic squeezing parameteras a function of λt with different q.When q=0,the spin-nematic squeezing rapidly decreases to its minimum and disappears quickly.When q ≠0,the squeezing exhibits collapsed oscillations as shown by the dashed and solid curves in figure 1.It is shown the squeezing will not disappear which means the presence of the quadratic Zeeman energy protects the squeezing.In addition, the squeezing can also be enhanced with a proper quadratic Zeeman energy, such as q=25, as shown in figure 1 with the red solid line.However,the maximal squeezing cannot be maintained for a long time.

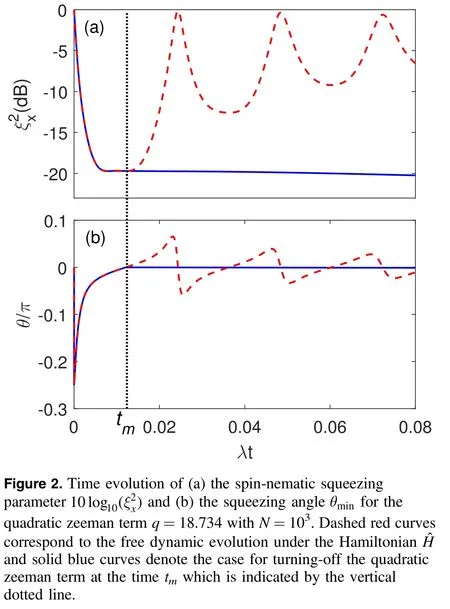
To store the maximal squeezing, we consider a two-step squeezing protocol.First let the initial state free dynamic evolution under the Hamiltonian,as shown in equation(1).Next turn off the quadratic Zeeman energy at a maximalsqueezing time, denoted as tm, that maximal spin squeezing occurs,and then allow the squeezed state to evolve under the HamiltonianSo the effective evolution operator of our protocol can be written asIn the following,we set the total squeezing time t=t2+tm.Experimentally,the SMD can be accurately controlled via microwave dressing[25].In figure 2(a), we plot the spin-nematic squeezing parameter as a function of λt with our protocol.It is shown the maximal squeezing can be stored for a long time.Moreover, it is stored in a fixed direction, i.e.θ ≈0, which means the squeezing direction is along the x axis, as shown in figure 2(b).For such a case, measuring the squeezing becomes easy.It only requires the squeezed state tomography involving one SU(3) rotations.A π/2 rotation about the Syaxis that rotates the fluctuations in Sxinto the measurement basis Sz.

The above result for the sudden transition of the optimal squeezing at the critical point can be understood by the squeezing angle of the optimal squeezing, denote as θopt,under the free evolution.In figure 3(c), we plot θoptas a function of q at tm.We find when q ≥qc, θopt=0, and thus the optimal squeezing is always along the x axis.It indicates that the minimal variance on the()plane isWhen we turn off the quadratic Zeeman energy,would be fixed in the dynamical process due to that the operatorcommutates withThus we can realize the storage and enhancement of the optimal squeezing.

The spin squeezing has been proved that it improved proofof-principle interferometric measurements.Here we show the spin-nematic squeezing parameter gives the metrological precision relative to the standard quantum limit for interferometer.In the following, we propose an interferometer with the spinor condensate and discuss the limit of the phase sensitivity.

4.Quantum metrology with spinor condensate

In fact, there are many other schemes of interferometer which also has a high precision, such as construct an interferometer via adiabatic transitions through quantum phase transitions and heralded mechanisms[53,62].The advantage for our produced scheme is that the preparation time of the squeezed state is much shorter than that generated by the adiabatic transition [61, 62].

5.Detection noise

Quantum-enhanced measurements typically require singleparticle resolution.However,the correlated state is fragility to the noise sources and thus limited the sensitivity of entanglement-enhanced metrology with squeezed state.A typical noise is detection noise which makes n and n+σ particles indistinguishable and leads the counting efficiency decrease.In the practical experiment, the detection noise in the spinor condensate arises mainly from the photon shot noise of the probing light [61].To describe finite detection efficiency we consider a Gaussian noise[63,64].The variance ofat the output state is then given by

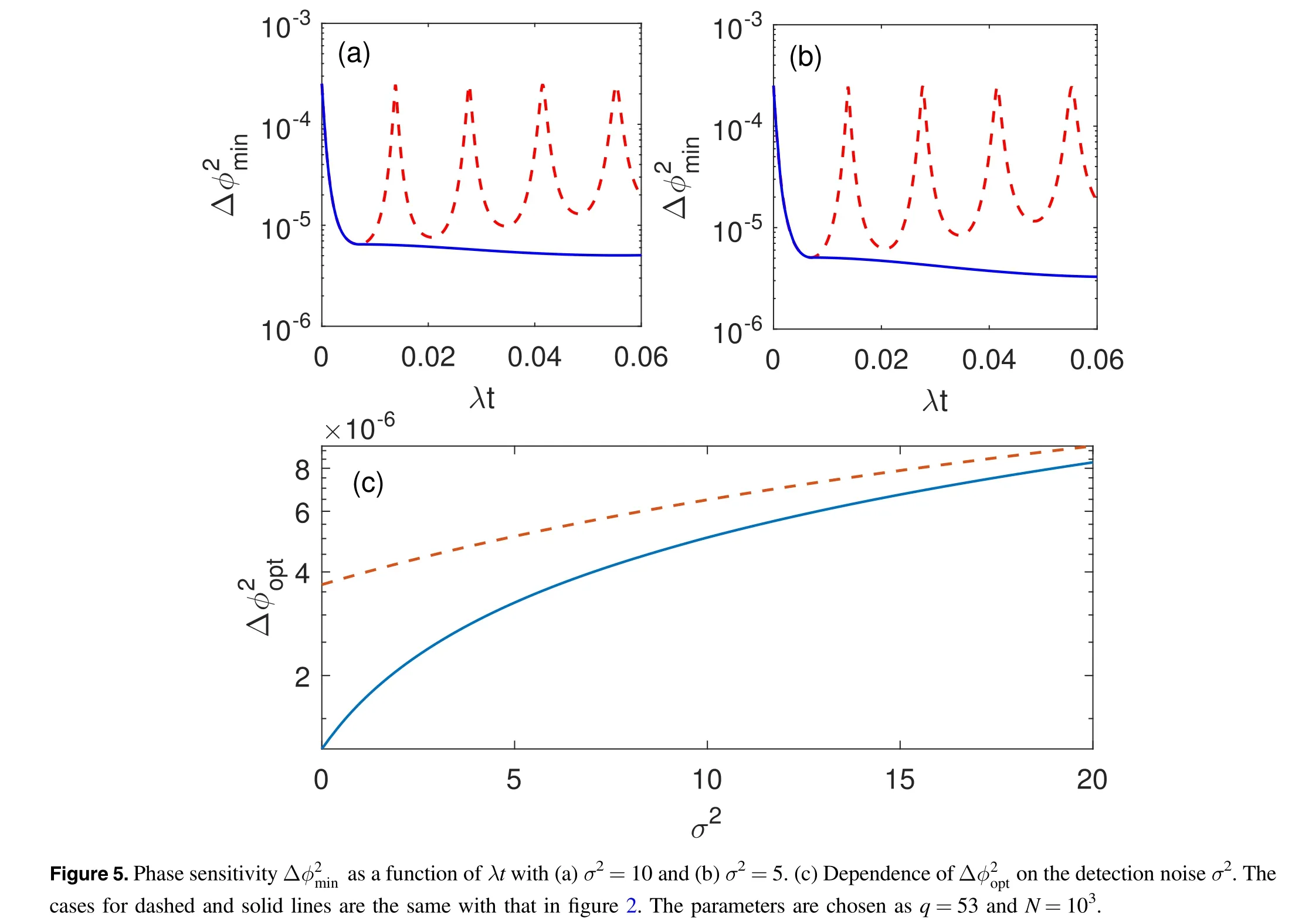
It results in the phase sensitivity

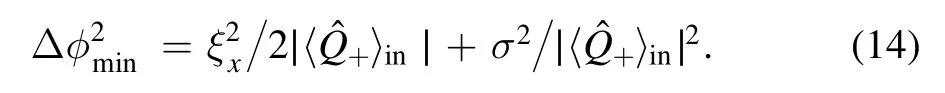
6.Conclusion

In summary,we have proposed a simple method to store and improve the spin-nematic squeezing in a spinor BEC condensate with an external magnetic field.By rapidly turning-off the magnetic field at the time when the maximal squeezing occurs, the spin-nematic squeezing is stored for a long time with a fixed direction along x-axis.Choosing a proper initial quadratic Zeeman energy, the optimal spinnematic squeezing can even be enhanced by 4.5 dB.We also propose an interferometer with the spinor condensate, and show that the phase sensitivity can be enhanced with our method which is presented for the improvement of spinnematic squeezing.Even in the presence of detection noise,the phase sensitivity of the interferometer with our method still has advantage compared to the free evolution.Our scheme for the enhancement of spin-nematic squeezing and phase sensitivity is quite robust for wide range of parameters.We hope our scheme will pave the way to atomic ultrasensitive spin-mixing interferometry in experiment near future.

Acknowledgments

We would like to thank HJ Xing for helpful discussions.This work was supported by the Natural Science Foundation of China through Grant No.11805047 and the Natural Science Foundation of Zhejiang Province through Grant No.LY22A050002.

ORCIDiDs