降低直流线路损耗的并联电容换相换流器单位功率因数控制策略
王晨欣,夏嘉航,赵成勇,郭春义
(新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
0 引言
由于能源的区域发展不平衡,基于电网换相换流器的高压直流(line commutated converter based high voltage direct current,LCC-HVDC)输电系统凭借其能够实现电网异步互联、远距离大容量输电、有功功率快速可控等优点,在工程中广泛应用,如“西电东送”“全国联网”等工程[1-2]。
电网换相换流器(line commutated converter,LCC)采用半控型的晶闸管作为换流器件,只能滞后触发,换流器消耗大量的无功功率,需要系统补充大量无功功率,导致LCC 交流侧滤波器组和无功补偿装置占地面积很大,而通过对交流滤波器和无功补偿电容进行分组投切,可以实现不同直流功率下系统的单位功率因数运行。此外,LCC 只能依靠电网进行换相,当逆变侧交流母线电压跌落时,逆变侧容易发生换相失败[3-6]。
合理控制系统与换流器的无功交换是降低换相失败概率和实现单位功率因数控制的关键。文献[7]提出一种静止无功补偿器(static var compensator,SVC)的优化设计方案及其新型控制策略,文献[8]提出在含有静止同步补偿器(static synchronous compensator,STATCOM)的高压直流输电系统中投入交流电压参考值调节功能、附加直流电流和附加关断角控制功能,文献[9]提出针对含有同步调相机(synchronous condenser,SC)的受端换流站多模式协调控制策略,三者均是通过提供无功支撑手段改善直流系统运行稳定性,抑制换相失败的发生,但是上述方法均依赖额外的无功补偿设备,并采用了较为复杂的控制策略,增大了设备投资成本,同时没有考虑实现全工况单位功率因数控制的情形。
电容换相换流器(capacitor commutated converter,CCC)通过投切交流侧无功补偿装置可以实现不同工况下的单位功率因数运行,增加的串联电容可以在一定程度上降低换相失败发生的概率[10];可控串联电容换流器(controlled series capacitor converter,CSCC)采用串联可控电容,使得CSCC 也可以通过改变可控电容大小调节换流阀和交流系统交换的无功功率[11-12],但CCC 和CSCC 在发生不对称故障时都可能引发过电压,加剧换相失败的发生,甚至引发连锁换相失败[13-15]。文献[16-18]提出了一种将全桥子模块串入换流阀和换流变压器之间的增强型电容换相换流器(enhanced capacitor commutated converter,ECCC),文献[19-21]提出了一种在原阀臂中串联接入新型可控子模块的改进型电网换相换流器(evolutional line commutated converter,ELCC),文献[22]提出了一种基于全控阻容模块(fully controlled resistancecapacitance module,FCRM)的LCC 拓扑方案,三者均可通过投切交流侧无功补偿装置实现不同工况下的单位功率因数运行,子模块的加入也可以减少换相过程,降低换相失败发生概率,但器件成本较高,子模块强迫换相能力有限,且无法进行滤波和大量无功补偿。
文献[23-25]提出一种吸收与并联电容换相换流器(absorption and shunt capacitance commutated converter,ASCCC),在换流阀出口侧和换流变压器之间并联三相电容,对交流谐波有一定的滤波作用,也降低了换相失败发生的概率。文献[26]提出了一种改进型并联电容换相换流器(evolutional shunt capacitor commutated converter,ESCCC) ,在ASCCC 的基础上,在并联电容和换流变压器之间增加了串联滤波电感,通过对滤波电感和并联电容的参数设计不仅改善了换流站交、直流谐波特性,还增强了系统抵御换相失败的能力。但ASCCC 和ESCCC 在轻载时,注入交流系统的无功功率升高,会导致无功功率过剩,功率因数降低;若仅考虑通过阀侧电容投切来实现单位功率因数控制,显然会影响换流器谐波特性。
针对以上问题,本文结合可在交流母线侧投切的并联补偿电容,并考虑直流线路损耗优化,提出一种基于ESCCC 的单位功率因数控制策略。本文首先分析了在交流母线侧并联补偿电容的ESCCC 拓扑结构和数学模型,研究了单位功率因数控制的原理,然后提出新型控制策略,根据新的谐波评价指标设计了换流器主要参数,并对投切电容方案进行了设计,最后在PSCAD/EMTDC 环境中搭建了相应的仿真模型进行验证。仿真结果表明新型控制不仅可以实现各工况下的单位功率因数运行,而且降低了直流线路损耗,同时保持了优良的交直流谐波特性和抵御换相失败的能力。
1 ESCCC 拓扑结构和数学模型
图1 为在交流母线侧并联可投切补偿电容器组的12 脉动ESCCC 结构示意图,采用的半导体开关器件均为晶闸管。12 脉动ESCCC 由2 个6 脉动换流器在交流侧并联、直流侧串联而成,阀交流侧出口先连接并联滤波电容C1,再连接串联滤波电感L0,之后分别经过各自的换流变压器(高压阀组为星形/三角形连接,低压阀组为星形/星形连接)后汇入交流母线,在交流母线侧并联有可以投切的补偿电容器组C2。
通过对图1 进行简化和等效,得到ESCCC 并联补偿电容的等效电路如图2 所示,其中各变量下标h、l 分别表示高、低压阀组,j表示j相单元(j=a,b,c),以高压阀组为例:i0h,j表示高压阀组出口侧j相交流电流;ih,j表示高压阀组经过电容滤波后的j相交流电流;ic1h,j表示高压阀组出口侧流经j相电容C1的交流电流;iph,j表示高压阀组通过变压器汇入交流母线的j相交流电流;ip,j表示流入交流系统的j相交流电流;uc1h,j表示高压阀组j相电容交流电压;up,j表示交流母线j相电压;Idc为直流电流;Udc为直流电压。
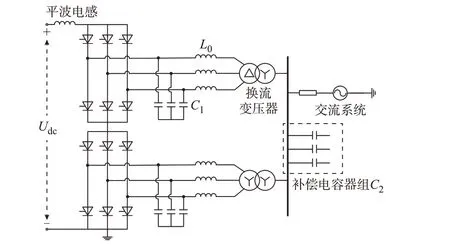
图1 12 脉动ESCCC 并联补偿电容结构Fig.1 Structure of 12-pulse ESCCC paralleled with compensation capacitor
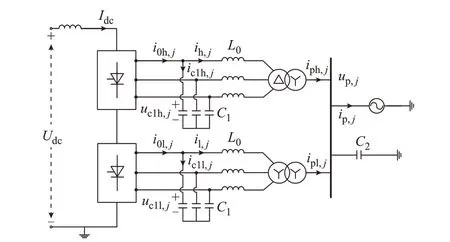
图2 12 脉动ESCCC 并联补偿电容等效电路Fig.2 Equivalent circuit of 12-pulse ESCCC paralleled with compensation capacitor
假设交流母线电压为Up,j∠0°,当触发角为α时,可计算得到高压阀组出口侧电流相量为:

式中:ω为交流系统角频率;İ0h,j、İh,j、İc1h,j、U̇c1h,j、U̇p,j、İph,j分别为i0h,j、ih,j、ic1h,j、uc1h,j、up,j、iph,j的相量形式;L为滤波电感L0和变压器漏感LT之和;k为变压器变比。

2 单位功率因数控制策略
以逆变侧为例,对交流母线电压进行锁相,结合式(5)和瞬时功率理论,可以得到流入交流系统的有功功率和无功功率为:

由式(7)可见,当交流母线电压Upm恒定时,可通过调节直流电流Idc、逆变站触发角αi、交流母线侧电容C2,实现对有功功率P的调节,以实现不同工况下的单位功率因数控制。
若不考虑交流母线侧电容C2的投切,可结合逆变侧系统参数,实现逆变侧ESCCC 的单位功率因数控制。单位功率因数控制策略框图详见附录A图A1,通过式(7)进行计算,将得到的直流电流Idc作为整流侧定电流控制的参考值信号Idc,ref,再经过比例-积分(PI)环节和限幅环节后得到整流侧触发角αr;将通过式(7)计算得到的触发角αi作为逆变侧触发角,进而生成触发脉冲。在不同的功率水平下,直流电流和逆变侧触发角的参考值都会随之改变,从而保证在各种工况下,换流站和交流系统之间传输的无功功率均为零,即实现单位功率因数控制。
然而,对于上述单位功率因数控制策略,轻载时逆变侧ESCCC 为了抵消换流阀侧并联电容发出的过量无功功率,需要大幅降低触发角αi来改善功率因数,这会导致轻载时直流电压下降幅度过大,直流线路损耗明显提高。
附录A 图A2 展示了当有功功率在0.1~1 p.u.变化时,单位功率因数控制策略下的直流电压和直流电流的变化关系。由图A2 可见,当传输功率降低时,直流电压会有较大幅度的下降,这会导致在传输相同有功功率时,直流电流会增加,使得直流线路损耗增大,同时也会导致逆变站在大关断角下运行,产生交直流谐波分量增大、器件损耗提升等一系列问题[1]。
为了解决轻载时直流损耗过高、直流电压下降较大等问题,可以在单位功率因数控制策略的基础上,重新设计滤波电感L0和滤波电容C1参数,同时在交流母线侧投切补偿电容C2。这不仅能保证满载时系统的无功功率和滤波需求,还能在轻载时提高直流母线电压,降低直流线路损耗。
3 参数设计
3.1 主体参数设计
为了满足控制要求,需要对滤波电感、滤波电容和补偿电容进行设计,设计的原则包括:1)在最小运行功率时,由于系统所需无功功率较少,考虑仅用换流阀侧并联电容提供无功功率,交流母线侧切除所有补偿电容;2)在额定功率时,由于系统无功需求增加,考虑交流母线侧投入所有补偿电容;3)在轻载时由于关断角增大,交直流谐波将比满载时大,因此只需保证ESCCC 在最小运行功率时有良好的交直流谐波特性即可;4)单位功率因数运行下,当系统运行功率小于额定功率时,直流电流应该比不采取投切电容方式时的直流电流小,以实现降低直流线路损耗的效果;5)在额定功率时有适当大的关断角(一般取为15°),从而实现全工况下关断角不低于15°。
为了对原则3)进行量化分析,本文采用文献[26]提出的谐波电流放大率kn来计算阀出口侧经过电容滤波后的交流电流n次谐波电流含有率khn,其中kn表示为:

当|khn|越小时,谐波电流含量越少。对于6 脉动换流阀,其交流侧特征谐波次数为6k±1 次,将|kh5|限制到比较小时,|khn|(n>5)就会更小,因此|kh5|可以作为谐振的重要指标。另外,|kh5|还影响流过变压器的谐波,为了避免铁磁谐振,|kh5|不能过大。
对于12 脉动ESCCC 换流器,流入交流系统的特征谐波次数为12k±1 次,谐波电流含量最大的谐波次数为11次,对于更高次的谐波其含量远小于11次谐波含量,因此取|kh11|作为评价交流谐波的指标。
为便于与LCC 的CIGRE 标准测试模型进行比较,采用与该模型相同的系统参数,以逆变侧为例,额定功率为1 000 MW 时,直流电压为500 kV,直流电流为2 kA,交流母线电压为230 kV,无功功率为0 Mvar。假定ESCCC 所能运行的最小功率为0.1 p.u.,即100 MW。
对于设计原则中关键指标的选取,具体采用以下参数。
1)针对原则3),当运行在最小功率0.1 p.u.时,参考IEEE 519—2014 标准中的谐波要求[27],取|kh11|=1%。
2)针对原则4),由于通常情况下降压运行方式的额定电压为额定直流电压的70%~80%[1],因此对于额定电压为500 kV 的系统,其降压运行方式的直流电压可取350~400 kV,而为了提高系统运行范围,取350 kV 为下限,得到P=0.1 p.u.下直流电流应为0.28 kA,计算方法如式(10)所示。
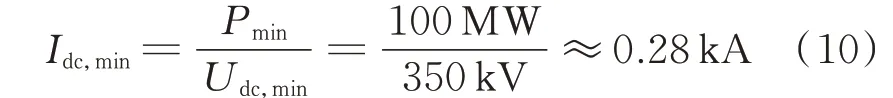
式中:Idc,min为直流电流下限;Pmin为有功功率下限;Udc,min为直流电压下限。
3)针对原则5),为了保证足够的关断角裕度,同时避免大量无功消耗,取关断角γ=15°。由于ESCCC 换相重叠角几乎为0°,因此可以认为触发角和关断角之和为180°,根据式(11)便可以得到触发角整定值αi。

根据以上条件,可以计算得到L=0.21 H,C1=5.08 μ F,变压器变比为230 kV/171.4 kV,此时100 MW 下的|kh5|=0.158,C2=9.81 μF。通过对交流母线并联可分组投切补偿电容的ESCCC 进行参数设计,不仅可以优化ESCCC 的交直流谐波特性,也为电容分组投切设计提供了依据。
3.2 电容分组投切设计
为了确定在不同有功功率下的网侧补偿电容投切方案,应考虑如下问题。
1)投切电容分组数。基于电容总容量一定的情况下分组越少,投资和占地越省的原则,参考典型无功补偿分组数[1,24-25],对于双极运行的12 脉动ESCCC,本文中选择分组数为6 组,正、负极分别布置1 个大组,每个大组分为3 个小组,对应3 组待投切的电容。在以下的分析中,仅以一极ESCCC 补偿方案为例。
2)第1 组投入电容功率点。由于换流器在P=0.1 p.u.工况下消耗无功功率较小,无须投入网侧补偿电容;但当有功功率升高到一定大小后,直流电压会超过额定电压,因此需要在直流电压未超过额定电压的功率点投入第1 组电容,并在合适的功率点投入第2 组、第3 组电容。为了尽可能降低直流线路损耗,原则上应保持直流电压尽可能大,才能使直流电流尽可能小,因此直流电压应尽量保持在1 p.u.,应选择在直流电压第1 次上升到1 p.u.时对应的有功功率点为第1 次投入电容的功率点。
3)投入电容后直流电压下限。电容投切会使系统运行状态发生变化,投入电容会使直流电压降低,切除电容会使直流电压升高。为了尽可能保持直流电压接近1 p.u.,每次投入电容时直流电压下降的幅度不能过大,且为了限制全工况范围内直流电压整体下降幅度,均衡考虑后,在每次投入电容后直流电压均应下降到同一数值,而每次切除电容后直流电压都上升到1 p.u.,以此为原则进行投切设计。
根据以上3 个考虑因素,可以得到3 种方案下直流电压和直流电流随有功功率的变化关系,如图3所示,其中:方案Ⅰ表示交流母线侧不投切电容的单位功率因数控制;方案Ⅱ表示理想的投切效果,即直流电压始终保持在1 p.u.,直流电流随有功功率呈线性变化,如在P=1 p.u.时直流电流为1 p.u.,在P=0.1 p.u.时直流电流为0.1 p.u.,但由于电容分组数有限,因此实际上无法达到方案Ⅱ的理想效果;方案Ⅲ则表示结合可在交流母线侧投切的并联补偿电容的单位功率因数控制。

图3 不同有功功率下直流电流和直流电压变化曲线Fig.3 Variation curves of DC current and DC voltage with different active power
从图3(a)可以看出,对于方案Ⅰ,若不采用有投切电容的单位功率因数控制,直流电流始终高于方案Ⅱ,在P=0.1 p.u.时直流电流约为0.275 p.u.,为方案Ⅱ的2.75 倍。而对于方案Ⅲ,其直流电流曲线与方案Ⅱ十分接近,在P=0.1 p.u.时直流电流为0.14 p.u.,与方案Ⅰ相比,直流电流降低了49.1%,直流损耗降低了74.1%;3 组投切电容的功率点分别为P0、P1和P2,在P0~P1、P1~P2和P2~1 p.u.这些区间内,方案Ⅲ的直流电流曲线分别在低功率点突变上升、在高功率点逐渐接近方案Ⅱ的理想曲线。由图3(b)可见,投切电容方案可以将直流电压限制在不超过额定电压水平,保留了足够的关断角裕度,维持系统正常稳定运行。
以ESCCC 所能运行的最小功率为100 MW、额定功率为1 000 MW 为例,通过上述分析可以计算得到各投切电容功率点和对应的投切电容大小,结果如下:1)第1 组投切电容功率点P0=391.55 MW,对应投切电容大小为2.32 μF;2)第2 组投切电容功率点P1=535.21 MW,对应投切电容大小为3.16 μF;3)第3 组投切电容功率点P2=731.58 MW,对应投切电容大小为4.33 μF。具体计算过程详见附录B。
通过计算也可以得到,每次投入电容后,直流电压均下降到486.06 kV,每次切除电容后直流电压会上升到500 kV,符合系统运行要求。
另外,ESCCC 还可以选择在阀出口侧对滤波电容进行投切的方案,从而实现单位功率因数控制。此时,根据上述相同的参数设计原则,可计算得出L=0.186 H,阀出口侧总并联电容为16.57 μF,换流变压器变比为230 kV/134.24 kV。
电容和电感的单位功率储能峰值在一定程度上可以反映体积和重量的大小[26]。LCC 方案和2 种基于ESCCC 的电容投切方案的电容、电感单位功率储能峰值对比如表1 所示,其具体计算方法见附录C。从表1 可以看出:基于ESCCC 的交流母线投切补偿电容的方案,其电容单位功率储能峰值为1.10 kJ/MVA,分别比LCC 方案和ESCCC 阀侧投切电容方案降低了45.5%和49.8%;而电感单位功率储能峰值为3.68 kJ/MVA,分别比LCC 方案和ESCCC 阀侧投切电容方案降低了9.8%和29.6%。因此,本文采用的方案在体积和重量上有较大的优势。
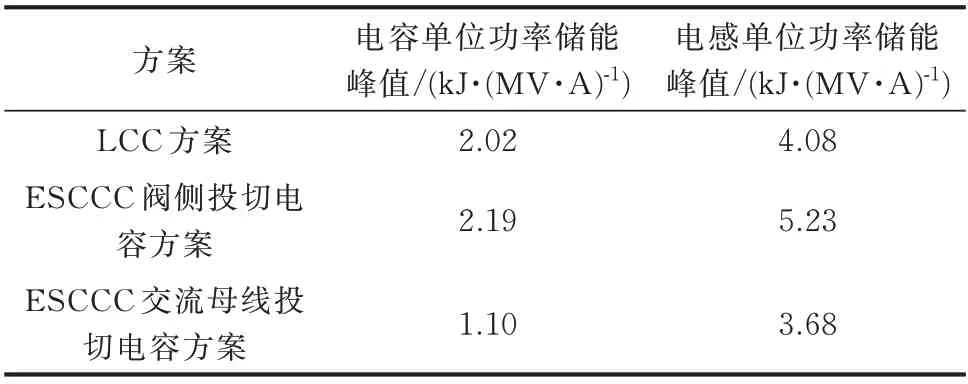
表1 各方案电容与电感参数对比Table 1 Comparison of capacitor and inductor parameters in different schemes
4 仿真验证
为了验证ESCCC 结合投切电容的单位功率因数控制策略的有效性以及参数设计的合理性,本文对如下4 个算例进行了仿真对比。
算例1:采用CIGRE 标准测试模型的LCCHVDC 系统。
算例2:采用定直流电压/电流控制的改进型并联电容换相换流器高压直流(ESCCC-HVDC)系统,其中逆变侧ESCCC 采用定直流电压控制,直流电压参考值为1 p.u.,整流侧采用定直流电流控制,不同工况下的直流电流参考值通过计算得出。
算例3:ESCCC-HVDC 系统,其ESCCC 采用文献[26]中的参数和本文第2 章所提的单位功率因数控制。
算例4:ESCCC-HVDC 系统,其ESCCC 采用结合在交流母线侧并联可投切电容的单位功率因数控制,具体参数为交流母线电压为230 kV,额定直流电压为500 kV,额定直流电流为2 kA,变压器变比为230 kV/171.4 kV,变压器漏抗为0.18 p.u.,滤波电感为0.182 H,滤波电容为5.08 μF,交流母线最大补偿电容为9.81 μF 。
算例1 至4 的基本参数均与CIGRE 标准测试模型相同,且均配备低压限流控制和最小触发角控制;算例2 至4 的整流侧参数一致。
4.1 单位功率因数控制仿真验证
为了观察单位功率因数控制对无功功率的控制能力以及投切电容对各电气量的影响效果,本节仅对算例2 至4 进行比较。
对全工况进行仿真分析,有功功率指令值随时间分段变化,变化过程如下:在1~1.5 s 时,有功功率参考值为100 MW;1.5~2.5 s 时,有功功率参考值从100 MW 线性上升至第1 次投切电容功率点P0,即391.55 MW 处,并在2.5~3.5 s 之间保持不变;3.5~4 s 时,有功功率参考值从391.55 MW 上升至第2 次投切电容功率点P1,即535.21 MW 处,并在4~5 s 之间保持不变;5~5.5 s 时,有功功率参考值从535.21 MW 上升至第3 次投切电容功率点P2,即731.58 MW 处,并在5.5~6.5 s 之间保持不变;6.5~7.0 s 时,有功功率参考值从731.58 MW 上升至1 000 MW,并在7~8 s 之间保持不变。对应的电容投入时间点如下:在3 s 处投入第1 组电容,容值为2.32 μF;在4.5 s 处投入第2 组电容,容值为3.16 μF;在6 s 时投入第3 组电容,容值为4.33 μF。3 个系统的各电气量仿真波形对比结果如图4 所示。
由图4(b)可以看出,算例2 至4 的有功功率均按照如图4(a)所示的指令值变化,算例4 中存在投切电容过程,所以在相应时间存在小幅度波动;由图4(c)可以看出,算例3 和算例4 采用的单位功率因数控制可以将无功功率限制在0 Mvar,而算例2由于未采用单位功率因数控制,无功功率不可控;由图4(d)至(f)可见,算例4 在3 个投切电容功率点投入电容之前,直流电流、直流电压、关断角和算例2接近,直流损耗小;当算例4 分别在3 s、4.5 s 和6 s投入电容后,直流电流小幅度上升,但始终不大于算例3 的直流电流,直流电压下降,使其始终不大于1 p.u.,关断角上升至20°左右,与理论分析结果基本相符。因此,结合补偿电容投切的单位功率因数控制的有效性和优越性得以验证。
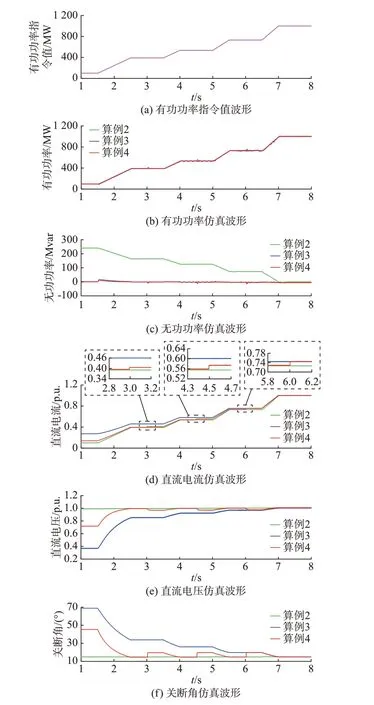
图4 不同工况下各电气量变化波形Fig.4 Waveforms of various electrical parameters under different working conditions
由于算例4 重新设计了逆变侧结构和参数,因此有必要对算例4 的谐波特性进行分析,其在额定工况下的直流电流、直流电压、网侧交流电流、网侧交流电压如附录A 图A3 所示。对图A3 仿真得出的波形进行傅里叶分析,结果表明逆变侧换流变压器网侧相电流和相电压波形畸变率分别为1.8%和0.08%,谐波特性良好,这验证了新型控制下新参数设计的合理性。
对网侧交流相电流和相电压进行频谱分析时,以基频50 Hz 作为参照,可以得到网侧相电流和相电压各次谐波含量如附录A 图A4 所示,由该图可以发现,各次谐波含量较低,谐波特性良好。
此外,在不同稳态工况下,以图4 的有功功率变化过程为例,分析投切电容对谐波特性的影响。
1)在最小运行工况下,交流母线侧不投入电容。通过傅里叶分析可以得到此时交流母线侧相电流和相电压波形的畸变率分别为2.44%和0.016%,但由于此工况下流入交流系统的交流电流基波幅值较小,约为0.35 kA,对应的各次谐波含量更小,因此对电能质量影响不大,而相电压的谐波畸变率则更低。
2)投入第1 组补偿电容:投入第1 组补偿电容前,交流母线相电流和相电压波形的畸变率分别为0.88%和0.025%;投入第1 组补偿电容后,交流母线相电流和相电压波形的畸变率分别为0.97%和0.027%。
3)投入第2 组补偿电容:投入第2 组补偿电容前,交流母线相电流和相电压波形的畸变率分别为0.92%和0.036%;投入第2 组补偿电容后,交流母线相电流和相电压波形的畸变率分别为1.1% 和0.037%。
4)投入第3 组补偿电容:投入第3 组补偿电容前,交流母线相电流和相电压波形的畸变率分别为1.3%和0.055%;投入第3 组补偿电容后,交流母线相电流和相电压波形的畸变率分别为1.40% 和0.057%。
综上所述,投切电容前后网侧交流相电流和相电压谐波畸变率变化幅度较小,因此基本可以忽略投切电容对谐波特性的影响。
4.2 动态性能比较
由于算例2 不能实现不同工况下的单位功率因数控制,因此仅对算例1、算例3 和算例4 在单相电感接地故障、三相电感接地故障2 种故障状态下进行仿真对比。
1)单相电感接地故障
t=2 s 时,在逆变侧交流母线设置经电感单相接地故障,接地电感为0.025 H,故障持续时间为0.1 s。将关断角降低到0°作为判断换流器发生换相失败的标准,可以得到3 个算例系统的动态性能比较如图5 所示。
结合图5 和对应换流器阀电流波形(详见附录A 图A5),算例4 各桥臂导通正常,关断角未降低至0°,未发生换相失败,算例1、3 在发生故障后,出现桥臂未正常关断、导通状态,对应关断角均降至0°,发生了换相失败。故障发生后,通过波形的比较,算例4 的直流电压、直流电流和交流母线电压几乎没有受到影响。相比之下,算例1 的直流电压几乎下降到了0 p.u.,直流电流上升到了2.5 p.u.,交流母线电压下降到了0.7 p.u.。而算例3 的直流电压下降到了0.2 p.u.,直流电流上升到了1.6 p.u.,交流母线电压下降到了0.8 p.u.。因此,与算例1、3 相比,算例4 系统抵御换相失败的能力更强,其故障恢复时间也比其余2 个算例更短。
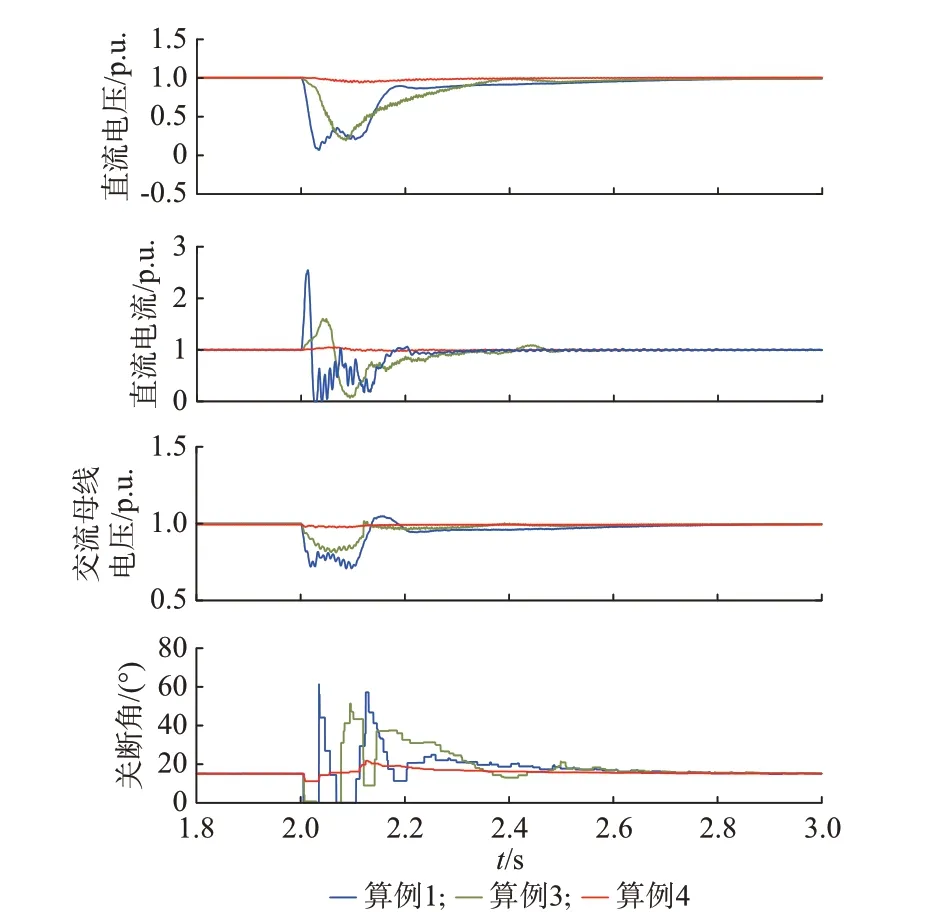
图5 单相电感接地故障下的仿真结果Fig.5 Simulation results with a single-phase inductance grounding fault
2)三相电感接地故障
t=2 s 时,在逆变侧交流母线设置经电感三相接地故障,接地电感为0.017 H,故障持续时间为0.1 s,可以得到3 个算例系统的动态性能比较如图6所示。
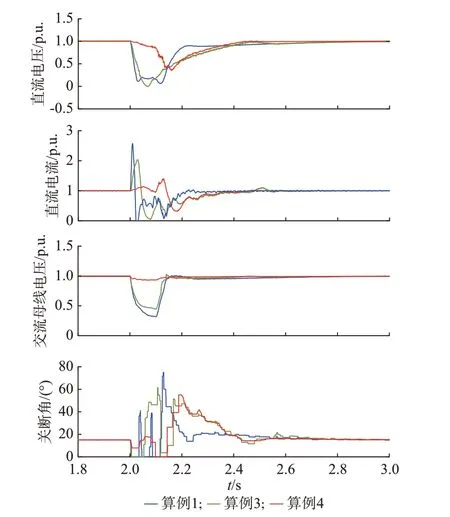
图6 三相电感接地故障下的仿真结果Fig.6 Simulation results with a three-phase inductance grounding fault
由图6 和对应换流器阀电流波形(详见附录A图A6)可见,3 个算例系统均出现桥臂未正常关断、导通现象,对应关断角均降至0°,发生了换相失败,其中算例1、3 的直流电压也近似降低到0 p.u.。算例1 的直流电流迅速上升到2.6 p.u.,算例3 的直流电流上升到2 p.u.,算例4 的直流电流上升到1.4 p.u.附近。算例1 的交流母线电压下降幅度最大,下降到0.3 p.u.,算例3 的交流母线电压下降到0.45 p.u.,而算例4 的交流母线电压虽然也有下降,但始终高于0.9 p.u.。故障消失后,3 个系统均可以顺利恢复正常运行。因此,算例4 具有较好的故障恢复特性,且仍然可以有效抑制故障电流的上升。
3 个算例系统在三相故障下的功率传输波形如附录A 图A7 所示,由该图可见,算例4 在发生故障后功率跌落较小,恢复速度快于算例3,并且在故障清除后可以更快回到额定功率水平,因此该控制对系统恢复和功率传输提升有所帮助。
4.3 换相失败概率的对比分析
为了进一步比较算例1、算例3 和算例4 抵御换相失败的能力,本文采用换相失败概率指标(CFPI)进行对比分析。
取交流电压的一个周期(0.02 s),将其平均分为100 份,即每2 个相邻故障点之间的时间间隔为20 ms/100=200 μs,在逆变侧交流母线处设置单相或三相电感接地故障,保持相同的接地电感和每次故障持续时间0.05 s,通过重复改变不同的故障投入时间,记录100 次投入中故障发生的次数并得到故障比例,即可得到该故障水平下的换相失败概率,最终将不同故障水平下的换相失败概率绘制成曲线。换相失败概率越低,说明系统抵御换相失败的能力越强。图7 为单相、三相电感接地故障下的换相失败概率曲线。
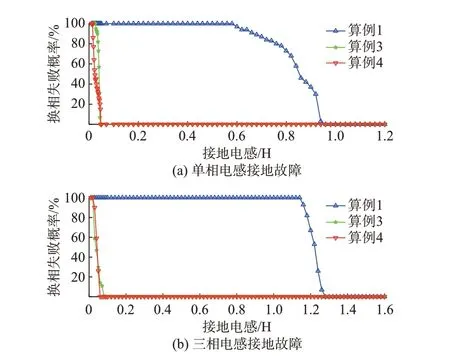
图7 单相、三相电感接地故障下的换相失败概率曲线Fig.7 Curves of commutation failure probability with single-phase and three-phase inductance grounding faults
由图7 可见,无论是发生单相电感接地故障还是三相电感接地故障,随着接地电感的降低,3 个算例发生换相失败的概率都会增大。换相失败概率曲线越靠下,表明相同故障水平下发生换相失败的概率就越低。由图7(a)可以看出,有投切电容的ESCCC 在单相电感接地故障下抵御换相失败的能力要好于没有投切电容的ESCCC;由图7(b)可以看出,有投切电容的ESCCC 在三相电感接地故障下抵御换相失败的能力与没有投切电容的ESCCC相差不大,且2 个算例在单相和三相电感接地故障下抵御换相失败能力均强于LCC。因此,采用结合投切电容的单位功率因数控制并重新设计系统参数后的ESCCC 抵御换相失败能力相比没有投切电容的ESCCC 有所提高。
5 结语
本文基于ESCCC 提出了一种结合在交流母线侧并联可投切补偿电容的单位功率因数控制,并设计了滤波电感、滤波电容和补偿电容等系统参数,分析了在不同功率点投切电容的方案。通过理论分析和仿真验证,得到以下结论:
1)在不同有功功率下,通过在交流母线侧投切不同的电容,可以实现不同工况下系统的单位功率因数控制,而通过投切电容可以保持直流电压始终不超过额定电压,同时降低了相同有功功率下的直流电流,即降低了直流损耗;
2)通过对滤波电感、滤波电容和补偿电容等参数的设计,使得系统仍然具有良好的交直流谐波特性,且投切补偿电容不会对谐波特性造成影响;
3)换相失败概率指标结果表明,新设计参数的带有投切电容的ESCCC 系统抵御换相失败的能力高于LCC 和没有设计投切电容的ESCCC 系统,即新型控制也改善了系统的暂态特性。
本文提出的单位功率因数控制方案具有一定优势,但在工程应用中仍需要进行后续的研究和完善,如在降低直流损耗的情况下进一步降低滤波电感体积的方法有待研究,双端闭环协调控制策略等问题也有待进一步研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

