氢气拉曼光谱压缩感知方法分析研究
任永甜,胡 仪,陈 骏,陈 钧
中国工程物理研究院表面物理与化学重点实验室,四川 绵阳 621908
引 言
气体分析应用广泛,关系到国计民生。无论是在科学研究中还是生产实践中,气体分析都有重要作用。气体成分分析的手段有气相色谱法、质谱法、红外光谱法、吸收光谱法和激光拉曼光谱法等。在光谱技术中,激光拉曼光谱具有非接触、无损等优点[1],但是,拉曼散射强度较低,实际测得的拉曼信号会受到射线、荧光、电荷耦合元件暗电流以及光学系统杂散光等干扰。为了提高信号质量,除了增加曝光时间或者提升硬件性能外,还可以利用信号处理技术对信号进行降噪处理。
目前用于光谱平滑降噪处理的方法有小波变换(wavelet transform)[2]、经验模态分解(empirical mode decomposition,EMD)[3]、Sawitzky-Golay(SG)滤波等[4]。但是在一些实际应用场景中,为了观察动态过程,信号测量时间较短,获得的信号的信噪比也比较低,而目前的一些降噪算法处理微弱信号的效果不是很好。除了小波去噪,常用于微弱信号检测的方法有盲源分离、相关检测、混沌检测和压缩感知(compressed sensing,CS)等。近年来,研究人员将压缩感知用于光谱的重建,取得不错的效果[5-6]。
氢气与我们的生活息息相关,氢气分析测量在国际热核聚变实验堆(international thermonuclear experimental reactor,ITER)、氢能等领域有重要意义。此外,氢气分子结构简单,是理想的研究模型。因此,本研究选取氢气和氘气作为测量对象,获取在采集时间较短情况下低信噪比的氢同位素气体拉曼光谱,研究压缩感知理论用于解析氢气拉曼光谱的可行性,并与其他降噪方法比对,结果表明压缩感知理论为氢气拉曼光谱降噪提供了一种有效的途径。
1 压缩感知重构与算法
2006年,Donoho,Candès,Romberg和Tao[7-9]等在研究信号稀疏性的时候发现只要一个信号是稀疏的或可压缩的,就可以通过合适的基或者框架对高维信号进行稀疏表示,然后使用高效算法从高度不完整的线性测量中恢复原始信号。可以通过更少的测量来感知稀疏信号,因此得名压缩感知。压缩感知不仅可以压缩采样,缩短采样时间,而且可以降噪,提高信噪比,以更好地实现原始信号的恢复和重建。压缩感知一般是由三个部分组成:信号的稀疏表示,信号测量和信号重构。
1.1 信号的稀疏表示
一个有限长一维离散信号x是RN空间N×1维的列向量,能够由N×N的稀疏矩阵Ψ表示为
x=Ψs
(1)
式(1)中,N×1的列向量s为信号x的稀疏系数,x如果仅有少数非零项,Ψ则是单位矩阵。除了傅里叶变换、小波变换等基函数,还可以用超完备的冗余字典稀疏表示数据。
本研究中两种压缩感知分析分别使用多组正交基构建的正交基字典和根据氢同位素气体拉曼光谱特征设计的字典。根据拉曼光谱中峰的强度和面积,设计洛伦兹函数线性组合F(x),F(x)作为纯净无噪声的拉曼信号,‖s‖0=K,由F(x)=Ψs可以得到稀疏矩阵Ψ。其中K表示稀疏度。
1.2 信号测量
通过M×N维的测量矩阵Φ与信号x做内积,得到测量值y,因为M远远小于N,所以可以减少测量数据量,达到降维的目的。测量值y可以写成
y=Φx+e=ΦΨs+e=Θs+e
(2)
式(2)中,y为M×1的列向量,Θ=ΦΨ为M×N的传感矩阵,e表示有界能量的噪声项[8],‖e‖2≤ε。
1.3 信号的重构及重构算法
信号的重构可以转换为l1最小范数下的最优化问题
min‖x‖1s.t.‖y-Φx‖2≤ε
(3)
本研究选取正交匹配追踪(orthogonal matching pursuit,OMP)[10-11]算法对氢同位素气体拉曼光谱信号进行重构,OMP算法步骤如下:
输入:M×N维的传感矩阵Θ=ΦΨ,M×1的测量值y,信号稀疏度K。
在算法中,用∅表示空集,Λt表示t次迭代的索引的集合,Jt表示t次迭代的索引号。
初始化:残差r0=y,索引集Λt=∅,Θ0=∅,迭代次数t=1。
循环执行步骤(1)—步骤(5):
(1)找出残差rt-1和传感矩阵Θj内积中的最大值,即找索引Jt,使得Jt=argmaxj=1,2,…,n|〈rt-1,Θj〉|,其中,Θj是传感矩阵第j列;
(2)更新索引集Λt=Λt-1∪{Jt},记录找到的传感矩阵中的重建原子集合Dt=[Dt-1,ΘJt];
(5)令t=t+1,若t 本研究选用H2(氕)和D2(氘)组成的氢气作为研究对象,基于压缩感知理论,①对拉曼光谱傅里叶变换,带阻滤波后反变换回到时域,并结合多组正交基构建正交基字典,用OMP算法(下文简称FTOMP)对拉曼光谱进行重构;②对拉曼光谱进行寻峰和多项式拟合基线[12],然后通过洛伦兹函数设计原子,构造字典,用OMP算法(下文简称LoOMP)对拉曼光谱进行重构。并与小波软阈值、小波硬阈值和SG滤波处理结果比对,分析几种方法处理后的信噪比和均方根误差。 首先进行了仿真实验,使用洛伦兹函数来仿真纯净的拉曼光谱信号。为了仿真弱拉曼光谱信号,仿真信号设计的强度较低,每个峰的信号强度均不超过20。仿真信号峰的位置、峰的强度和峰的半高宽等相关参数如表1所示。图1(a)为仿真的无噪声拉曼光谱。 表1 仿真信号参数表Table 1 Parameters of only simulated Raman signal 图1 (a)无噪声的仿真光谱;(b)加入噪声的仿真光谱;(c)FTOMP重构的光谱;(d)LoOMP重构的光谱;(e)小波软阈值降噪的光谱;(f)小波硬阈值降噪的光谱;(g)经SG滤波的光谱Fig.1 (a)Simulated spectrum;(b)Simulated spectrum with noise;(c)Reconstructed spectrum by FTOMP;(d)Reconstructed spectrum by LoOMP;(e)Denoising spectrum with Wavelet soft threshold;(f)Denoising spectrum with Wavelet hard threshold;(g)SG filtered spectrum 为了测试压缩感知算法的降噪能力,对图1(a)中无噪声的仿真光谱信号加入5 db高斯噪声。然后使用几种方法对含噪声谱图进行处理,图1(b)为加入5 db高斯白噪声后的仿真拉曼光谱,图1(c)为FTOMP算法的重构光谱,图1(d)为LoOMP算法的重构光谱,图1(e)为小波软阈值处理得到的降噪光谱,图1(f)为小波硬阈值处理得到的降噪光谱,图1(g)为经SG滤波获得的降噪光谱。其中使用LoOMP算法重构的拉曼光谱的参数信息如表2所示。 表2 LoOMP重构信号的参数Table 2 Parameters of reconstructed Raman signals by LoOMP 并通过计算降噪后的信噪比(SNR)和均方根误差(RMSE)以及谱峰强度偏差(Intensity error)这三个指标对降噪效果进行评价,表达式分别如式(4)—式(6) (4) (5) (6) 图2 压缩感知方法重构信号(a):M/N-SNR曲线;(b):M/N-RMSE曲线;(c):K-SNR曲线;(d):K-RMSE曲线Fig.2 Compressed sensing method to reconstruct the signal(a):M/N-SNR curves;(b):M/N-RMSE curves;(c):K-SNR curves;(d):K-RMSE curves 表3 含噪声的仿真光谱处理前后的SNR和RMSETable 3 SNR and RMSE before and after processing the treatments of the simulated noisy Raman spectrum 实验采用自制拉曼光谱仪对氢气同位素气体进行测量,激光波长为532 nm。样品池中充入氢气和氘气的混合气体,光谱采集时间分别为1,0.15,0.10,0.08,0.06,0.05和0.04 s。其中1 s采集的拉曼光谱如图3所示。图中4 163和2 993 cm-1处的谱峰分别为H2和D2的Q1支振动信号。 图3 1 s采集的H2和D2混合气体的拉曼光谱Fig.3 Raman spectrum of H2 and D2 mixed gas with 1 s collection time 以0.1 s拉曼光谱作为处理对象,并对其进行归一化处理,比较五种方法降噪处理后的谱图,如图4所示,图4(a)是0.1 s采集的H2和D2混合气体的拉曼光谱,图4(b)是FTOMP算法重构的光谱,图4(c)是LoOMP算法重构的光谱,图4(d)是小波软阈值降噪后的光谱,图4(e)是小波硬阈值降噪后的光谱,图4(f)是经SG滤波降噪后的光谱。从谱图上可以看出,LoOMP重构处理的谱图曲线最光滑。五种方法处理后,拉曼光谱中D2信号的谱峰强度与同一采集时间下连续采集100次拉曼光谱得到的平均谱作比较,得到D2信号强度偏差如表4所示。然后计算了FTOMP重构后的光谱与LoOMP重构后的光谱在不同采样率M/N和稀疏度K下D2信号的谱峰强度偏差,结果如图5所示,M表示测量值,N表示信号的长度。 图4 (a)0.1 s采集的H2和D2混合气体的拉曼光谱;(b)FTOMP重构的光谱;(c)LoOMP重构的光谱; (d)小波软阈值降噪的光谱;(e)小波硬阈值降噪的光谱;(f)经SG滤波的光谱Fig.4 (a)Raman spectrum of H2 and D2 mixed gas with 1 s collection time;(b)Reconstructed spectrum by FTOMP;(c)Reconstructed spectrum by LoOMP;(d)Denoising spectrum by Wavelet soft threshold;(e)Denoising spectrum by Wavelet hard threshold;(f)SG filtered spectrum 表4 五种方法处理后拉曼光谱中D2信号的谱峰强度偏差Table 4 The difference in the D2 signal intensity by the five methods 图5 两种压缩感知方法处理后光谱中D2信号的强度偏差(a):信号强度偏差与采样率M/N的关系曲线;(b):信号强度偏差与稀疏度K的关系曲线Fig.5 The difference in the D2 signal intensity by LoOMP and FTOMP(a):Intensity error of D2 signal vs M/N value;(b):Intensity error of D2 signal vs K value 六组采集时间下的拉曼光谱经过几种方法处理得到的谱图在D2信号处的强度如图6(a)所示,图6(b)是五种方法处理后D2信号处的强度偏差。 图6 五种方法处理的拉曼光谱中D2信号(a):谱峰强度与采集时间的关系曲线;(b):谱峰强度偏差与采集时间的关系曲线Fig.6 The difference in the D2 signal intensity by LoOMP and FTOMP(a):Intensity of D2 signal vs collection time;(b):Intensity error of D2 signal vs collection time 从表1—表3以及图1可以看出,几种方法处理后光谱的信噪比均有所提高,均方根误差减小。本研究提出的LoOMP算法能够很好地重构拉曼光谱的拉曼峰,获得的谱图的信噪比最大,均方根误差最小,其次是小波软阈值处理后的光谱,FTOMP算法重构光谱与SG滤波降噪光谱的信噪比最低,均方根误差最大。当M/N=0.8,K=50时,FTOMP算法重构谱图的信噪比为10.274 8,均方根误差为0.877 1,比LoOMP重构效果差。通过仿真实验可知LoOMP算法处理拉曼光谱的降噪效果相对最优。 图2探究了采样率和稀疏度对压缩感知算法重构信号效果的影响。随着采样率的增大,LoOMP算法重构光谱的SNR和RMSE变化较小;当M/N达到0.4~0.5时,FTOMP的重构效果达到最佳,SNR和RMSE随M/N变化趋于稳定;随着稀疏度的增大,两种压缩感知算法重构光谱的SNR和RMSE增大,当K=50时,此时SNR和RMSE最佳,并且随着K的增加趋于稳定。比较LoOMP算法和FTOMP算法重构光谱的SNR和RMSE,LoOMP算法重构效果要好。 结合图4和表4,可以看出,实验数据和仿真结果一致,LoOMP算法在拉曼峰处重构效果最佳,谱峰强度偏差最小,降噪效果最好;小波软阈值降噪效果较好,但是在拉曼峰处强度偏差较大;小波硬阈值和SG滤波处理结果在拉曼峰处强度偏差居中,但是降噪效果较差;FTOMP处理效果最差。 图5展示了随着采样率和稀疏度的变化,拉曼峰强度的重构偏差结果。随着采样率的增大,强度偏差变化趋势较小,LoOMP的强度偏差要比FTOMP小得多;随着稀疏度的增大,强度偏差在减小,LoOMP算法重构光谱的谱峰强度偏差比FTOMP算法小很多,可以得出LoOMP算法相对FTOMP算法重构的信号效果要好。图6是不同采集时间下的拉曼光谱经过几种方法重构后D2信号的强度的变化以及偏差。可以看出,LoOMP重构谱峰强度和原始光谱谱峰强度偏差最小,且相对稳定;小波硬阈值和SG滤波两种方法在谱峰处重构效果较好;小波软阈值和FTOMP在谱峰处重构强度偏差较大。但是在采集时间较长情况下小波软阈值重构效果好于FTOMP。 LoOMP和FTOMP两种压缩感知算法的处理结果差别较大,主要原因是LoOMP根据拉曼光谱特征,使用洛伦兹函数构建字典的原子,这样可以更好地保留光谱特性,该方法适用于拉曼光谱的降噪,可以恢复拉曼光谱的特定主峰,其效率在某些方面优于其他方法,对评价拉曼光谱和检测被测物具有重要意义,在安检等一些需要定性分析场景中具有一定的应用价值;FTOMP使用正交基构建的字典对拉曼光谱稀疏表示效果较差,而且经过傅里叶滤波处理,谱峰强度会有所降低。 将压缩感知用于拉曼光谱重构的工作,重构拉曼光谱信号峰的频率、峰宽和强度[13],可以扫描几个光谱基[14],也可以减少信号采集时间[5]。本研究与现有的降噪方法相比,主要是将压缩感知算法应用于氢气拉曼光谱降噪处理,结合氢气拉曼光谱信号特征,使用洛伦兹函数设计稀疏矩阵的原子,可以更好地稀疏表示原始拉曼光谱数据,以达到在重构过程中对氢气拉曼光谱降噪的目的。而且LoOMP算法处理氢气拉曼光谱的时候不需要对拉曼光谱进行分段处理,可实现直接对几个拉曼峰同时重构,降噪的同时还保留了拉曼信号的强度和谱峰基本形状信息。 运用压缩感知算法分析氢同位素气体的拉曼光谱,研究两种不同的稀疏矩阵构建方式对重构结果的影响。通过对仿真光谱和实际测量拉曼光谱进行处理比对,研究表明:提出的LoOMP压缩感知算法可以有效地降低噪声,同时信号强度偏差很小。通过比对,LoOMP压缩感知算法重构的氢同位素气体拉曼光谱的信噪比和均方根误差优于FTOMP压缩感知算法、小波软阈值法、小波硬阈值法和SG滤波方法,且拉曼峰的强度重构偏差最小。鉴于气体拉曼信号特征相似,本研究的LoOMP压缩感知算法也适用于其他气体的拉曼光谱的降噪处理。2 实验部分
2.1 仿真数据处理



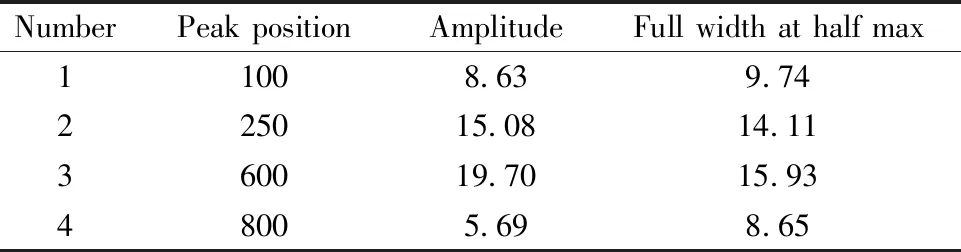



2.2 实际测量数据处理




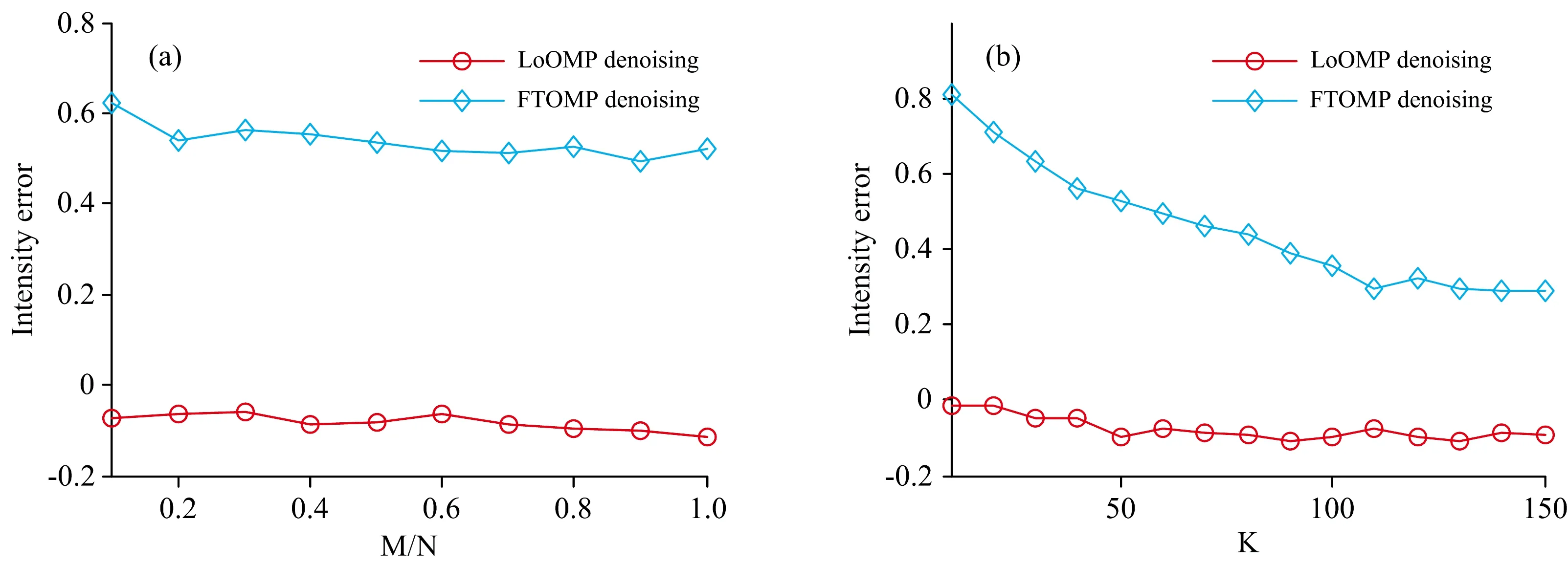
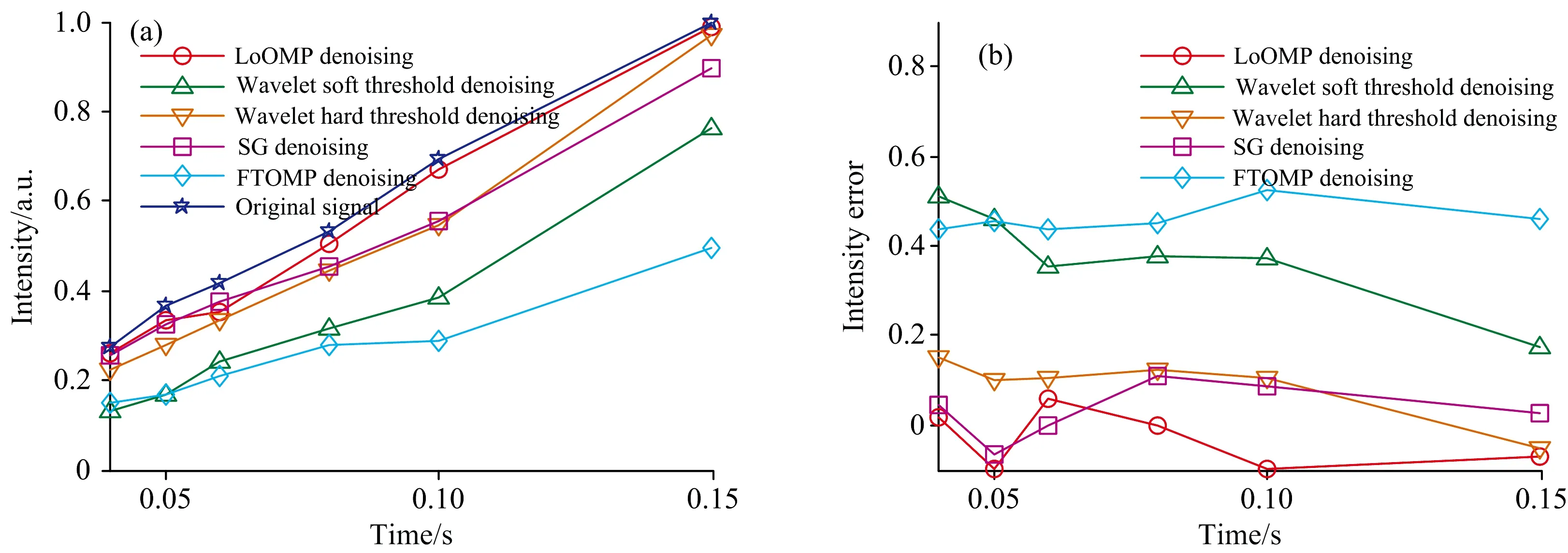
3 结果与讨论
4 结 论

