雷达测风组合的舰面稳态风向风速估计
张玉莹, 刘繁明, 卢志忠
(哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001)
舰面空气流场严重影响舰载机起飞降落安全,因此准确的舰面风场实测信息是海上舰船军事活动及军事作战的重要依据[1-2]。气流场通常随空间和时间不断变化,实际用户通常关注的是舰面稳态风速风向参数,定义为未被舰面结构物扰动的自由来流在空间和时间上的平均值,被直接用于舰载机起降时迎风角度的调整,测量准确度要求很高,对舰载机起降安全至关重要[3]。通常舰面桅杆处布置有2个或多个风速风向传感器,传统的测风方法简单选取各传感器中实测风速最大的传感器测量值输出[4],这种方法的应用前提是桅杆传感器布置区域的流场符合自由来流假设,不受舰面结构物的扰动。
然而由于舰船特别是军用舰船在桅杆处布置了越来越多的外部设备,上述假设已经越来越难以保证,导致实际输出的风向风速参数存在较大误差,已不能满足舰载机起降对测量精度的要求[5-6]。
直接利用桅杆处布置的风速风向传感器测量真风属于站点式现场测量类型,可实时、快速监测随时间变化的观测点处海面风场信息,相对而言置信度高[7]。Yelland等[8]应用流体力学(computational fluid dynamic,CFD)模型模拟船舶的气流流动情况,风速仪分别设立在良好暴露位置与非良好暴露位置对风速进行预测,但由于船舶本身会引起气流畸变,风速仪测量结果会产生10%的风速误差。Reinsvold等[9]研究了船舶运动对风场参数测量的影响,指出船舶横纵摇运动造成桅杆高处的风速计产生了很大的动态风畸变,并分析了船舶横纵摇、上层建筑对风速计的影响;针对舰船甲板气流场受舰面结构物遮挡的影响,郜冶等[4]以CFD计算软件为工具,对不同风速(工况)下传感器周边气流场的畸变情况进行了仿真,结果表明传感器当前安装位置向桅杆外平移后,将有利于降低风向、风速值的测量误差;船舶本身周围气流场易受船舶横纵摇的影响,针对这一问题,胡桐等[10]应用数值模拟计算的方法分析了舰船周围气流场的分布情况,并且应用实船实验数据对数值模拟计算得到的结果进行了验证。由于测风传感器安装在舰船桅杆时,不可避免受到周围结构物的遮挡,致使舰船遭遇的自由来流被破坏且无明显的规律,因此无法直接获得真实的风速风向信息[11]。
航海雷达也能用于反演距离本船1 km附近海面的平均风速风向信息,由于其独有的测量区域不存在结构物扰动、更接近自由来流的优势,已成为海面风场信息获取研究的热点[12-13],其中基于海面风场成像特征的算法被广泛研究,包括局部梯度法、自适应缩减法和能量谱法等[14]。Dankert等[15]提出局部梯度法提取海面风向信息;Wang等[16]提出自适应缩减算子提取海面风向,利用自适应局部梯度计算局部风向;Wang等[17]提出基于能量谱的海面风向提取技术,风向反演精度较其他算法精度有所提升。但因原理所限航海雷达测量手段仍存在误差较大的缺陷[18]。
文献[4]中利用CFD模型分析了不同风速(工况)下风传感器布放区域周围气流场的畸变特性,研究表明现有测风传感器布置条件下测风误差较大,但未能给出有效提高风速风向估计精度的方法。为了满足用户对精度提高的强烈需求,本文在文献[4]基础上开展了进一步研究,提出了一种四传感器布置方案,进而提出了基于雷达测风参数组合的四传感器加权融合舰面稳态风速风向估计算法(RFSF),在四传感器加权融合算法基础上,加入航海雷达图像反演所获得的风向参数作为先验条件,能够利用舰面桅杆处风速风向仪的实测值进行舰面稳态风向风速估计技术研究,有效降低了风场测量误差。
1 风传感器布置位置流场分析
便于对舰面风场的研究,本文将使用CFD数值模拟计算软件对舰面稳态风场进行相应的数值模拟。采用文献[4]中的方法验证传感器不同布置位置对风场参数的影响,根据文献[4]中在实船模型上的风传感器布放位置可知,现有风传感器布放位置的坐标为(0.0 m,3.68 m,13.23 m)和(0.0 m,-3.68 m,13.23 m),分别记为左舷监测点、右舷监测点,如图1所示。
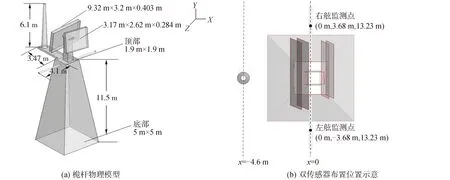
图1 双传感器现有布置位置Fig.1 The current location of two anemometers
应用CFD计算软件对舰面稳态风场进行数值模拟,由于风传感器安装位置向外移动有助于减小测量误差,当风传感器布放位置向前移动到天线位置处时,能够明显降低风速值的测量误差且风向值的测量误差不会显著提高,故改变舰船上风传感器的布置位置,并对风传感器附近的流场进行分析。由于风传感器在实船上的安装高度为13.23 m,用X、Y轴坐标值来表示风传感器的布放位置,忽略了Z轴坐标,以便于后文分析。在不改变风传感器安装高度的情况下,x的值分别取0和-4.6 m时,y的值分别取±3、±4、±5、±6、±7和±8 m(详见文献[4]),当风速为12 m/s时,风传感器在左、右监测点距桅杆不同距离处的气流场受湍流效应影响后的风向绝对误差、风速相对误差对比后可知,距离桅杆8 m处(x=0,-4.6 m)监测点的传感器所测风向绝对误差、风速相对误差最小。
本文对所测风场数据进行了进一步分析,结果表明左右舷监测点处所测得的风场与无穷远处真风场存在相当大的差异。由于双传感器传统算法目前仍存在较大的缺陷,风传感器现有布放位置受湍流效应的影响较为明显,使得双传感器现有的布放位置不能满足用户对风场参数估计精度的要求,风传感器即使被安装在舰船暴露良好的位置上,也有相当大的可能产生一个高达10%的风速误差[19]。针对双传感器布置方案的一些缺陷,通过分析文献[4],优选了分布在距桅杆中心8 m的位置处,在桅杆附近布放了4个相同规格的风传感器。其中,x=0,x=-4.6 m的横桁上各有2个风传感器,它们的布置位置分别为①和②、③和④,如图2所示,将多传感器所测风场信息进行融合来提高风场信息的精度。
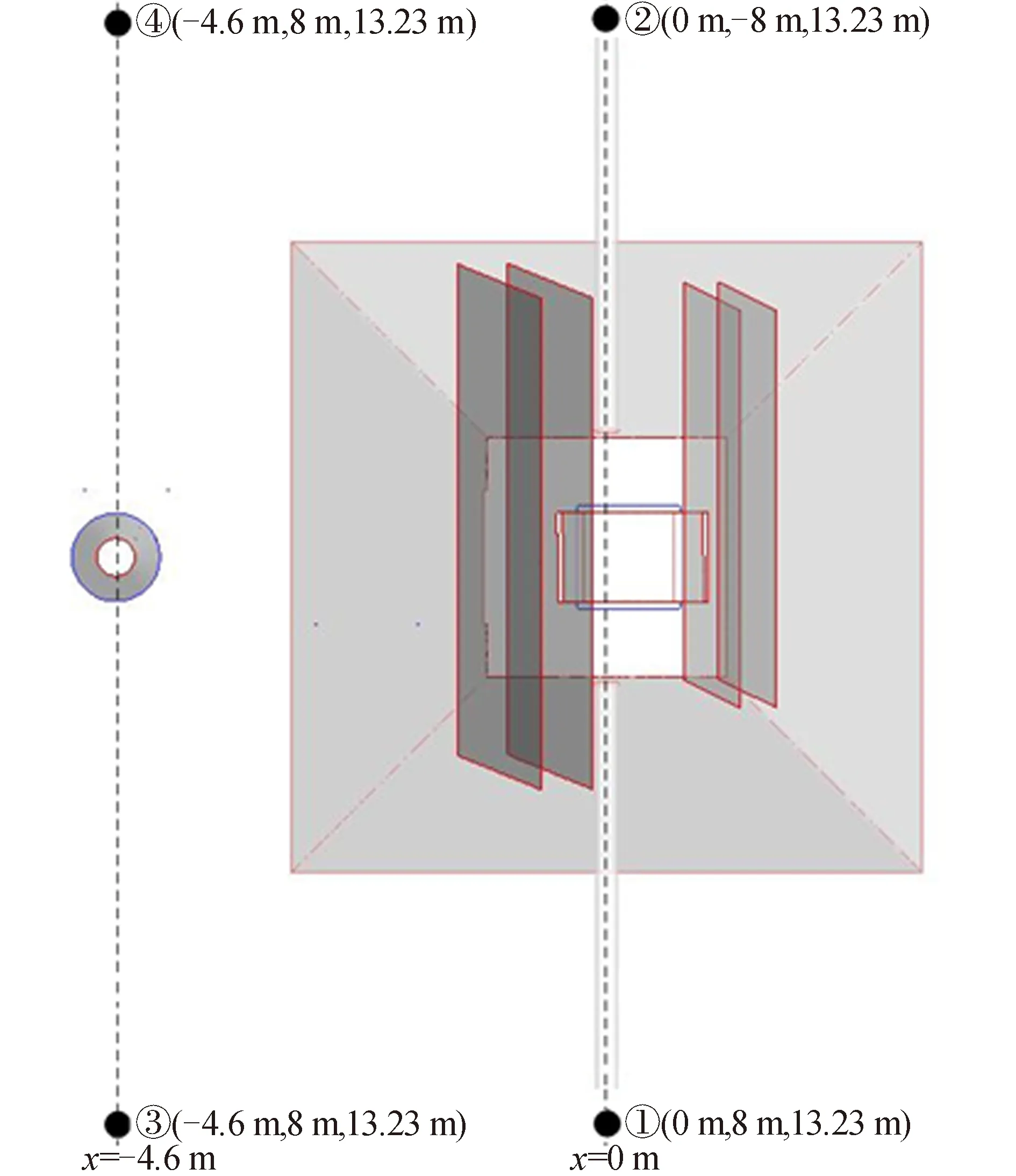
图2 四传感器布置位置示意Fig.2 Diagram of four anemometers layout
2 数据与方法
为了研究不同来风条件下舰面测风点的风向、风速畸变规律,本文使用CFD对舰船的表面风场进行数值模拟。在仿真过程中,首先选取x=0位置,并从横桁的+3 m和-3 m处向外扩散,以1 m为间隔每侧各选取6个测风点,故x=0处的测风点共计12个。此外,在x=-4.6 m位置处新增了以相同方式选点的横桁,这样一共选取了24个测风点。自由来流风场仿真初试条件方面,将真风速从3~15 m/s分为工况A、B、C、D、E这5种工况,每次递增3 m/s;对于每种工况,各均匀取72个风向角(从0°风开始每5°风递增直到360°)作为输入真风向。因此仿真数据中,每个测风点的数据为360组(每组数据包含一对风向风速值),24个测风点共计8 640组舰面稳态风场输入条件下的风场仿真数据,作为本文研究舰面稳态风向、风速估计技术的基础数据。
对CFD数值模拟仿真结果进行研究后发现,舰船上方无穷远处自由来流真风场与各拟布设传感器测风点观测值之间的偏差关系复杂,无法找到简单的函数关系式,表达自由来流与各观测值之间的关系模型。因此,本文探讨了应用非线性寻优方法解决上述问题,通过仿真模型得到传感器不同测风点的数据值,输入至非线性寻优模型中不断训练,进而估计出与无穷远处自由来流真风场误差最小的非线性关系式,实现最优估计。另外,多传感器可以从不同的位置、方向上获取更多方位、级别、层次的综合信息,因此能够反映更加丰富的差异性信息,故本文选取了多传感器数据融合的方法。
3 雷达测风组合四传感器加权融合算法
目前,多传感器数据融合算法中最常用的为最优加权算法,通过权值乘以各个传感器的测量值来估计测量参数的最优值[20]。4个相同规格的风传感器应用加权融合算法有其独特的优势,一方面,当多传感器系统中部分传感器发生故障时,可保证该系统仍然可以正常工作;另一方面,多传感器系统加强了对周围环境的描述能力,能够获得更加全面、准确的环境信息[21]。传感器测风的传统算法,其效果主要依赖测风位置是否受到船体上层结构物的遮挡效应,即取决于测风位置风向角的角度[22]。由于目前航海雷达反演风向的技术较为成熟,所得风向精度更高,故将雷达所测得的风向作为先验条件,在该风向角度下,对该风向角度范围约束下的传感器信息进行校验,进而进行风速风向估计。
3.1 航海雷达反演风向
随着海洋遥感技术的发展,使得利用雷达反演海表面参数成为可能,越来越多的人对航海雷达反演风向技术进行了研究,并取得了比较满意的结果[23-24]。采用文献[17]中基于能量谱海面风向反演算法获取精度高的风向,步骤为:
1)对实测雷达图像序列应用3×3模板的2-D非线性平滑中值滤波,抑制同频对海面风场研究的影响:

式中:g(s,t)为雷达图像像元点在极坐标位置(s,t)的图像回波强度值;f′(r,θ)为滤波后图像在极坐标位置(r,θ)的灰度值;N(r,θ)为中心点在(r,θ)处的像元点;(s,t)取以(r,θ)为中心的8个点。
2)将极坐标图像归一化,应用雷达图像序列建立全局低通滤波器,滤除海浪等高频信号,仅保留静态或准静态频率特征信号,主要为风场导致的风条纹信号;接着,将二维极坐标图像对应区域的极坐标应用最近点插值为笛卡尔坐标,将值赋予到已建立的笛卡尔坐标下。
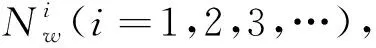
3.2 算法实现
将4个传感器所在位置(①、②、③、④)获取的数据作为基础数据,设每个风传感器之间不存在相互干扰,并且每个风传感器的测量值为真实值的无偏估计。因此,设各个风传感器X、Y轴的风速分量为Xxi、Xyi,其中i=1,2,…,n,n为传感器个数。ωxi、ωyi代表第i个传感器X、Y轴风速分量的权重值。每个传感器对应的权值计算如下(以计算X轴分量权值为例,Y轴分量权值计算过程相同):
(1)

(2)
估计值与各个风传感器的Xxi均视为X轴风速分量Xx的无偏估计,因此式(2)两侧得到的期望值相等,那么,传感器的权重系数之和为1:
(3)
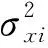
(4)
(5)
对上式的变量ωxi与λ分别进行求导,使导数为0,求出估计值方差的极小值:
(6)
权重系数的求解:
(7)
则传感器的估计值为:
(8)
式(8)中通过测量数据与参考数据计算得到各个风传感器的测量方差与权重系数。
将自由来流真风速vref与每个传感器布置位置风速vsensor沿X轴、Y轴进行正交分解,对0°~360°的风向范围以每5°为步长逐一进行分组。获取4个传感器的权值后,引入2.1节中导航雷达图像反演海面风向的测量数据θradar对传感器测量数据进行风向角度范围约束,由于应用EMS风向反演算法所获得风向标准差σ为8.29°,故可假设雷达测得的风向存在±20°(<3σ)的偏差,因此在雷达测得的风向约束角度θradar±20°范围内,将风向数据每5°分为一组,并对该风向角度范围内的所有风速的数据应用多传感器的最优加权融合算法,那么,传感器对应的权值分布为:
i=1,2,…,n,0°≤θradar≤360°
(9)
式中:i代表传感器的序号;n为传感器的个数(n=4);f(θradar)j代表查找得到的j组传感器对应权值,j为根据雷达测量风向分组序号,j=1,2,…,9。wxij、wyij为第j组第i个传感器的在雷达测量角度θradar下的X、Y轴分量的最优加权权值。
得到每个传感器对应的不同权值,估计每组角度范围下风速风向估计值:
(10)
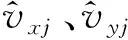
(11)
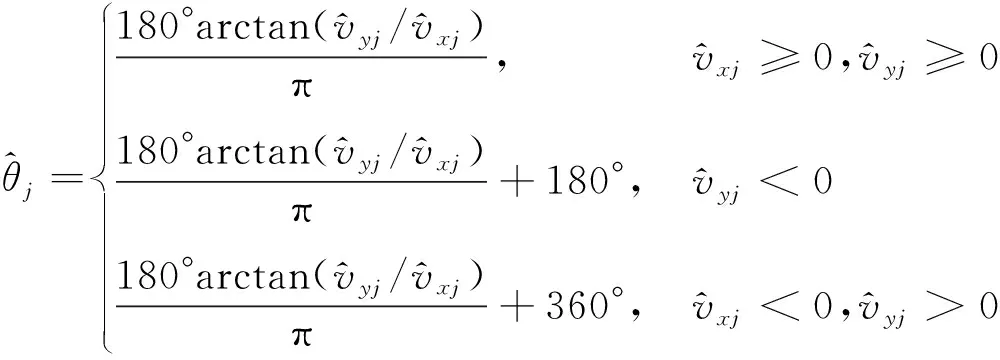
(12)
式中j=1,2,…,9。
引入代价函数,在θradar±20°范围内,取其中代价函数最小的那一组风速作为输出:
(13)
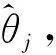
4 验证与分析
在真实环境中,远处吹来的自由来流势必会随着时间、空间的变化产生不可预知的随机变化,而本文研究舰面稳态风场时进行的CFD数值模拟仿真假设了无穷远处的风场在时间、空间上是均匀的。由于风传感器实测数据获取困难,且是否符合上述仿真设定的时间空间均匀性假设,以及偏离这种假设的程度均未知,因此本文应用CFD数值模拟计算的风场数据作为验证数据进行了算法性能初步分析,其局限性在于仅评估了符合时空均匀仿真假设理想条件下的算法性能。
根据CFD数值模拟仿真数据,对雷达测风组合四传感器融合算法(RFSF)分别从风速估算与风向估计两方面进行了验证评估,并与四传感器加权融合算法[25](FSF)的计算结果,分别分析了风速与风向的误差,其中风向使用了绝对误差MAE=|θm-θr|、风速使用了相对误差MRE=|(vm-vr)/vm|。
4.1 理想仿真条件下算法性能分析
图3为5种工况下(工况A-E的标准风速分别为3、6、9、12、15 m/s)FSF与雷达测风组合RFSF的性能分析对比图(理想仿真条件下)。
图3(a)为理想条件下的FSF风速相对误差,从图中可以看出风向角度范围为0°~180°,整体误差较高,风速相对估算误差分布在5%~15%的范围内。图3(b)为理想条件下RFSF的风速相对误差,大部分的风速相对误差值分布在8%以下的区域,只有极少数部分的点超过了8%。图3(c)为理想条件下的FSF风向绝对误差图,观察到整个图中风向绝对误差在5°以上的风向角度占很大比重,只有当风向角度为70°到110°范围内的风向绝对误差较低。图3(d)为理想条件下RFSF风向绝对误差,其中风向绝对误差主要分布在0°~5°内,大部分在5°以下,只有两侧与中间部分的风向绝对误差较大,但风向绝对误差最大值只达到7°。
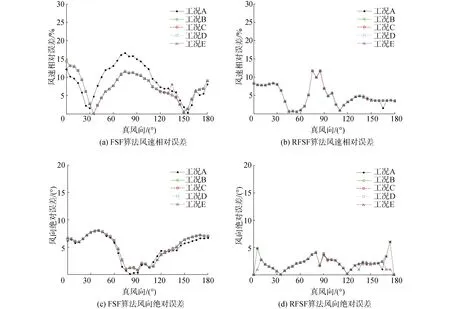
图3 理想条件下2种算法效果对比Fig.3 Comparison diagram of the two algorithms under ideal conditions
4.2 考虑噪声情况下算法性能分析
图4为加入传感器噪声情况下四传感器融合算法与加入传感器噪声情况下雷达测风组合四传感器融合算法的效果对比图。
图4(a)为传感器噪声条件下FSF风速相对误差,其中,风速相对误差主要分布在0%~18%内,位于10%左右的值较为密集。图4(b)为传感器噪声条件下RFSF的风速相对误差,其分布范围主要在0%~13%,且风速的相对误差值集中在8%以下。图4(c)为传感器噪声条件下FSF风向绝对误差,其分布范围集中在5°以上,在0°~5°分布的值只占少数。图4(d)为传感器噪声条件下RFSF风向绝对误差,其分布情况整体在0°~9°之内,且风向绝对误差在5°之下的值占绝大部分。通过图4可以看出,在风速较大工况下的风速相对误差与风向绝对误差明显优于风速较小的工况。
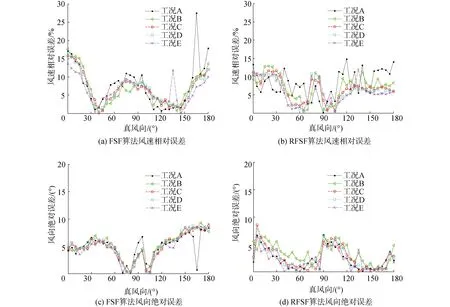
图4 加入传感器噪声情况下2种算法效果对比Fig.4 Comparison diagram of the two algorithms under anemometer noise
表1为理想情况下与传感器噪声下FSF与RFSF误差对比,从表中可以看出,理想情况下RFSF估计算法的风速相对误差则整体提升了2.14%,但风向误差均值相较于FSF的误差均值降低了2.54°;传感器噪声下RFSF的风速相对误差值比传统的方法精确度提升了0.13%,且RFSF的风向绝对误差较FSF精确了2.37°。
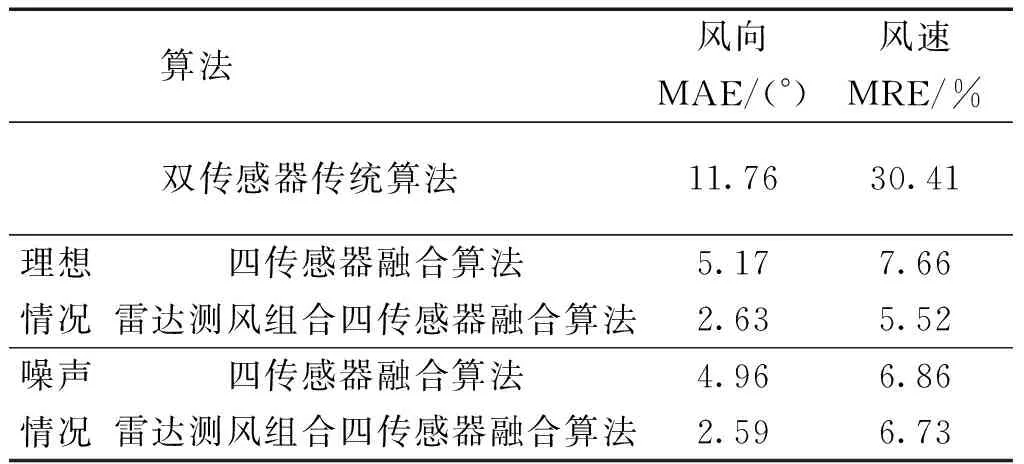
表1 不同情况下2种算法误差对比
5 结论
1)提出了将原有传感器位置向外移动并加入了2个同规格不同位置的传感器;
2)提出将不同位置的传感器数据进行数据融合的四传感器观测最优估计方案;
3)将传感器系统与遥感系统相结合,在四传感器数据融合风速风向估计方法中引入雷达反演风向参数,提出了基于雷达测风组合的四传感器融合风速风向估计方法。
4)本文旨在将航海雷达测得的风向、测风传感器测量的风向/风速等三者结合,在理想仿真条件下,对比四传感器融合算法,改进算法的风向误差均值降低了2.54°、风速相对误差提高了2.14%;加入传感器噪声条件下,风向绝对误差提高了2.37°、风速相对误差提升了0.13%。雷达测风组合的四传感器加权融合算法相对传统算法大大提高了校正后的风速、风向测量精度,相比四传感器加权融合算法其效果也更好。
仿真结果表明传感器噪声对于算法的风向误差影响不大,对风速误差影响稍大,可能是由于雷达测得风向的加入较好的校正了风向估计值。本文CFD仿真过程中未考虑船舶在海面上存在的横摇与纵摇情况,对于船舶在航行状态以及横摇、纵摇的情况,可做进一步研究。同时,通过仿真模型可得出传感器不同布放位置观测值的偏差规律,在此基础上结合舰船总体规定的传感器布放位置约束范围,可进一步综合评估传感器的最优布置方案,从而选取出传感器最优布放位置。

