小波分解和改进卷积神经网络相融合的水声目标识别方法

黄擎， 曾向阳

(西北工业大学 航海学院，陕西 西安 710072)

水声目标分类识别技术是水声探测领域的关键技术，也是水声信号处理中的重点和难点[1]。通常将水声目标识别过程分为特征提取和分类决策2个相对独立的部分。针对这2部分均已开展了大量的研究，提出的各种算法的有效性也得到了证明。但分步处理的方法未考虑提取的特征与分类器之间的“耦合”作用，因而构建的识别系统性能难以达到最优。

近年来，深度学习[2-3]在机器学习领域异军突起，与传统方法不同，深度学习只需要输入含有丰富目标特性的信息，通过逐层学习挖掘，从而可通过自动提取出最具有鉴别力的抽象信息进行识别。从系统连接的角度看，深度学习中的特征提取和模式识别是一个整体，避免了传统方法由于分步执行特征提取和模式识别导致的系统“耦合”作用，能进一步提升识别系统的性能。目前，最常见的深度学习算法-卷积神经网络(convolutional neural networks, CNN)已开始在水声信号处理[4]和水声图像处理[5-6]方面得到广泛地应用。CNN可通过结合局部感知区域、共享权重、空间或时间上的池化降采样3大特点来充分利用数据本身包含的局部性等特征在保证一定程度上的位移不变性[7]的基础上来优化网络结构，这使得CNN可用于水声目标识别。本文针对深度神经网络训练过程中会产生内部协方差偏移(internal covariate shift，ICS)以及随机梯度算法在局部极值附近的摆动幅度较大、优化速度较慢的问题，引入批量标准化层(batch normalization，BN)和自适应力矩估计(adaptive moment estimation，Adam)梯度优化算法对CNN进行改进。

CNN可直接输入信号的波形或频谱，考虑到小波分析在非平稳信号处理中的优势，本文将其与改进CNN算法融合，提出一种名为WAVEDEC_CNN的水声目标识别方法。该方法首先将原始信号用小波分解进行预处理(不同于传统的基于小波分解的小波去噪方法，本文提出的方法不对分解后的小波系数进行任何处理)；再输入改进的CNN对目标进行识别。在实验验证阶段，先将本文提出的方法与MFCC特征提取+SVM分类器方法进行对比；然后与无预处理的卷积神经网络(NO_CNN)、小波包分解预处理结合卷积神经网络(WPDEC_CNN)以及经验模态分解预处理结合卷积神经网络(EMD_CNN)的方法进行对比。

1 WAVEDEC_CNN识别方法

本文提出一种名为WAVEDEC_CNN的水声目标识别方法。该方法将小波分解和基于梯度优化和层批量归一化改进的CNN算法融合。

1.1 改进的卷积神经网络

与深度学习中的传统框架相比，卷积神经网络是局部连接并且权值共享，大大减小了网络参数，同时池化层下采样通过减少网络节点数，可进一步减小参数数量。这对于高维输入数据尤为重要。同时，CNN利用卷积层进行信号的增强，并利用池化层获得具有位移、时移或旋转不变的特征，最后通过全连接神经网络进行分类。从整体上看，卷积层和池化层的交替使用可以使模型具有良好的稳健特性。

与传统的CNN不同，本文提出的模型在卷积和池化层之间引入了批量标准化层。由于CNN 每层的输入都受到前面所有层参数的影响，网络参数的微小变化会随着网络的深化而放大，这使得训练变得复杂。为解决这一问题，本文采用自适应力矩估计对梯度进行优化。该方法易于实现，计算效率高，对内存的需求小，不受梯度的对角调整的影响，可用于数据和/或参数很大的问题。

1.1.1 参数优化方法

白化输入可以加快网络收敛速度，在此基础上Loffe[8]提出可以在网络任意隐层加入BN层来减小训练过程中的内部协方差偏移，从而防止梯度消失，同时，该模型允许使用更大的学习率，从而加快网络收敛速度。

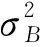
(1)

(2)

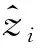
(3)

式中：yi为标准化后的输出，γ和β为与BN层高斯分布有关的可学习的超参数。参数更新：

(4)

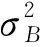
(5)

根据均值和方差的梯度可以获得反向传播过程中BN层输出结果的梯度：

(6)

BN层与高斯分布有关的超参数梯度：

(7)

由于识别过程中，无法直接获得测试样本的均值和方差。因此识别过程BN层使用训练过程中各批量的均值E[x]和方差Var[x]的无偏估计，参数设置为：

(8)

识别过程中高斯分布超参数设置为：

(9)

识别过程中测试样本更新公式为：

y=γ′·zi+β′

(10)

1.1.2 Adam梯度优化方法

Kingma[9]提出Adam梯度优化算法。该方法将动量法和均方根传播算法相结合，优化了随机梯度算法在局部极值附近的摆动幅度较大和优化速度较慢的问题。

Adam梯度下降过程中动量法和均方根传播算法中权重和偏差初始值均设为0。vdw和vdb表示动量法中权重和偏差一阶矩指数加权平均数，sdw和sdb表示均方根传播算法中权重和偏差二阶矩指数加权平均数。初始化方法为：

(11)

Adam梯度下降过程动量法vdw和vdb参数更新为：

(12)

式中β1表示一阶矩累加的指数。

Adam梯度下降过程均方根传播算法sdw和sdb参数更新公式为：

(13)

式中β2表示二阶矩累加的指数。

Adam算法权重W和b更新公式为：

(14)

式中α表示学习率。

1.2 小波分解和改进神经卷积神经网络融合方法

CNN已开始在水声目标识别方面得到广泛地应用，考虑到小波分析在非平稳信号处理中的优势，本文将其与改进的CNN算法融合，提出了一种名为WAVEDEC_CNN的水声目标识别方法。

小波分析与加固定窗的短时傅里叶分析方法不同，可以用不同形状的窗函数(小波基函数)分析处理信号，从而实现低频处获取较高的频率分辨力、高频处获取较高的时间分辨力。

小波基函数定义为：

(15)

式中φ(t)为基小波或者母小波函数，经过尺度因子a和平移因子b变换后的φa,b(t)统称为小波。

对于离散情况：

φj,k(t)=2-j/2φ(2-j/t-k)j,k∈Z

(16)

采用离散小波变换(DWT)表示分解原始时域波形信号，得到原始信号的近似(低频)成分和细节(高频)成分。小波分解表示将原始信号经过DWT变换后的低频成分再进行DWT变换，循环次数由分解层数决定。

多层小波分解预处理后，将每层小波系数拼接作为CNN网络的输入。由此得到的WAVEDEC_CNN方法原理图如图1所示。

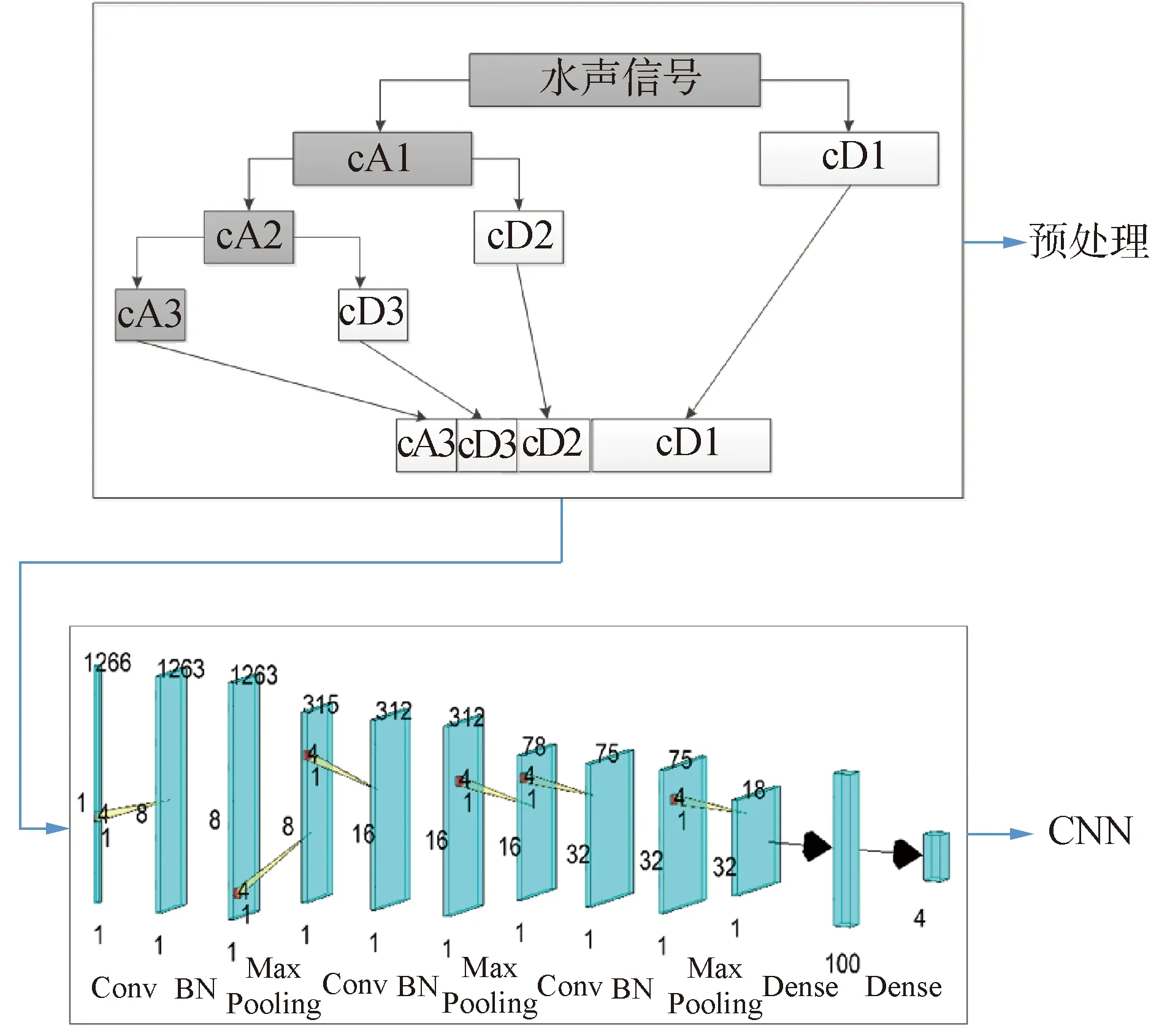
图1 WAVEDEC_CNN原理Fig.1 Schematic diagram of the WAVEDEC_CNN

图1上半部分表示以3层小波分解为例，对时域信号进行预处理。其中cA1、cA2和cA3表示的是每层分解的低频近似信息；cD1、cD2和cD3表示的是每层分解的高频细节信息。下半部分表示的是卷积神经网络模型，每层数字表示该层尺寸，相邻层连接线的数字表示滤波器尺寸。

pre_wavedec=[cA3,cD3,cD2,cD1]

(17)

小波分解重构误差由下面公式给出：

(18)

式中：norm2表示求向量的2范数。datareci表示每层小波系数重构的时域信号。

以3层小波分解预处理为例，原始信号、小波分解重构信号和本文使用卷积神经网络输入如图2所示。

图2从上至下分别表示原始信号、重构信号和由式(17)得到的卷积神经网络输入样本。原始信号和重构信号经式(18)计算的重构误差为1.7×10-11。说明小波分解没有丢失信息。从最下面的图可以看出能量主要集中在该样本的前部分。这是因为原始信号是某段民船辐射噪声信号，民船辐射噪声信号主要集中在低频部分，而由式(17)可以看出该样本的前部分主要表示的是原始信号的低频信息cA3。

图3为原始信号3层小波分解的cA3、cD1、cD2和cD3系数图。

图3分别表示第3层分解的低频信息和逐层分解的高频信息。其中低频信息整体幅度最大，这是因为原始信号能量主要集中在低频部分。这与图2中样本结果一致。

结合图2和图3，小波分解预处理不仅不会丢失信息，同时将原始信号自动按频带划分，与原始信号比较，更能凸显信号特点。这对目标识别是有利的。

图2 信号小波分解预处理结果Fig.2 Result diagram of the signal with the wavelet decomposition preprocessing

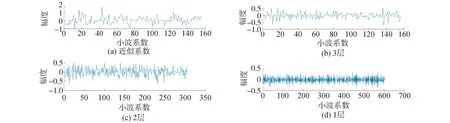
图3 3层小波分解系数Fig.3 Coefficient diagram of 3-layer wavelet decomposition

最后在改进的卷积神经网络训练阶段，联合优化交叉熵损失函数J：

(19)

式中：y(i)表示第i类真实标签；xwdec(i)表示经过离散小波变换预处理的输入样本；fnet(·)表示本文改进的卷积神经网络。

2 实测数据实验

本文实验数据集来自课题组在丹江口水库湖试获取的数据。数据包含4个水面目标：铁皮船1、快艇2、快艇3和快艇4。湖底布放2个8元线列阵，采样频率为48 kHz。每艘船绕行2个阵列3圈，每圈截取21段(每段10 s)数据，共4×3×21×10=2 520 s。每圈取14段作为训练集，剩余7段作为测试集。将每段信号按0.1 s分帧，每帧为1个样本，因此，训练集样本总数为16 800，测试集样本总数为8 400。

超参数设置：学习率0.01；每次实验训练30轮，每轮采用批量梯度下降法求梯度，每个批量为100。重复实验50次，每次实验都随机初始化权重。梯度优化算法为adam算法，一阶矩估计的指数衰减率为0.9；二阶矩估计的指数衰减率为0.999。L2正则项为10-4。CNN隐藏层设置3个卷积层、池化层和一个全连接层。卷积层滤波器为1×4，步长为1。滤波器数目分别为16,32和64。池化层为1×4，采用最大池化，步长为4。

图4～7为实验结果。其中图4表示的是重复实验50次，每次的识别结果。图5表示从湖试数据截取的84段声音文件的识别结果。图6表示每艘船的识别结果。图7表示的是本文所用的各种深度学习方法识别结果的混淆矩阵结果图。表1是实验结果和运行时间，包括从湖试截取的声音文件构建样本集用的时间和用卷积神经网络进行训练和识别的时间。

图4 识别结果对比Fig.4 Comparison diagram of the recognition results

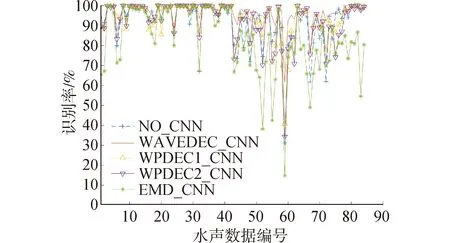
图5 不同水声数据识别结果对比Fig.5 Comparison diagram of different underwater acoustic

图6 不同船识别结果对比Fig.6 Comparison diagram of different ships recognition results

结合图4和表1可以看出，本文提出的WAVEDEC_CNN方法识别效果最优。识别率较NO_CNN、WPDEC1_CNN和EMD_CNN等方法分别提升了4.41%、3.23%和12.81%。其中WPDEC1_CNN方法和WPDEC2_CNN分别执行了10层和4层小波包分解。虽然小波分解预处理耗费了一定时间，但是总的运行时间反而最短。

与WAVEDEC_CNN对比，虽然WPDEC_CNN的频带划分更为精细，但是相同的分解层数条件下，执行DWT的次数远高于WAVEDEC_CNN。以分解层数N=10为例，WAVEDEC_CNN执行了10次DWT运算，WPDEC1_CNN执行了210-1=1 023次DWT运算。因此构建样本集时WPDEC1_CNN方法花费大量时间，从表1可得约为WAVEDEC_CNN方法的118.5倍。同时WPDEC1_CNN方法表示的信号维度较大，用CNN进行训练消耗更多时间，约为WAVEDEC_CNN方法的6.99倍，大约需要9.46 h。虽然WPDEC_CNN方法和WAVEDEC_CNN方法重构误差都是小量级的(以某一样本为例，重构误差量级为10-12)，但是预处理后数据的维度大大提升，信息过于分散，识别率反而下降3.23%。因此，设置另外一组对比实验，设置N=4，记为WPDEC2_CNN。在此分解层数下，WPDEC2_CNN方法执行DWT运算为15次，构建样本集时间仅为WAVEDEC_CNN方法的3.33倍，约为原来的2.8%。实验结果表明其识别率较N=10时下降了0.75%，比WAVEDEC_CNN方法下降了3.98%。这说明较低的分解层数，虽然可以大幅度降低WPDEC_CNN的运行时间，甚至和WAVEDEC_CNN方法相媲美，但是分解层数较低时，其对低频的划分反而不如WAVEDEC_CNN方法精细，识别率低于本文提出的方法。NO_CNN运行时间也较短，但是识别率相比WPDEC_CNN方法下降4.41%。

从实验结果可以看出，EMD_CNN方法识别效果最差。虽然经验模态分解后的残余信号分量较少，重构误差也较低，但是EMD_CNN方法没有明确的基函数，分解过程存在模态混叠效应[10]。表现为对于不同的样本，其每阶模态表示的信号瞬时频率的频带范围可能不一样，导致识别结果最差。

图7表示的是每种方法某次实验结果的混淆矩阵。因为表1深度学习识别结果是50次实验的平均值而且方差均较小，所以这些混淆矩阵也是具有代表性的。混淆矩阵右下角结果表示的是准确率。混淆矩阵中最下面1行前4列结果分别表示每类目标的召回率，最右边1列前4行中数字表示每类目标的精确率。混淆矩阵行表示的是预测为行数对应类别的数目。每一列表示的是当前预测结果真实类标为对应列数。对角线上前4个结果分别表示每类预测正确的样本数。

图7(a)到(c)可以看出，WPDEC1_CNN和WPDEC2_CNN方法相比WAVEDEC_CNN方法，在第3类和第4类目标上存在明显的错分问题，其精确率均较低。对于第3类，WPDEC1_CNN和WPDEC2_CNN方法分别把80和172个样本错分为第4类，WAVEDEC_CNN方法仅为27个。对于第4类，WPDEC1_CNN和WPDEC2_CNN方法分别把127和112个样本错分为第3类，WAVEDEC_CNN方法仅为18个。说明本文提出的WPDEC1_CNN方法增加了第3类和第4类之间的区分度。

图7(d)可以看出，对于EMD_CNN方法，由于存在模态混叠效应，其各类精确率均最低。特别是第3类和第4类，存在严重的错分问题。对于第3类，将323个样本错分为第4类，占第3类样本数323/2 100=15.3%。对于第4类，将396个样本错分为第3类，占第4类样本数396/2 100=18.9%。

从图6可以看出，除了EMD_CNN方法外，其他方法对于船1不同圈的识别效果都较好，分别为95.65%、96.60%、95.49%和95.75%，本文提出的框架效果最好，对比其他方法识别率至少提升0.95%。这是因为船1为铁皮船，船2到船4为不同型号的快艇，铁皮船和快艇目标特性差异较大。从图5可以看出，对于第59段声音样本几种方法识别率差别较大，因此，对其专门进行分析。图8(a)为第59段声音文件，它来自船3第3圈。各方法识别结果分别为31.14%、61.74%、40.70%、34.32%。图8(b)为第60段声音文件，同样来自船3第3圈。各方法识别结果分别为80.22%、92.42%、67.76%、78.42%。每段声音文件长度为10 s。

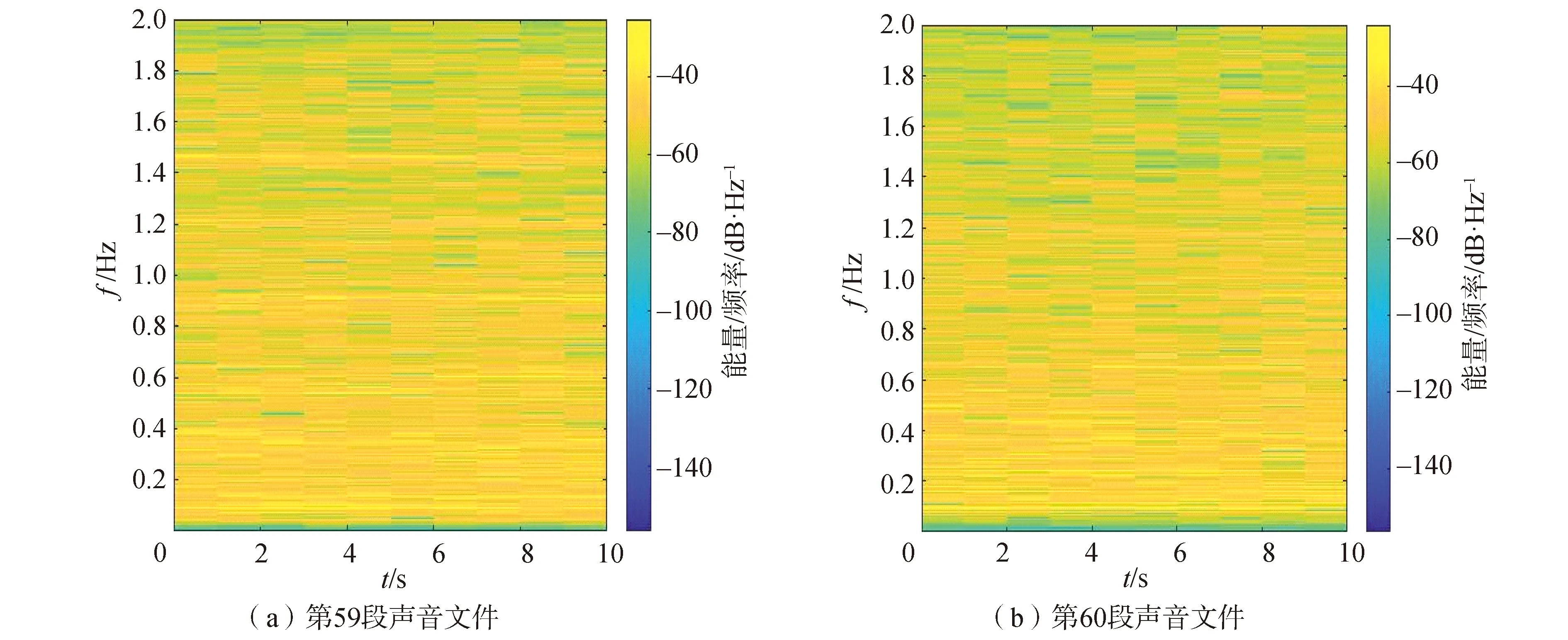
图8 第59段和第60段声音文件STFT图Fig.8 STFT diagram of the 59th segment and 60th segment of underwater data

对比图8(a)和图8(b)可以看出，第59段和60段声音在1 000 Hz以内时频分布基本一致。但是第59段声音文件在1.465 kHz处存在干扰，大约持续7 s。这可能是其他方法在第59段声音处识别效果较差的原因。这也说明本文提出的WAVEDEC_CNN抗干扰能力较强。

3 结论

1)与NO_CNN、WPDEC_CNN和EMD_CNN相比，本文提出的识别框架的识别率有明显的提升。

2)WPDEC_CNN方法虽然重构误差较低，但预处理和网络训练需要花费大量时间。EMD_CNN由于存在模态混叠反而效果最差。但是这些方法识别性能都优于传统的识别方法。

因为不同小波基构造的小波滤波器性能可能不一样，同时较高的分解层数，可以获得较为精细的频带划分，能否更好的区分干扰和目标，因此下一步将更加深入的研究不同小波基和不同的分解层数对识别结果的影响。