基于时间反演的上行NOMA系统能效优化算法

陈善学, 吴生金, 谷博文

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065; 2. 移动通信教育部工程研究中心, 重庆 400065; 3. 移动通信技术重庆市重点实验室, 重庆 400065)

0 引 言

近年来,随着移动通信技术的飞速发展和移动终端数量指数增加,各类网络服务与应用不断涌现,移动设备的能量消耗和人们日益增长的速率需求的矛盾变得愈加明显。另一方面,考虑到无线通信用户大多处在复杂的环境中,其时变多径传播特性也会影响通信性能,因此如何权衡在复杂环境下系统传输速率和系统能耗的关系是一个亟待解决的关键问题。

为了解决上述问题,非正交多址接入(non-orthogonal multiple access,NOMA)技术和时间反演(time reversal,TR)技术应运而生。具体来说,NOMA是一种能够在同一资源块上为不同用户提供服务的多址接入技术,以解决当前频谱资源匮乏和移动终端大量接入的服务质量问题,从而为通信网络提供低能耗、高效率的服务。此外,TR技术可以充分利用多径环境的特性,为低复杂度高能效通信提供了巨大的潜力,TR是一种利用多径效应创造空时聚焦效果的信号处理技术,不仅能够极大地增强接收端的信号强度,且还能降低用户间干扰。因此,将TR引入到多径环境下的上行NOMA系统中具有重要意义。

与此同时在未来的无线通信系统中,高密度设备如物联网(internet of things,IOT)系统中巨大的能量消耗成为不可避免的问题,由于大多数终端设备的电池容量一直都是个待处理的问题,因此在设计通信系统时,需要考虑系统能效(energy efficiency,EE)的性能。此外,NOMA的海量连接能力,使其有能力成为改善物联网系统通信问题的有效解决方案。因此,针对NOMA系统的研究受到了学术界和科学界的广泛关注。文献[17-18]研究了NOMA系统中发送端的功率分配方案以及接收端的串行干扰消除(successive interference cancellation,SIC)检测算法。然而,用户端的信号处理能力有限,上行NOMA系统研究更加符合实际。如今,大部分文献研究是针对上行NOMA系统,但考虑能量效率的相对较少。

通过资源分配可以有效提高NOMA系统的资源利用率,合理配置网络中的无线资源。目前对上行NOMA资源分配问题的研究已取得一些有价值的成果,针对上行NOMA网络,文献[22-25]研究了NOMA系统的功率分配问题,文献[22]分析了在用户的服务质量和最大发射功率的约束下,最大化系统能效。针对单小区用户的公平性,文献[23]提出了资源分配方案,提升了用户速率,却忽略了系统能效问题。文献[24]研究了多用户多载波的最优功率分配因子和子载波分配问题,同时考虑系统的能效优化,但系统复杂度也将成倍的提升。文献[25]考虑了上行链路子信道排序问题和功率的分配问题,通过注水算法与几何规划技术解决了系统资源分配。上述文献均没有考虑现实中多径传播对系统的影响,为了更加贴切实际情况,本文考虑用户在丰富散射环境下的通信,并对系统能效问题进行建模及解决。

本文研究了基于TR技术的上行NOMA系统中资源分配算法,最大化系统能效,主要贡献如下。

为了解决在多径环境下NOMA系统能效较低问题。首先,在传统上行NOMA模型中加入了TR技术,建立了一个多簇多用户的TR-NOMA传输方案。其次,本方案考虑了每个用户的用户服务质量(quality of service,QoS)和最大发射功率作为约束,构建了系统能效的资源分配问题。由于所提的资源优化问题是一个非凸形式,不易获得解析解。利用Dinkelbach算法和连续凸逼近方法将所提问题转为可解的凸优化问题,并利用拉格朗日对偶原理求得系统最优解。最后,通过仿真分析验证了本文所提算法的正确性。

1 系统模型

本文考虑了基于TR的NOMA通信模型。如图1所示。系统为NOMA上行链路场景,将个用户分为个NOMA用户组,假设用户已完成分组,用户组之间不存在干扰。本文主要考虑了其中一个用户组,该用户组包含个用户(≥2),不失一般性,假设个用户在同一频谱上同时向基站发送信号,基站和用户端均配备单天线,基站到第个用户的信道表示为,信道之间相互独立。假设系统的信道状态信息在一个相干周期内保持不变,基站是获知完美的信道状态信息,即从信道探测阶段到信号再发送阶段信道状态信息保持不变。

图1 TR-NOMA系统模型Fig.1 TR-NOMA system mode

对于上行TR-NOMA,由于SIC位于基站侧,首先被解码的用户将会受到同一组中其他用户的干扰,而解码顺序较晚的用户,受到同组的干扰会相应减少。为了尽可能降低SIC的负面影响,通常处理方式是根据用户到基站的信道增益大小来决定译码的顺序,信道增益越高越早解码,理想情况下信道增益最低的用户在传输过程中无用户间干扰传输。假设用户组1中用户的信道增益由低到高排序||≤||≤…≤||。

本文模型考虑实际中多径效应对系统的影响。具体来说,假设个用户同时发送信号,用户和基站之间的信道增益为

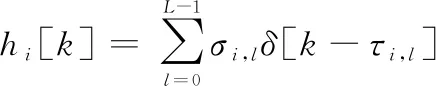
(1)

式中:表示场景中多径条数;,、,分别表示用户的发送端到接收端的第条多径的幅度与时延,且满足均值

E[[]]=0。

图1中,TR-NOMA的通信过程分为3步。

基站向用户发送探测信号,用户端接收并记录信号。

信号在利用TR镜(TR mirror,TRM)将探测信号进行时域反转得到[]。

正式通信阶段,TRM发射反转后的信号,信号在基站处聚焦,最后基站向用户发射功率控制信息。

在模型中加入TR后,信道增益[]变为[]*[],*为卷积,[]由[]经TR和归一化得到：

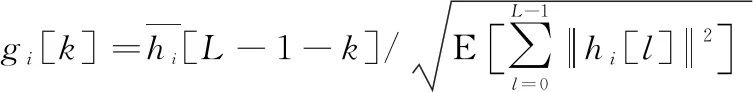
(2)

信号通过TRM后,信道增益为

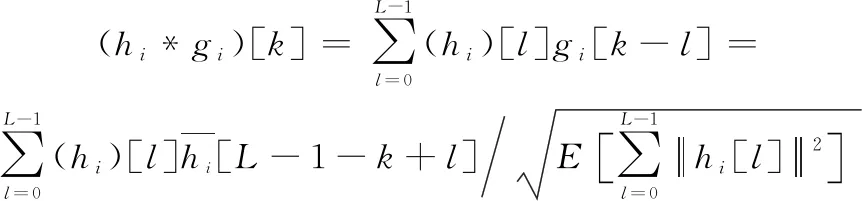
(3)

式中:∀,∈{0,1,…，2-2}。当取-1时,对应公式上产生自相关函数,存在最大功率中心峰值,即

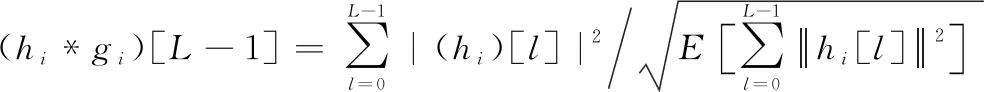
(4)

对于通过TRM后传输的信号,由文献[26]可知,信号的绝大部分功率会在中心抽头上聚焦,即第-1个抽头,所以本文考虑将第-1个抽头上的功率作为理想信号的功率。

通过上述的分析TR-NOMA系统中基站的接收信号表示为

(5)

式中:为第个用户向基站发送的功率;表示第个用户向基站发送的信号,且E[||]=1；为第个用户到基站的信道增益,为发送滤波器脉冲响应；表示均值为0、方差为的加性高斯白噪声(additive white Gaussian noise,AWGN)序列。

接收端第个用户的SINR可以表示为

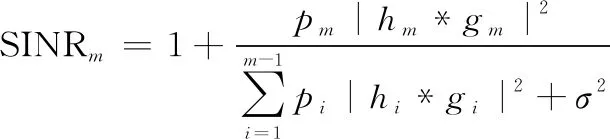
(6)

式中:为噪声功率,根据NOMA协议,第个用户的最大可达速率表示为

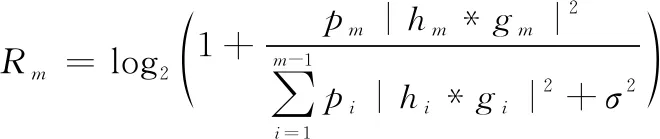
(7)

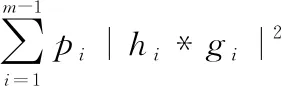
2 问题规划和算法设计

2.1 问题规划

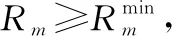
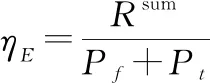
(8)

因此,所考虑的能效最大化优化问题可以表述为

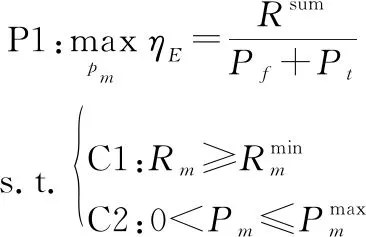
(9)

式中:约束条件C1和C2分别表示每个用户的最小速率门限和最大发射功率门限。

2.2 算法设计

根据问题P1,目标函数(9)为非线性分式规划问题,是非凸问题,处理起来较困难并且很难获取它的全局最优解。因此,利用Dinkelbach算法,分式规划问题可以改写为参数相减的形式,即转化为

s.tC1,C2

(10)

由于P2中传输速率中含有耦合变量,使得P2仍然是一个非凸问题,针对这个问题,本文使用了连续凸近似法将优化P2转化为凸优化问题,利用下界迭代得到最优解,具体分析如下：

log()+≤log(1+)

(11)

式中:和分别定义为

(12)

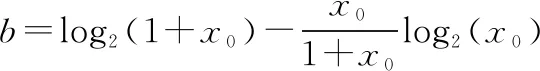
(13)

当=时,以上不等式等号成立。首先,定义

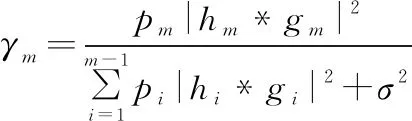
(14)

因此,数据速率可以近似为

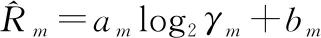
(15)

其中,

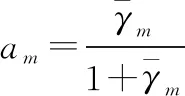
(16)

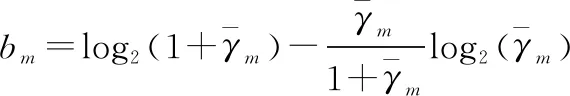
(17)

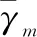
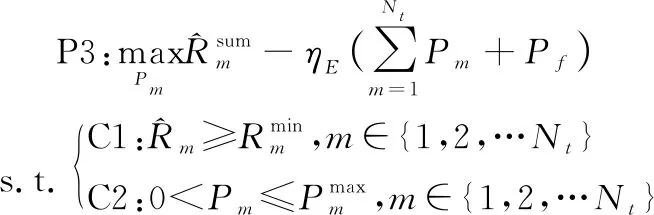
(18)

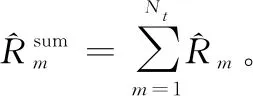
P3是一个确定的凸优化问题,有唯一的最优解,因此可以通过拉格朗日对偶法解决。基于优化问题3的拉格朗日函数可以写为

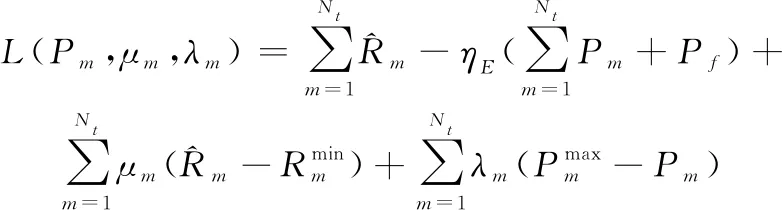
(19)

式中:≥0,≥0是优化问题P3的约束条件所对应的非负拉格朗日乘子。进一步将拉格朗日函数可以表示为

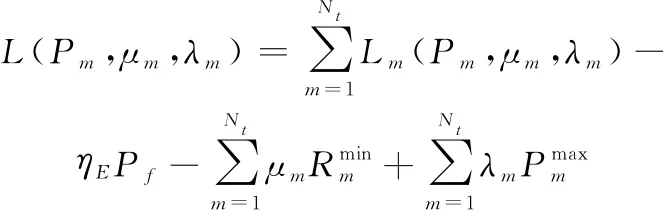
(20)

式中:

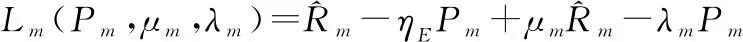
(21)

对于给定的能效,优化问题3的对偶问题,表示为

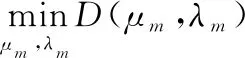
(22)

式中:对偶函数为

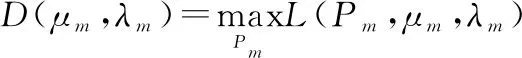
(23)

根据KKT条件,可以得到最优功率分配的解析解为

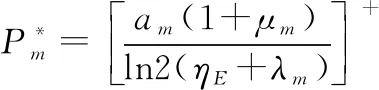
(24)

式中:[]=max(0,)。

使用次梯度法,拉格朗日乘子可以进一步更新为

(25)

(26)

式中:为迭代次数;Δ和Δ为相应的迭代步长。算法流程由算法1给出。

算法 1 基于迭代的联合功率分配优化算法初始化系统参数:Nt,hm,Pf,Rminm,Pmaxm,flag,σ2;定义算法的收敛精度ξ,以及最大迭代次数Tmax;初始化迭代次数t=0,初始化能效ηE=0;1 循环2 根据初始化系统能效ηE,求解目标问题式(18)3 输出相应的变量解Pm(t)4 如果|^Rm(t)-ηE(Pm(t)+Pf/Nt)|<ξ成立5 令flag=1,更新P*m=Pm(t),输出并返回6 否则令flag=0,并且t=t+1,7 更新能效为ηE=^Rm(t)Pm(t)+Pf/Nt8 结束9 循环直到flag=1或者t=Tmax10 输出最优变量P*m。

2.3 算法复杂度分析

本文在上行TR-NOMA系统模型下,提出了联合优化发射功率的能效最大化的资源分配算法。假设外层能量效率的最大迭代次数和内层拉格朗日迭代次数分别为、,则内层迭代更新计算复杂度和Dinkelbach外循环求解的最大计算复杂度分别为()、(),用户簇内共有个用户,系统用户一共分成了个簇,算法的总计算复杂度为()。通过选择合适的迭代步长,对偶算法可以很快取得收敛。

3 仿真结果与分析

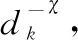
表1 仿真参数

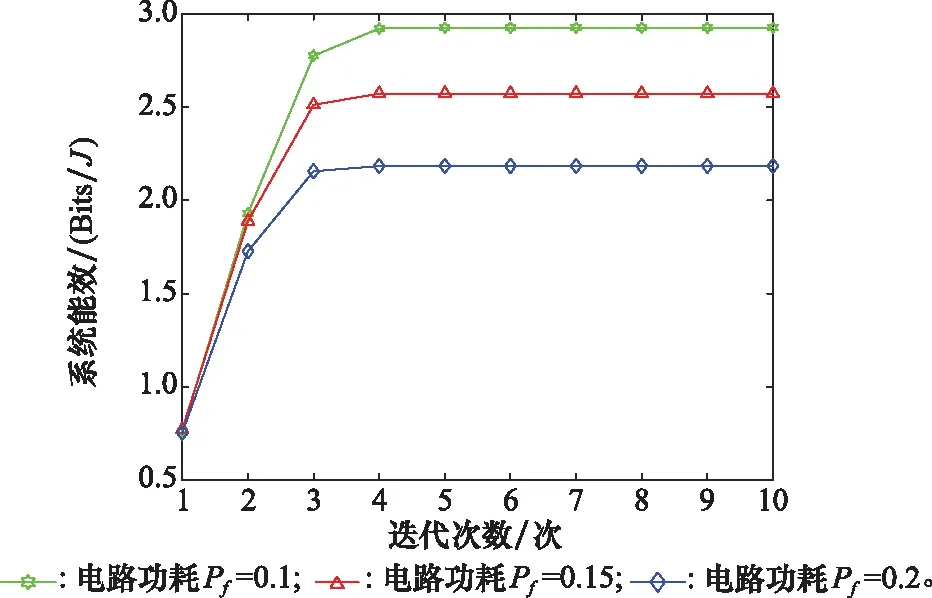
图2 系统能效在不同电路功耗下的收敛性能Fig.2 Convergence performance of system energy efficiency under different circuit power consumption

图2给出了系统中在不同电路功耗下的收敛性能。从图中可以看出,经过系统迭代次数的增加,系统能效逐渐增大直到收敛,有效证明本文所提算法正确性。假设其他参数不变,同时设置系统的电路功耗为0.1、0.15、0.2,随着系统的功耗增加,系统能效越低。其原因是最大发射功率在一定情况下,系统电路消耗功率越多,能量效率也就越低。

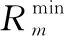
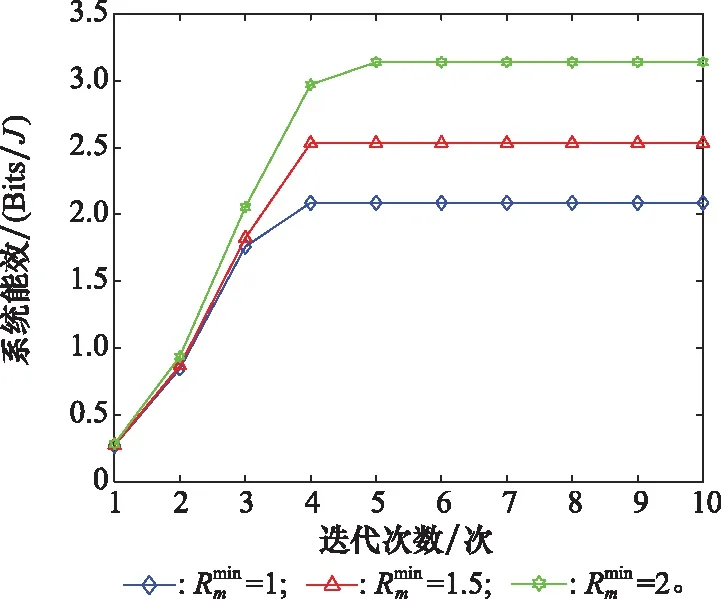
图3 能量效率在不同最小传输速率下收敛性能Fig.3 Energy efficiency convergence performance under different minimum transmission rates

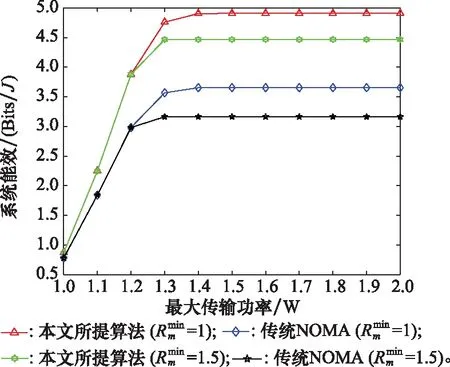
图4 最大传输功率和最小传输速率对能量效率的影响Fig.4 Influence of maximum transmission power and minimum transmission rate on energy efficiency

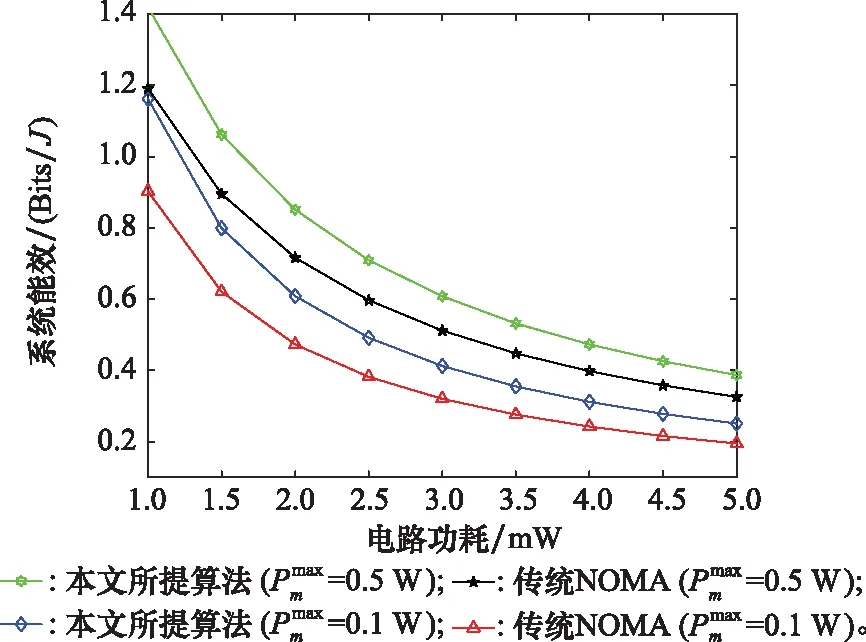
图5 电路功耗和最大传输功率对能量效率的影响Fig.5 Influence of circuit power consumption and maximum transmission power on energy efficiency

4 结 论

本文提出了基于时间反演的上行NOMA系统能效优化算法。具体来讲,考虑了簇内用户的QoS约束,以及用户的最大发射功率约束,通过利用TR技术独特的空时聚焦性能与功率分配策略来使得系统能效最大。由于所提问题为二元分式非凸问题难以获取闭式解,所以,利用了Dinkelbach法和连续凸逼近法将原问题转化为等价的凸优化问题。并根据拉格朗日对偶原理求得闭式解。仿真结果表明,本文所提能效优化算法具有较好的收敛性和能效。