考虑随机冲击影响的多部件系统视情维修与备件库存联合优化

李京峰, 陈云翔, 项华春, 王 健

(1. 空军工程大学装备管理与无人机工程学院, 陕西 西安 710051;2. 中国人民解放军94354部队, 山东 济宁 272412)

0 引 言

军事装备内关键部件的意外失效不仅会导致作战任务进程中断甚至灾难性事故发生,还会增加维修保障成本,合理的维修决策和备件库存管理有助于确保关键部件安全、持续运行。随着检测技术的不断发展,视情维修作为一种有效手段已广泛应用于许多关键部件的维修保障工作中。其可根据检测到的部件退化状态信息及预设阈值,制定相关维修计划,并进一步为库存策略优化提供信息支持。

目前,大多数视情维修决策基于备件无限可用的假设,即维修工作的实施仅依赖于部件的退化状态信息,忽略了备件库存水平的影响;另一方面,备件库存管理主要依靠假设的备件需求分布,忽略了维修决策是备件需求产生的关键驱动因素这一内在逻辑。以上两点均与实际不符,因此,将视情维修与备件库存联合优化十分必要。

文献[8]对近年来关于不可修部件的维修与库存联合优化问题进行了系统性综述,其中文献[11-13]从成本角度验证了联合优化结果通常优于单一优化或不考虑关联性的顺序优化。文献[14]和文献[15]先后通过解析的方法研究了连续退化单部件系统、两部件系统的视情维修与备件订购策略联合优化问题。文献[16]针对退化过程符合Wiener过程的多部件系统,利用剩余寿命信息制定维修与库存策略,同时将遗传算法和蒙特卡罗仿真(Monte Carlo simulation, MCS)结合进行求解。文献[17]通过将问题转化为马尔可夫决策过程,研究了多部件系统的视情维修与备件库存联合优化问题。文献[18]则针对多部件系统退化监测信息不完全的情况提出一种部分可观测马尔可夫决策过程,解决了视情维修与备件选择的联合优化问题。

当前研究虽然在视情维修与备件库存联合优化问题上取得一定成果,但若在军事领域应用则忽略了以下现实问题:装备内关键部件在执行任务尤其作战任务过程中,由于工作环境复杂,通常会受到磨损、疲劳、腐蚀、过载、冲击等多种因素影响,因此最终的失效并非仅由自然退化引起,外部随机冲击等突发性因素同样会引起关键部件失效,而随机冲击带来的突发失效或自然退化增量将会改变原有维修和库存计划安排。文献[22-26]从综合考虑自然退化和随机冲击的退化建模、可靠性评估、剩余寿命预测、维修策略等方面开展了相关研究,但在视情维修与备件库存联合优化方面的进一步延伸却未有学者探讨。

因此,本文基于实际中普遍采用的定期检测策略,提出一种考虑随机冲击影响的多部件系统视情维修与备件库存联合优化模型。具体方法为:建立考虑随机冲击影响的退化模型,在首达时间的意义下推导出部件剩余寿命的解析概率分布,采用极大似然法估计模型参数;结合剩余寿命预测结果和随机冲击影响提出视情维修与备件库存联合策略,建立联合优化模型,利用粒子群优化(particle swarm optimization, PSO)算法和MCS进行求解;最后,通过实例分析验证本文模型的有效性,并对随机冲击参数进行敏感性分析。

1 退化模型与剩余寿命估计

1.1 问题描述与假设

考虑系统是由个类型相同且独立工作的部件组成,并且部件具有相同的退化特性和备件。为研究部件的退化机理,本文做出以下描述和假设。

(1) 假设采取定期检测策略,检测活动完美,能够完全得到各个部件的实际退化状态,单次检测成本为,检测间隔为Δ,检测时间可忽略不计。

(2) 随机冲击分为两类:冲击强度超过特定阈值的致命冲击,直接导致部件失效;冲击强度低于的非致命冲击,给部件带来退化增量。部件在任意时刻的退化总量()包括自然退化量()和由非致命随机冲击导致的累积退化量()。

(3) 部件的失效分为两种:如果退化总量()达到预设阈值,则发生软失效,亦称退化型失效;如果某次冲击强度超过阈值,则发生硬失效,亦称突发型失效。

1.2 自然退化模型

基于Wiener过程的退化模型由于能够描述多种典型产品的性能退化过程,且具有良好的计算性质,目前已被广泛应用于工程领域。因此本文选取Wiener过程对连续自然退化过程建模,提高模型的通用性,其表达式为。

()=(0)++()

(1)

式中:(0)表示部件的初始性能状态,由于Wiener过程是独立增量过程,根据独立增量过程的定义,(0)=0;和分别表示部件的漂移系数和扩散系数,反映部件的退化速率和波动程度;()表示标准布朗运动,反映退化过程的时变不确定性,且()～N(0,)。

当部件退化状态超过失效阈值时,认为部件失效,具体如图1所示。令()表示部件在时刻的状态()=的概率密度函数(probability density function, PDF),表达式为

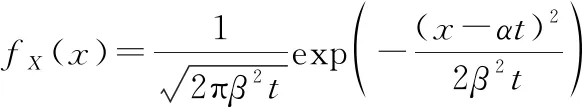
(2)

据此可得可靠度()为

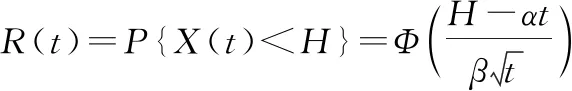
(3)

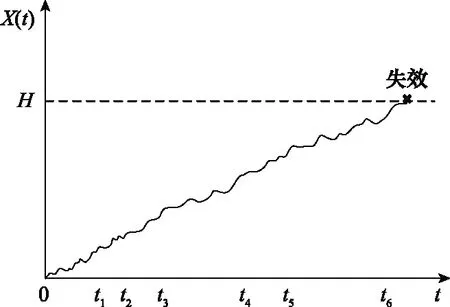
图1 自然退化过程Fig.1 Natural degradation process

1.3 随机冲击影响下的退化模型

假设随机冲击的到达过程遵循到达率为的齐次泊松过程(homogeneous Poisson process, HPP){(),≥0},则在任意长度为的时间间隔[,+]内,冲击次数为(=0,1,…)的概率分布为

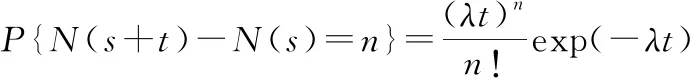
(4)

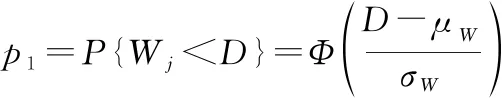
(5)

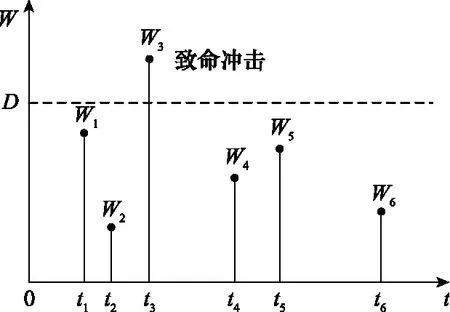
图2 随机冲击过程Fig.2 Random shock process

根据泊松过程的分解定理,两类冲击亦分别遵循到达率为和的HPP,且二者相互独立。令表示第次非致命冲击给部件退化造成的瞬时退化增量,其度量由冲击强度转换,即=,为转换因子,因此亦服从正态分布。综上可得,时间内由非致命冲击导致的累积退化量()为

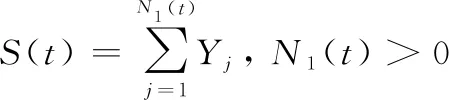
(6)

当()=时,()的概率分布函数()为

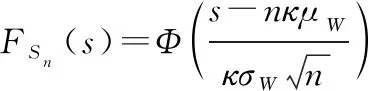
(7)

根据以上分析,对于同时经历自然退化与随机冲击的部件,退化过程如图3所示,其在时间内的退化总量()为

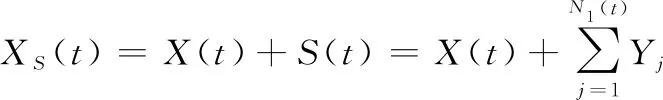
(8)

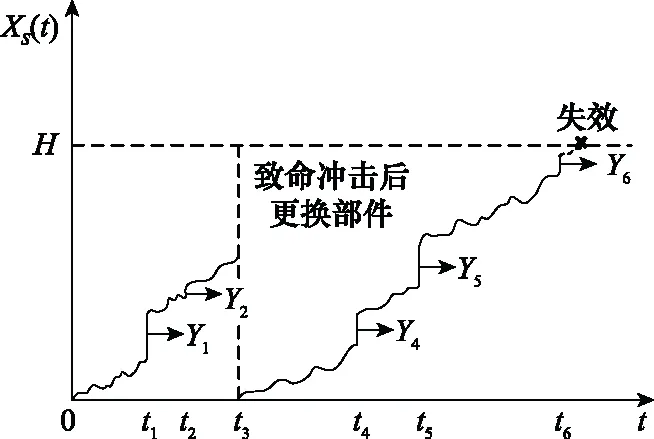
图3 随机冲击影响下的退化过程Fig.3 Degradation process under the effects of random shock

因此,部件在时间内不发生失效需满足的条件是,期间没有致命冲击且退化总量低于失效阈值。据此可得可靠度()为

(9)

1.4 剩余寿命估计

根据首达时间的概念,在当前时刻为时,部件的剩余寿命可以定义为

=inf{:(+)≥|()<}

(10)

已知仅考虑Wiener退化过程的部件剩余寿命PDF为

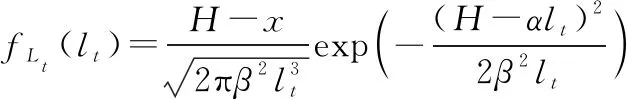
(11)

式中:表示时刻部件的实际退化量。

在求取考虑随机冲击影响的部件剩余寿命PDF时,利用文献[24]中的阈值转换思想将式(10)中的固定失效阈值转换为-(),结合全概率公式可得

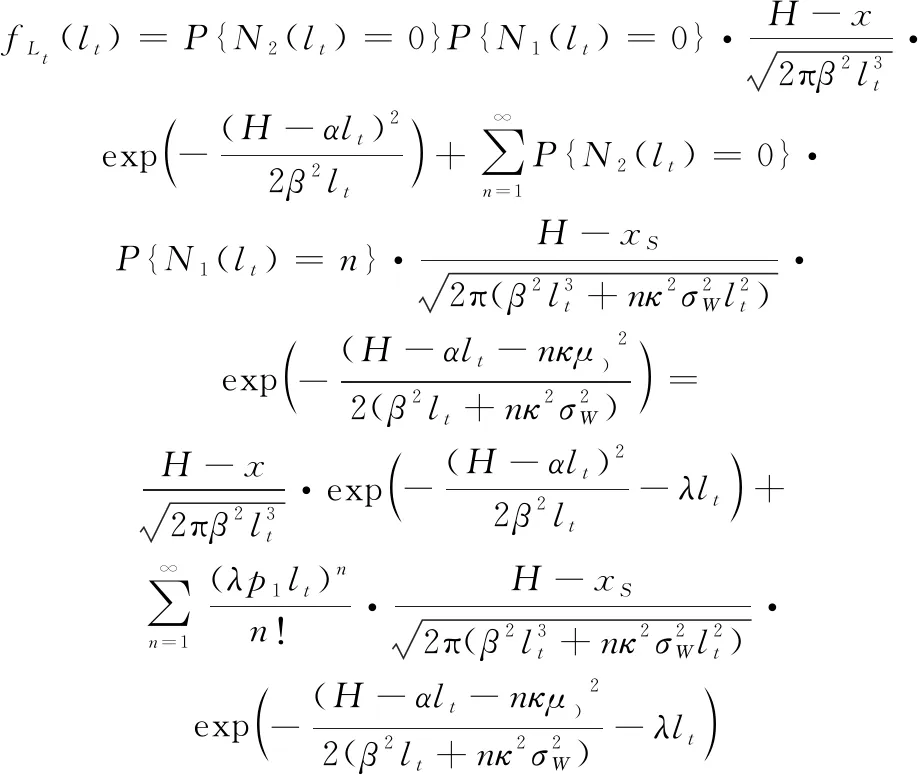
(12)

式中:表示时刻部件的总退化量。

由式(12)可得考虑随机冲击影响的部件剩余寿命的期望表达式为

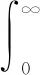
(13)

1.5 参数估计

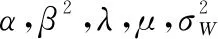
=[Δ+1,Δ+2,…,Δ+]

(14)

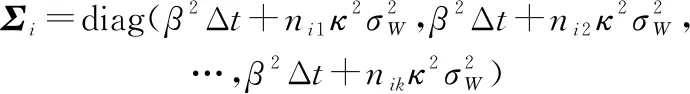
(15)

式中:表示部件第个检测间隔内发生的非致命冲击的次数。令Δ=[Δ1,Δ2,…,Δ]表示所有部件的退化检测数据,则Δ的对数似然函数可表示为

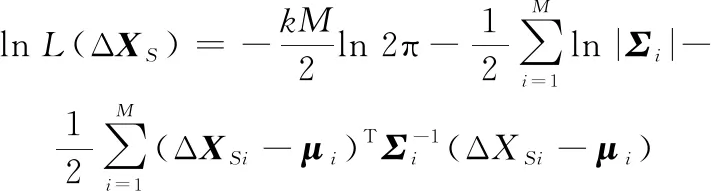
(16)

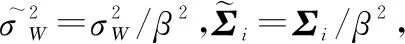
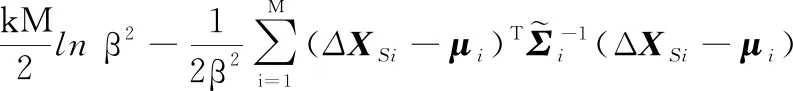
(17)

然后得到ln(Δ)关于和的一阶偏导数分别为

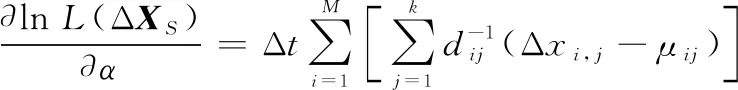
(18)

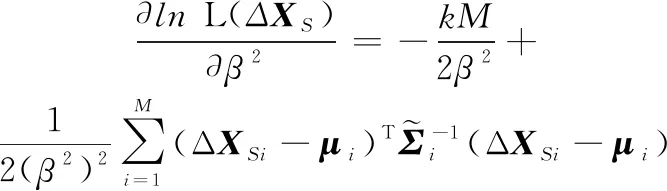
(19)

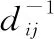
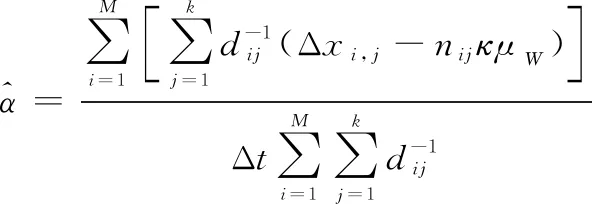
(20)

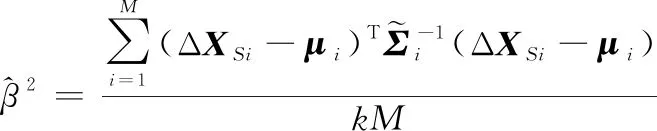
(21)

2 视情维修与备件库存联合策略

2.1 视情维修策略

本文采取基于定期检测的视情维修策略,具体如下。

(1) 若,≥或者在时间间隔(-1,]内任一≥,则部件失效,在时刻进行失效性更换,成本为。

(2) 若在时间间隔(-1,]内未发生致命冲击且,<,根据状态检测数据获得参数估计值,然后由式(13)计算得部件在时刻的期望剩余寿命为E(,)。设预防性更换的剩余寿命阈值为,为防止部件在下一检测间隔内失效,令≥Δ。若E(,)≤,则部件进行预防性更换,成本为,否则不采取任何操作。

2.2 备件库存策略

无论失效性更换还是预防性更换均会产生换件需求,从而消耗库存中的备件。本文以目前较为通用的库存策略(,)为基础阐述库存消耗与补充过程,具体如下。

(1) 当产生失效性更换或者预防性更换的换件需求时,首先要检查库存水平,若库存水平能满足所有换件需求,则正常进行更换并更新当前库存水平。若库存水平小于等于则发起订购-个备件的指令,经过固定的备件交货期后补充库存。

(2) 当换件需求数量超过当前库存水平时,则优先保障失效性更换,同时发起订购指令,到货后优先保障欠件更换。由于备件数量不足导致的单个部件单位时间停机损失成本为。

(3) 假设库存补充过程的单次订购成本为,备件单价为,单位时间单个备件存储成本为。

图4为维修与库存联合运行机制示意图,展示了维修过程与库存消耗、补充过程之间的关系,并给出了相关统计数据的更新和计算方法。

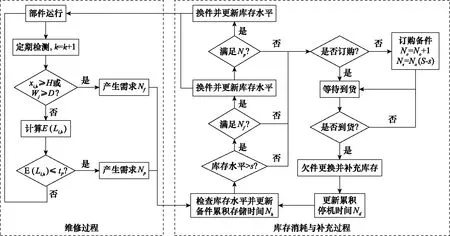
图4 维修与库存联合运行机制Fig.4 Joint operation mechanism of maintenance and inventory

3 联合优化模型与求解算法

3.1 联合优化模型

对于视情维修与备件库存联合优化问题,频繁的检测、更换以及较高的库存水平会导致高昂的维修与库存成本,反之成本虽会降低,但系统失效风险会上升,备件保障能力会下降。因此,为了平衡检测、更换、订购、存储成本与缺件风险,本文以单位时间内平均费用成本最低为目标,确定最优联合策略对应的决策变量组合(Δ,,,)。模型表示如下:

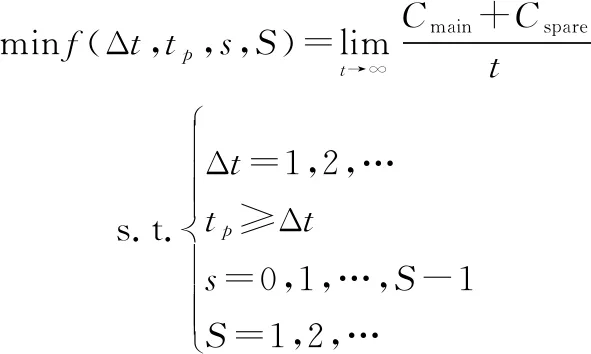
(22)

式中:表示维修成本;表示库存成本,具体计算公式分别为

=+++

(23)

=++

(24)

式中:,,,,,,分别表示系统运行周期内的检测次数,失效性更换次数,预防性更换次数,所有部件累积停机时间,备件订购次数,累积订购备件数,所有备件累积存储时间。

3.2 求解算法

由于维修过程以及库存的消耗与补充过程较为复杂,显式地解析出目标函数与决策变量之间的关系非常困难,因此可以利用MCS仿真系统中部件退化,以及维修与库存的动态变化过程。同时,利用PSO算法在搜索空间内快速求得最优联合策略。本文设计的PSO-MCS优化算法具体如下。

设定相关参数,初始化个粒子的速度和位置(Δ,,,),=1,2,…,。

对于每个给定的粒子,通过次MCS计算出对应的适应值(Δ,,,),仿真过程如下:

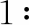
采用增量采样法仿真部件自然退化增量和在(-1,]内产生的随机冲击;

若经检测(-1,]内产生的任一随机冲击强度≥,或者退化总量()≥,则产生失效性更换需求。检查库存水平,若能满足换件需求则进行更换,否则欠件,发起订购指令。期间记录并更新相关数据;

若所有<且()<,计算期望剩余寿命(),若()≤,则产生预防性更换需求。检查库存水平,若能满足换件需求则进行更换,否则欠件,发起订购指令。期间记录并更新相关数据;

等待到货期间其余正常运行部件仍按照步骤2.2至2.4更新,备件到货后若有欠件,则进行欠件更换,然后补充库存,更新库存水平;

判断运行时间是否达到设定周期,若达到则转入步骤27,否则令=+1,返回步骤22;

计算第次MCS的平均费用率,返回步骤21进入下一次循环,直至仿真次;

最终得到粒子对应的适应值:

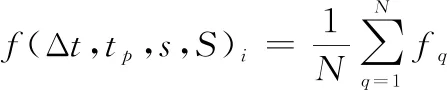
end。

搜索确定当前每个粒子的个体最优解以及整个粒子群的当前整体最优解。

基于和更新群体中每个粒子的速度和位置。

判断是否满足最大迭代次数,若满足则输出最优解,以及对应的最优联合策略(Δ,,,),否则转入步骤 2。

4 实例分析

4.1 模型验证

陀螺仪是惯性导航平台的关键组成部分,在军事装备、航空航天等领域有着重要的作用。实际使用过程中,受陀螺转子高速旋转磨损和外部随机冲击等影响,陀螺仪漂移系数逐渐增大,性能发生退化,最终导致失效。因此,通过定期检测获取陀螺仪退化数据,建立退化模型,估计剩余寿命,在此基础上确定合理的维修与库存联合策略,对保证任务顺利进行和降低维修保障成本具有重要意义。

由于实际执行任务期间随机冲击数据量化困难,通常检测获取的实际退化量已经夹杂着随机冲击的影响,故而很难将部件自然退化与外部随机冲击剥离。因此,本文以6台独立工作的某型装备内陀螺仪的冲击退化试验数据为基础,结合仿真验证本文模型。该数据记录了按照通电时间,每天通过检测设备获取的6台陀螺仪50天漂移系数退化数据,具体如图5所示。按照该型陀螺仪技术指标,选择失效阈值为=9°/d。

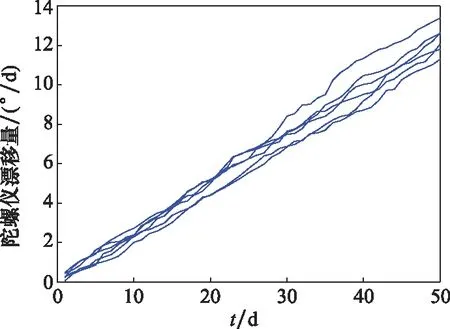
图5 陀螺仪漂移系数退化数据Fig.5 Degradation data of gyro drift coefficient

根据冲击退化试验数据,采用本文参数估计方法得到的退化模型参数估计结果为(,,,,)=(0.12,0.05,1.00,1.21,0.19)。将此结果用于后续仿真优化中退化过程的参数设定,保证优化结果的有效性。联合优化模型和PSO-MCS优化算法涉及的初始参数值如表1所示。

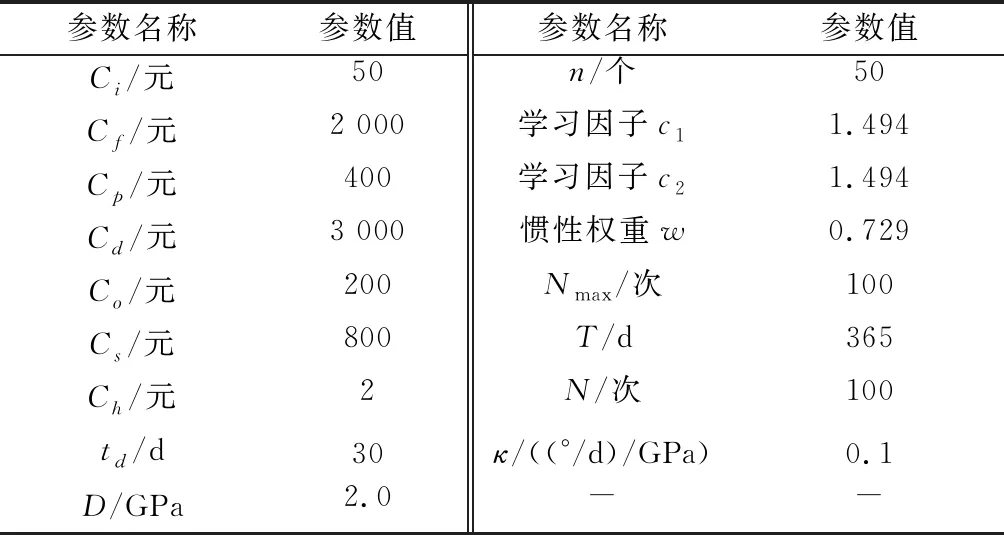
表1 参数设置

通过仿真优化得到最优平均费用率为256.05元/天,对应的4个决策变量的最优组合为(Δ,,,)=(5,8,6,29),由此确定了考虑随机冲击影响的视情维修与备件库存最优联合策略,实验结果如图6所示。

图6 考虑随机冲击影响的优化结果及库存水平变化Fig.6 Optimization results and inventory level changes considering effects of random shock

4.2 对比分析

为进一步证明工作在复杂环境中的关键部件,其视情维修与备件库存联合策略考虑外部随机冲击影响的必要性,以及本文提出模型的有效性,将本文模型(简称为M)与仅考虑自然退化(基于Wiener过程)的视情维修与备件库存联合策略模型(简为称M)进行对比。需要说明的是,M所用退化试验数据为另一组没有随机冲击的6台陀螺仪漂移系数退化数据,M实验结果如图7所示。

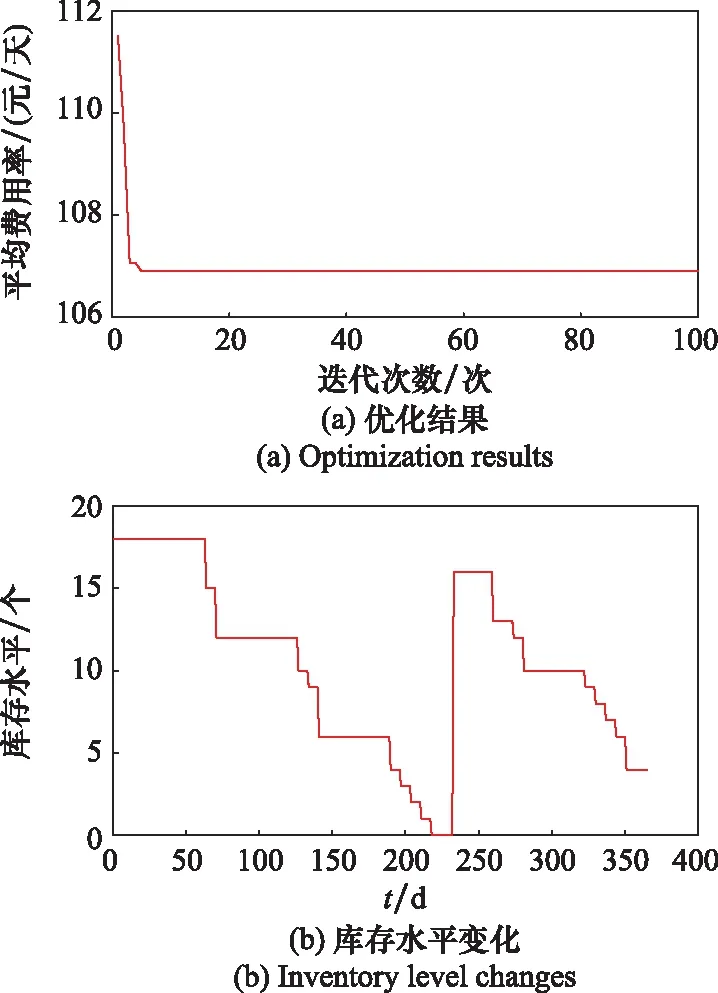
图7 仅考虑自然退化的优化结果及库存水平变化Fig.7 Optimization results and inventory level changes only considering natural degradation

结果表明,M的最优平均费用率为106.91元/天,对应的4个决策变量的最优组合为(Δ,,,)=(7,10,2,18)。由此可见,相比于M,不受外部随机冲击影响的M的维修保障成本明显下降,检测间隔和预防性更换阈值增大,安全库存和最大库存减小,说明了随机冲击会显著改变视情维修与备件库存联合策略以及相关成本。

关于随机冲击造成以上显著改变的内在原因,本文从可靠度和剩余寿命两方面进行深入剖析,结果如图8所示。

图8(a)展示了由式(3)和式(9)得到的M和M的可靠度曲线,图8(b)以陀螺仪1为例展示了在不同退化检测时间点上,由式(11)和式(12)估计的M和M的剩余寿命PDF以及期望剩余寿命,并给出了对应的实际剩余寿命。观察可知,M中的陀螺仪可靠度出现明显下降的时间比M中的陀螺仪要提前近40天,说明随机冲击会加速陀螺仪的退化。加速退化的结果会进一步影响陀螺仪剩余寿命的估计,进而对最优策略(Δ,,,)的制定产生影响。同时,由于陀螺仪更换频率加快,以及随机冲击带来更大的失效不确定性,维修保障成本也会随之增加。至此,得到了M和M优化结果差距的内在原因,同时充分证明了本文构建模型的意义及必要性。

另一方面,为证明本文提出模型的有效性,将M的最优联合策略(Δ,,,)=(7,10,2,18)应用于M,得到M的平均费用率为3 740.87元/天,远远超过M的最优平均费用率256.05元/天。这是因为M并未考虑随机冲击影响,将其最优联合策略应用于M理论上会造成停机数量的增加,从而导致平均费用率急剧上升。100次MCS的实验结果验证了该假设,具体结果是:M在其最优联合策略下的平均停机数为0,M在M最优联合策略下的平均停机数为14。这一结果表明本文构建模型能有效改善联合策略,减少停机数量,降低维修保障成本。

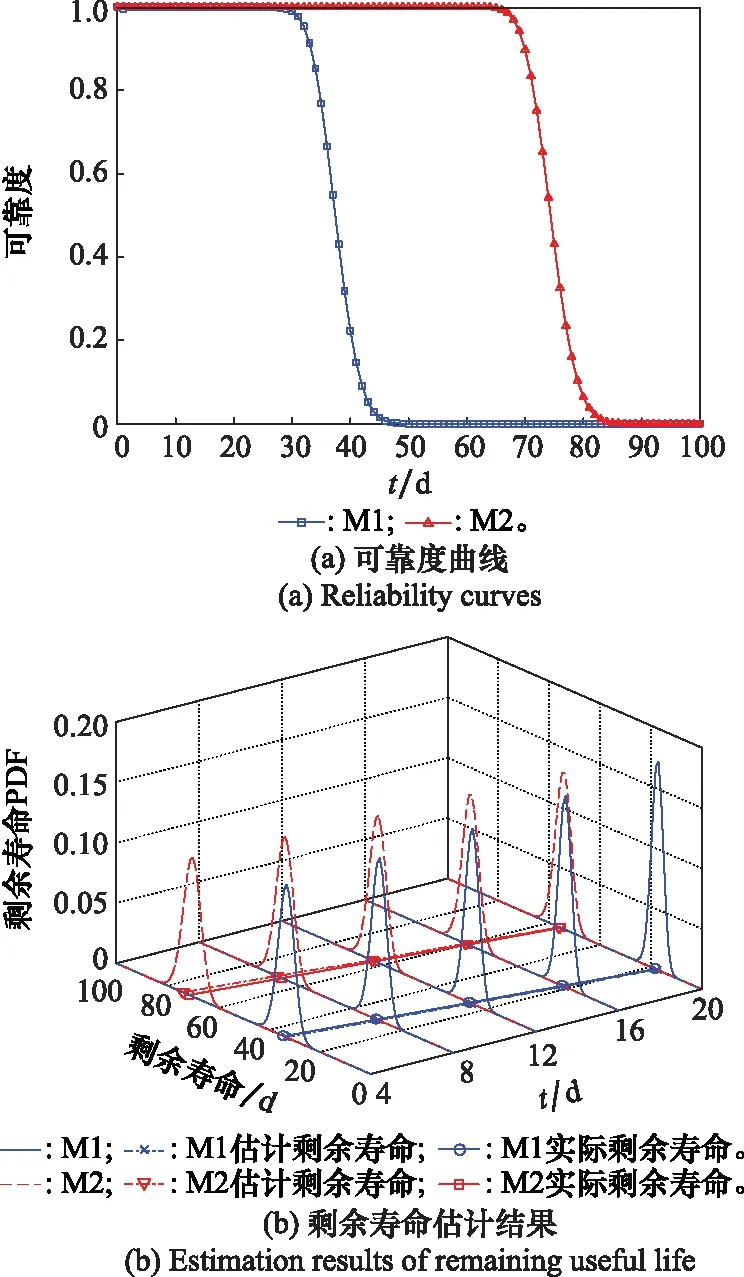
图8 可靠度曲线与剩余寿命估计结果Fig.8 Reliability curves and estimation results of remaining useful life

4.3 敏感性分析

接下来进一步探究随机冲击参数对M优化结果的影响。将随机冲击参数,,分别独立调整,得到M优化结果对不同参数的敏感程度,具体如表2所示。

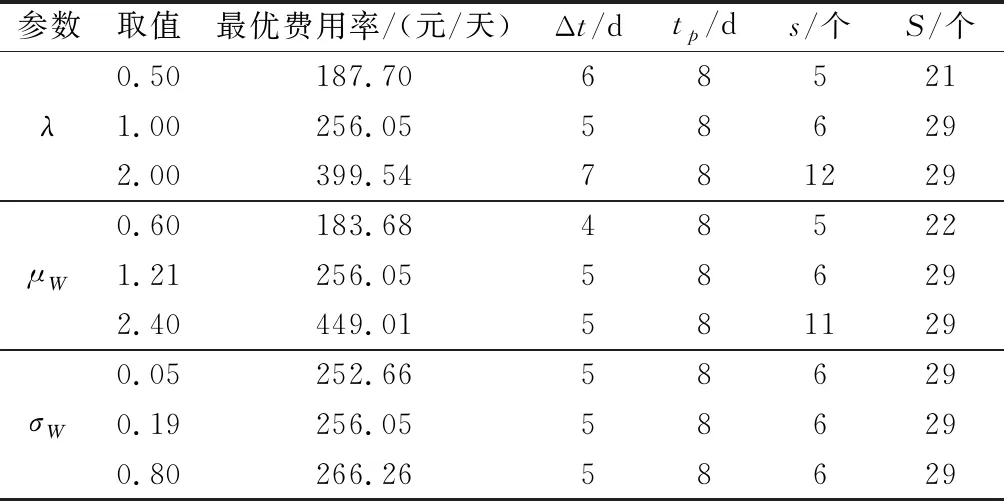
表2 不同随机冲击参数对应的优化结果

由表2可知,反映随机冲击到达率的参数对优化结果影响较大,最优费用率和安全库存与的变化呈明显正相关关系。这是因为在冲击强度不变的情况下,冲击频率的增加或减少将直接影响陀螺仪的实际退化速度,进而影响陀螺仪的更换频率,最终导致费用率发生改变。同时,由于安全库存的设置与订购成本、存储成本和停机成本高度相关,为保证联合优化模型达到最优费用率,安全库存必然会随着的变化发生明显改变。

反映冲击强度均值的参数对优化结果影响同样较大,最优费用率和安全库存与的变化亦呈明显正相关关系。这是因为在冲击到达率和冲击强度标准差不变的情况下,的变化除了会影响陀螺仪的实际退化速度,还会影响突发型失效发生的概率,从而导致与相似的结果。但是,反映冲击强度标准差的参数对优化结果没有明显影响。这是因为经过式(15)等的转换,对陀螺仪退化增量的贡献相比于和可忽略不计。

以上敏感性分析结果表明,随机冲击参数对联合优化策略和维修保障成本的影响不可忽视,尤其λ和μ是产生影响的关键因素。

5 结 论

本文针对在复杂环境中工作的关键部件,基于定期检测策略提出了一种考虑随机冲击影响的多部件系统视情维修与备件库存联合优化模型,拓展了联合优化模型在复杂环境中的应用,且模型具有一定的通用性。建立了随机冲击影响下的退化模型及可靠度函数模型,在首达时间的意义下利用阈值转换思想推导出了剩余寿命PDF,采用极大似然法估计了退化模型参数。制定了考虑随机冲击影响的视情维修与备件库存联合策略,以平均费用率最低为目标建立了联合优化模型,并设计了PSO-MCS优化算法。以陀螺仪为例验证了复杂环境中模型考虑随机冲击影响的必要性以及模型的有效性,同时敏感性分析结果表明随机冲击对多部件系统视情维修与备件库存联合优化结果具有重要影响。进一步说明了本文提出模型具有潜在的实际应用价值。

由于现有研究包括本文均在固定检测周期下开展视情维修与备件库存联合优化,而在部件退化后期的检测间隔内往往更易发生失效性更换,造成较大经济损失。因此,在下一步工作中,将研究如何利用部件剩余寿命信息确定合理的可变检测周期,并对动态检测周期视角下的视情维修与备件库存联合优化问题深入探讨。