基于进化PSO算法的稀疏捷变频雷达波形优化

杜思予, 全英汇, 沙明辉, 方 文, 邢孟道

(1. 西安电子科技大学电子工程学院, 陕西 西安 710071; 2. 北京无线电测量研究所, 北京 100854; 3. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

particle swarm optimization (PSO) algorithm

0 引 言

捷变频雷达(frequency agility radar, FAR)脉间频率随机跳变,能够减少干扰机侦收真实信号载频的概率,有效规避大部分窄带瞄准式干扰、前拖欺骗式干扰等,显著提高雷达抗干扰能力。文献[1]在FAR的基础上进一步改进,提出一种具有更小数据率、更高频谱利用率的稀疏捷变频(sparse frequency agility, SFA)雷达。针对频率捷变体制雷达多普勒不连续的问题,文献[2]引入压缩感知(compressed sensing, CS)理论实现相参积累。然而,采用CS理论进行信号稀疏重构时,字典矩阵的选取直接影响原始信号重构的效果。现有文献中针对SFA雷达信号的优化方法较少,亟待进一步研究。文献[4]考虑局部最优和全局最优的关系,采用模拟退火(simulated annealing, SA)算法对多维捷变信号进行优化,虽然该方法寻优精度较高,但对于复杂的字典矩阵来说收敛速度过慢。文献[5]将粒子群优化(particle swarm optimization, PSO)算法引入波形自适应优化设计中。文献[6]讨论了SA算法的多种改进方式。但两者都没有解决算法本身的缺陷。基于此,考虑到雷达信号和字典矩阵的自身特性,本文将SA算法一定概率接受差解的思想引入PSO算法,在保证优化效果的前提下,综合收敛速率快和跳出局部最优达到全局最优解的优势,并利用所提进化PSO算法对SFA雷达信号进行优化设计,在不破坏捷变体制带来的抗干扰能力前提下,提高待恢复目标的稀疏度上限以及回波信号稀疏重构的精确性和稳定性。

1 信号模型

SFA雷达发射载频稀疏跳变的脉冲,如图1所示。相比传统频率捷变雷达,SFA雷达发射带宽内的部分频率,因此具有较短的相参处理时间(coherent processing interval, CPI),在不损失距离分辨率的前提下尽可能降低频谱资源消耗。

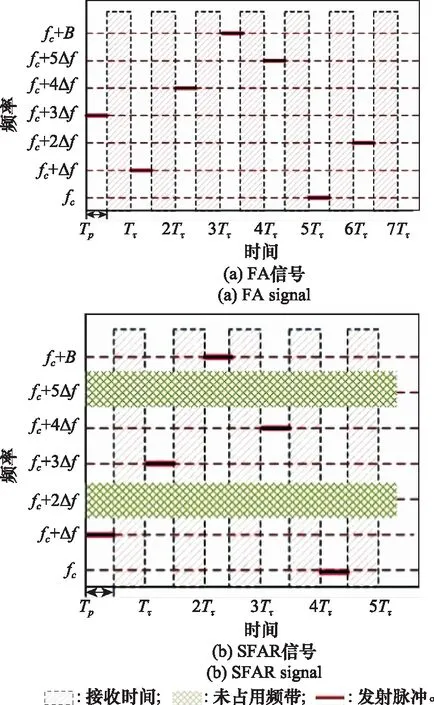
图1 FA和SFAR信号示意图Fig.1 Schematic diagram of FA signal and SFAR signal

图1中,为脉冲重复周期,为脉冲宽度。

假设一个CPI内共发射个脉冲,总跳频数为,且满足>的稀疏跳频条件。跳频总带宽设为,初始载频为,第个脉冲的载频为∈[,+](=0,1,…,-1)为从总跳频集合中随机选取的个频率集合,定义有效带宽和有效跳频间隔Δ分别为

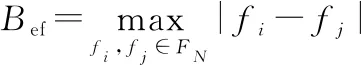
(1)

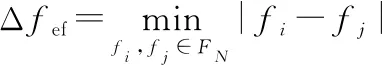
(2)

同一个CPI内的所有脉冲均采用线性调频调制波形,第个脉冲表示为

(3)

式中:=为线性调频率;窗函数可表示为

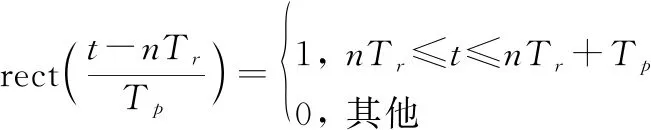
设跳频码字为()∈[0,1,…,-1],用于选取稀疏的随机跳变子载频。故第个脉冲的频率可以表示为

=+()Δ

(4)

假设观测场内总共存在个目标,则第个脉冲的回波信号的表达式为

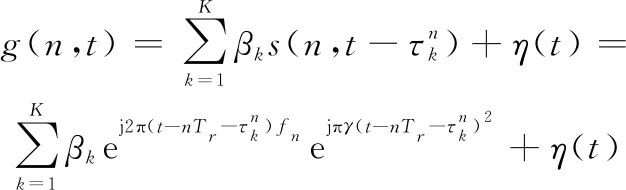
(5)

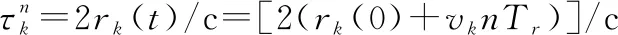
考虑第个脉冲的回波信号在一个快时间(,)=+内以1的采样速率进行采样,其中=1,2,…,表示采样序号,=||。第个脉冲回波信号采样后,经过混频和脉压处理,匹配滤波的输出信号表达式为

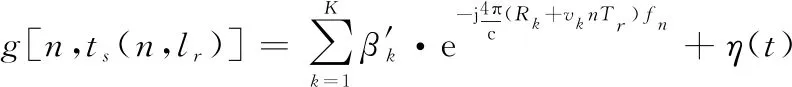
(6)

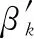
2 SFA雷达信号优化设计

考虑到SFA雷达信号脉冲间载频随机跳变,导致回波信号多普勒不连续,无法直接采用脉压处理进行动目标检测(moving target detection, MTD)。在实际的雷达探测场景中,目标满足稀疏特性。因此,采用CS理论成为一种有效的参数估计方法。为了保证雷达目标探测性能,在求解CS模型时,需要字典矩阵满足正交特性,而字典矩阵的选取和发射信号的特性有关。

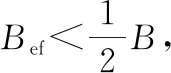
2.1 建立优化模型

将式(4)代入式(6),可得

(7)

基于CS理论,将观测场景分别沿距离向和速度向划分为个独立的高分辨距离单元和个高分辨速度单元,构建高分辨距离-多普勒二维网格平面,回波信号可以改写为

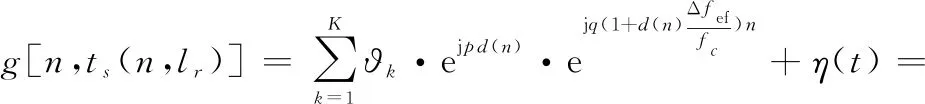
(8)

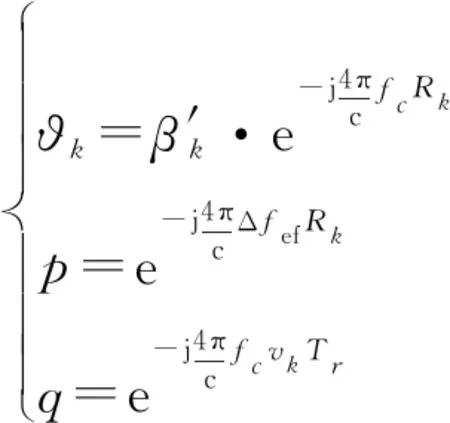
(9)

第-1个采样时刻和第个采样时刻之间的距离间隔称为一个粗分辨距离单元。在一个CPI内,对不同粗分辨单元上的采样数据分别处理。因此,考虑一个粗分辨单元中,个脉冲回波信号组成一组字典数据:

(10)

因此,构建出SFA雷达回波信号的压缩感知模型:

(11)

将其改写为

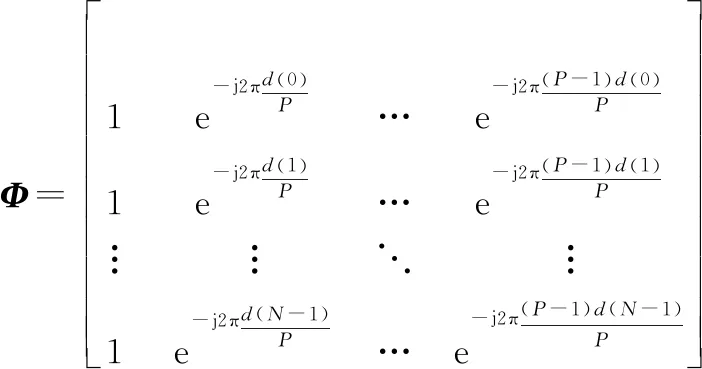
(12)

式中:∈为稀疏向量;∈×为字典矩阵;∈×为高分辨距离字典矩阵;表示矩阵的第列;∈×为多普勒字典矩阵;定义◎表示运算◎=[diag(),diag(),…,diag()]。

Candes和Tao提出的约束等容特性(restricted isometry property, RIP)特性以及Mallat和Zhang等人提出的互不相干性(mutual incoherence property, MIP)都是衡量字典矩阵正交性质的重要准则。字典矩阵的最大相干系数定义为

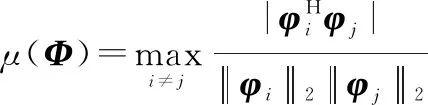
(13)

式中:,为字典矩阵中不同的列。当()足够小时,称矩阵具有MIP。换言之,字典矩阵趋于正交时,CS算法能够稳定精确地恢复任意稀疏度的向量。

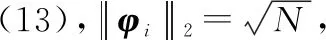
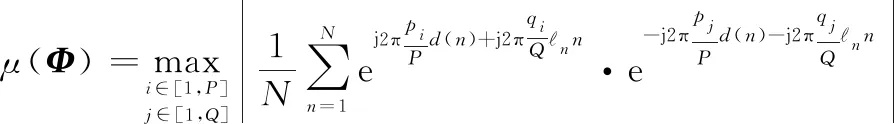
(14)

同时,考虑到稀疏跳频带来的有效带宽过小以及有效跳频间隔Δ较大的问题,对子载频的选取条件进行一定的限制,使有效带宽和有效跳频间隔Δ满足

|-1-|≥||≥|-1-|

(15)

min|-|≤|Δ|≤min|-|

(16)

式中:,为给定的正实数;,∈。

因此,建立优化模型为

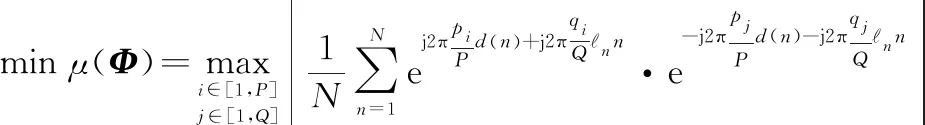
(17)

2.2 基于进化PSO算法求解优化模型

PSO算法是1995年Eberhart和Kennedy基于对鸟群觅食行为研究的基本概念提出的一种迭代优化算法。PSO算法操作简单、收敛速度快,能够有效解决本文优化矩阵维度过大导致的迭代效率低的问题。然而PSO算法存在收敛早熟,易于陷入局部最优导致寻优精度不高等缺陷,因此本文引入SA思想,利用其一定概率暂时接受一些劣质解的特性改进标准PSO,实现跳出局部最优而最终达到全局最优解的目的。

本文基于进化粒子群算法求解优化模型式(17)的具体流程如下:

设置SFA雷达信号相关参数;设置PSO相关参数:最大迭代次数,当前已迭代次数,目标函数寻优粒子个数,维度,根据解的可行域随机初始化粒子的位置和速度;设置SA相关参数:初始温度,温度衰减因子,当前温度=·。

初始化SFA雷达信号的载频跳变序列()(=1,2,…,),使其满足式(17)中的约束条件,根据式(12)生成字典矩阵,并利用式(14)定义目标适应度函数。

计算初始位置各粒子的适应度,作为当前个体最优值，其对应的位置记为,比较所有粒子的适应度,当前全局最优值对应的位置记为。

根据PSO的更新规则对各粒子当前的位置和速度进行更新,并计算更新位置后各粒子的适应度以及其中最优适应度,分别与当前个体最优值和当前全局最优值比较,当新旧位置适应度之差Δ<0时,则粒子进入新位置;否则转下一步。其中,为权重系数,为学习因子,为[0,1]的随机数,PSO的速度和位置更新规则表达式为

+1=ω+(-)+(-)+1=+

(18)

根据新旧位置适应度之差Δ计算退火策略的接受概率值,粒子以概率决定是否进入新位置。其中,的概率分布表达式为

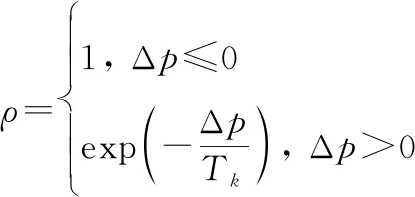
(19)

迭代次数自加=+1,当前温度进行退温操作+1=·。

判断算法是否收敛或是否达到终止条件,如果满足,执行步骤8;否则跳转到步骤4继续执行到步骤6。

输出全局最优值对应的位置,即最优跳频码字()。

3 仿真验证

3.1 算法有效性验证

为了验证所提算法的有效性,分别选取文献[4]中采用的SA算法和标准PSO算法作为对比算法。仿真时采用线性调频的SFA雷达信号,设置总跳频数=64,脉冲数=16,初始载频=14 GHz,跳频总带宽=576 MHz,约束条件取=08,=2,随机生成满足约束条件的载频序列。

图2和图3分别是采用文献[4]中算法和标准PSO算法得到的目标函数优化曲线。可以看出,文献[4]中算法虽然能够使目标函数收敛到最优值,但需要迭代大约450次才能达到收敛;而标准PSO算法虽然经过7次迭代后即可收敛,但容易陷入局部最优解而找不到全局最优解。

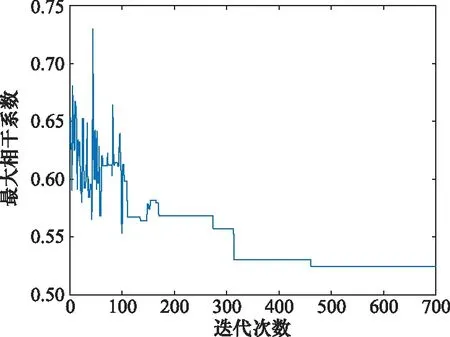
图2 文献[4]中算法优化结果Fig.2 Optimization result of algorithm in literature [4]

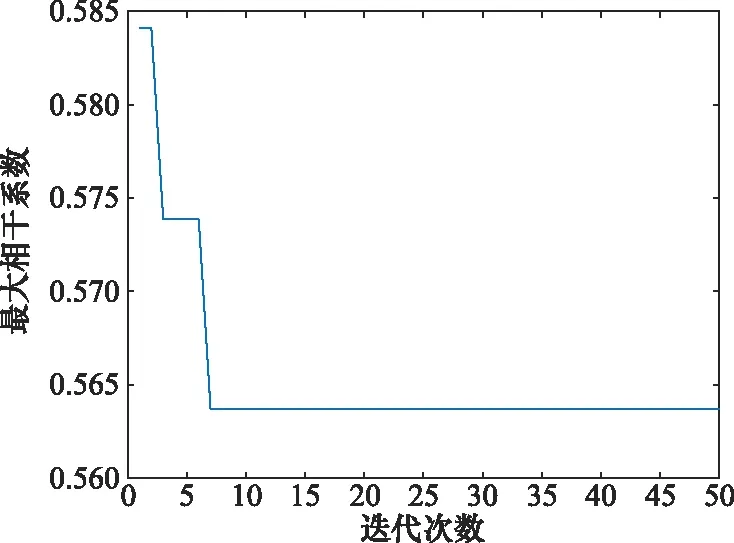
图3 标准PSO算法优化结果Fig.3 Optimization result of the standard PSO algorithm

利用本文所提进化PSO算法对信号进行优化,设置最大迭代次数为500次,进行仿真实验,由于PSO算法收敛较快,因此在仿真时增加终止条件的判定,避免算法无效迭代,结果如图4所示。

从图4可以看出,发射信号对应的字典矩阵随着迭代次数增加,最大相干系数明显下降,正交性提高。并且,该算法只需迭代41次就能达到收敛,效率远大于SA算法;概率接受劣值的设计也能够使其避免像PSO算法一样陷入局部最优解,寻优精度优于标准PSO算法。表1直观给出3种算法的对比结果。

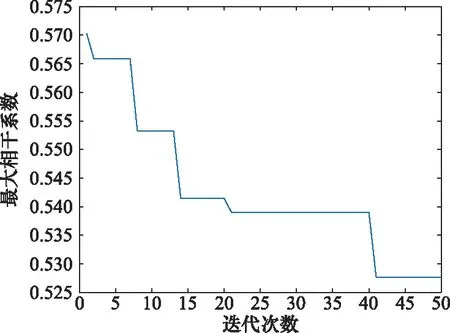
图4 目标函数优化曲线Fig.4 Optimization curve of the objective function

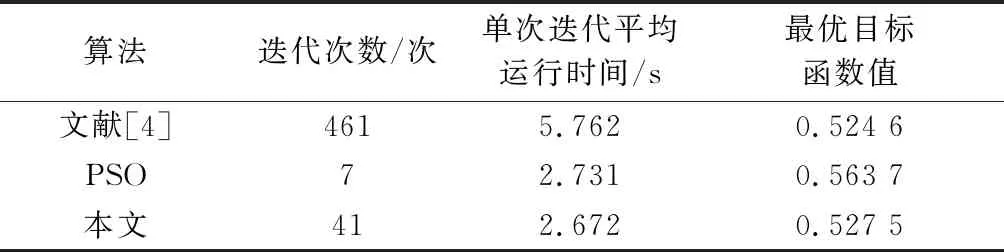
表1 3种算法比较

3.2 脉冲个数和总跳频数对信号重构的影响

固定总跳频数=64,分别选取脉冲个数=16,32,50作为SFA雷达发射信号,并采用上文所提进化PSO算法进行优化,对比结果如图5所示。随着脉冲数目增多,算法的运行速率大大下降。

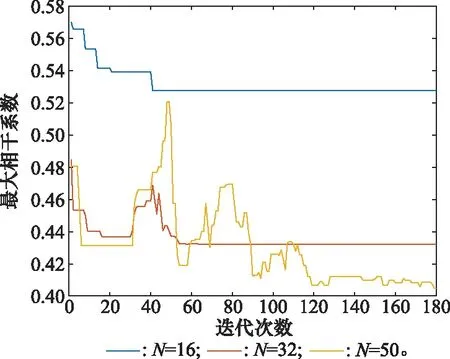
图5 不同脉冲数的优化结果Fig.5 Optimization results of different pulse numbers

固定脉冲数=16,分别选取总跳频数=32,64,80作为SFA雷达发射信号,采用进化PSO算法进行优化,结果如图6所示。随着总跳频数目增多,算法运算速度越慢。

从图5和图6可以看出,算法的运行时间由脉冲数和总跳频数决定,载频选取过“稠密”和“稀疏”都会影响算法运行效率。并且,当脉冲数目越多,即总跳频数越少,信号重构时字典矩阵的正交性越强。换言之,载频稀疏性和字典矩阵正交性是相对的,因此在实际应用中要综合考虑两者的特性,适当折中选取脉冲个数,在保证信号重构的精度前提下,尽可能减小CPI,降低数据率,减少频谱资源浪费。

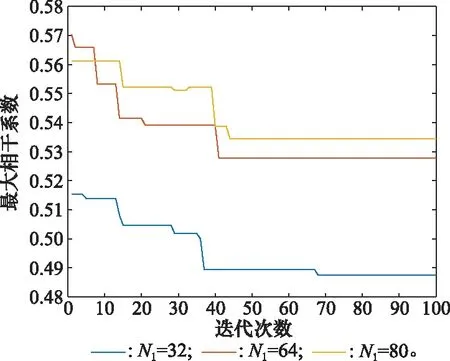
图6 不同跳频数的优化结果Fig.6 Optimization results of different frequency numbers

3.3 算法对信号重构的影响

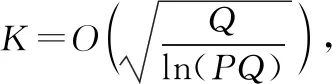
观测场内两个目标位置分别为(4 000 m, 4 001.56 m),速度分别为(33.5 m/s, 50 m/s)。设置总跳频数=128,脉冲数=64,其他参数设置同上,采用进化PSO算法优化。由于字典矩阵维度较大,仅记录中间列与其他列之间的相关系数,优化前后的字典矩阵相关性对比如图7所示。

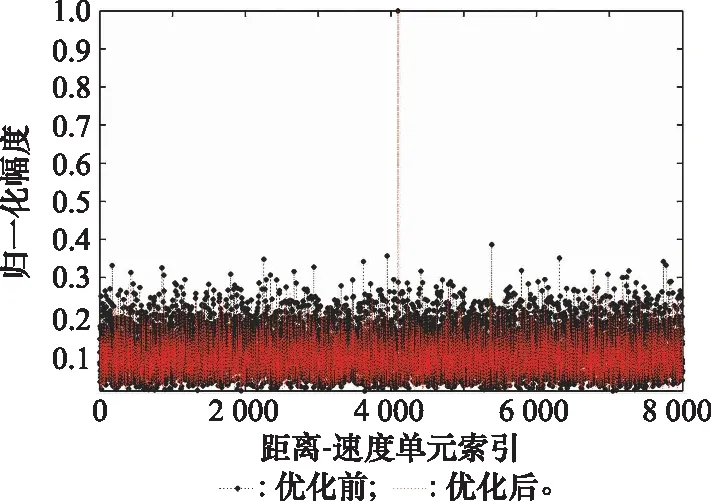
图7 优化前后相关性对比(中间列)Fig.7 Correlation comparison before and after optimization (middle column)

从图7可以看出,优化后的字典矩阵相关性明显下降,得到优化后的字典矩阵最大相干系数为0.31。根据定理1可知,基于上述参数,在一个粗分辨单元内能够精确恢复不超过两个目标。稀疏重构结果如图8所示,目标距离为(4 000 m,4 002 m),速度为(33.48 m/s,50.22 m/s),误差均小于0.5%。

选取信噪比SNR为-15 dB和-5 dB,对优化前后信号进行重构,仿真结果如图9所示。

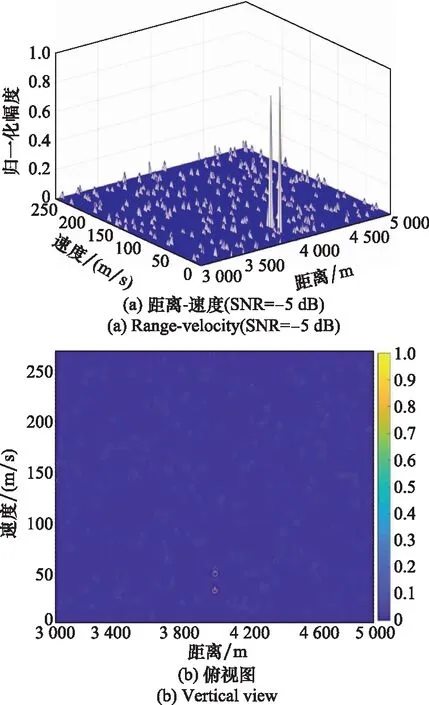
图8 优化后信号回波重构结果Fig.8 Reconstruction results of echo signal after optimization

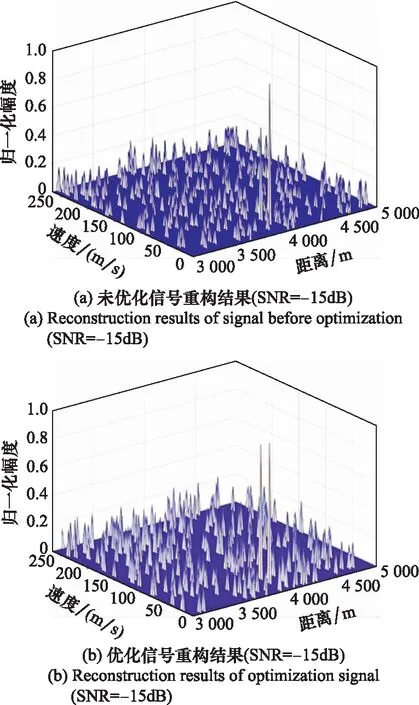
图9 不同信噪比重构结果Fig.9 Reconstruction results of different signal to noise ratio

对比图8和图9可以看出,基于进化PSO算法对SFA雷达信号优化结果与信噪比无关,仅是选取的重构算法会受到信噪比的影响。而低信噪比会使未优化的信号幅度受到一定影响,但测距和测速的精度不变。

4 结 论

本文主要针对频率捷变体制雷达进行信号优化设计。首先将稀疏载频特性引入到频率捷变体制中,形成具有更小数据率、更高频谱利用率的SFA雷达信号;然后针对SFA雷达信号,从回波信号稀疏重构的角度,最小化字典矩阵正交性,结合SA算法和PSO算法各自的优势,实现SFA雷达发射信号的优化设计。本文所提优化方案能够迅速收敛到最小相关系数,且优化精度较高。优化后的信号保留了频率捷变信号的抗干扰特性,确保了稀疏重构的稳定性和精确性。