基于稀疏重构的海杂波抑制和目标提取算法

李文静, 李卓林,*, 袁振涛

(1. 北京无线电测量研究所, 北京 100854; 2. 空军研究院, 北京 100085)

0 引 言

强杂波环境下的微小目标探测一直都是雷达目标检测、跟踪的难题。由于目标距离远、杂波背景强、雷达分辨率低等因素影响,有效的目标信号被杂波所淹没,接收信杂比较低,这都对雷达的探测性能提出了很高的要求。传统杂波抑制算法如动目标显示(moving target indication, MTI)等通过回波对消,具有一定的固定杂波抑制能力,但当目标处于海杂波、云雨杂波等运动杂波环境中时,运动目标的多普勒频率有可能落在杂波频率范围内,传统算法就产生了局限性,难以满足改善因子的需求。对此,亟需研究新的杂波抑制算法来实现复杂背景下的目标探测。

杂波抑制的关键在于确定能区分目标回波与杂波的不同特征。传统算法主要利用回波的幅度特性、相关性来进行杂波抑制和目标检测,如利用目标起伏特性进行帧间积累，或者通过一些变换如分数阶傅里叶变换(fractional Fourier transform,FFT),Hilbert变换等获取目标的特征,使之与杂波有所区分。近年来,许多研究人员提出了其他杂波抑制方法,如通过可调Q小波对回波进行分解,根据目标和杂波震荡的不同特性提取目标的有效信息;基于海面的分形和混沌特征对海杂波进行短期预测,并利用预测误差实现目标检测;通过适当的时频变换,克服了傅里叶变换时域、频域分离的缺点,根据杂波和目标回波在时频域的不同表现特征进行杂波抑制和目标检测;将人工智能技术引入到海杂波背景下的目标探测问题中,构建合适的神经网络,对杂波和目标进行识别。

随着稀疏分解和压缩感知等理论的不断发展,许多国内外专家学者都对此进行研究。信号的稀疏表示可以看作为将信号在稀疏域(稀疏基)上的一种映射,在该稀疏基上,通过尽可能少的非零变换域元素来表示信号的有用信息。但在海杂波等复杂背景下进行目标探测时,使用单一字典对信号进行稀疏分解,即稀疏成分分析(sparse component analysis,SCA),往往难以有效区分杂波和目标。2005年,Stark等人提出了形态成分分析(morphological component analysis,MCA)理论,该算法最开始应用于图像处理领域。通常将图像分解为纹理部分、卡通部分等,实现图像分离、修复、去噪、边缘检测等功能。随后,在盲源分离、雷达信号处理等方面也有广泛的应用。如文献[18]对海杂波和微动目标分别选取FT字典和QFM字典分离杂波和信号,得到微动目标的稀疏表示,大大提高了目标信号的能量聚集性。在文献[23]中,利用信号的共振特性,通过基于共振字典的MCA算法分离海杂波中的船只和鸟群回波。在文献[25]中,根据舰船尾迹和海面图像的奇异性差异建立相应的稀疏字典,通过MCA算法进行舰船尾迹检测。

本文对于同时包含海杂波和目标回波的雷达信号,根据形态成分分析方法,建立相应的时频域字典分离杂波和目标回波,并进一步提取目标的有效信息。

1 杂波和目标字典的选取

对于散射点目标,其回波可以表示为

()=(-)exp(j2π(-))

(1)

式中：()为雷达发射信号;为表示目标RCS特性的常数;为时延;为多普勒频率。

窄带雷达进行目标探测时,虽然其原始回波不具备稀疏性,但经过脉压后,其在距离维的分布可以视为是有限点组成的。当探测范围内的强散射点较少时,雷达目标回波可以看作一种稀疏信号。对于海杂波而言,海浪通常可以分为重力波和张力波,其中重力波占主导地位,而重力波可以用多分量单频信号进行表示,即使在高海况条件下,重力波的能量占比仍然很大。因此,在一定程度上海杂波也可以近似通过FT字典进行稀疏表示。根据文献[19],在时频域上,海杂波也可以进行稀疏表示。

最常见的时频分析方法是对信号作短时傅里叶变换(short time Fourier transform,STFT)。对于小目标而言,其雷达回波信号多普勒带宽相对较窄,因为其回波是由数量相对有限的长时间散射中心产生的。因此,通过时频分析,点目标的回波信号可以通过长窗长STFT字典或离散傅里叶变换字典进行稀疏表示。相比之下,由于海杂波是从经历复杂波动表面的后向散射回波的叠加,具有更广泛的时变谱,无法获得在某一时刻的精确模型。通过对海杂波的时频域特征进行分析可以看出,海杂波的多普勒带宽比目标宽得多,等效于瞬态信号,对时间分辨率的要求更高,用短窗长STFT字典可以获得比长窗长STFT字典更为稀疏的结果。

假设回波信号为(),其STFT可表示为

(,)=DFT{()(-)}

(2)

则STFT的逆变换为

(3)

式中：为频率索引;为滑窗重叠长度;=0,1,…,-1为滑窗序号。由此可以确定STFT字典为=[…-1],其中:

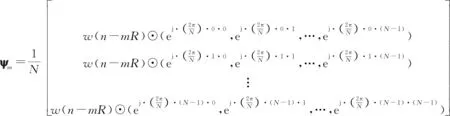
(4)

基于时频变换后得到的信号恢复原信号的一种方式是将每个滑窗截取的部分与滑窗相乘再求和,即:

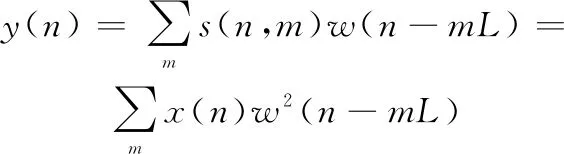
(5)

根据文献[28],选择半正弦窗口满足以上条件。半正弦窗表示如下:

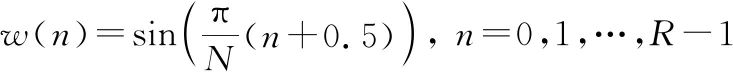
(6)

且据此生成的STFT字典满足=。因此,在本文中根据目标和杂波多普勒带宽的不同确定其对应字典分别为长窗长和短窗长STFT字典,且分析窗函数为半正弦窗以获得最优的重构效果。本文选取时频域STFT字典作为分离目标和杂波的基础,相较于文献[13]中采用的海杂波FT字典和微动目标QFM字典,包含了更多的时频域信息。

2 形态成分分析

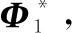
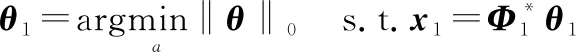
(7)

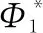
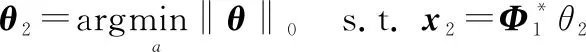
(8)

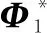
因此,在已知接收到的混合信号的条件下,可以通过求解如下目标函数来确定不同组成分量:

(9)

式中：=1-,0<,<1为正则化参数。MCA算法的核心即为在已知混合信号的条件下求解两个分量的稀疏系数向量,。常用求解方法多为基追踪算法(basic pursuit, BP)和正交匹配算法(orthogonal matching pursuit, OMP)的结合,如块坐标松弛(Block-Coordinate Relaxation, BCR)算法。本文根据文献[30]采用分裂增广拉格朗日乘子法对稀疏系数向量的、进行求解。该算法的核心思想是将一个大的最优化问题分解为几个更容易解决的子问题进行优化求解。具体求解过程如下。

首先,引入分裂变量:,,且=,=,则问题转化为

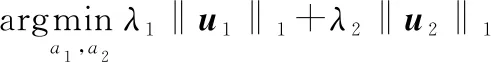
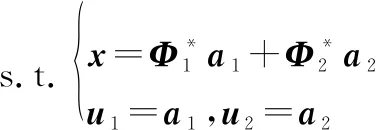
(10)

根据分裂增广拉格朗日乘子法,则该问题可分解为如下几个子问题:

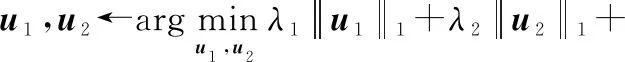
(11a)

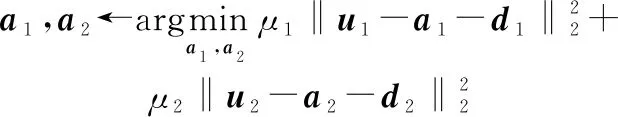
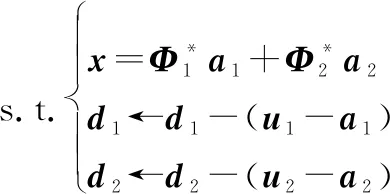
(11b)(11c)(11d)

式中：、是正标量,、的值不影响迭代的收敛性。

对于式(11a),显然,可以将、进行分开求解,即:

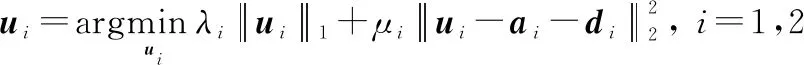
(12)

该函数可以通过软阈值函数求解,即:

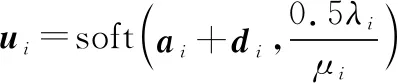
(13)

式中：soft(,)=max(0,1-||),为阈值,是一个正常数。当为向量时,其软阈值函数的解为按顺序求解每个元素的计算结果soft(,)。

对于式(11b),注意到函数:

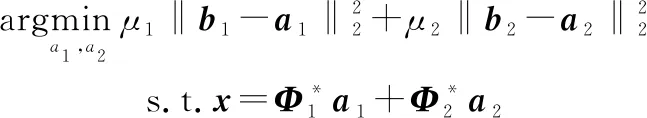
(14)

的解为

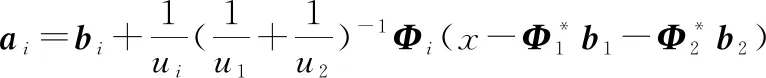
(15)

由此,代入=-,=1,2可以求得稀疏系数向量、。

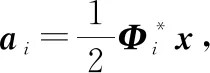
3 目标提取算法设计

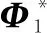
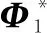
初始化=0,=0,和最高迭代次数iterMax;

计算向量=soft(+,05)-;

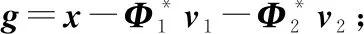
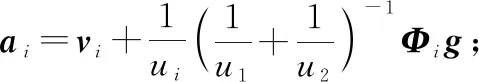
更新误差向量:=-;

如果迭代次数、;

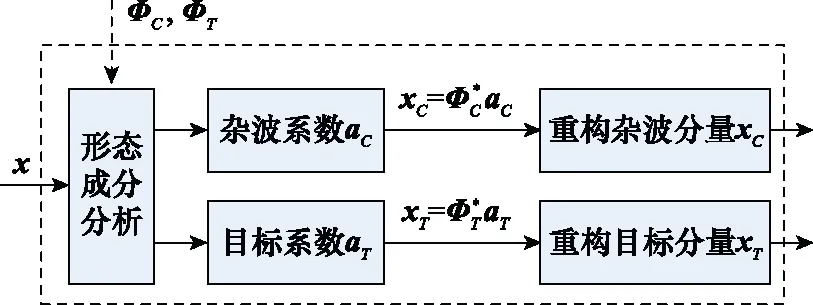
图1 分离杂波和目标回波的算法流程图Fig.1 Flow chart for separating clutter and target echo

4 实验验证

选取C波段某型号雷达对某海域的探测数据,环境条件为北风6～7级,浪高约2 m,阵风8级,在25 km内杂波强度较大,目标回波非常微弱,对原始回波进行脉冲压缩处理后也无法直接获得目标信息。

4.1 使用STFT字典重构杂波的可行性

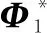
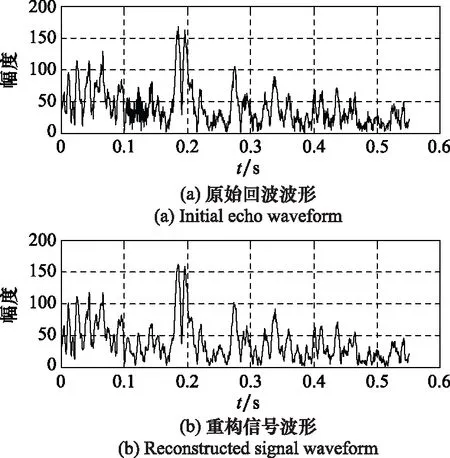
图2 原始回波和重构信号的时域波形Fig.2 Initial echo and reconstructed signal waveform

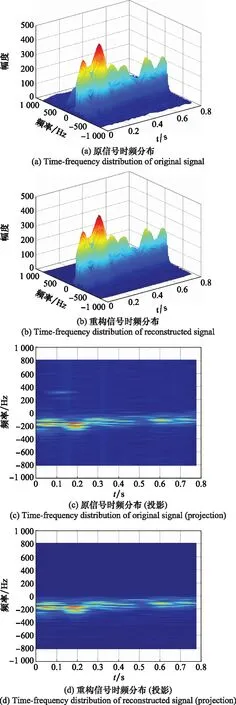
图3 接收回波和重构信号的时频域分布Fig.3 Time-frequency distribution of original echo and reconstructed signal

定义重构的相对均方误差为

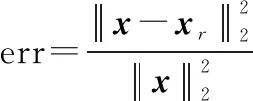
(16)

式中：为实际接收到的杂波信号;为根据杂波字典重构的信号。当稀疏系数向量中非零元素个数分别为100、200、300、400、500、550、600时,重构误差如图4所示。记非零元素个数为,的大小反映了重构信号中包含的主要成分数量的多少。当较小时,由于包含分量较少,重构误差较大;在一定范围内,随着的增大,包含的主要分量增加,重构误差会有所减小;但进一步增大时,不仅增加了计算量,选取的原子之间可能会相互影响,增加了冗余信息,导致信号的重构误差增大。

图4 非零元素个数对重构误差的影响Fig.4 Influence of non-zero elements’ number on reconstruction error

由于海杂波是复杂波动表面的散射回波的叠加,在时域上变化较大,更等效于瞬态信号,因此,当杂波STFT字典的滑窗长度增加时,重构误差增大,如图5所示,并且会对时域分辨率造成一定损失。

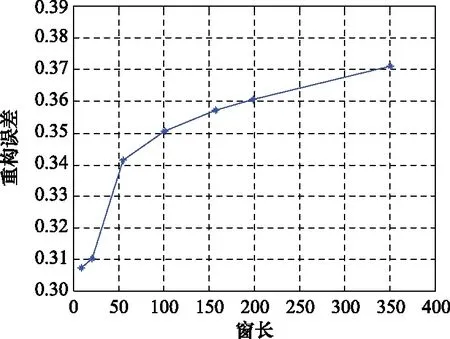
图5 字典窗长对重构误差的影响Fig.5 Influence of dictionary window-length on reconstruction error

4.2 形态成分分析分离杂波和目标回波

现以第137距离门内回波脉压信号为例,按第3节所示步骤进行处理。此时回波中主要包含两部分信息,即杂波信号和目标信号的叠加,且杂波强度较大。因此,选取不同窗长的STFT字典根据第2节所述算法对回波进行处理。其中,杂波字典窗长=9,目标字典窗长=550,相邻两滑窗之间的重叠区域为50%。当目标字典窗长不够长时,目标重构结果往往会混入一部分杂波信号,对杂波和目标信号的分离结果产生较大影响。从脉压后数据的时域和频域波形图中可以看出,目标淹没在杂波中无法检测。通过MCA处理后,分别获得稀疏重构后的杂波分量和目标分量,如图6、图7所示。虽然杂波部分占据了回波的大部分能量,但通过对目标部分进行处理,可以清晰地获得目标信号的时域、频域和时频域的具体信息,分离效果显著。

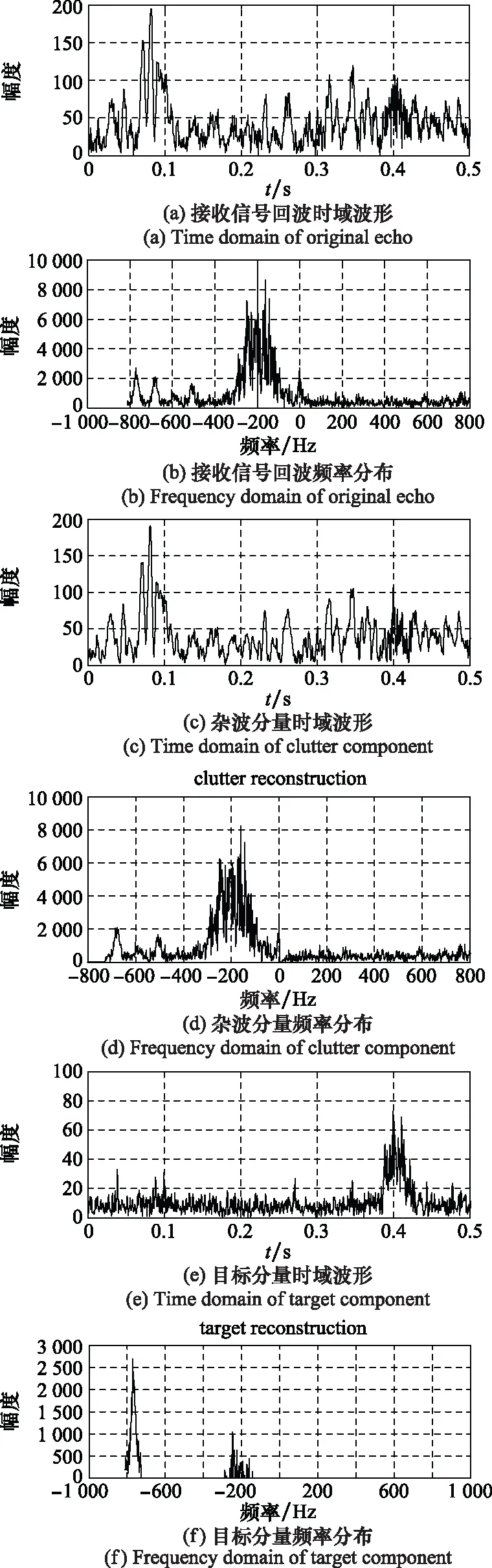
图6 MCA后各分量的时频域波形Fig.6 Time and frequency domain of each component after MCA

在该距离门内不存在目标的情况下,使用2个字典和MCA算法对输入信号进行分解,得到目标分量的时域波形如图8所示,该分量内没有明显的目标,与图6(c)对比,可以通过设置一定的门限判断该距离门内目标是否存在。

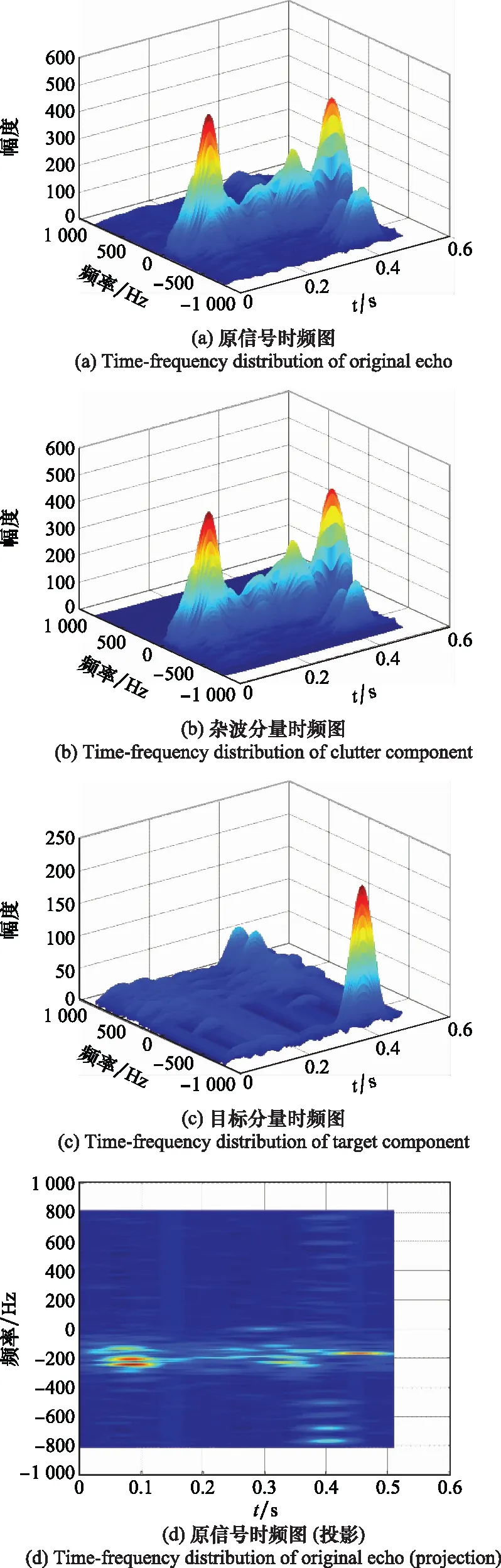
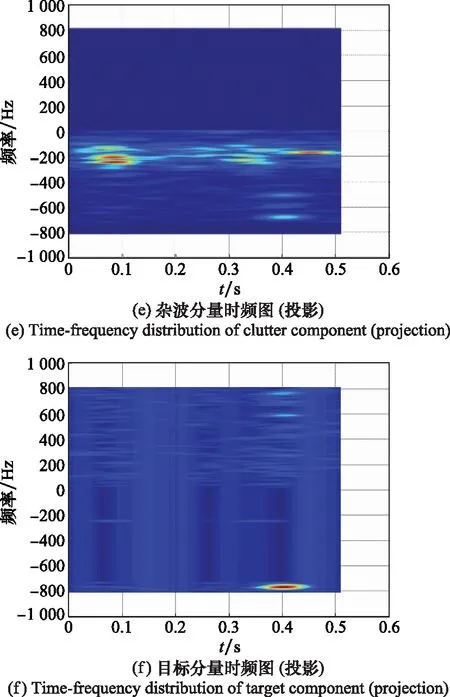
图7 MCA后各分量的时频域分布Fig.7 Time-frequency distribution of each component after MCA

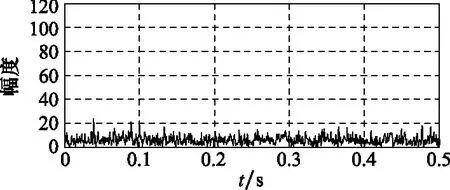
图8 无目标时目标分量时域波形Fig.8 Time domain of target component when no target signal input

在海杂波强度较大的背景下,由于海杂波的运动特性,杂波会有一定的多普勒频域范围。当运动目标径向速度较慢时,目标的多普勒频率处于杂波的频谱范围内,由于传统的MTI、MTD技术仅通过目标和杂波多普勒频率的不同进行检测,在这种情况下,传统算法就会失效,无法从杂波中准确检测目标。而MCA算法是通过时频域字典区分杂波和目标回波的,在无法仅通过多普勒频率检测目标时仍可以有效分离杂波和目标信号,并通过对目标分量进行处理获得目标的有效信息,如图9所示。

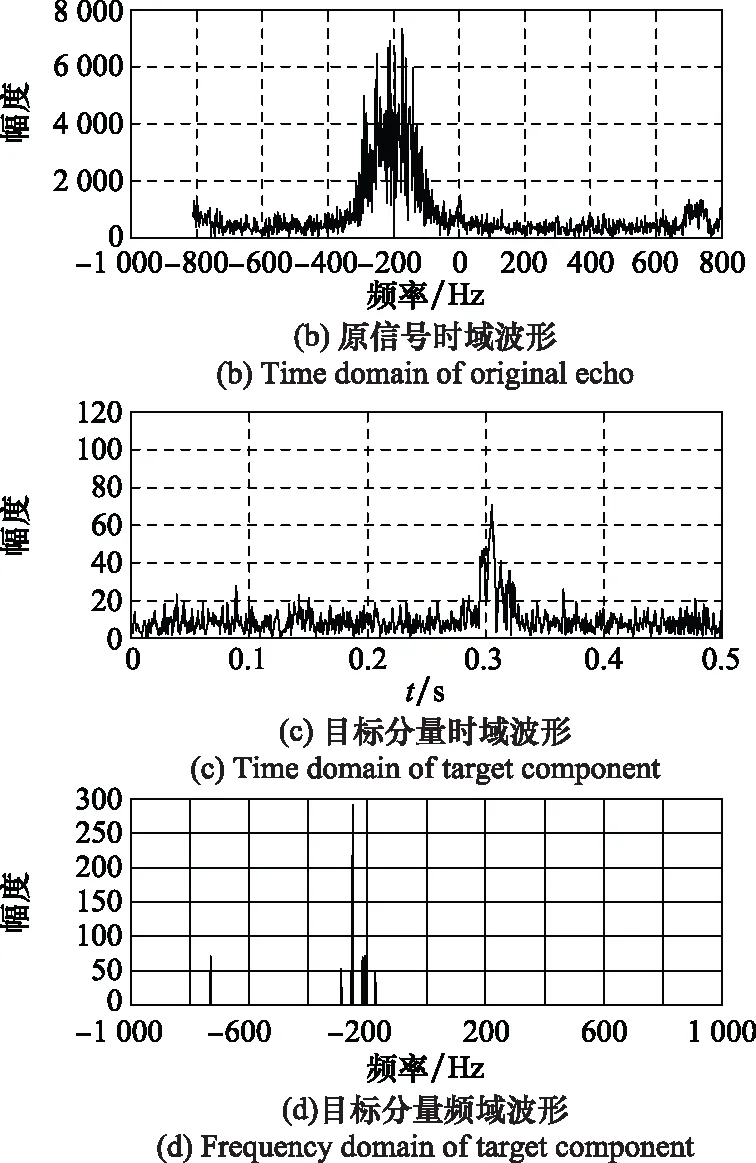
图9 一慢速目标通过MCA分离后时域、频域分布Fig.9 Each component of time and frequency distribution of a slow target after MCA

4.3 算法参数选择

(1)字典窗长的确定

固定迭代次数为50次,设置参数为=005,==2。考虑字典窗长、对结果的影响。

当固定杂波字典窗长=9,改变目标字典窗长时,以目标分量的时域波形图作为示意,结果如图10所示。当目标字典窗长较小时,目标分量中会混入较多的杂波信号,甚至存在杂波幅度高于目标的情况,无法直接从目标分量中获取目标信息;进一步加大目标字典窗长,使之与杂波的区分度增加,增强了杂波抑制能力。

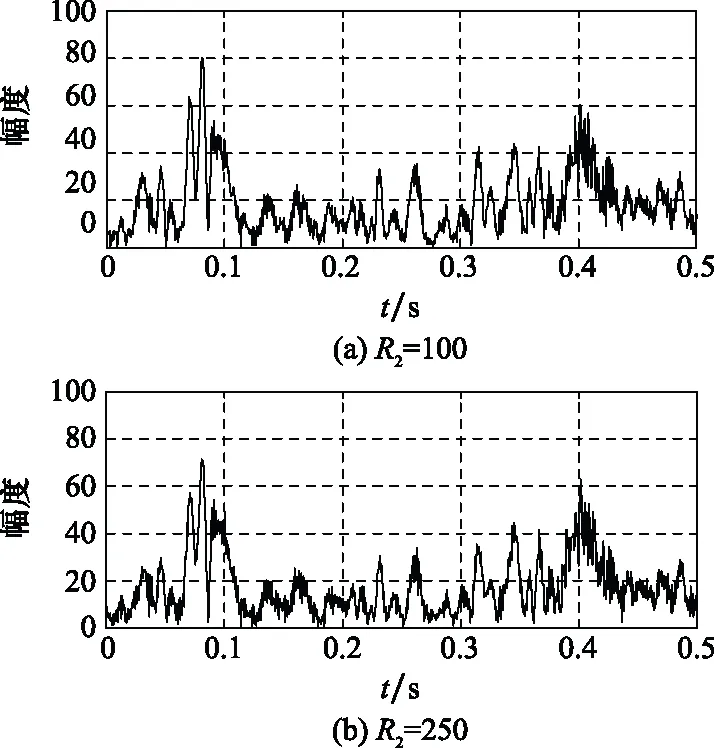
图10 目标字典窗长对杂波抑制性能的影响Fig.10 Influence of target dictionary window length on clutter suppression performance

当固定目标字典窗长=550,改变杂波字典窗长时,以目标分量的时域波形图作为示意,结果如图11所示。当杂波字典窗长较大时,目标分量中目标信号与杂波区分度不高,容易被短时的强杂波所干扰,无法有效地凸显目标信息;减小杂波字典窗长,使之与目标的区分度增加,可以有效提取目标信息。

对于形态成分分析而言,本文根据目标和杂波多普勒带宽的不同,采用不同窗长的时频域字典对接收信号进行分离,窗长是区分杂波和目标的重要参数。因此,在杂波使用短窗长STFT字典、目标使用长窗长STFT字典的前提下,需要使杂波和目标在窗长上的区别度尽可能大,才能有效地进行杂波抑制,提取目标信号。

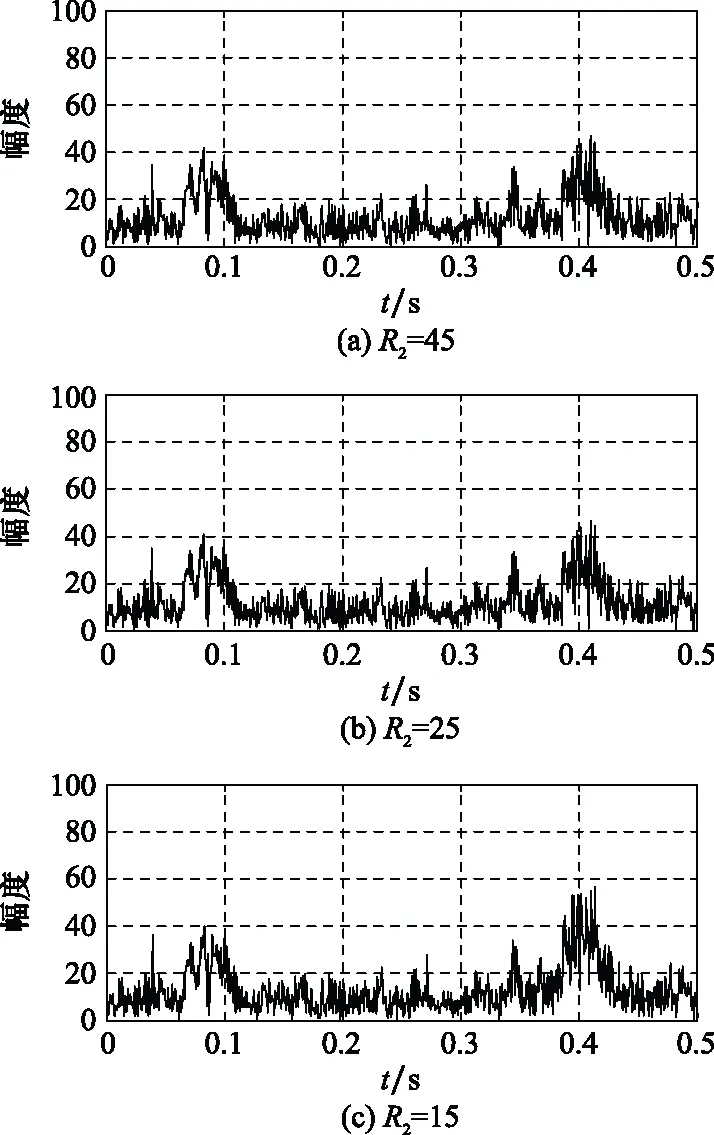
图11 杂波字典窗长对杂波抑制性能的影响Fig.11 Influence of clutter dictionary window length on clutter suppression performance

(2) 迭代次数

在MCA处理中,通过将较大的问题分解为多个子问题进行迭代求解以得到最终结果。随着迭代次数的增加,求得的目标部分中的杂波剩余不断减少,目标分量中的信杂比有所提升。当迭代次数的增至500次以上时,目标分量中的信杂比增速放缓,信杂比趋于稳定。

与传统的动目标显示(moving target indicator, MTI)算法相比,接收信号经过MTI处理后输出信杂比约为15.324 4 dB而MCA算法仅通过少量迭代就可以达到该输出信噪比,增加迭代次数,可以进一步提高输出信杂比,如图12所示。

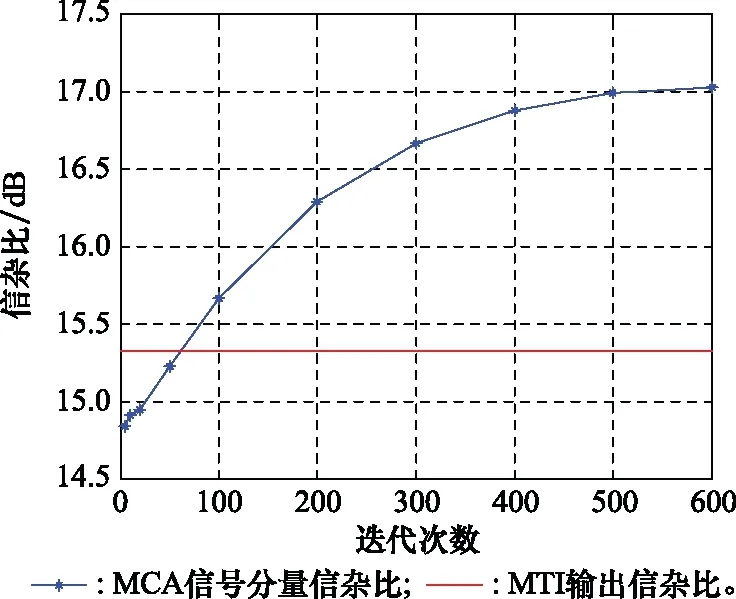
图12 迭代次数对目标分量信杂比的影响Fig.12 Target component SCR change on iteration number

同时,如图13所示,信号经过MTI处理后在0.08 s处仍存在一些强度较大的杂波,而MCA算法可以将此处杂波有效抑制,因此,MCA算法对一些干扰性较强的短时杂波抑制效果更好。并且在频域上,MTI处理后仍存在较多杂波频率,而通过MCA算法处理后可以获得较准确的目标频率信息。综合来看,MCA算法性能优于传统杂波抑制算法。

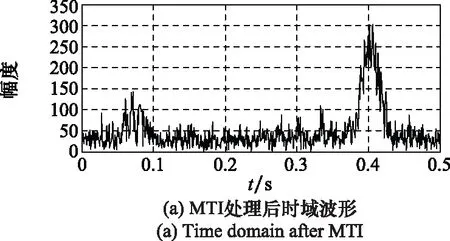
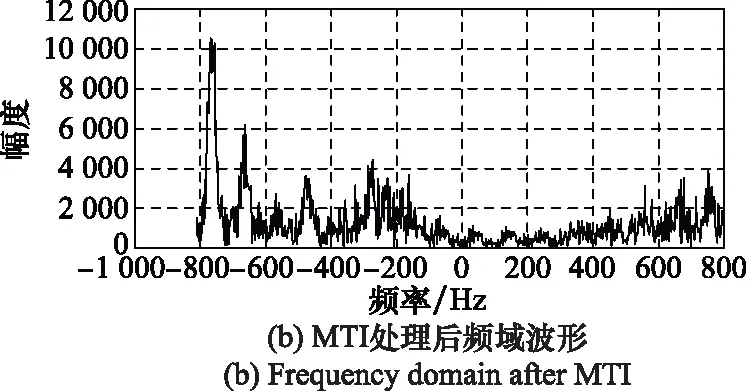
图13 MTI处理后的时频域波形Fig.13 Time and frequency domain after MTI

5 结 论

对于海杂波中的目标探测问题,本文在稀疏分解理论的基础上,依据杂波和目标信号在多普勒频率分布特征上的区别,分别建立不同窗长的时频域字典,并通过基于分裂增广拉格朗日算法的形态成分分析迭代求解相应的稀疏分解系数向量,再将字典和对应系数向量相乘重构出杂波分量和目标分量,实现杂波和目标的分离。对重构的目标分量进行处理,可以提取目标特征。通过实测数据验证了该算法的有效性,并分析了参数对分离效果的影响。与传统MTI算法相比,该算法的杂波抑制效果更好,并且能够提高目标信号的能量聚集性。