辐射式仿真中PCM信号间歇收发回波重构方法

谢艾伦, 刘晓斌, 赵 锋, 艾小锋, 肖顺平

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

通过对真实目标进行外场试验来获取目标的特征,评估雷达性能往往是一项高成本、高复杂度、长耗时的任务。而在微波暗室里面进行雷达辐射式仿真可以显著地减少成本、缩短试验周期、降低试验开展的难度。但雷达信号的脉冲时长对应的传播距离远大于微波暗室尺寸,带来发射信号与目标回波互耦的问题,严重制约了微波暗室仿真试验的开展。近年来,结合间歇采样的思想把脉冲信号分成多个短脉冲进行间歇收发,能够有效解决收发信号互耦问题。

目前利用间歇收发开展暗室目标测量仿真的研究主要集中于线性调频信号回波特性及重构方法。文献[4]分析归纳了辐射式半实物仿真中雷达脉冲等效测量面临的瓶颈问题,并提出用间歇收发解决暗室仿真中的互耦问题。文献[5]针对线性调频信号,提出了微波暗室中脉冲雷达进动目标微动特征的提取方法。文献[6]提出了线性调频信号经间歇收发后的高分辨距离像(high range resolution profile,HRRP)重构方法。相比之下,脉冲编码调制(pulse code modulation,PCM)信号在微波暗室中的目标测量方法未见报道。文献[8-10]表明,PCM信号在抗干扰性能方面优于线性调频信号,在暗室中采用PCM信号进行目标探测对于外场试验具有指导意义。但是,在暗室中对PCM信号间歇收发带来的信号缺失,将导致脉冲压缩后距离像旁瓣的升高,从而影响目标的分辨能力。因此,研究回波重构方法十分重要。目前针对线性调频信号的回波重构方法有基于时频特性的重构方法,基于Dechirp过程的重构方法,这些方法均不适用于PCM信号。因此,本文提出了基于匹配滤波变换基的回波重构方法,实现对间歇收发PCM信号回波的精确重构。

本文基于间歇采样的思想,通过对PCM信号进行间歇采样,分段收发,解决暗室仿真的互耦问题。首先分析了PCM信号间歇收发前后的匹配滤波输出特性;接着结合压缩感知理论,针对PCM信号提出了基于匹配滤波变换基的回波重构方法,对回波进行精确重构,解决间歇收发带来的距离像误差大的问题,并给出暗室仿真中具体的间歇收发处理方法。最后结合计算机仿真,验证了该方法的有效性和可行性。

1 PCM信号间歇收发处理方法

1.1 间歇收发流程

间歇收发的处理过程如图1所示,即通过不断切换收发开关,把原本完整的信号分段,交替收发,不断重复此过程。每一小段脉冲可以达到亚微秒量级甚至更短,有效解决暗室仿真中的收发互耦问题。

图1 间歇收发示意图Fig.1 Schematic diagram of Intermittent transmitting and receiving

为便于分析,把间歇收发过程抽象为一个间歇收发控制信号,如图2所示。间歇收发控制信号是一个周期脉冲串,用()表示该信号,设其脉宽为,重复周期为。其表达式为

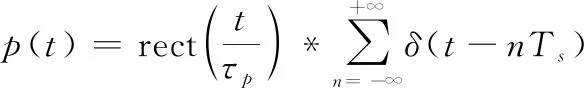
(1)

式中:*表示卷积运算;()是冲激函数。对雷达信号进行间歇收发等效于用雷达信号与()做乘积。

图2 间歇收发控制信号Fig.2 Intermittent transmitting and receiving control signal

1.2 完整PCM信号匹配滤波输出

设PCM信号复包络为(),具体表达式为

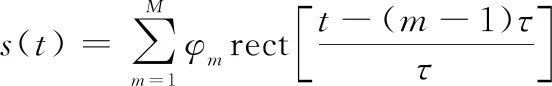
(2)

式中:为第个编码的编码值,取-1或1,改变其排列方式和个数就可以表示不同的编码序列;为码元个数;为一个码元的宽度;总信号时长为。式(2)就是二相编码信号的时域表达式。

设匹配滤波器单位冲激响应为(),表达式为

()=(-)

(3)

式中:表示常系数；(·)表示取共轭;为白噪声中匹配滤波输出信噪比最大的时刻,一般选择=。

设信号经匹配滤波器的响应为(),其与()和()的关系为

()=()*()=()*(-), 0≤≤

(4)

由文献[17]可知,式(4)结果为

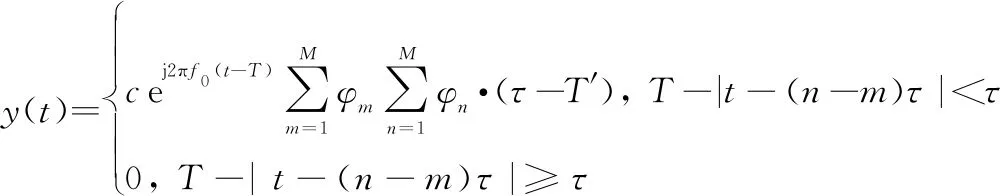
(5)

式中:′=|--(-)|。式(5)就是PCM信号进行匹配滤波输出的具体表达式。

1.3 间歇收发PCM信号匹配滤波输出

式(1)构建的间歇收发控制信号()与PCM信号()进行乘积运算,可以得到间歇收发后的PCM信号′():

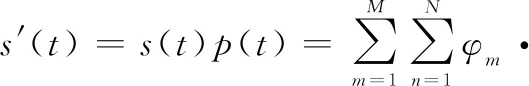
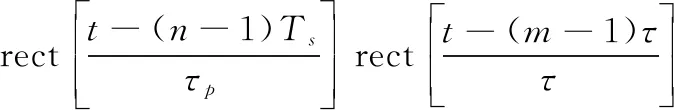
(6)

在发射PCM信号时,一般设定较小的码元宽度以获得高的距离分辨率,因此通常有大于,为简化推导,可以假定收发参数正好是码元宽度的整数倍,即=,=,其中和为正整数,从而对式(6)进行简化:

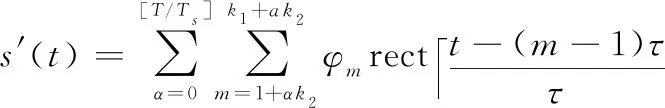
(7)

设′()的匹配滤波输出为′(),′()具体结果如下:

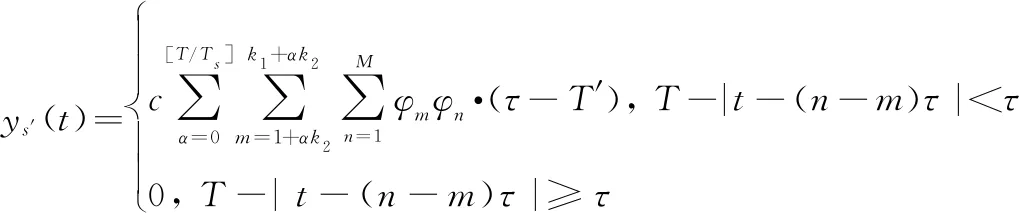
(8)

间歇收发回波距离像的误差来源于峰值误差和散射点中心位置的误差。其中,式(5)与式(8)给出了峰值误差大的理论解释。回波距离像的误差会影响目标信息测量的精度,影响目标的分辨与成像。本文结合压缩感知原理对间歇收发回波进行精确重构以解决该问题。

2 基于匹配滤波变换基的重构方法

2.1 压缩感知原理

压缩感知的主要思想可以表述为:一个能够被稀疏分解的信号,在满足不相关性的观测矩阵测量后,可以得到一个测量向量。然后通过选择合适算法对测量结果求解优化问题,就可以求出原信号。

(9)

通过求解凸优化问题可以求解出:

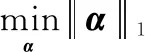
(10)

2.2 构造间歇收发观测矩阵

对信号的间歇收发可等效看作是用相应的观测矩阵对信号的时域进行观测。对间歇收发控制信号进行对角化处理,在每个对应脉宽内赋值为1,其他地方赋值为0,可以得到观测矩阵。

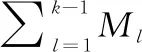
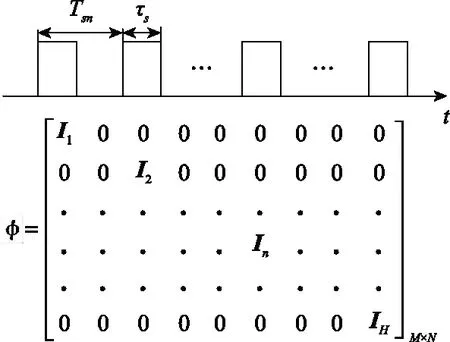
图3 间歇收发观测矩阵φ构造原理图Fig.3 Schematic diagram of the construction of intermittent transmitting and receiving observation matrix φ

在图3中,表示×的单位矩阵,并且满足∑=,∑=。

2.3 构造匹配滤波变换基

能够找到一个变换基对信号进行稀疏分解,是运用压缩感知理论需要满足的一个前提条件。选取的稀疏变换基应该使得信号拥有良好的稀疏分解结果,即大部分元素为零,只有极少的非零元素。这样可以提升重构速率和重构精度。

受启发于PCM信号匹配滤波输出为较高的主峰和较低的杂乱旁瓣,并且主峰幅度比旁瓣大得多这个特性,本文针对PCM信号构造了匹配滤波变换基。其构造过程如下。

假设不经过间歇采样发射的完整PCM回波信号为(),参考信号为(),且有()=(),()为待发射的PCM信号。设()为匹配滤波输出结果。则根据匹配滤波关系有

(11)

根据傅里叶性质,式(11)变换为

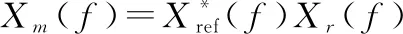
(12)

式中:()是()的频谱;()是()的频谱;()是()的频谱。

由式(12),对于信号进行采样得到离散矩阵,每个采样点都满足

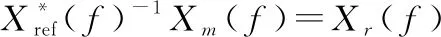
(13)

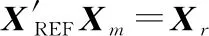
(14)

式中:表示傅里叶变换矩阵;表示傅里叶逆变换矩阵。对两边同时乘以进行傅里叶逆变换,得到

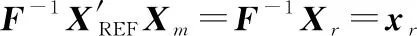
(15)

是第22节构造的间歇收发观测矩阵,形式见图3,设为回波经过观测得到的结果,即是间歇收发回波,满足

=

(16)

把式(15)代入式(16)可以得到

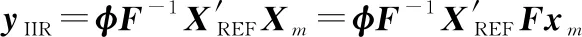
(17)

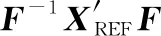
(18)

(19)

2.4 重构流程

综合上文,完整的重构流程如图4所示。

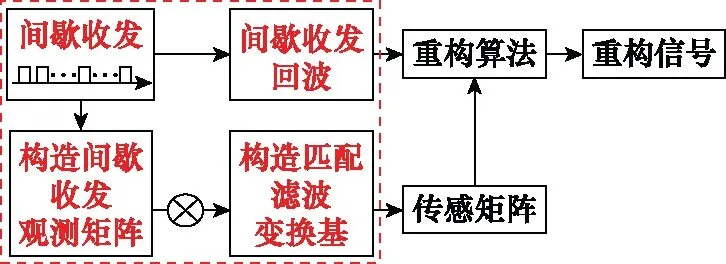
图4 重构流程图Fig.4 Reconstruction flow chart

实现信号重构的3个核心步骤如下:

对PCM信号进行间歇收发得到间歇收发回波,同时根据间歇收发参数构造出等效的间歇收发观测矩阵。

利用匹配滤波变换基对信号进行稀疏分解,并与间歇收发观测矩阵相乘得到传感矩阵。

选择合适的算法从观测值中求解信号。

本文采用的重构算法是正交匹配追踪(orthogonal mat-ching pursuit, OMP)算法。

3 仿真分析

本文结合间歇采样思想和压缩感知理论,分析了PCM信号在暗室测量的具体方法,并提出了回波重构方法。为验证其正确性,采用计算机仿真进行验证。考虑一个3散射点目标模型,实验参数如表1所示。采用此参数进行PCM信号的间歇收发与回波重构,对其进行分析,仿真结果如图5所示。

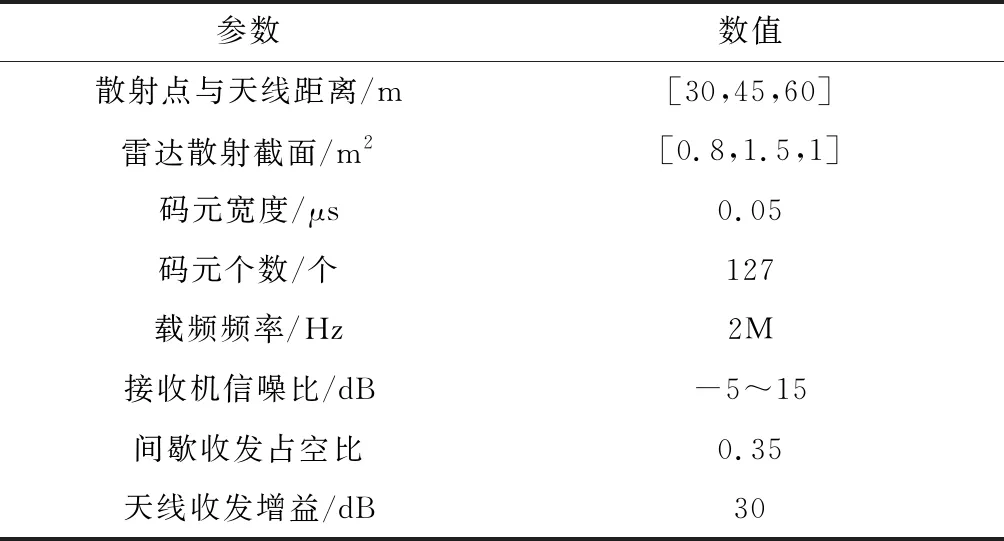
表1 实验参数列表

图5(a)是3个散射点目标回波重构的距离像。间歇收发回波距离像3个峰值在30 m,45 m,75 m处,第3个散射点峰值位置与理想存在较大偏差,且距离像旁瓣较高,幅度接近主瓣,距离像存在严重误差。对回波进行压缩重构后,重构回波距离像恢复到与完整回波距离像一致。图5(b),图5(c)和图5(d)是第一个散射点间歇收发回波重构前后的幅度、位置与相位测量信息。低信噪比时,重构回波测量信息与完整回波测量信息有所偏差,随着信噪比升高,测量信息逐渐趋于一致,验证了压缩感知重构方法能够有效恢复间歇收发回波的信息。

图5 间歇收发回波重构结果Fig.5 Results of intermittent transceiver echo reconstruction

重构信息与原始信息残差小于一定的值,则可以认为重构成功。在距离像中,当重构峰值位置与理想值残差小于距离分辨单元,且所有散射点归一化峰值幅度差均小于幅度偏差门限γ,可认为重构成功,仿真中取0.1。本文研究了基于匹配滤波基的回波重构成功率与信噪比、间歇收发周期的关系,图6为仿真结果。

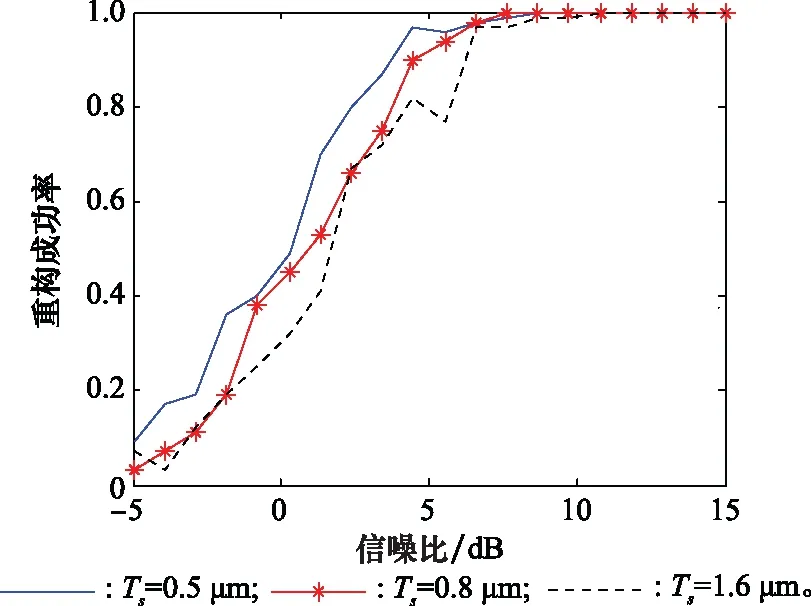
图6 重构成功率Fig.6 Success rate of reconstruction

重构成功率随着信噪比的增大而显著增大,在信噪比为-5 dB时重构成功率不超过10%,但当信噪比达到10 dB后,重构成功率达到95%以上。对比不同曲线,在信噪比一定时,间歇收发周期越小,则重构成功率越大,原因是低的间歇收发周期对PCM信号的采样更加均匀,其距离像峰旁瓣幅度相对下降,改善了距离像重构性能。

4 结 论

本文结合间歇采样思想和压缩感知重构理论,给出了PCM信号应用于微波暗室测量的具体方法,即对PCM信号进行间歇收发,再根据压缩感知理论对回波进行精确重构。因此,本文分析了间歇收发后PCM信号经过匹配滤波器的输出。为解决间歇收发带来的距离像误差,本文结合压缩感知理论,提出了基于匹配滤波变换基的回波重构方法,并通过仿真验证了本文所提重构方法的有效性。本文方法对于暗室仿真具有借鉴意义。