深海采矿柔性立管系统非线性有限元模拟

佟 莹， 夏 健

(南京航空航天大学 航空学院，南京 210016)

1 引 言

管道提升式深海采矿系统以其采集效率和技术可行性等优势成为最具发展前景的深海采矿模式。为适应复杂的深海采矿环境，需采取稳定性好和环境适应性强的管道提升系统。全柔性立管系统[1,2]无需多级泵组推送，结构精简，系统灵活性高，大长度海洋柔性管道对复杂海底环境适应性强，采矿作业范围广，且柔性管路材料的耐腐蚀性和柔韧性有助于提升采矿系统使用寿命，具有广阔的工程应用前景[3]。但全柔性管道提升式深海采矿系统发展时间较短，其理论研究还不成熟。

目前，对于结构大变形及其非线性特性的研究广泛采用有限单元方法。肖林京等[4]采用T.L.列式法描述深海扬矿钢管系统的力系平衡，建立几何非线性有限元基本方程，通过采矿船加速、匀速和减速拖航时扬矿管的偏移构型、横向速度、加速度及弯曲应力等参数表征其动力学响应和非线性动态特性。郭小刚等[5]基于悬链线理论对深海扬矿钢管系统底部软管段进行了非线性静平衡分析。Garcia-Palacios等[6]采用U.L.列式法描述力系平衡并建立非线性有限元基本方程，基于ANSYS软件框架编写结构模型的数值计算程序，对聚乙烯管的布放入水过程进行了几何非线性动力学分析。马今伟等[7]采用U.L.列式法基于非线性无额外自由度广义有限元法对弹塑性大变形静力学问题进行了非线性分析。樊玉新等[8]使用张量体系描述的非线性有限元模型分析柔性体大变形过程。与传统有限元方法相比，基于连续介质力学思想，张量体系描述的非线性有限元模型的模化和计算过程更加精简，更便于代码开发。张量体系描述的随体坐标与等参单元的自然坐标之间的一致性在连续介质和有限单元模型之间建立了光滑过渡。此外，克服了结构运动小变形假设关于位移和变形的约束，适应性更广。

基于三维固体有限变形理论[9]，本文采用张量体系描述结构运动和力系平衡，建立全柔性立管系统的数学模型，推导了系统运动控制方程，针对几何非线性和非保守载荷等关键问题提出了有效处理方案。采用非线性有限元法处理计算模型，通过工程算例的模拟结果验证理论方法和计算模型的有效性和实用性。

2 物理模型

柔性立管系统将海面上静止的能量供应母站与海底自推进集矿系统直接联接，通过单级泵经柔性立管将矿浆泵送至水面，依靠灵活柔性管道适应海底复杂作业环境，原理如图1所示。管道大变形属几何非线性问题，海洋环境载荷随管道构型变化而变具有非保守力属性，耦合双重非线性特征成为发展数学模型的关键问题。

3 数学模型

本文从连续介质力学有限变形理论出发，建立张量体系描述的非线性有限元模型。将柔性管道简化为索单元，管路位形由其轴线位置描述，采用T.L.列式法，取t=0时刻无应变和位形已知的初始构型C0为参考构型，结构运动和力系虚功(惯性力、内力和外力)均相对于C0定义。取能量共轭的第二类Piola-Kirchhoff应力张量和Green应变张量度量结构应力和应变，由达朗贝尔原理[10]建立连续系统动力学平衡方程，

(1)

式中L0和A0分别为C0索单元的初始长度和截面面积。基于式(1)，柔性管道运动的位移和应变不受小变形假设约束。

图1 柔性管道提升式采矿系统原理

采用随体坐标ξi描述管道大变形，初始时刻长度为ds0的线元dr=gidξi，当前构型C变形后线元dR=Gidξi的长度为ds。gi和Gi为材料点ξi在C0和C的协变基矢量，为空间点位的函数。张量体系中Green应变张量E可由线元的长度变化定义，

(2)

式中g11和G11为C0和C的度量张量的协变分量，g11=g1·g1，G11=G1·G1。E11为位移的非线性函数。

第二类Piola-Kirchhoff应力张量S的逆变分量为

S11=Eg11g11E11

(3)

式中E为弹性模量，g11为C0度量张量的逆变分量，g11g11=1。同理，S11为位移的非线性函数。

作用于大变形柔性管道的海洋环境载荷具有非保守力属性。将C中随时间变化的线元AdL矢量映射至C0得与时间无关的edL0，取T为流体面力矢量，则有

(4)

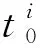
将有限元列式的单元平衡方程匹配至全局[12]得矩阵形式的系统运动微分方程，

(5)

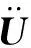
4 计算模型

4.1 非线性静力学方程求解

非线性静力学方程为内力与外力间的平衡，外力作用下张紧管线获取抵抗外力的结构刚度。内力向量R为节点位移向量U的非线性函数[8]，对R进行Taylor序列展开至线性项，定义非线性的切线刚度矩阵K，

Rn + 1=Rn+[Kn] ΔUn + 1

(6)

由逐步加载与Newton-Raphson迭代混合的数值求解方法抑制非线性方程的数值解漂移及迭代计算不收敛等问题。混合法保证每次增量加载引起的位形变化满足特定误差精度，且能有效抑制纯增量加载的误差累计。采用粘性松弛技术[9]引入人工阻尼D，以保证初始无应变状态下刚度矩阵K非奇异。第k+1个增量载荷作用下，第n+1次迭代，系统的静力学平衡方程为

(7)

为加速收敛，人工阻尼矩阵D随增量推进满足如下关系，

(8)

[D]=μk + 1[D]

(9)

式中μ为阻尼因子，γ为衰减因子。阻尼因子μ随着载荷增量推进而变化。衰减因子作为粘性松弛技术的控制参数，可视求解问题而定。本文静力学分析算例中，初始阻尼因子为0.01，衰减因子为0.1，初始阻尼元素初值为 1.0e +4。

4.2 非线性动力学方程求解

为有效求解系统非线性动力学响应，本文采用广义α隐式时间推进格式[10]，综合了Newmark法、HHT-α法和WBZ-α法的特征，通过调整数值参数保证高频段具备高速衰减的数值阻尼过滤虚假高阶振型，而在低频段控制较小的数值阻尼保证数值解的精度。基于广义α格式，t+Δt时刻节点的速度和位移满足如下关系,

(10)

式中数值参数γ和β满足关系(11，12)时，算法无条件稳定且具备二阶精度,

(11,12)

αm和αf为插值系数，经t和t+Δt时刻参量插值，t+Δt时刻节点的运动学参量及外载修正如下,

Ut + Δ t=(1-αf)Ut + Δ t+αfUt

Ft + Δ t=(1-αf)Ft + Δ t+αfFt

(13)

直接积分法通过构造t+Δt时刻位移与t时刻已知变量的递推表达式完成时间推进。由式(13)可推导得系统等效线性方程组

[Keff] ΔU=Feff

(14)

式中

本文采用Rayleigh阻尼矩阵C将实际结构阻尼矩阵简化为质量矩阵M和刚度矩阵K的线性组合，系数cM和cK由实验给出,

C=cMM+cKK

(15)

本文取cM和cK均为5.0e -4。

5 非线性有限元程序验证

基于上述计算模型，采用FORTRAN语言编写非线性有限元数值计算程序。目前，认为Verification & Validation[13]是评估非线性问题数值计算模拟可靠性的最客观方式，其验证过程如图2所示。

图2 模型验证和确认的工作范围

为了验证本文方法处理几何非线性问题的有效性，采用网格收敛指数(GCI)方法[14]客观评定渐近解的离散误差范围。初始长度L=0.35 m，线密度ρA=0.314 kg/m，重力加速度g=2.0 m/s2，弹性模量E=1.4e+6 Pa的均质链条自0.1π位置释放的自重驱动悬挂链条摆动，时间步长为 5.0e -3 s。图3展示了基于三组网格密度(10 elems，20 elems，40 elems)，不同时刻满足收敛标准的数值模拟结果及自由端位移和速度的GCI指数。数值结果表明，40 elems网格密度下，本文计算模型对几何非线性问题具有稳定的预测能力。速度场渐近解的离散误差范围大于位移场，但收敛指数仍在置信范围内，说明计算模型能够有效处理数学模型的非线性动力学特征。

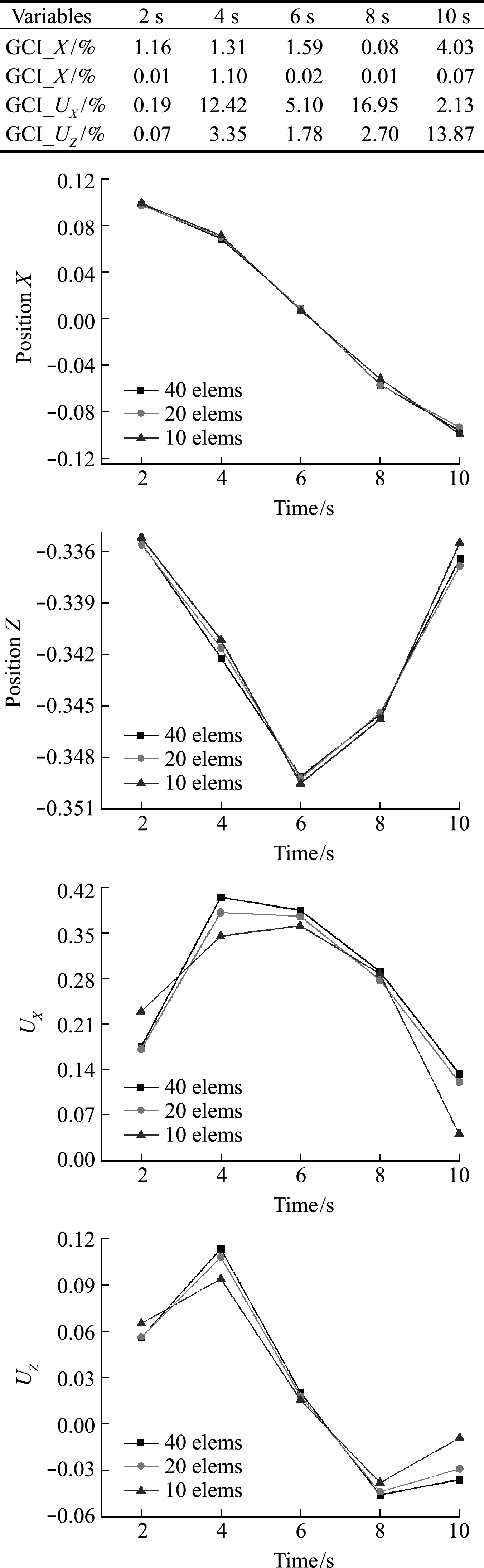
图3 计算模型验证

取该算例的实验与解析解[15]及现有数值模拟结果[16]为参考，验证本文方法计算结果的准确性。图4为自释放起2.4 s内链条构型随时间变化历程，右侧自由端的踢腿现象与实验观察结果一致，说明张量体系描述的非线性有限元法成功反映了张紧力为结构运动提供刚度的真实物理现象。此外，相比于常规有限元法忽略刚度引起抖动的踢腿，本文数值结果更加光滑，说明本文计算模型能够有效处理速度梯度过大引发数值计算不稳定的问题。由10次往复摆动历程数值结果计算平均周期(T=2.196 s)和特征参数gT2/L=27.556(由解析解计算其理论值为27.3[14])。数值结果与理论解的一致性验证了本文计算模型的准确性和有效性。

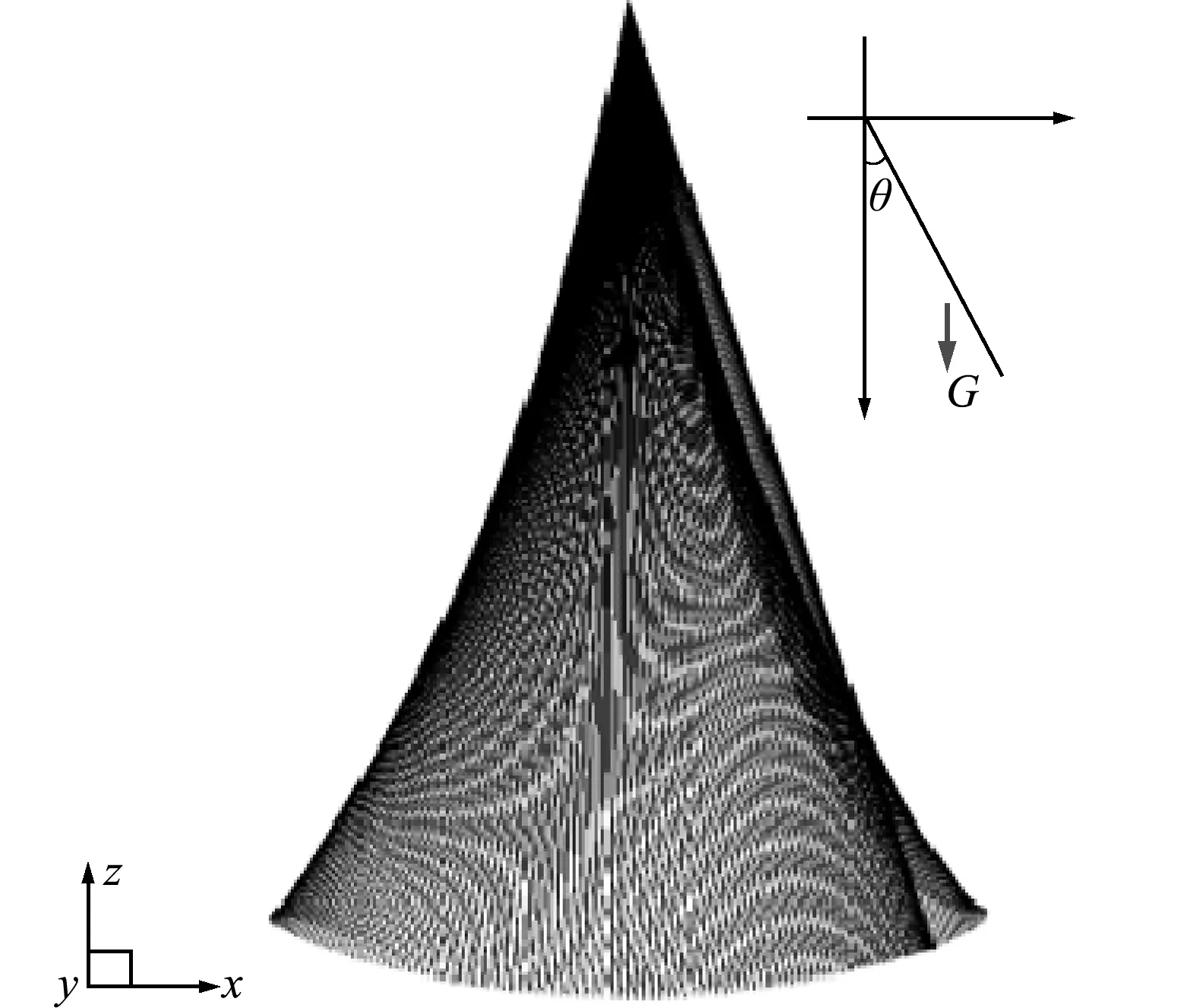
图4 自重驱动锁链构型变化时间历程

6 柔性管道非线性特性分析

以完成410 m浅水水试的全柔性立管系统[1]为例，采用本文数值计算程序分两阶段对柔性管路非线性响应特性进行分析。柔性管路长500 m，内外径为0.4445 m和0.508 m，弹性模量为1.4 GPa，单位长度管线湿重为3336.9 N/m，扬矿矿浆混合液密度为1130 kg/m3，海水密度为1030 kg/m3。自尾端10 m位置起装有80 m范围的浮力装置，结构如图1 所示。离散有限单元模型由100个等参索单元构成，水面母站联接Node 1，集矿机联接Node 101。

6.1 柔性管道非线性静力学分析

第一阶段为柔性立管系统稳定作业状态的静力学分析。图5为水面母站静止，集矿机与母站之间水平距离X=40 m，80 m，120 m，160 m，200 m和240 m时，柔性立管系统的静平衡构型。X较小时，浮力块作用下海底管路呈S型剖面，该模拟结果与水试实验结果一致[1]。随X增大，S型剖面逐渐拉直，富余管线的收缩特性使得海洋柔性管道具备灵活适应复杂海底环境的优势。

图5 集矿机不同位置对应的柔性立管系统静平衡构型

图6为设置浮力块的局部管线在静平衡构型中的轴向应力。无浮力设备时，管线轴向应力自海面向下线性降低，海底富余长度的管线由于较小的轴向应力而出现局部松弛。浮力设备的施加调整了相应位置的轴向应力分布，有效改善了海底富余管路的松弛现象。紧凑的S型剖面的轴向应力呈V型分布，存在最小应力的拐点。随着S型剖面逐渐拉直，管路轴向应力呈线性增加，过渡拐点消失。

图6 不同静平衡构型中浮力施加节点处的轴向应力

6.2 柔性管道入水布放过程非线性动力学分析

第二阶段为柔性立管系统入水布放过程的动力学分析。柔性管道一端固定于水面静止的母站，另一端联接湿重8.5 t的集矿系统。释放至集矿系统着床的柔性管道系统入水过程中，构型随时间变化历程如图7所示。集矿系统自水面释放经历8.75 s接触海床面，假定集矿机接触海床面以后位置不再变化，落地位置与水面母站的水平位移为226.87 m。数值结果表明，浮力设备及海洋环境载荷对集矿系统的着床位置有显著影响。图8为集矿系统接触海床面后，柔性立管四个局部位置的节点坐标随时间变化历程。在海洋环境载荷的非保守力作用下，柔性立管动力学响应呈类周期性。

图7 柔性立管系统构型随时间变化历程

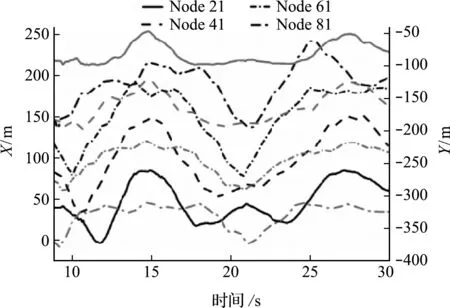
图8 局部节点位置随时间变化历程

7 结 论

本文基于三维固体有限变形理论建立全柔性立管系统的数学模型，采用非线性有限元方法得到了非保守载荷作用下几何非线性柔性立管系统的数值计算模型，开发相应计算软件应用于柔性立管系统静动力学问题的数值模拟。有限变形理论对结构位移和应变大小不做任何限制，严格考虑几何非线性因素并代入公式推导，广义α隐式时间推进格式在数值计算过程中有效处理高频段和低频段的数值阻尼，提升了数值模拟软件对非线性动力学问题的处理能力和适应性。本文软件有望处理柔性立管系统工程实际中更加复杂的非线性动力学问题。