基于物理信息的深度学习求解矩形薄板力学正反问题

唐明健， 唐和生

(同济大学 土木工程学院，上海 200092)

1 引 言

工程领域往往伴随着许多力学正反问题的分析。如已知物体的材料或介质参数，以及受力状态和边界条件等，求解其应力、应变和位移等，这种问题称为力学正问题；但有时正问题的某些条件或参数未知，需要通过获取的变形或应变等数据，反向推算得出材料参数或边界条件等情况，这种问题即为力学反问题[1-5]。这些力学正反问题都随着其本身复杂程度的增加以及已知或测量数据有限而极具挑战性。

随着计算机技术的不断发展，人工智能和机器学习等方法开始运用到解决复杂力学问题中。目前，基于数据驱动的深度学习方法应用较为广泛。如贠永峰等[6]研究建立了用于位移反分析的BP神经网络，对隧道围岩力学参数进行反演；杜其通等[7]提出一种基于神经网络的动力学参数辨识方法，并应用于机器人的模型控制系统。这种方法在一定程度上解决了一些用经典数学物理手段难以求解的问题，但是仍然存在许多不足。首先，基于数据驱动的神经网络中，待识别的网络参数仅与所提供的力学响应数据有关，通过这些数据训练最终得到的参数中所包含的力学信息比较有限；其次，这种网络一般需要合适的网格点上对应的数据或者较多的数据训练集支撑，实际采集数据时,如果限制于成本等原因，获得的数据集有限，或者得到的数据局限于某一特定区域内，对整个区域的预测结果可能无法接近真实解答。

为提高基于数据驱动的模型的可解释性和计算精度，近年来国内外的一些学者提出了基于物理信息支撑的深度神经网络[8]。如Haghighat等[9]引入平衡方程与本构关系，并应用于弹性力学问题，实现对变形的预测；Chakraborty[10]提出了一种包含多重物理信息的深度学习神经网络，可以从系统的控制微分方程中编码得到有效的物理信息；张亦知等[11]针对湍流问题，基于物理条件的约束，建立了修正模型，对湍流摩擦阻力进行预测。

本文在传统的数据驱动模型基础上，添加力学方程和本构关系等一些物理信息约束条件，在损失函数中增加相应的表征项，并以弹性矩形薄板力学正反问题为例进行分析。正问题为已知薄板基本参数、边界条件和受力状况，求解板内各点挠度大小；反问题为已知薄板基本参数、受力状况以及板内部分点的挠度，识别四条边界条件的种类。对于力学正反问题，建立深度神经网络模型，并利用基于Keras包装器的SciANN框架[12]编制深度学习的程序，对模型进行训练和预测，并与基于数据驱动的模型预测结果进行比对。

2 力学正反问题和基于物理信息的神经网络基本框架

2.1 神经网络基本框架

一般的神经网络基本框架如图1所示。

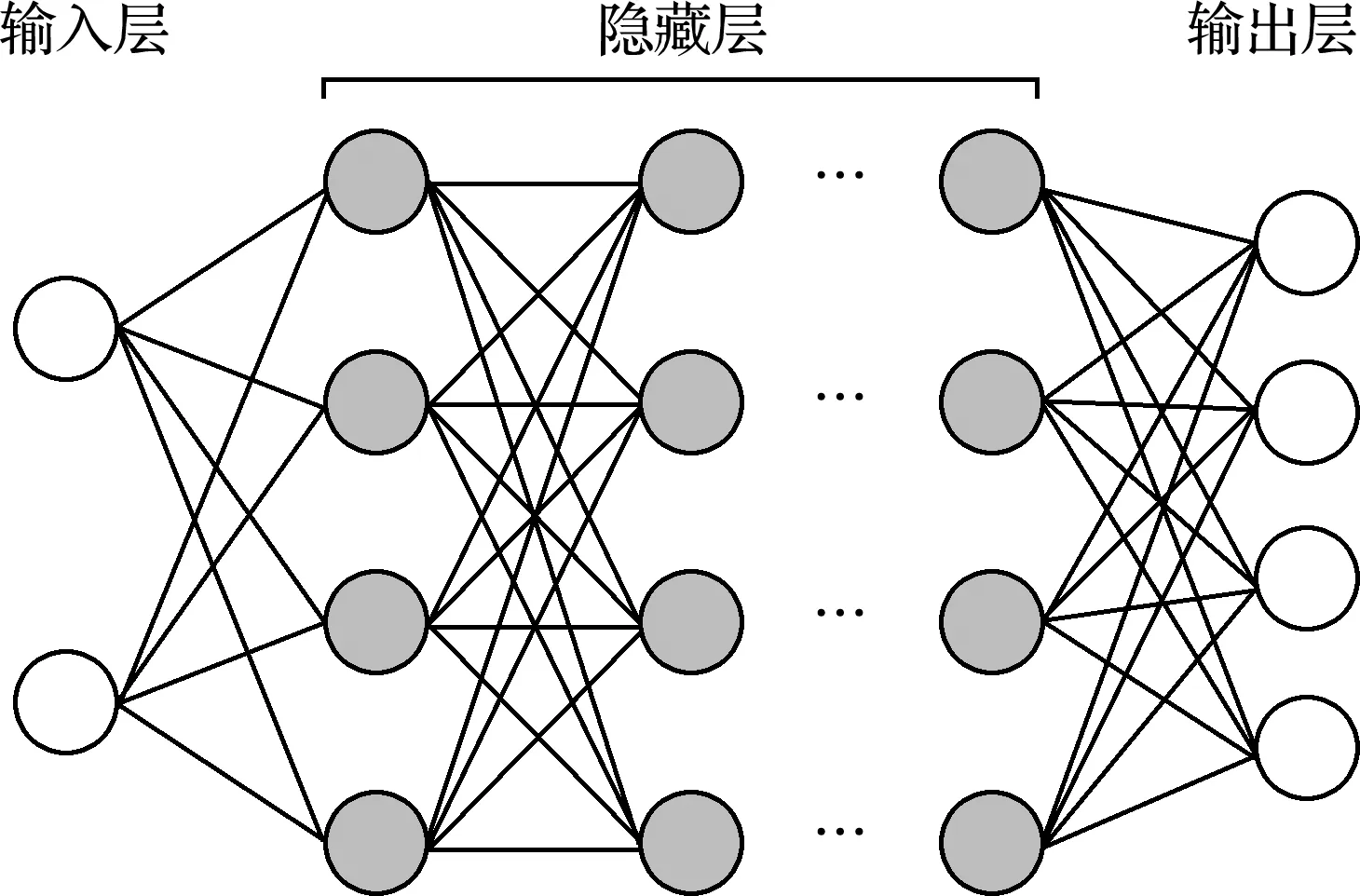
图1 神经网络基本框架

假设神经网络一共有n个隐藏层，激活函数为σ，则第i层第j个神经元的数据与前一层各神经元的映射关系可表示为

(1)

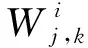
假定神经网络的输入变量为X，输出变量为Y，神经网络待识别参数θ=[W,b]，则神经网络的输入与输出层之间的映射关系可表示为

Y=N (X;θ)

(2)

式中N (·;θ)为参数θ下的神经网络算符。

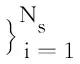
2.2 力学正问题

力学正问题中，通常已知物体的材料参数和受力情况等条件。考虑一般性的力学正问题，假设待求物体的位移为u，所受外力为F，物理参数为λ，则可以将力学问题表示为

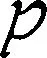
(3)

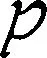
力学方程(3)通常需要合理的边界条件(4)作为定解条件,

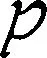
(4)

式中∂Ω为待求解物体的边界。

根据式(3，4)联立可求解未知的物体位移，进而求解其应力和应变等力学响应量。

采用深度学习的方法对力学问题进行求解时，需要确定其损失函数的表达式。考虑正问题的损失函数时，按照基于数据驱动的方法，只需要直接对物体的位移数据进行训练，让神经网络自主识别数据之间的关联。此时，损失函数可表示为

(5)

式中u*为待求解物体位移的精确值。

(6)

(7)

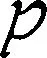
综合式(5～7)，得到力学正问题的损失函数基本可表示为

(8)

2.3 力学反问题

力学反问题中，通常已知物体的实际变形或应力和应变情况，而物理参数、受力状况和边界条件等有一项未知。假设反问题中未知条件表现为λ的若干个参数λ(1),…,λ(m )待定，该问题的损失函数仍然按照式(8)的形式，对未知参数的识别则可一般性地表示为下列最优化的问题。

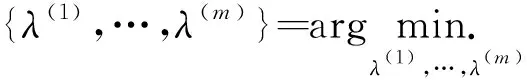
(9)

在反问题参数识别中，上述最优化问题的求解体现在迭代中对未知参数的更新。有关文献提出了许多优化算法，本文采用梯度下降算法[13]参数更新公式，对于第i个参数λ(i )，其更新表示为

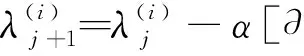
(10)

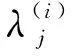
3 基于物理信息的深度学习求解矩形薄板力学正反问题

以矩形薄板受均布荷载q作用的问题为例，空间坐标系如图2所示。

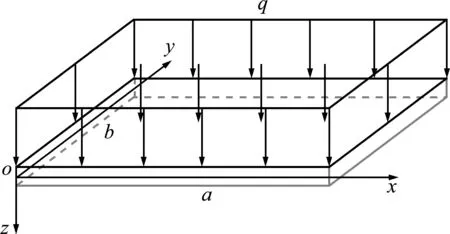
图2 矩形薄板受均布荷载作用的基本问题

基于小挠度理论和Kirchhoff假设建立的矩形薄板弯曲基本方程[14]如下，

22w/D

(11)

式中w为矩形薄板的挠度,q为作用于薄板的均布荷载大小,D为薄板的抗弯刚度，D=Eδ3/[12(1-ν2)]，E和ν分别为矩形薄板材料的弹性模量和泊松比，δ为薄板的厚度。

矩形薄板各点应变与挠度之间的关系和应力应变的本构关系为

τx y=E/[2(1+ν)]γx y

(12)

本文矩形薄板的力学正问题为,已知薄板的材料参数、四条边界条件和受力情况，求解平面坐标下各点的挠度大小w(x,y)。对于正问题，神经网络的主要输出变量即为挠度大小，但为表征尽可能多的物理信息，考虑将应力应变的本构关系引入到损失函数中。因此在正问题的神经网络输出变量中，添加σx,σy和τx y作为辅助的输出变量，并为每一个应力分量添加一个子网络，每一个子网络的输入变量均相同，且各子网络的隐藏层层数设置一致，整体神经网络框架由各子网络组合而成，共同建立输入和输出变量的映射关系。

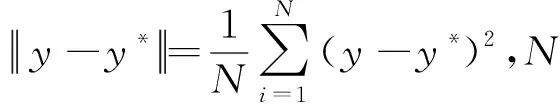
(13)

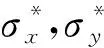
该问题的神经网络框架如图3所示。

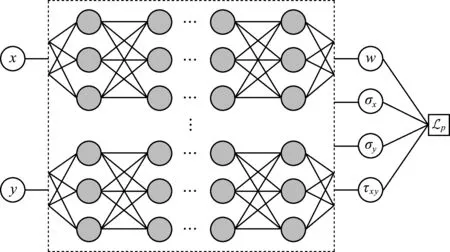
图3 矩形薄板力学正问题的神经网络框架

本文矩形薄板的力学反问题为，利用薄板内若干点的位移和薄板的基本材料参数和受力情况等已知信息，识别薄板的四条边界条件。本文以简支和固支两种边界为例进行讨论，即将边界条件的识别转化为二分类问题。为了对边界进行有效识别，引入α1,α2,α3和α4四个参数，并添加损失函数项如下，将边界条件的识别转化为四个参数的取值识别，

(14)

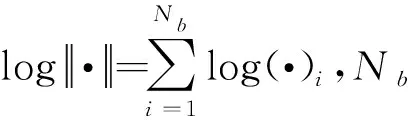
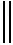
各参数识别理论取值与实际薄板边界条件对应情况如图4所示。

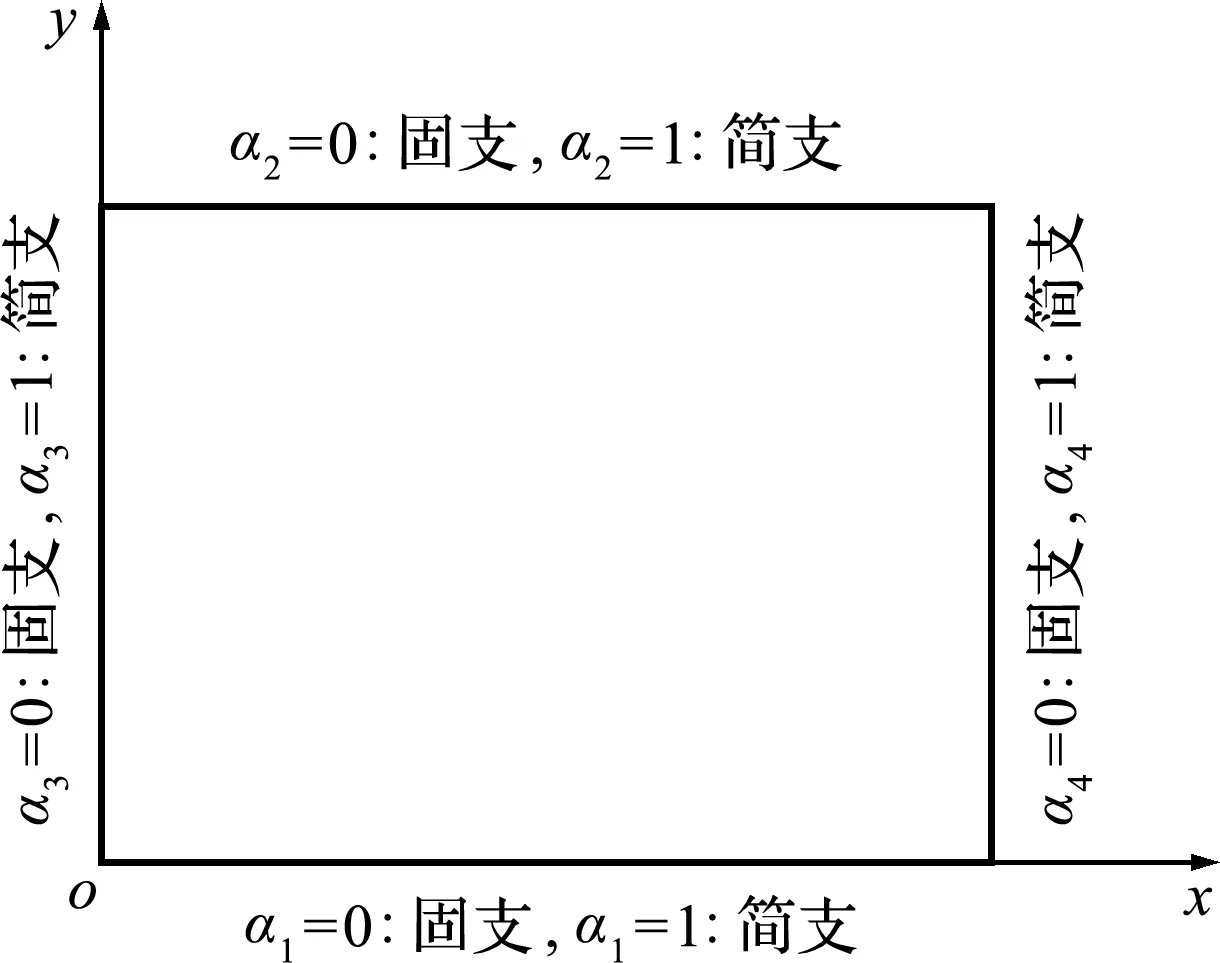
图4 各参数取值与薄板边界条件对应情况

若考虑薄板具有多种边界条件，假设第i条边界∂Ωi对应第j种边界条件，该边界需要满足的定解方程式为

(15)

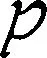
类似于式(14)，对于一般的薄板边界条件识别，假设有n种边界条件，可添加损失函数项为

(16)

对于式(16)参数的取值,讨论方法与前面基本相同。因此,力学反问题的损失函数可表示为正问题式(13)和边界识别项式(16)之和。

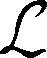
(17)

该问题的神经网络框架与正问题类似，挠度和应力分量同样采用子网络。讨论固支和简支两种边界条件下，在原来的基础上添加对四个参数的识别。网络框架如 图5 所示。

在矩形薄板力学正问题和反问题计算损失函数时，都涉及到对挠度数据进行高阶微分，如果采用一般的数值差分方法，其误差较大，且高阶的数值微分需要划分足够多的结点来保证计算精度，因此本文采用自动微分[15]的计算方法，可以在机器学习过程中大大降低计算代价，且计算精度不会明显地受到网格点数的限制。计算时采用正向微分形式，可以通过一些目前已有的前馈神经网络模型[16，17]加以实现。

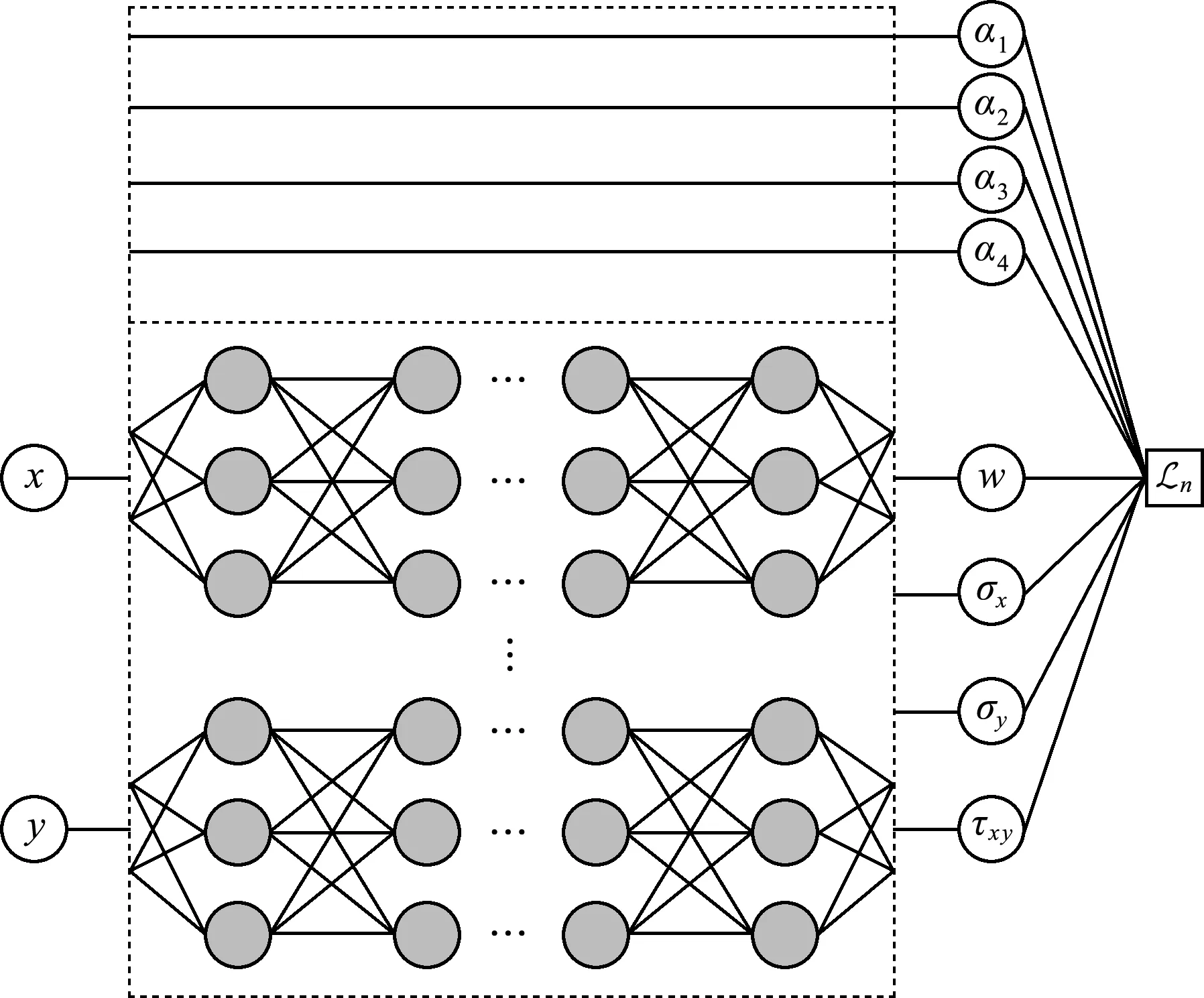
图5 矩形薄板力学反问题的神经网络框架

4 算例分析

4.1 矩形薄板力学正问题

矩形薄板力学正问题采用四边简支矩形薄板问题，其挠度可用双重三角级数表示[14]。选取参数E=1000，ν=0.25，q=1000,a=b=1，薄板厚度取单位尺寸。

进行模型的预测之前，首先对各种不同的神经网络拓扑结构迭代收敛效果进行了测试。训练数据集为薄板上均匀划分网格点20×20上的挠度和应力数据，单次训练选取的样本数取为32，选取六种不同的神经网络隐藏层结构分别为,① 3层各20个结点；② 5层各20个结点；③ 3层各40个结点；④ 5层各40个结点；⑤ 3层各80个结点；⑥ 5层各80个结点。针对不同的网络拓扑结构，利用数据集进行模型训练，并设置当损失函数取值在500次迭代中都没有下降时停止训练，输出结果。

对六种不同的网络隐藏层拓扑结构训练，模型迭代收敛曲线如图6所示。可以看出，当层数增加的时候，虽然最终预测的合理性偏向于更加准确，但是训练过程中振荡加剧。文献[9]提出，当设置的神经网络层数过多，容易导致训练过程中出现过拟合，因此实际选取神经网络层数时应当加以控制。横向对比相同层数不同结点数下的计算结果，当计算结果接近收敛时，神经网络隐藏层结点数较多的模型的最终预测效果较好。综合考虑模型训练速度、收敛曲线振荡情况和预测效果，最终选择隐藏层为三层各40个结点的神经网络作为该问题的网络拓扑结构。

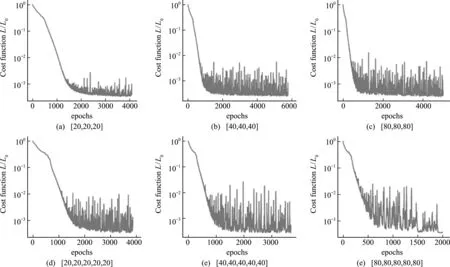
图6 不同网络结构下模型迭代收敛曲线(四边简支板)

利用均匀划分网格20×20的模型训练并预测整个矩形薄板上各点挠度，并与精确计算值比较，结果如图7所示，可以看出模型的预测效果良好。

图7 薄板挠度预测与精确计算结果对比(四边简支板)

实际工程中，减少矩形薄板挠度数据的采集点数的同时保证计算精度，对于节省测量成本和加快训练时间等具有非常重要的意义。为此，对不同网格点数划分下的模型分别进行了训练，图8展示了均匀网格划分6×6和10×10下的模型预测结果。结果显示，当网格划分接近10×10左右时，计算精度已经达到要求，相应的损失函数收敛速度也与20×20的网格点数基本无异，说明实际取10×10左右的均匀网格划分已经可以满足计算要求。

图8 不同网格结点数下预测结果对比(四边简支板)

为了进一步说明基于物理信息的神经网络模型的计算效果，对基于数据驱动和基于物理信息的模型训练与预测结果进行对比。计算结果显示，在相同网格点数下，当已知挠度数据均匀分布在整个薄板区域内时，在相同迭代次数下，二者的预测精度没有非常显著的区别，这可能是因为基于数据驱动的模型网络参数较少，容易收敛，而基于物理力学信息的模型迭代收敛较慢。在网格点数均取为10×10的计算结果中，基于数据驱动的模型在初始训练迭代约1200次就基本收敛，而基于物理信息的模型需要迭代2500次左右。

但是，当所得到的挠度数据局限于薄板某一区域内时，虽然在已知数据的区域一侧二者预测精度没有明显的区别，但是在对未知区域的挠度进行预测时，基于数据驱动的神经网络的预测精度明显低于考虑了物理信息的模型。本文选取了薄板的左半边区域[0,0]×[1/2,1]内的10×10挠度数据进行训练，两种网络模型的预测结果如图9所示。

图9 两种神经网络模型训练预测结果对比(四边简支板)

4.2 矩形薄板力学反问题

本文以相邻两边简支其余边固支，受均布荷载作用的矩形薄板问题作为矩形薄板力学反问题的计算实例。对于该问题的精确解答，根据文献[18]提出的叠加法计算思想，可以求解出各点挠度数据，进而得到应力和应变。

选取与4.1节相同的基本物理参数，取薄板两条固定边为x=0和y=0，并在均匀划分网格 20×20的情况下，选取了六种不同的神经网络隐藏层拓扑结构，进行了收敛速度和学习效果的测试。考虑到反问题的边界条件和挠度分布等比较复杂，选择采用稍深层的网络进行测试，分别为 ① 4层各20个结点；② 6层各20个结点；③ 4层各40个结点；④ 6层各40个结点；⑤ 4层各80个结点；⑥ 6层各80个结点。对六种不同的网络隐藏层拓扑结构训练，模型迭代收敛曲线如图10所示。

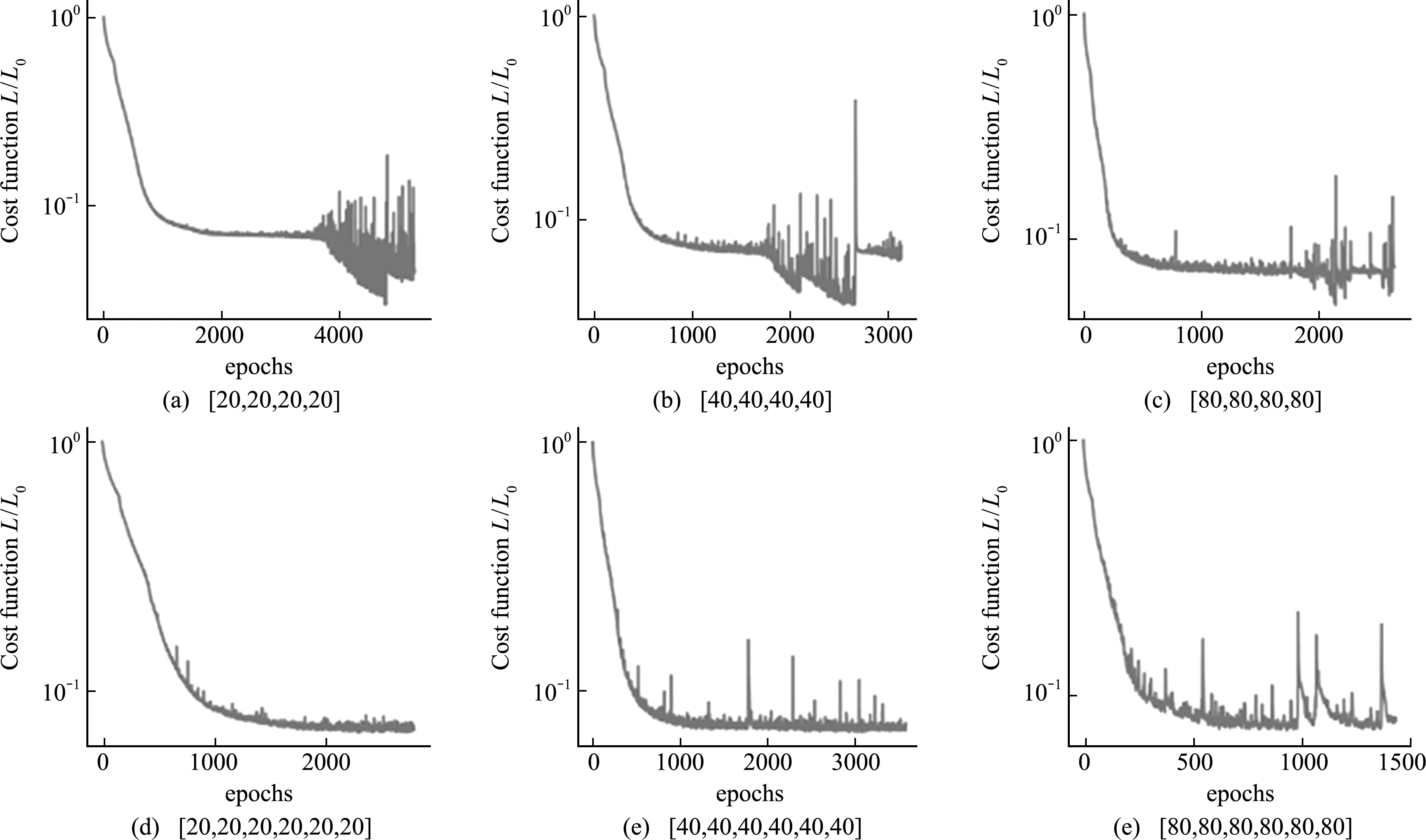
图10 不同网络结构下模型迭代收敛曲线(两边固支两边简支板)

经过收敛情况和计算结果的综合比对，最终选择神经网络隐藏层为六层各20个结点的网络模型，其收敛情况较好，且模型预测精度较高。

设定四个边界参数的初始值均为0.5，利用 20×20的模型训练并预测矩形薄板各点挠度和四条边界条件，与精确计算结果对比如图11和表1所示，可以看出，整体而言该模型的预测效果较好。

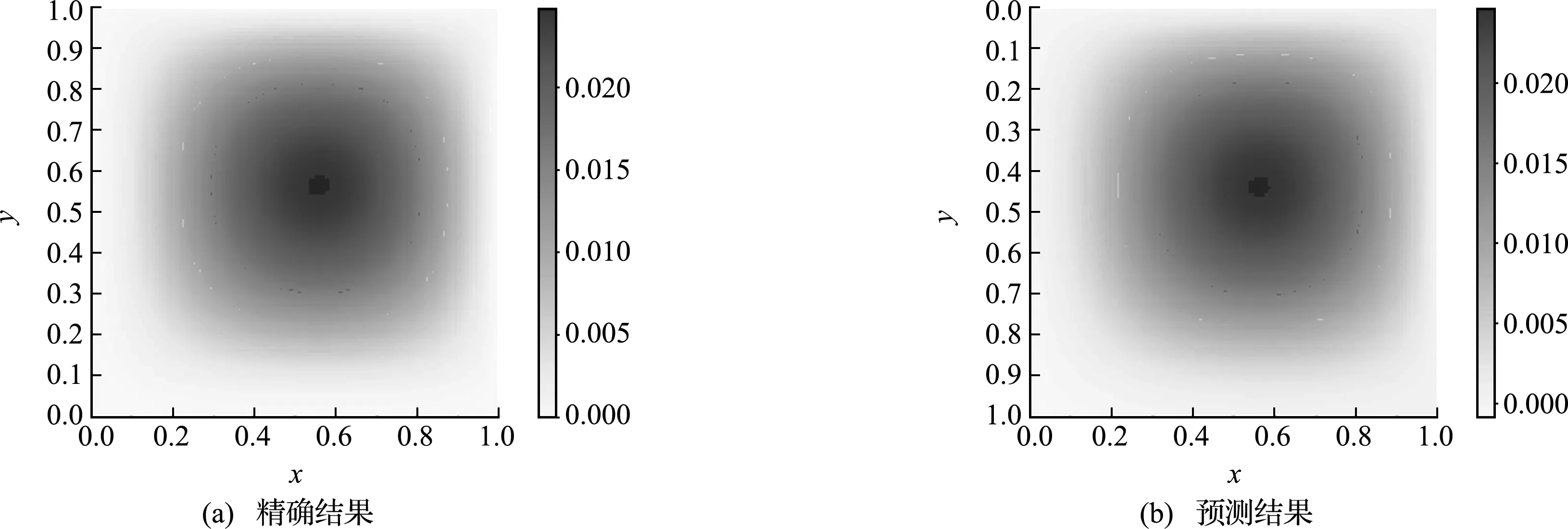
图11 薄板挠度预测与精确计算结果对比(两边固支两边简支板)

反问题中，同样对不同网格点数划分下的模型分别进行了训练，图12展示了均匀划分网格8×8和14×14下模型的预测结果。结果显示，当网格划分接近14×14左右时，整个薄板区域内的计算精度基本满足要求。

图12 不同网格结点数下预测结果对比图(两边固支两边简支板)

对力学反问题计算中对基于数据驱动和基于物理信息的模型训练与预测结果进行比较。计算结果同样表明，当所选数据局限于某一区域内，对未知区域内的薄板挠度进行预测时，基于物理信息的模型预测精度远高于基于数据驱动的模型。本文选取薄板左上角区域[1/2,1/2]×[1,1]内的14×14挠度数据进行训练，计算结果如图13所示。

图13 两种神经网络模型训练预测结果对比(两边固支两边简支板)

结果表明，基于物理信息的模型除在两固支边交界的位置预测精度受到较大影响，其余位置仍保持了较高的预测精度，而基于数据驱动的模型不仅在其他点上的挠度预测与实际值偏差非常大，同时在训练过程中发现，基于数据驱动的模型迭代收敛的情况更容易受到所提供薄板挠度数据集的影响，当数据集不充分，模型难以收敛到正确的结果。

5 结 论

基于物理信息的深度神经网络，在原来依靠数据驱动的网络模型基础上，于损失函数中引入表征力学位移、应力和应变等之间的关系，使得在模型训练过程中神经网络的参数具备相应的力学特征。本文以矩形薄板的力学正反问题为例，正问题为已知矩形薄板的基本参数与受力情况求薄板各点挠度，损失函数添加了挠度基本方程和应力应变本构关系等项；反问题为已知矩形薄板挠度和基本参数求四条边界条件，在考虑简支和固支两种边界条件时，将四个边界条件的确定转化为四个0～1参数的识别，并在损失函数中添加相应的表征项，通过模型训练确定边界条件。以四边简支矩形薄板和相邻两边简支其余边固支矩形薄板为算例进行测试，根据收敛情况和预测精度选取了神经网络的拓扑结构，并将预测的矩形薄板挠度和边界条件表示出来。结果显示，基于物理信息的神经网络不仅对未知点挠度和边界条件的预测效果很好，而且在已知局部区域推算整个矩形截面的挠度问题上，其计算精度远高于基于数据驱动的模型，因而在力学和工程领域更具备使用和推广的价值。